基于小波去噪的阈值函数改进方法分析①

田江龙 屈卫东

(上海交通大学电子信息与电气工程学院)

基于小波去噪的阈值函数改进方法分析①

田江龙 屈卫东

(上海交通大学电子信息与电气工程学院)

首先介绍了两种国内外比较有代表性的小波阈值改进方法，并在传统软、硬阈值函数的基础上提出了一种新的改进阈值函数，通过对小波系数的阈值处理，使得去噪后的信号在过分平滑与边缘振荡现象之间达到合理的平衡。对一段压气机台架实验数据的仿真分析表明：该方法在去噪的同时减少了有用信息的损失，在信噪比增益和最小均方差误差方面的性能指标要优于传统软、硬阈值法，同时在3种改进阈值函数方法中具有最佳的去噪性能。

小波去噪 软阈值函数 硬阈值函数

信号去噪问题一直是一个重要而且热门的课题。近些年来，随着小波分析理论的日臻完善和小波研究的不断深入，小波分析的应用日趋广泛。其中，利用小波分析进行信号去噪是信号处理领域的重要应用之一，并且已经显示出比传统的傅里叶分析更多的优势。目前，小波去噪方法大致分为3类：基于小波变换模极大值原理的小波去噪、基于相邻尺度小波系数相关性的小波去噪和小波阈值函数去噪。阈值函数法是Donoho D L在1995年提出的一种简单有效的小波去噪方法[1]，由于该方法在Besov空间上可得到最佳的估计值，是其他线性估计方法所达不到的，因此引起了国内外学者的广泛关注与研究。但是，该方法采用的软阈值与硬阈值函数仍存在一些有待改进的地方，如硬阈值函数由于不连续会使得信号在突变处出现振荡现象；软阈值函数会损失有用的高频信息，去噪后信号过于平滑等。针对这些问题，国内外的很多学者提出了一些解决方案和改进方法[2,3]，如最大似然估计法、软硬阈值折衷法、多项式插值法及修正软阈值法等，并进行了大量的实验验证，从而进一步提高了小波阈值去噪法的去噪性能，扩展了其应用领域。

笔者首先介绍小波阈值去噪的原理和传统的软、硬阈值函数，然后在传统阈值函数的基础上提出了一种新的小波阈值函数，并进行了理论分析与仿真验证。然后选取3种国内外有代表性的改进方法和笔者的改进方法对截取的一段压气机台架实验数据进行去噪分析，并对比了它们的去噪性能。

1 小波阈值函数去噪法

1.1 小波阈值函数去噪原理

假设一维含噪声信号的数学模型为[4]：

f(k)=s(k)+n(k)

(1)

其中，f(k)为含噪声信号，s(k)为原始信号，n(k)为均方差为σ2的高斯白噪声，服从N(0,σ2)的标准正态分布。则通过小波阈值去噪法从f(k)含噪信号中得到s(k)的过程可分为以下3个步骤：

a. 利用小波对含噪信号进行分解。选择小波分解层数N和合适的小波包，对含噪声信号f(k)进行N层小波分解，获取各尺度小波系数ψjk。

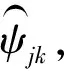
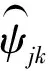
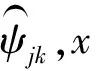
1.2 传统阈值函数

小波阈值去噪方法的焦点在于对高频小波系数的估计，传统的阈值函数有软阈值和硬阈值函数两种。

传统硬阈值函数的数学表达式为：

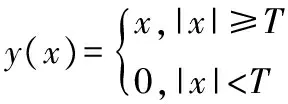
(2)

传统软阈值函数的数学表达式为：

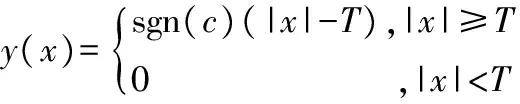
(3)

硬阈值函数是将绝对值小于阈值的小波系数设为零，而将绝对值较大的系数全部保留，由于该函数是不连续的，小波重构后所得到的信号会出现振荡。软阈值函数则是将绝对值较大的系数减去固定值T，这样会直接影响重构后的小波信号与原始信号的逼近程度，造成较多的高频信息损失，导致信号的边缘模糊。在实际工程应用中，通过软阈值函数法去噪后的信号较光滑，有着较大的信号失真，而利用硬阈值函数去噪后的效果并不理想，且对时变信号的去噪效果不佳。

2 对小波阈值函数的改进方法

由上述分析结果可见，传统的软、硬阈值函数还存在一些不足之处。国内外在这方面已做了大量研究，并提出了一些改进函数。笔者选取两种比较有代表性的改进方法进行介绍并做理论分析，然后在传统软、硬阈值函数的基础上提出一种新的阈值函数方法。为了叙述方便，笔者将提到的3种改进方法分别称为：改进方法一、改进方法二和改进方法三。

2.1 改进方法一

改进方法一是一种改进硬阈值法[5]，其表达式为：

(4)

其中，n为任意正常数，即n∈Z,当n→+∞时阈值函数等效于软阈值函数，当n→0时阈值函数等效于硬阈值函数。通过调整n的值，使得该函数在软、硬阈值函数之间变动，从而获得不同的去噪性能。改进方法一(在n=0.5,T=3时的函数如图1所示)是对硬阈值函数的一种改进方法，使得阈值处理时在阈值T处的小波系数能平滑过渡，从而使得去噪后的信号具有更好的连续性。

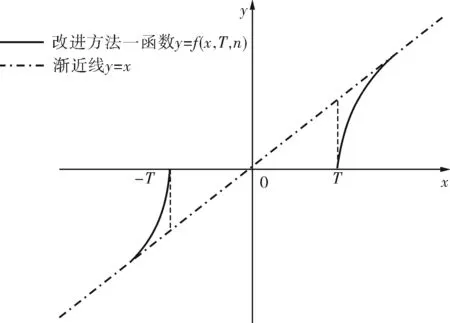
图1 改进方法一函数示意图

2.2 改进方法二

改进方法二是一种双变量小波阈值函数[6]，其表达式为：

(5)

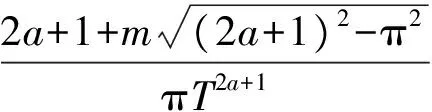
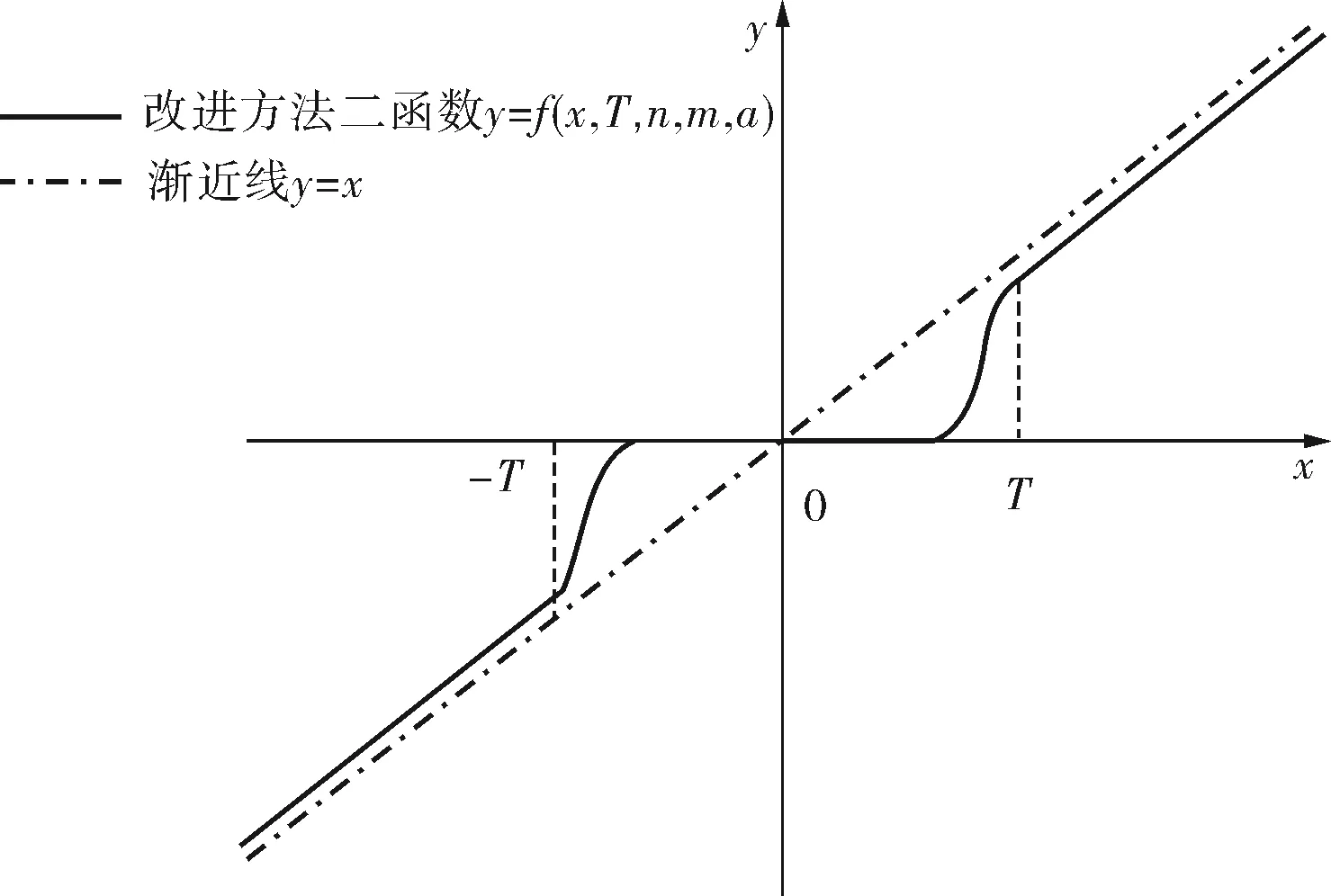
图2 改进方法二函数示意图

2.3 改进方法三

改进方法三是笔者在对传统的软、硬阈值函数和国内外相关阈值函数研究基础上提出的一种新的阈值函数，其表达式为：

(6)

其中，a>0.5,k>0，且a、k满足如下条件：

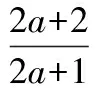
(7)

其中a是可变参数。改进方法三在有用信号和噪声信号之间形成一段连续的平滑过渡带。a参数的值用于指定过渡带的曲线阶次，a越大，过渡带曲线越陡，a越小，过渡带曲线越缓。因此，可以通过设置a来调节去噪信号的平滑度。式(7)用于保证阈值T的位置处在阈值函数二阶导数为零处，从而使得在过渡带斜率保持持续增加，使得阈值函数的曲线更快地逼近渐近线y(x)=x，从而尽量保持高频信息不损失。当参数a、T被指定，可通过式(7)计算出k。通过分析可以发现，在x=T点处的左右导数值存在如下关系：

(8)

保持a=-0.5时该阈值函数的曲线与软阈值函数的一样。当a→+∞时该阈值函数的曲线与硬阈值函数的一样。改进方法三在合理地选取参数后既有改进软阈值函数法的优点，又有改进硬阈值函数法的优点，通过文献[6]可以知道在信噪比特性方面，改进硬阈值方法的性能较一般的改进软阈值函数法要好。改进方法三在a=3,T=3时的阈值函数如图3所示。

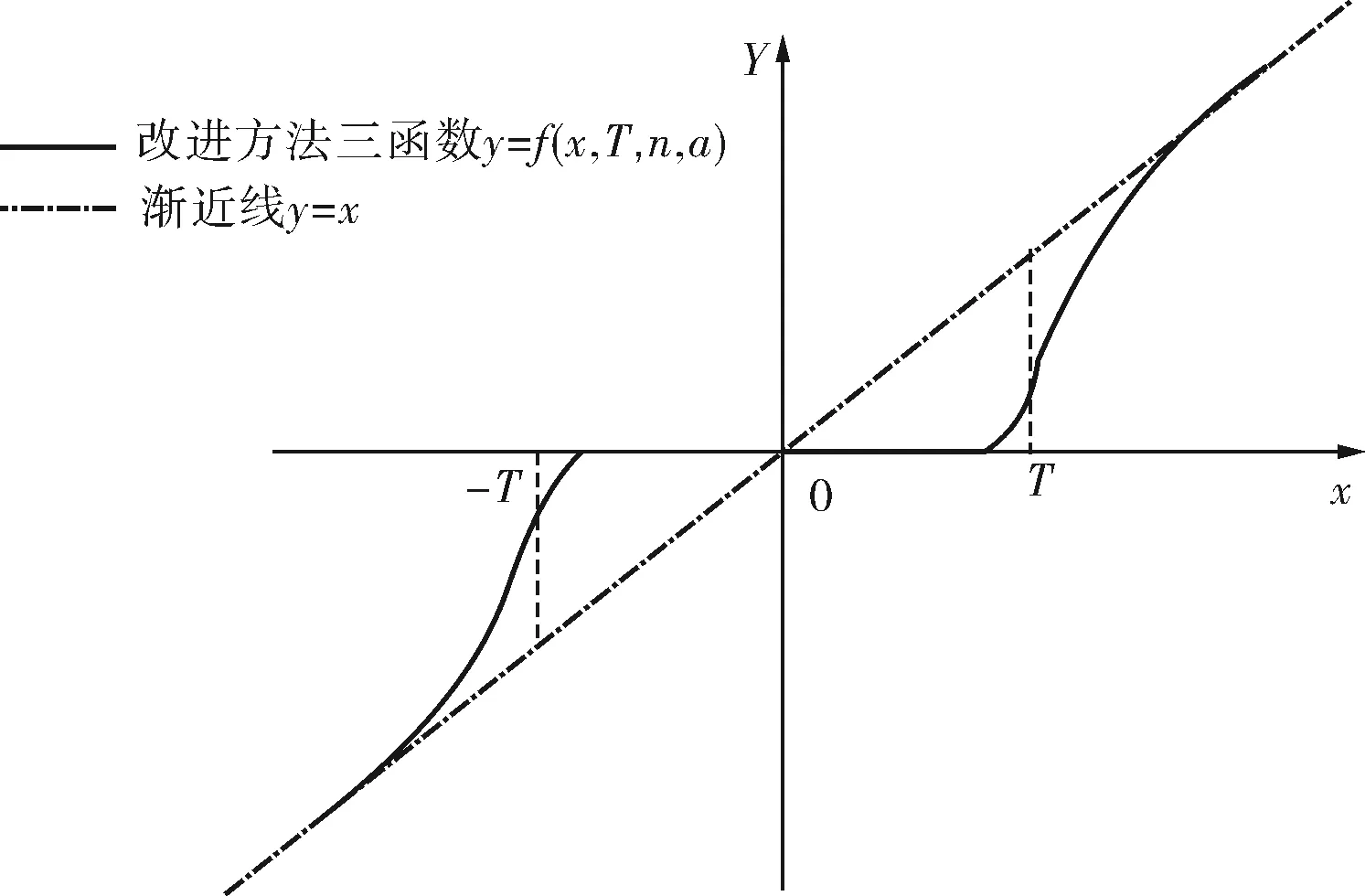
图3 改进方法三函数示意图

为了更为直观地显示参数a对阈值函数的影响，分别取a=-0.5,a=0.5,a=3,a=200绘制函数曲线(图4)，由图可见阈值函数变换趋势与理论分析相符。

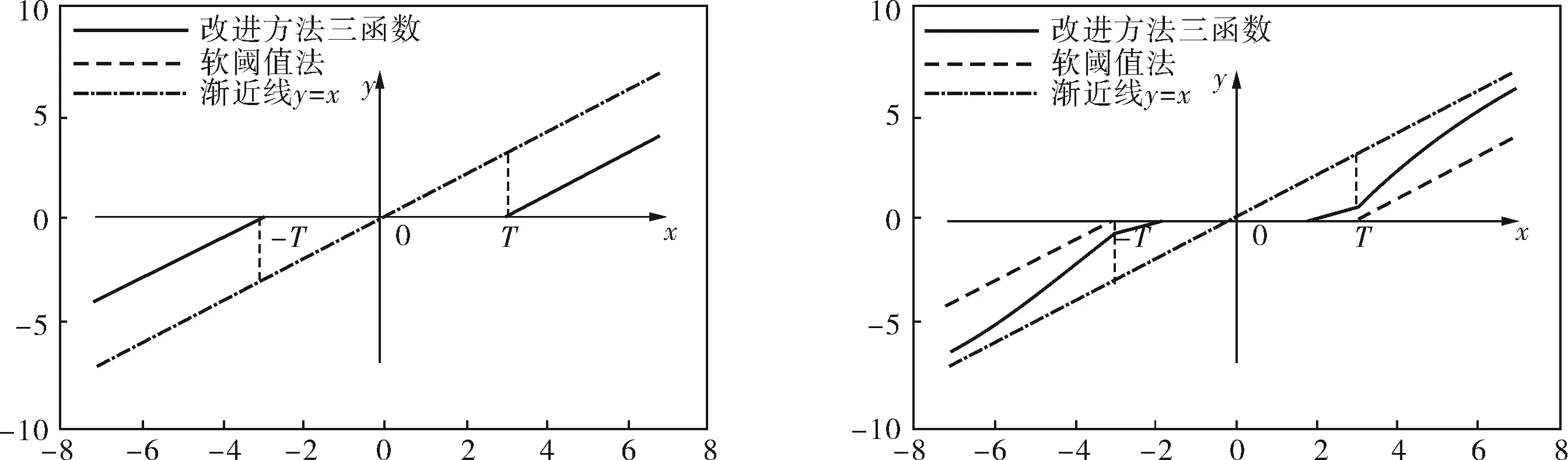
a. a=-0.5 b. a=0.5

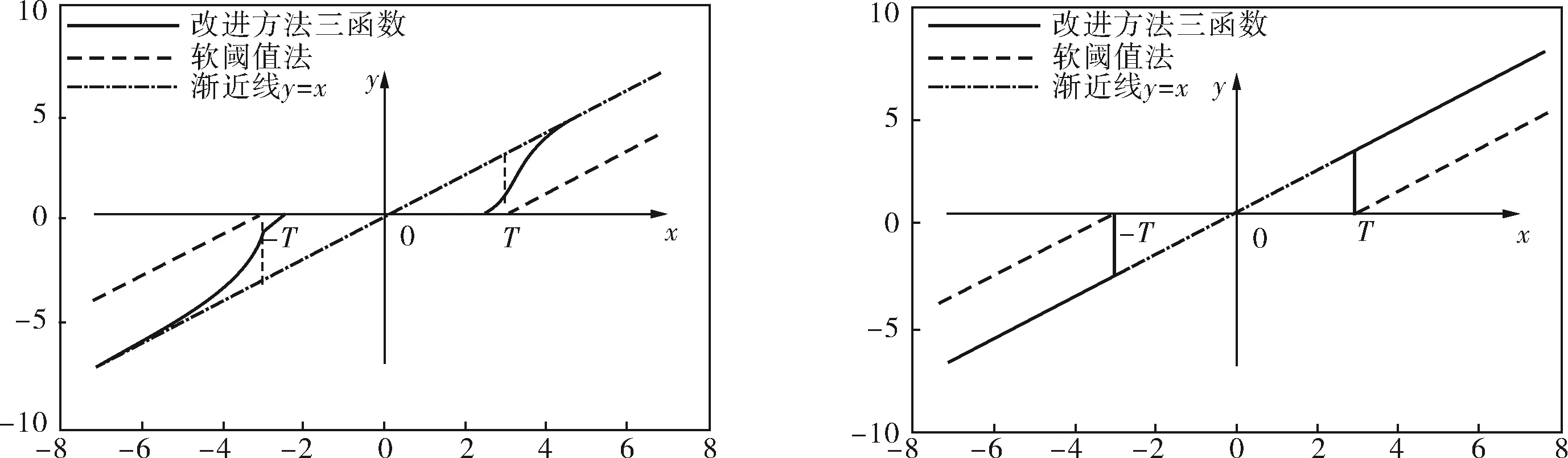
c. a=3 d. a=200

3 去噪性能对比分析

为了能够获得笔者所介绍的3种改进阈值函数在小波阈值去噪中的性能特性，分别采用软、硬阈值函数和文中所提到的3种改进阈值函数对一段压气机台架实验的静压数据进行去噪分析，并利用信噪比SNR和均方差误差RMSE这两个性能指标对降噪效果进行量化，以便进行比较。

选择db8小波对所选实验数据进行5层小波分解，并对小波系数分层(即d1～d5共5层)后的数据设置阈值T。通过前面章节的分析可知，小波阈值T在去噪过程中起着至关重要的作用。若阈值T设置太大，将会丢失较多有用的高频信息，从而造成小波重构后的信号存在较大的失真；而如果阈值T设置太小，那么阈值函数处理后的小波估计系数中依旧含有很多噪声分量，与去噪的初衷不合。文中阈值T通过统一全局阈值法[7]求取，它在实际的工程应用中具有较好的效果，其数学表达式如下：

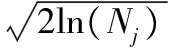
(9)

其中，Nj为j尺度上的小波系数的数据长度；σj=MAD(|ψjk|)/q,MAD(·)表示对数据取中值，q是常数，根据经验取0.4～1.0之间的值，笔者选择q=0.7。笔者对压气机实验室数据进行仿真计算得到各层小波系数的阈值设置见表1。

表1 各层阈值设置

由上述分析可知，所选的3种改进阈值函数均有可变参数，且其去噪效果与参数值有关。因此，通过参考各文献的参数设置和Matlab仿真结果，各改进函数参数取值分别为n=0.2,m=0.9,a=3和a=3时得到的均方差最小，信噪比最大。5种阈值函数的去噪性能对比见表2。

表2 5种阈值函数的去噪性能对比

从表2的对比结果可见，硬阈值函数法要比软阈值函数法的去噪性能好，原因在于软阈值函数去噪后信号尽管比硬阈值函数法平滑，但损失了更多的高频成分。改进方法一是一种改进的硬阈值函数，实验结果表明此方法去噪性能要比传统硬阈值函数法优越。改进方法二是一种改进的软阈值函数，实验结果表明其去噪性能要比传统软阈值函数优越，但是其平滑作用也损失了较多有用高频信号，使得其性能并不优于改进方法一。笔者提出的改进方法三在5种函数方法中去噪性能最佳，去噪后信号的信噪比提升最多，均方差误差系数最小。当然，表2的对比结果与各层小波系数阈值的选取也有一定关系，通过改变阈值的取值发现，随着阈值增大，这5种方法的信噪比趋于同一个值，随着阈值减小，信噪比均有不同程度的增大，但大量实验结果表明，笔者所提的方法均有最佳的表现。选取信噪比最大的两种方法的去噪后信号与原始信号的对比如图5所示。

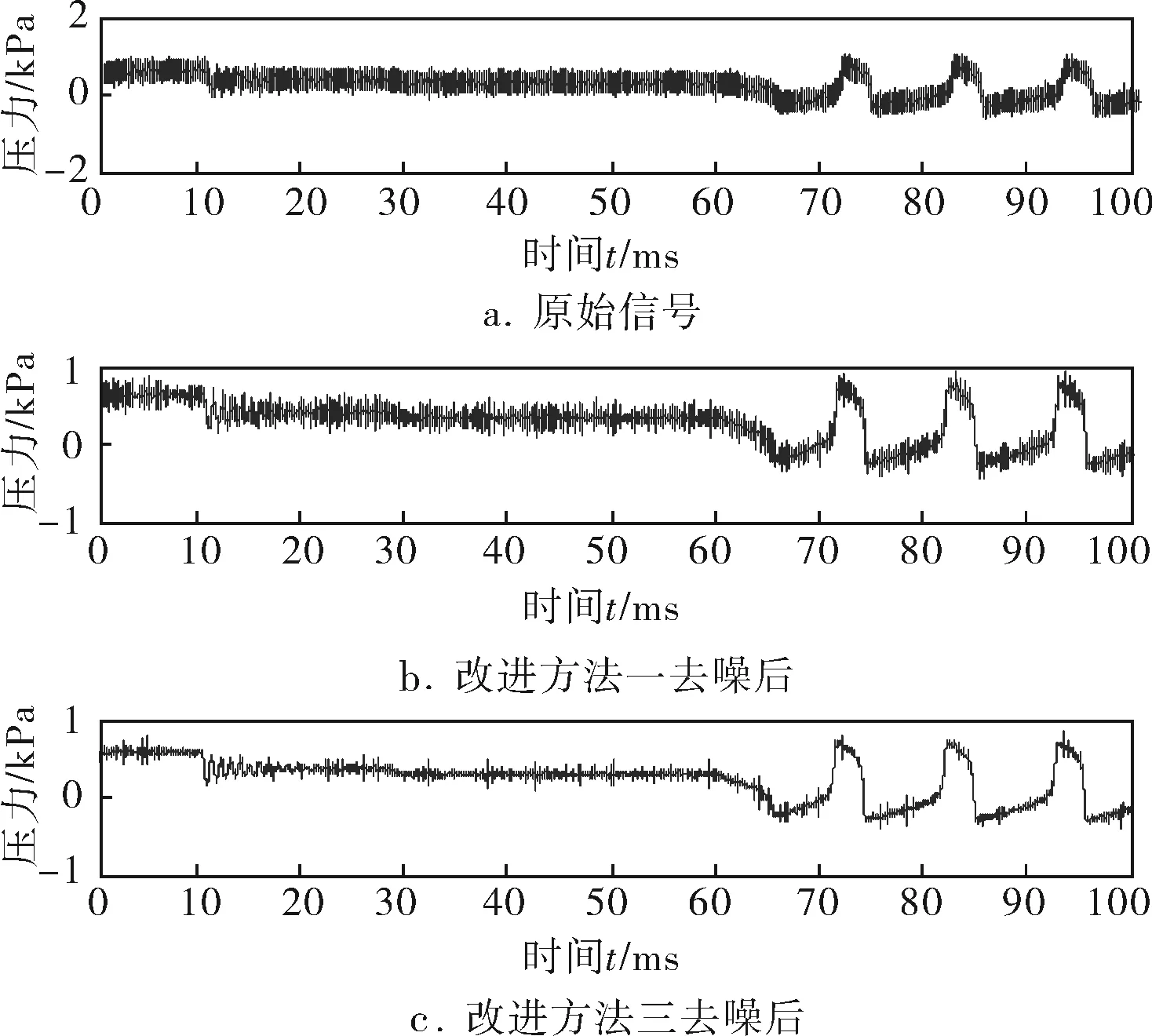
图5 改进方法一、三去噪结果对比

通过以上分析，分析结果与各方法的理论分析结果相符，笔者所提出的去噪方法较其他几种方法具有明显的优越性。

4 结束语

首先通过介绍小波阈值去噪的原理，然后针对传统小波软、硬阈值函数存在的不足介绍了3种改进的阈值函数，并通过Matlab仿真实验对比分析了3种改进阈值函数的去噪性能。分析结果表明改进阈值函数在SNR和RMSE性能方面要优于传统的软、硬阈值函数。

笔者提出的新的阈值函数在3种改进阈值函数方法中去噪性能更好，且在除阈值T处外具有一阶连续导数和二阶连续导数，使它具有更好的数学特性和灵活性，更加符合自然信号的特性。因此，它既具备比传统的阈值函数更好的去噪性能，又具有阈值自适应的特性，这为信号的小波阈值去噪提供了新的可选阈值函数。

[1] Donoho D L.De-noising by Soft-thresholding[J].IEEE Trans on Information Theory，1995，41(3)：613～627.

[2] 曲天书,戴逸松,王树勋，等.基于SURE无偏估计的自适应小波阈值去噪[J].电子学报,2002,30(2):266～268.

[3] 王宏强,尚春阳,高瑞鹏，等.基于小波系数变换的小波阈值去噪算法改进[J].振动与冲击,2011,30(10):165～168.

[4] 姚建红,林娜,付强，等.基于多目标函数的粒子群算法优化小波阈值的去噪方法研究[J].化工自动化及仪表,2013,40(2):154～157.

[5] 张维强,宋国乡.基于一种新的阈值函数的小波域信号去噪[J].西安电子科技大学学报(自然科学版),2004,31(2):296～299,303.

[6] 张淑清,师荣艳,董玉兰，等.双变量小波阈值去噪和改进混沌预测模型在短期电力负荷预测中的应用[J].中国电机工程学报,2015,35(22):5723～5730.

[7] 崔蕾,张玉林,伍海龙，等.扫描电化学显微镜扫描图像处理的实现[J].化工自动化及仪表,2006,33(4):33～36.

AnalysisofModifiedMethodforThresholdFunctionsBasedonWaveletDe-noising

TIAN Jiang-long, QU Wei-dong

(SchoolofElectronicInformationandElectricalEngineering,ShanghaiJiaotongUniversity)

Two typical methods for modifying wavelet threshold functions were introduced, and basing on traditional soft and hard threshold functions, a new modified threshold function was proposed. Through the threshold processing of wavelet coefficients, the signals de-noised reached the balance between excessive smoothness and edge oscillations. Simulating experiment data from a compressor bench shows that this method can reduce the loss of useful information while de-noising the signals, and the performance index is superior to traditional soft and hard in SNR gain and in the minimum mean square error, and it has the best de-noising performance of three modified threshold methods.

wavelet de-noising, threshold function, hard threshold de-noising

田江龙(1990-),硕士研究生，主要从事高负荷轴流压气机不稳定信号的研究。

TN911.4

A

1000-3932(2017)03-0243-05

联系人屈卫东(1961-)，副教授，主要从事航空发动机控制系统与故障诊断的研究，wdqu@sjtu.edu.cn。

2016-10-17，

2017-01-22)