基于天气预报的漳河灌区参考作物腾发量预报方法比较

刘 梦，罗玉峰※，汪文超，何 军,2，崔远来



基于天气预报的漳河灌区参考作物腾发量预报方法比较

刘 梦1，罗玉峰1※，汪文超1，何 军1,2，崔远来1

（1. 武汉大学水资源与水电工程科学国家重点实验室，武汉 430072；2. 三峡大学水利与环境学院，宜昌 443002）

为了提出适合湖北省漳河灌区的参考作物腾发量预报方法，以FAO56-Penman-Monteith公式采用历史气象数据计算出的值为基准，利用天气预报数据，比较Hargreaves-Samani（HS）法、逐日均值修正法及该文改进的逐日均值修正法在该灌区钟祥站点的预报精度，并评价各方法适用性。结果表明：利用这3种方法进行参考作物腾发量预报时，1～7 d预见期平均绝对误差均值分别为0.75、0.80、0.76 mm/d，均方根误差分别为1.00、1.07、1.05 mm/d，相关系数分别为0.82、0.80、0.80。1 d预见期最优预报方法为改进逐日均值修正法，2～7 d预见期的最优方法均为HS法。总体而言，预报精度最好的为HS法、改进逐日均值修正法次之、逐日均值修正法最差。对于漳河灌区，建议采用HS法进行预报，可为灌溉预报提供较为准确的数据基础。

腾发量；天气预报；温度；Hargreaves-Samani；逐日均值修正法

0 引 言

农业用水为中国用水大户，其中满足作物需水量的部分是农业用水的主要部分[1-3]。作物需水量可以表示为参考作物腾发量（reference crop evapotranspiration, ET0）与作物系数的乘积[4]。因此精确和及时的ET0预报，对于提高实时灌溉预报精度、灌溉管理水平以及节约水资源具有重要意义[5-8]。

目前ET0预报方法分为2类，即直接法和间接法[9]。直接法即历史时间序列分析法，国内外关于ET0的预报研究多为直接法，如：Mao等[10-11]通过分析历史数据，提出了逐日均值修正模型；Mohan等[12]采用指数平滑法和自回归积分滑动平均模型（autoregressive integrated moving average, ARIMA）预测每周ET0；蔡学良等[13]对逐日均值修正模型中的经验参数进行了分析，给出了更合理的取值方法。随着天气预报精度的提高，以气象预报数据和预报模型为基础的间接法受到广泛关注，如：蔡甲冰等[14-16]使用改良的Penman- Monteith（PM）公式预报ET0；罗玉峰等[17-18]将气温预报数据输入率定好的Hargreaves-Samani（HS）公式中，进行ET0的预报。以上提到的预报方法中，由于逐日均值修正法和HS法所需的气象预报数据较少，计算公式简单，且容易嵌入灌溉预报系统，应用较为广泛[19-21]。目前关于ET0预报的研究很多，关于漳河灌区ET0的预报较少。李远华等[22]计算出了漳河灌区天气类型修正系数，并将其带入逐日均值修正法中进行ET0预报；顾世祥等[23]对逐日均值修正法中的天气类型修正系数计算方法进行了改进。但是，关于漳河灌区的研究大多采用的是逐日均值修正法，方法单一。

综上，本文选取应用广泛的HS法、逐日均值修正法，并对逐日均值修正法进行改进，比较3种不同方法进行ET0预报的精度，以期得出适用于漳河灌区的最优的ET0预报方法，为灌区ET0和灌溉预报提供依据。

1 材料与方法

1.1 研究区概况

漳河灌区位于湖北省中部、长江支流沮漳河东支的漳河上，灌区包含钟祥、当阳、荆州、荆门4个县市，面积5 543.93 km2，现有耕地面积163 167 hm2。灌区内钟祥与荆州站历史气象资料完整，而当阳与荆门数据缺失，因此本文选取钟祥站为典型站点。表1为灌区各区域的具体水文气象要素特征值，以钟祥的特征值为基准，其他地区年日照时数、年均气温、年降水量偏差分别为–2.7%～7.7%，–1.2%～1.2%，–3.7%～23.4%。各地区年日照时数、年均气温均十分接近；年降水量中，只有荆州偏差略大，当阳、荆门的偏差为2.1%、–3.7%；总体而言，灌区各区域水文气象条件相似。图1为漳河灌区示意图，其中，钟祥位于灌区北部，荆州位于灌区南部。

图1 漳河灌区示意图

表1 漳河灌区各站点的水文气象基本特征

1.2 数据来源

由中国气象数据网（http://data.cma.gov.cn）收集了钟祥站点1999年1月1日—2014年5月24日的历史气象资料。历史气象资料包含了历史逐日的平均气温、日最高气温、日最低气温、日照时数、平均风速、平均相对湿度。由中国天气网（http://www.weather.com.cn）收集了钟祥站2012年5月24日—2014年5月24日预见期为1～7 d的公共天气预报数据，包含了日最高气温、日最低气温以及天气类型。

1.3 ET0预报方法

1.3.1 HS法

HS公式以气温数据作为输入项计算ET0，该方法简单明了，气温预报相对准确，但是HS法未直接考虑ET0的历史变化规律，缺乏一定的物理基础。其表达式[21]为

式中ET0,HS为采用HS法计算得到的参考作物腾发量，mm/d；R为大气顶太阳辐射，MJ/(m2·d)；max、min分别为最高、最低气温，℃；为转换系数为指数系数，具有地区差异性，需要率定[24-25]。以PM公式和1999—2008年实测气象数据计算出的ET0值为基准，率定此公式中的2个参数，经2009—2011年验证期验证后，将参数应用于2012年5月24日—2014年5月24日预报期。

1.3.2 逐日均值修正法及其改进

茆智等[11]提出采用逐日均值修正法计算ET0，此法充分考虑了ET0的历史变化规律，并且结合了未来的天气预报，其表达式为

逐日均值修正法和改进逐日均值修正法中需要计算天气类型修正系数，以PM公式采用2002—2011年实测气象数据计算出逐日ET0值，并以此求出逐日多年平均ET0值，两者之比则是天气类型修正系数，据此求出12个月不同天气类型下的修正系数，应用于预报期。

1.4 参数率定以及系数计算

FAO56 PM公式为联合国粮农组织于1998年出版的ET0计算指南中提出，该法ET0计算精度高，以该公式采用历史实测气象数据的ET0计算值为准确值，其基本公式为[4]

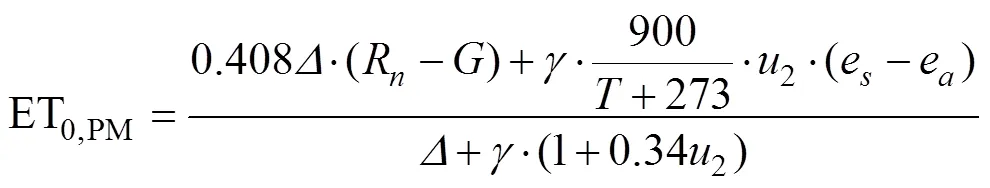
式中ET0,PM为采用PM公式计算的参考作物腾发量，mm/d；R为作物表面净辐射，MJ/(m2·d)；为土壤热通量，MJ/(m2·d)；为地面2 m高处日平均气温，℃；2为地面2 m 高处风速，m/s；e为饱和水汽压，kPa；e为实际水汽压，kPa；为饱和水汽压与气温关系曲线的斜率，kPa/℃；为湿度表常数，kPa/℃。

1.5 准确度评价指标

采用平均绝对误差（mean absolute error，MAE）、均方根误差（root mean square error，RMSE）和相关系数（correlation coefficient，）这3个统计指标来评价ET0预报的准确度，具体计算公式见文献[26]。

2 结果与分析

2.1 HS公式率定及验证

HS公式经率定后，参数校正值为0.001 9，参数校正值为0.544 6，参考胡庆芳等[25]给出的参数值分布规律，校正后的值均在给定范围（值为0.000 5～0.002，值大于0.5）之内，可以应用于ET0预报中。图2为率定后HS公式和PM公式ET0计算值（ET0,HS、ET0,PM）的散点图，从图中可以看出：率定期以及验证期的散点比较均匀地分布在线的两侧，回归直线的斜率分别为0.96、0.94。从ET0,HS的统计指标值的计算结果可以看出：率定期和验证期的MAE、RMSE均较小，相关系数均大于0.9。从总体上来说，经率定后的HS公式计算精度较高，可以应用于预报中。

图2 HS公式与PM公式的ET0计算值比较

2.2 天气类型修正系数及逐日多年平均ET0拟合

本文计算出的钟祥站点的天气类型修正系数如表2。当月份相同时，天气类型修正系数的变化规律为晴>云>阴>雨。

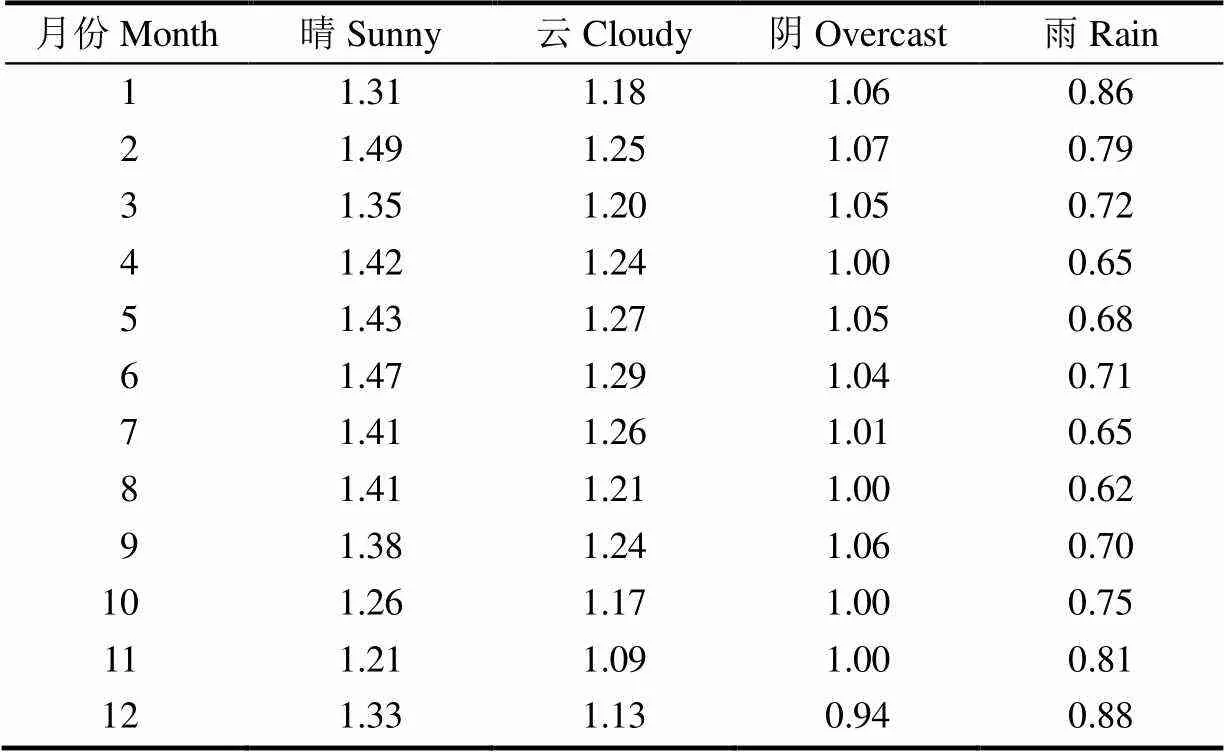
表2 钟祥天气类型修正系数

逐日均值修正法与改进逐日均值修正法的不同之处在于逐日多年平均ET0值的计算方法，前者采用茆智等[11]提出的公式计算值，后者采用ET0,PM的多年平均值，图3为2种方法计算的逐日多年平均ET0值。日序数为1～150（1—5月）时，公式计算值整体偏小，当日序数为140时，偏差最大达到1.20 mm/d；日序数为250～356（9—12月）时，公式计算值整体偏大，当日序数为251时，偏差最大达到1.29 mm/d；日序数处于150～250（6—8月）时，偏差情况比较复杂，可能是因为采用公式计算时，忽略了气候变化的复杂性，而6—8月正是气候变化最复杂的时段。从总体来说，两者偏差较大，虽然采用公式计算较简单，但是ET0,PM的多年平均值显然更为准确，可见对逐日均值法进行改进是十分必要的。

图3 逐日多年平均ET0,PM值及公式计算值比较

2.3 3种方法ET0预报精度评价

钟祥站不同预见期3种方法ET0预报值与ET0,PM计算值逐日变化过程如图4。总体而言，ET0预报值与PM公式的ET0计算值变化趋势大致相同，3种方法预报精度均较高。

图4 基于不同方法的ET0预报比较

表3为3种方法不同预见期的统计指标值，从表中可以看出：对于MAE，HS法、逐日均值修正法、改进逐日均值修正法1～7 d预见期的均值分别为0.75、0.80、0.76 mm/d；对于RMSE，3种方法的均值分别为1.00、1.07、1.05 mm/d；对于，均值分别为0.82、0.80、0.80。可见，3种预报方法精度均较高，但是总体上来说，HS法的平均绝对误差、均方根误差最小，相关系数最大，则HS法预报精度最好。相对于逐日均值修正法，改进逐日均值修正法的MAE、RMSE值均较小，预报精度更高，可见对原有公式的改进是有意义的。还可以看出，随着预见期的增长，3种预报方法的预报精度均下降。

表3 3种方法不同预见期统计指标值

结合表中的统计指标值，采用综合评价法（即总共有3个统计指标的情况下，当某一种方法有2个或3个统计指标较其他2种方法好，则该方法即为最佳ET0预报方法），得出不同预见期的最优ET0预报方法。由此得出，除了1 d预见期的最优预报方法为改进逐日均值修正法，2～7 d预见期的最优预报方法均为HS法，也表明了HS法预报精度最高。

2.4 HS法于漳河灌区适用性分析

由上述分析可知，钟祥站点ET0最优预报方法为HS法。但是对于这一结论是否可以在漳河灌区推广，需要进行进一步分析。由图1可知，除了钟祥市，漳河灌区还包括当阳市、荆州市、荆门市。对比表1中的数据，可以看出漳河灌区内部几个县市水文气象条件相似，初步认定HS法适于在整个灌区应用。

灌区内部包含2个气象站点，即钟祥站、荆州站。由上述可知2个站点水文气象条件相似，荆州站位于钟祥西南方向，荆州市以平原地区为主体、钟祥市以丘陵地区为主，地形起伏均较小。为了进一步分析HS法的适用性，于荆州站计算比较了3种预报方法的预报精度，并且绘制了该站ET0预报值与ET0,PM逐日变化过程比较图（图4c、4d）。结果表明：对于MAE，HS法、逐日均值修正法、改进逐日均值修正法1～7 d预见期的均值分别为0.72、0.90、0.71 mm/d；对于RMSE，3种方法的均值分别为0.95、1.16、0.99 mm/d；对于，均值分别为0.84、0.77、0.82。由计算结果可知，对于荆州站点，HS法仍为ET0最优预报方法。综合来看，HS法在漳河灌区内可以普遍使用。

3 讨 论

钟祥站位于华中地区，将表2与茆智等[11]给出的华北平原天气类型修正系数表进行对比。2个表格的共同点在于：当月份相同时，天气类型修正系数的变化规律为晴>云>阴>雨，这也与ET0变化规律相同；不同点在于：当月份与天气状况相同的情况下，钟祥站点的天气类型修正系数略大于华北平原，这可能与两地的气候条件有关，钟祥属于亚热带季风气候[27]，而华北平原属于暖温带季风气候[28]，钟祥站点的ET0值略大于华北平原，修正系数也略大。

HS公式预报精度总体较好，但仍存在一些误差，分析原因主要有2个方面：1）由于HS公式只考虑了气温，没有考虑诸如风速、湿度等因素[29]，当风速、湿度处于比较极限状态时，预报精度会下降[30-31]，例如2013年8月7日，1 d预见期的预报最低、最高温只与实际值相差分别为0.4、0.3 ℃，而平均风速达到3.1 m/s，导致当日ET0,PM为7.475 mm/d，预报值仅为4.579 mm/d；2）由于气温预报的误差，导致ET0,PM与预报值相差较大，例如2013年6月11日，当日实际最高气温为27.6 ℃，而1 d预见期的预报最高气温仅为22 ℃，因此ET0,PM为5.231 mm/d，而预报值仅为2.530 mm/d。

由于逐日均值修正法中只划分了4个基本的天气类型，而实际情况中远不止4种，因此产生了ET0预报误差，同时该方法中采用的多年平均ET0为公式计算的结果，也是产生误差的原因。例如2013年3月9日，对于当天ET0的多年平均值，逐日均值修正法采用1.505 mm/d，改进逐日均值修正法中采用2.543 mm/d，从而导致该天ET0,PM为3.508 mm/d，改进逐日均值修正法时1 d预见期的预报值为3.063 mm/d，而逐日均值修正法时的预报值仅为1.813 mm/d。

天气类型修正系数是通过ET0,PM计算的，由于ET0,PM计算过程中包含了风速、湿度等气象数据，因此改进逐日均值修正法中也间接地考虑了风速、湿度等气象因素的影响，可是天气类型划分过少，产生了预报误差。例如2012年7月25日，1 d预见期预报的天气类型为阵雨，但是直接采用了天气类型为“雨”的修正系数，选用的修正系数偏小，导致预报值为2.539 mm/d，而ET0,PM为6.091 mm/d。

茆智等[11]提出的逐日均值修正法具有广泛的应用性，但是该方法用指数函数拟合多年平均值，其预报精度仍有待提高，因此尝试利用历史资料计算出的结果代替公式拟合值，提出了改进逐日均值修正法。经分析计算，改进后的逐日均值修正法提高了ET0预报精度。此次选取的3种ET0预报方法皆是基于天气预报数据，并且通过对3种方法的适用性分析，得到适合漳河灌区的精度较高的ET0预报方法。

文中虽然得出了钟祥站最优预报方法为HS法，且验证了该方法在漳河灌区的适用性。但是，由于HS方法只利用了气温资料，不可避免地造成了误差，在以后的研究中可以对HS公式进行适当改进，加入其他气象因素，以期提高预报精度。此次只研究了ET0预报方法，今后可以考虑加入作物系数的研究，以便得到精确的作物需水量预报，为灌溉预报提供数据基础。

4 结 论

本文以钟祥站为例，分别比较了HS法、逐日均值修正法和改进逐日均值修正法的预报精度。并且通过水文气象条件以及与荆州站点结果进行对比，分析了预报方法在漳河灌区的适用性。主要结论如下：

1）HS法中参数具有明显的地区性，经参数校正后，率定期以及验证期趋势线斜率接近于1，MAE、RMSE均较小，相关系数均大于0.9，ET0计算精度大幅度提升，对于ET0预报十分有利。

2）天气类型修正系数虽然随着地区、月份以及天气状况不同而变化，但是其变化规律与ET0变化规律相同。对于逐日多年平均ET0值的计算，公式计算结果与ET0,PM的多年平均值相差较大，表明对逐日均值修正法进行改进，可以大幅度提升预报精度。

3）对于钟祥站点而言，HS法预报精度最好，改进逐日均值修正法次之，逐日均值修正法最差。HS法预报误差主要源于没有考虑风速、湿度等气象因素以及气温预报误差，逐日均值修正法和改进逐日均值修正法误差主要源于天气类型划分过少，与实际不符。经过水文气象条件分析以及与荆州站点计算结果对比，表明HS法可以在漳河灌区内普遍使用。

[1] 王立坤，刘庆华，付强. 时间序列分析法在水稻需水量预测中的应用[J]. 东北农业大学学报，2004，35(2)：176－180. Wang Likun, Liu Qinghua, Fu Qiang. Applying the method of time series analysis to forecasting the paddy water requirement[J]. Journal of Northeast Agricultural University, 2004, 35(2): 176－180. (in Chinese with English abstract)

[2] 赵博. 通过农业用水权转让缓解我国水资源短缺[J]. 水利科技与经济，2011，17(9)：1－5. Zhao Bo. Relieving the China’s water shortage through the irrigation water trade[J]. Water Conservancy Science & Technology & Economy, 2011, 17(9): 1－5. (in Chinese with English abstract)

[3] 徐凯，陆垂裕，季海萍. 作物蒸发腾发量计算研究综述[J]. 人民黄河，2013，35(4)：61－65. Xu Kai, Lu Chuiyu, Ji Haiping. Review on calculation methods for crop evapotranspiration[J]. Yellow River, 2013, 35(4): 61－65. (in Chinese with English abstract)

[4] Allen R G, Pereira L S, Raes D, et al. Crop evapotranspiration-Guidelines for computing crop water requirements[R]//FAO Irrigation and Drainage Paper 56. Rome: FAO, 1998.

[5] 蔡甲冰，刘钰，雷廷武，等. 根据天气预报估算参照腾发量[J]. 农业工程学报，2005，21(11)：11－15. Cai Jiabing , Liu Yu, Lei Tingwu, et al. Daily reference evapotranspiration estimation from weather forecast messages[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(11): 11－15. (in Chinese with English abstract)

[6] 张倩，蔡焕杰，魏新光，等. 基于主成分分析的参考作物腾发量预测研究[J]. 节水灌溉，2010(12)：64－66. Zhang Qian, Cai Huanjie, Wei Xinguang, et al. Research on reference crop evapotranspiration prediction based on PCA[J]. Water Saving Irrigation, 2010(12): 64－66. (in Chinese with English abstract)

[7] Zhang Tibin, Kang Yaohu, Wan Shuqin. Shallow sand-filled niches beneath drip emitters made reclamation of an impermeable saline-sodic soil possible while cropping with[J]. Agricultural Water Management, 2013, 119: 54－64.

[8] 常晓敏，高占义，王少丽，等. 基于气温预报和HS公式的不同生育期参考作物腾发量预报[J]. 节水灌溉，2016(8)：169－174. Chang Xiaomin, Gao Zhanyi, Wang Shaoli, et al. Different growth period forecasting reference crop evapotranspiration based on temperature forecast and Hargreaves-Samani equation[J]. Water Saving Irrigation, 2016(8): 169－174. (in Chinese with English abstract)

[9] Perera K C, Western A W, Nawarathna B, et al. Forecasting daily reference evapotranspiration for Australia using numerical weather prediction outputs[J]. Agricultural and Forest Meteorology, 2014, 194(3): 50－63.

[10] Mao Zhi. Forecast of crop evapotranspiration[J]. ICID Bulletin, 1994, 43(1): 23－36.

[11] 茆智，李远华，李会昌. 逐日作物需水量预测数学模型研究[J]. 武汉大学学报：工学版，1995，28(3)：253－259. Mao Zhi, Li Yuanhua, Li Huichang. Study of mathematic model for forecasting daily crop evapotranspiration[J]. Journal of Wuhan University of Hydraulic & Electric Engineering, 1995, 28(3): 253－259. (in Chinese with English abstract)

[12] Mohan S, Arumugam N. Forecasting weekly reference crop evapotranspiration series[J]. Hydrological Sciences Journal, 1995, 40(6): 689－702.

[13] 蔡学良，崔远来，宋志强，等. 陡山灌区实时灌溉预报研究[J]. 灌溉排水学报，2003，22(3)：33－36. Cai Xueliang, Cui Yuanlai, Song Zhiqiang, et al. Study on real-time irrigation forecasting in Doushan Irrigation Scheme[J]. Journal of Irrigation & Drainage, 2003, 22(3): 33－36. (in Chinese with English abstract)

[14] 蔡甲冰，刘钰，雷廷武，等. 根据天气预报估算参照腾发量[J]. 农业工程学报，2005，21(11)：11－15. Cai Jiabing, Liu Yu, Lei Tingwu, et al. Daily reference evapotranspiration estimation from weather forecast messages-the ANFIS method[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2005, 21(11): 11－15. (in Chinese with English abstract)

[15] Cai Jiabing, Liu Yu, Lei Tingwu, et al. Estimating reference evapotranspiration with the FAO Penman-Monteith equation using daily weather forecast messages[J]. Agricultural and Forest Meteorology, 2007, 145(1–2):22-35.

[16] 赵琪，罗玉峰，彭世彰，等. 基于天气预报和Penman- Monteith公式的短期逐日参考作物腾发量预报[J]. 节水灌溉，2014(1)：1－4. Zhao Qi, Luo Yufeng, Peng Shizhang, et al. Short-term daily reference crop evapotranspiration forecast based on weather forecast and Penman-Monteith equation[J]. Water Saving Irrigation, 2014(1)：1－4. (in Chinese with English abstract)

[17] 罗玉峰，李思，彭世彰，等. 基于气温预报和HS公式的参考作物腾发量预报[J]. 排灌机械工程学报，2013，31(11)：987－992. Luo Yufeng, Li Si, Peng Shizhang, et al. Forecasting reference crop evapotranspiration based on temperature forecast and Hargreaves-Samani equation[J]. Journal of Drainage & Irrigation Machinery Engineering, 2013, 31(11): 987－992. (in Chinese with English abstract)

[18] Luo Yufeng, Chang Xiaomin, Peng Shizhang, et al. Short-term forecasting of daily reference evapotranspiration using the Hargreaves– Samani model and temperature forecasts[J]. Agricultural Water Management, 2014, 136(2): 42－51.

[19] 罗玉峰，崔远来，蔡学良. 参考作物腾发量预报的傅立叶级数模型[J]. 武汉大学学报：工学版，2005，38(6)：45－47. Luo Yufeng, Cui Yuanlai, Cai Xueliang. A Fourier series model for forecasting reference crop evapotranspiration[J]. Journal of Wuhan University of Hydraulic & Electric Engineering, 2005, 38(6): 45－47. (in Chinese with English abstract)

[20] 李晨，崔宁博，魏新平，等. 改进Hargreaves模型估算川中丘陵区参考作物蒸散量[J]. 农业工程学报, 2015，31(11)：129－135. Li Chen, Cui Ningbo, Wei Xinping, et al. Improvement of Hargreaves method for reference evapotranspiration in hilly area of central Sichuan Basin[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(11): 129－135. (in Chinese with English abstract)

[21] 唐晓培，宋妮，陶国通，等. 黄淮海地区Hargreaves 公式主要参数的空间化处理[J]. 农业工程学报，2016，32(增刊1)：63－70. Tang Xiaopei, Song Ni, Tao Guotong, et al. Spatial distribution of main parameters of Hargreaves formula in typical time scales in Huang-Huai-Hai Plain[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(Supp 1): 63－70. (in Chinese with English abstract)

[22] 李远华，崔远来，杨常武，等. 漳河灌区实时灌溉预报研究[J]. 水科学进展，1997，8(sk)：71－77. Li Yuanhua, Cui Yuanlai, Yang Changwu, et al. A study on real time irrigation forecasting in the Zhanghe Irrigation Schome[J]. Advances in Water Science, 1997, 8(sk): 71－77. (in Chinese with English abstract)

[23] 顾世祥，何大明，李远华，等. 逐日参照腾发量预测的改进方法[J]. 水利学报，2005，36(11)：1292－1297. Gu Shixiang, He Daming, Li Yuanhua, et al. Improved method for daily evapotranspiration prediction[J]. Journal of Hydraulic Engineering, 2005, 36(11): 1292－1297. (in Chinese with English abstract)

[24] Hargreaves G H, Allen R G. History and evaluation of Hargreaves evapotranspiration equation[J]. Journal of Irrigation & Drainage Engineering, 2003, 129(1): 53－63.

[25] 胡庆芳，杨大文，王银堂, 等. Hargreaves公式的全局校正及适用性评价[J]. 水科学进展，2011，22(2)：160－167. Hu Qingfang, Yang Dawen, Wang Yintang, et al. Global calibration of Hargreaves equation and its applicability in China[J]. Advances in Water Science, 2011, 22(2): 160－167. (in Chinese with English abstract)

[26] Yang Yang, Cui Yuanlai, Luo Yufeng, et al. Short-term forecasting of daily reference evapotranspiration using the Penman-Monteith model and public weather forecasts[J]. Agricultural Water Management, 2016, 177: 329－339.

[27] 林长洲. 钟祥市志[M]. 武汉：湖北长江出版社，2013.

[28] 孙鸿烈. 中国资源科学百科全书[M]. 北京：中国石油大学出版社，2000.

[29] Vanderlinden K, Giraldez J V, Van Meirvenne M. Assessing reference evapotranspiration by the Hargreaves method in southern Spain[J]. journal of Irrigation and Drainage Engineering, 2004, 130(3): 184－191.

[30] Droogers P, Allen R G. Estimating reference evapotranspiration under inaccurate data conditions[J]. Irrigation & Drainage Systems, 2002, 16(1): 33－45.

[31] Bakhtiari B, Ghahraman N, Liaghat A M, et al. Evaluation of reference evapotranspiration models for a semiarid environment using lysimeter measurements[J]. Journal of Agricultural Science & Technology, 2011, 13(2): 223－237.

刘 梦，罗玉峰，汪文超，何 军，崔远来. 基于天气预报的漳河灌区参考作物腾发量预报方法比较[J]. 农业工程学报，2017，33(19)：156－162. doi：10.11975/j.issn.1002-6819.2017.19.020 http://www.tcsae.org

Liu Meng, Luo Yufeng, Wang Wenchao, He Jun, Cui Yuanlai. Comparison of three reference crop evapotranspiration forecasting methods based on short-term weather forecast in Zhanghe irrigation district[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(19): 156－162. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.19.020 http://www.tcsae.org

Comparison of three reference crop evapotranspiration forecasting methods based on short-term weather forecast in Zhanghe irrigation district

Liu Meng1, Luo Yufeng1※, Wang Wenchao1, He Jun1,2, Cui Yuanlai1

(1.430072,; 2.443002,)

Reference crop evapotranspiration (ET0) forecasting is important for real time irrigation scheduling. In this paper we improved the daily average modification method (DAM) and compared 3 ET0forecasting methods including the Hargreaves-Samani (HS) model, DAM and improved daily average modification method (iDAM) for their accuracy in Zhanghe irrigation district. The data of annual sunshine duration, annual average temperature and annual precipitation of each meteorological stations in Zhanghe irrigation district were collected. The deviation range of these 3 factors were from –2.7% to 7.7%, from –1.2% to 1.2%, from –3.7% to 23.4%. The HS model was also improved for the local use. The ET0calculated by FAO56-Penman-Monteith (PM) model was used as the control. In the DAM model, the daily annual average value of ET0was estimated by fitness, which could introduce fitness error in the ET0estimation. Thus, we improved the DAM by using the real observed historical meteorological data to calculate the daily annual average value of ET0. Daily historical meteorological data of Zhongxiang and Jingzhou Station for the period from January 1, 1999 to May 24, 2014 and the public weather forecasts of 7 days ahead from May 24, 2012 to May 24, 2014 were collected. The historical data were used to calculate the value of ET0by PM model and the ET0calculated for the period 1999-2008 and 2002-2011 were used to calibrate HS model and get the correction factors of weather type. The weather were classified into 4 types. The 3 methods were used to forecast ET0from May 24, 2012 to May 24, 2014. The results showed that the mean absolute error (MAE) of the HS model in the calibration period and validation period were 0.46 and 0.46 mm/d, respectively. The root mean square error (RMSE) was 0.63 and 0.64 mm/d and the correlation coefficients were 0.92 and 0.91, respectively. It indicated that the improved HS model was suitable for ET0estimation in Zhanghe irrigation district. The correction factors of weather type in Zhongxiang station were highest in the sunny day, followed by the cloudy, overcast and rainy day. The values were higher than North China Plain. The daily annual average value of ET0by DAM was smaller in the days of 1-150 but higher in the 250-356 days, indicating that the improvement of DAM was necessary. In the Zhongxiang station, the MAE of HS model, DAM and iDAM methods were 0.75, 0.80, 0.76 mm/d, RMSE were 1.00, 1.07, 1.05 mm/d, and correlation coefficients were 0.82, 0.80, 0.80, respectively. In Jingzhou station, the MAE of the 3 methods above were 0.72, 0.90, 0.71 mm/d, RMSE were 0.95, 1.16, 0.99 mm/d, correlation coefficients were 0.84, 0.77, 0.82. Among the 3 methods, the iDAM method had the highest accuracy for the forecast horizon of 1 day but the HS method was the best for the forecast horizon of 2-7 days. With the increase of forecast period, the MAE and RMSE increased, indicating that the forecast accuracy decreased. Overall, the 3 proposed methods were well for ET0forecasting and the best method was the HS model. In future, we can try to forecast ET0usingthe HS model for irrigation forecast in Zhanghe irrigation district.

evapotranspiration; weather forecast; temperature; Hargreaves-Samani; daily average modification method

10.11975/j.issn.1002-6819.2017.19.020

S161.4

A

1002-6819(2017)-19-0156-07

2017-03-29

2017-08-10

国家重点研发计划项目（2017YFC0403200）；水资源与水电工程科学国家重点实验室开放研究基金资助项目（2013B110）

刘 梦，湖北仙桃人，主要从事水稻节水灌溉理论与技术。 Email：373832607@qq.com

※通信作者：罗玉峰，江西遂川人，教授，博士，博导，主要从事水稻节水灌溉理论与技术及智慧灌溉研究。Email：yfluo@whu.edu.cn

中国农业工程学会会员：罗玉峰（E041100001M）