基于FPGA的电力电子变换器的精仿真研究
于 飞,刘彦志
(青岛科技大学 自动化与电子工程学院,山东 青岛 266042)
基于FPGA的电力电子变换器的精仿真研究
于 飞,刘彦志
(青岛科技大学 自动化与电子工程学院,山东 青岛 266042)
在电力电子仿真领域,基于现场可编程门阵列(FPGA)高速并行运算的特点,为了达到实时效果,对系统模型通常采用较为方便的建模;提出了使用FPGA对Boost变换器进行复杂建模以及算法研究;基于这一思想,首先对boost变换器进行建模以及算法研究;其次完成基于FPGA的Boost变换器的建模并利用XILINX的ML605开发板进行仿真实验,将仿真波形与MATLAB进行对比,证实了在一定误差范围内,基于FPGA复杂建模仿真的有效性及准确性。
Boost变换器;FPGA;数学模型;龙格库塔
0 引言
在电力系统仿真领域,随着新一代的电网以及输配电系统发展,大量电力电子器件的引入以及更高的频率,对模型仿真计算性能的要求越来越高,并行计算是目前解决单处理器速度瓶颈的最好方法之一[1]。当前主流的实时仿真系统中,如RTDS、Hypersim、dSPACE都采用多块CPU或DSP并行方式运行,但其并行度有限;而FPGA具有高度并行性特性以及可重构计算方式,特别适合用来对具有高度并行特点的电力电子模型进行仿真。对于复杂的系统模型,虽然采样率高,但只要是并行运算,模型的复杂程度并不会影响速度[2]。
随着电力电子模块化结构以及分布式电源接入配电网的不断发展,FPGA凭借其高速并行处理能力、流水型架构和内存分布性,使其越来越多的应用于电力电子分布式控制、模块化电力电子设备的建模仿真中[3-6]。文献[7]提出了利用FPGA完成PLC体系复杂算法并行处理的方法,将PLC的运算速度提高到了50 ns级别。
解析法是基于变换器特性的建模方法,而状态空间平均法则是解析法中最具有代表性的方法之一。为了提高仿真的精度以及快速分析的能力]。文献[8]使用全局隐式梯形积分法,利用后向欧拉法对开关动作点进行线性插值计算,以此来提高精度和计算速度。文献[9]采用了一种2阶隐式龙格库塔法建立等值模型,并在此数值积分方法上运用了开关自校正插值的方法。龙格库塔是求解常微分方程的数值方法,虽然4阶龙格库塔法具有较高的精度,但是对步长有限制,使用4阶龙格库塔法必须保证步长在绝对稳定域之内,因此对高频开关器件电路,只要保证步长满足要求,使用4阶龙格库塔法也可以获得较高精度的仿真波形。
1 Boost变换器的数学建模
Boost变换器电路原理如图1所示,Boost变换器的工作模式分为两种:电感电流连续工作模式和电感电流断续工作模式。
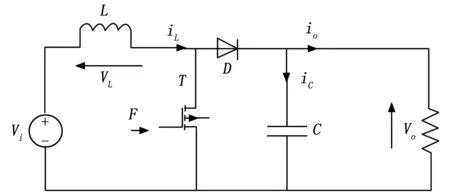
图1 Boost变换器的电路原理图
图2所示的电路工作状态为理想状态下的电路变化,即开关管和二极管导通状态电阻为零,开关管和二极管关断状态电阻无限大。其中图2(a)和图2(b)所示为电流连续工作模式的电路工作状态,图2(a)、(b)、(c)所示为电流断续工作模式的电路工作状态,电流断续工作模式是由于采用小电感,导致多出一个电感为零的工作状态。本文主要对电流连续工作模式进行相关建模以及仿真研究。
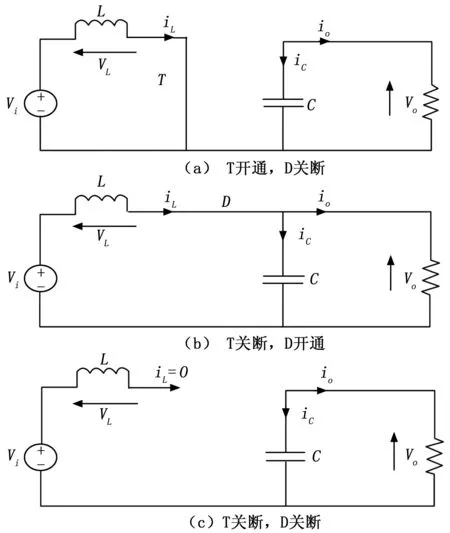
图2 T开通,D关断
为了简单直观地反映对Boost变换器建模不同所导致的仿真波形的差异,采用最常用的开环控制策略对开关管进行控制,开关频率通过控制电压vm与三角波vc进行比较得来,开关管的控制F由vm-vt决定。
由图2所示Boost变换器电路工作状态的变化,可以对Boost变换器建立理想数学模型,列出电感电压vL(t)和电容电流ic(t)的表达式:
vL(t)=vi(t)*F+(vi(t)-v0(t)*F*sign(iL)
ic(t)=-i0(t)*F+iL(t)*F*singn(iL)
(2)
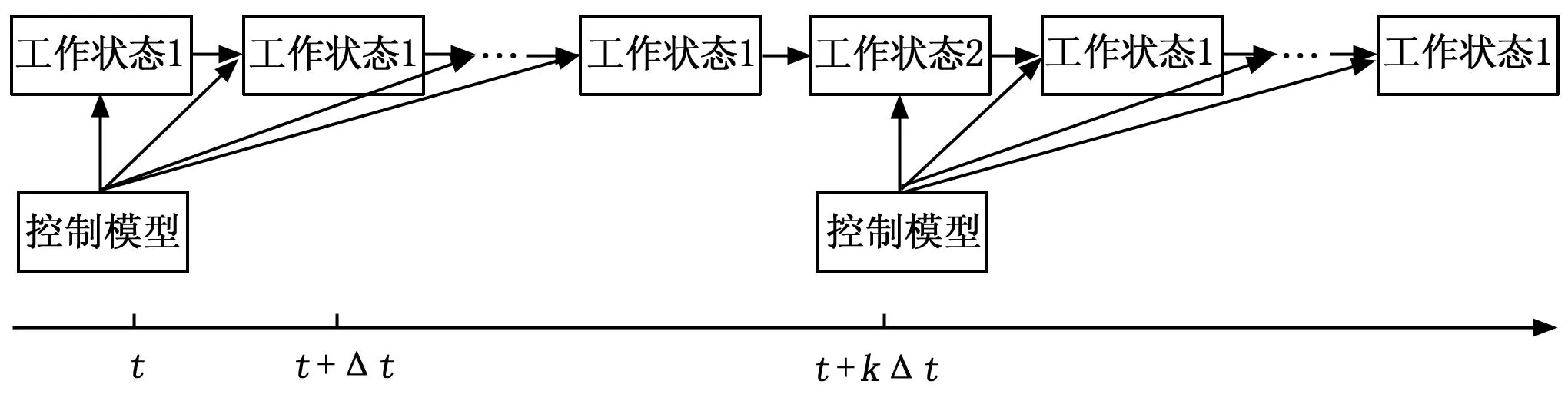
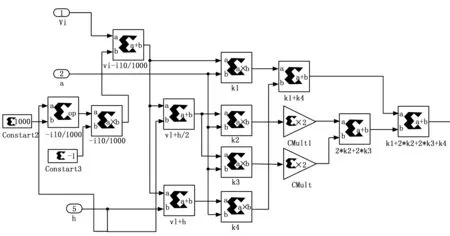
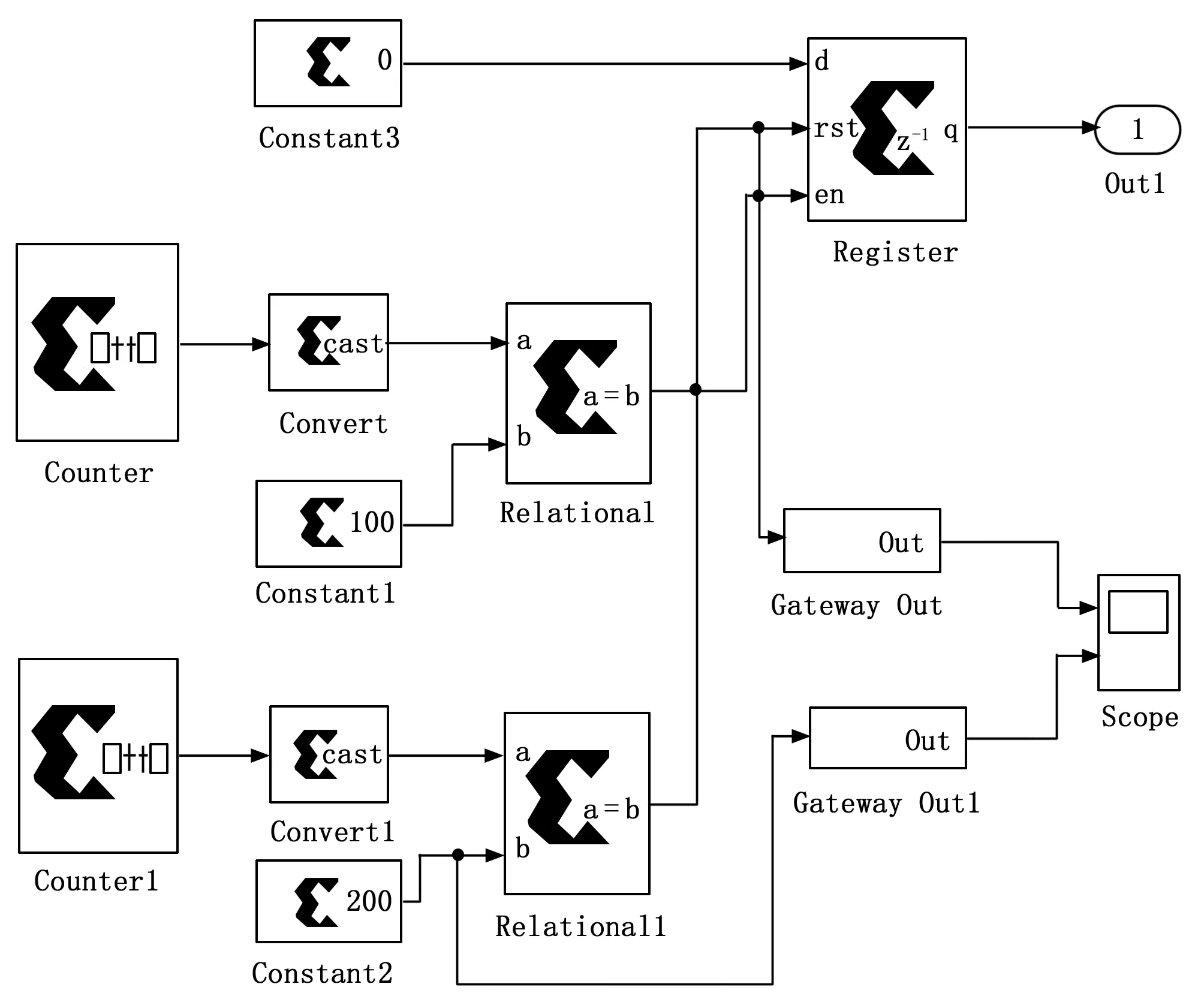
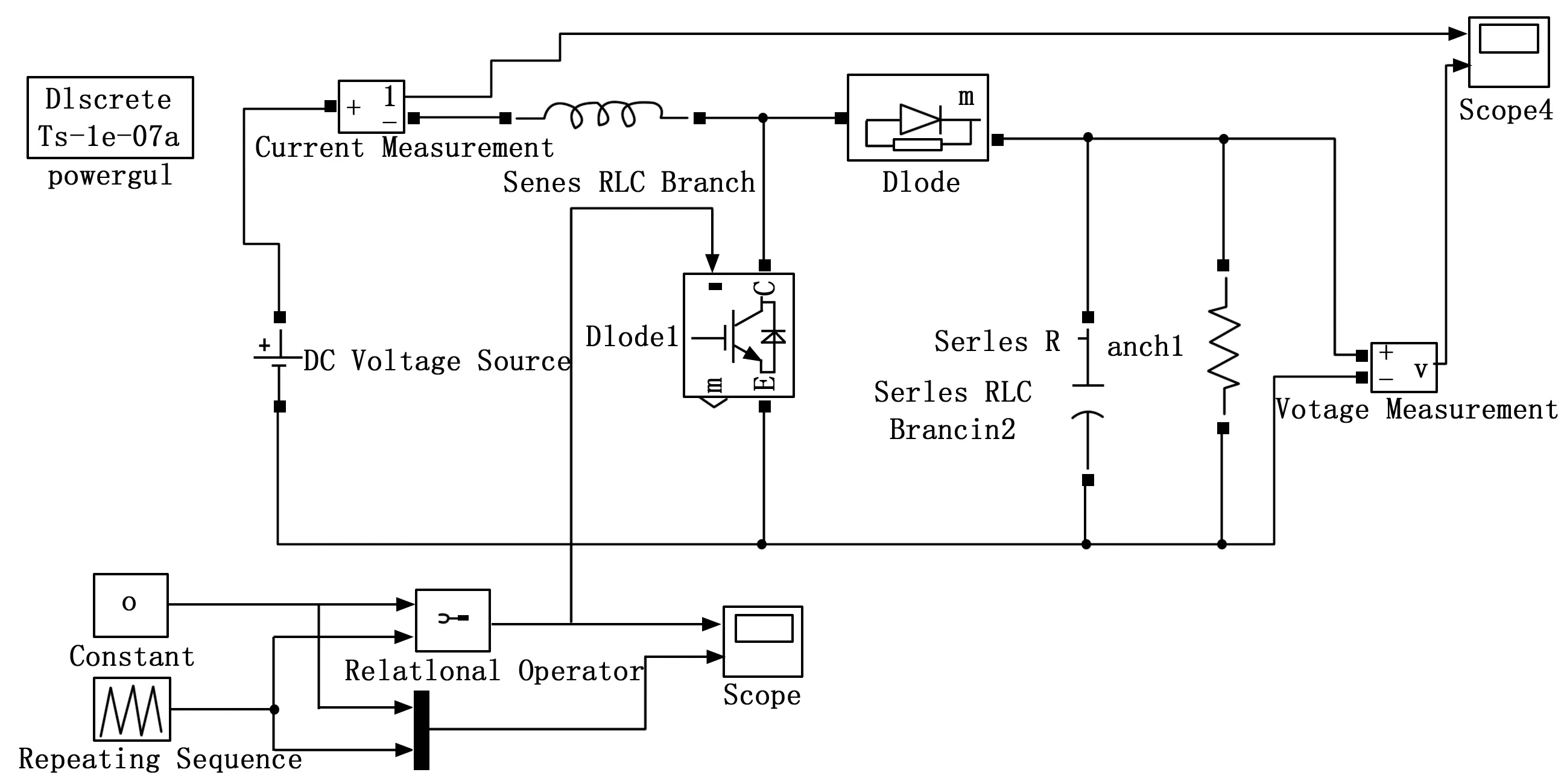
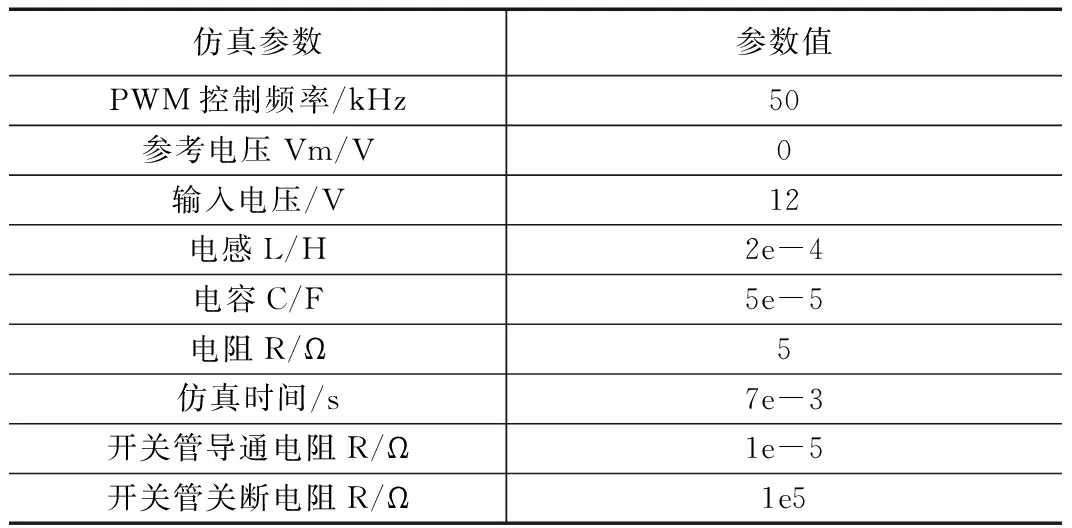
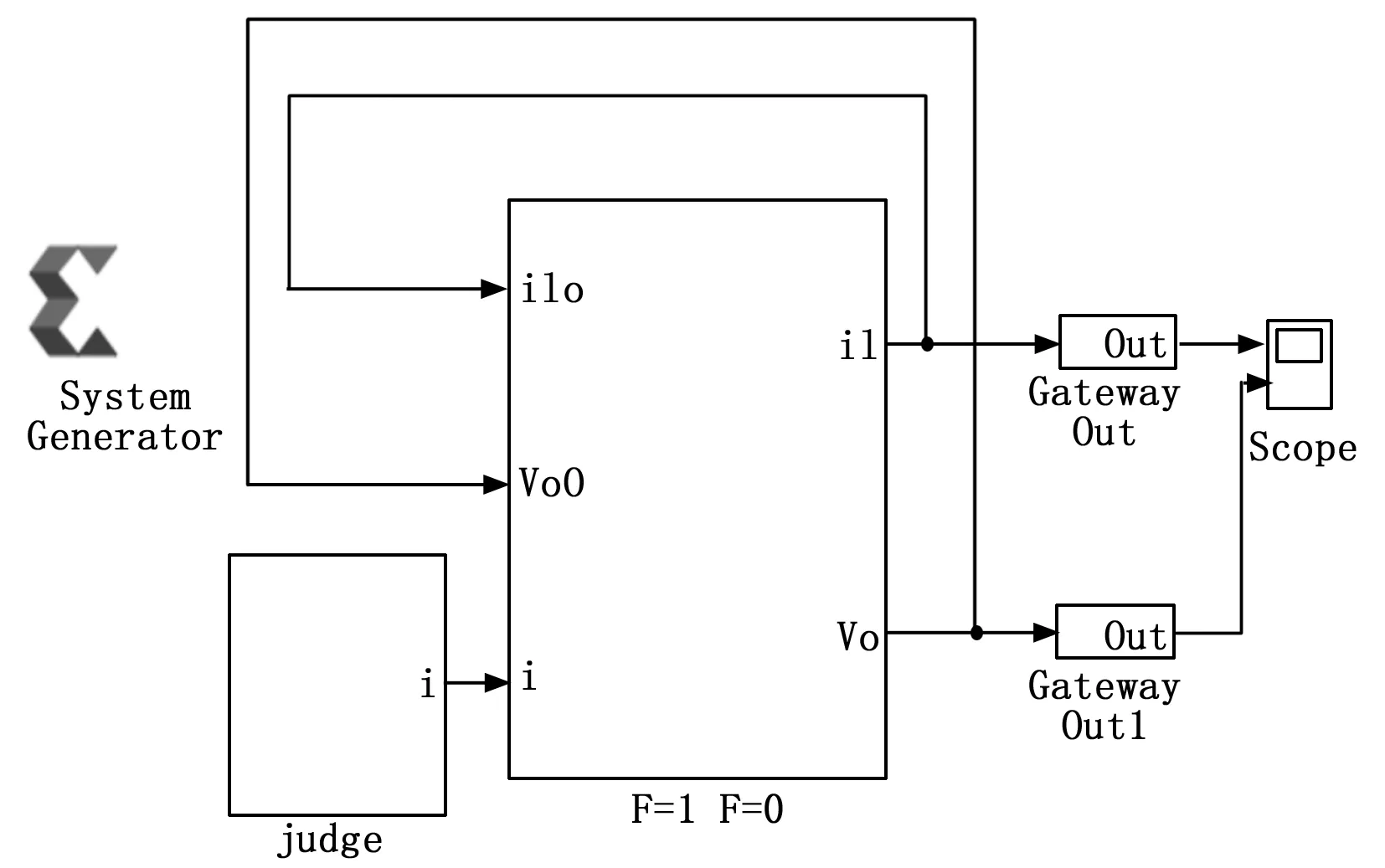
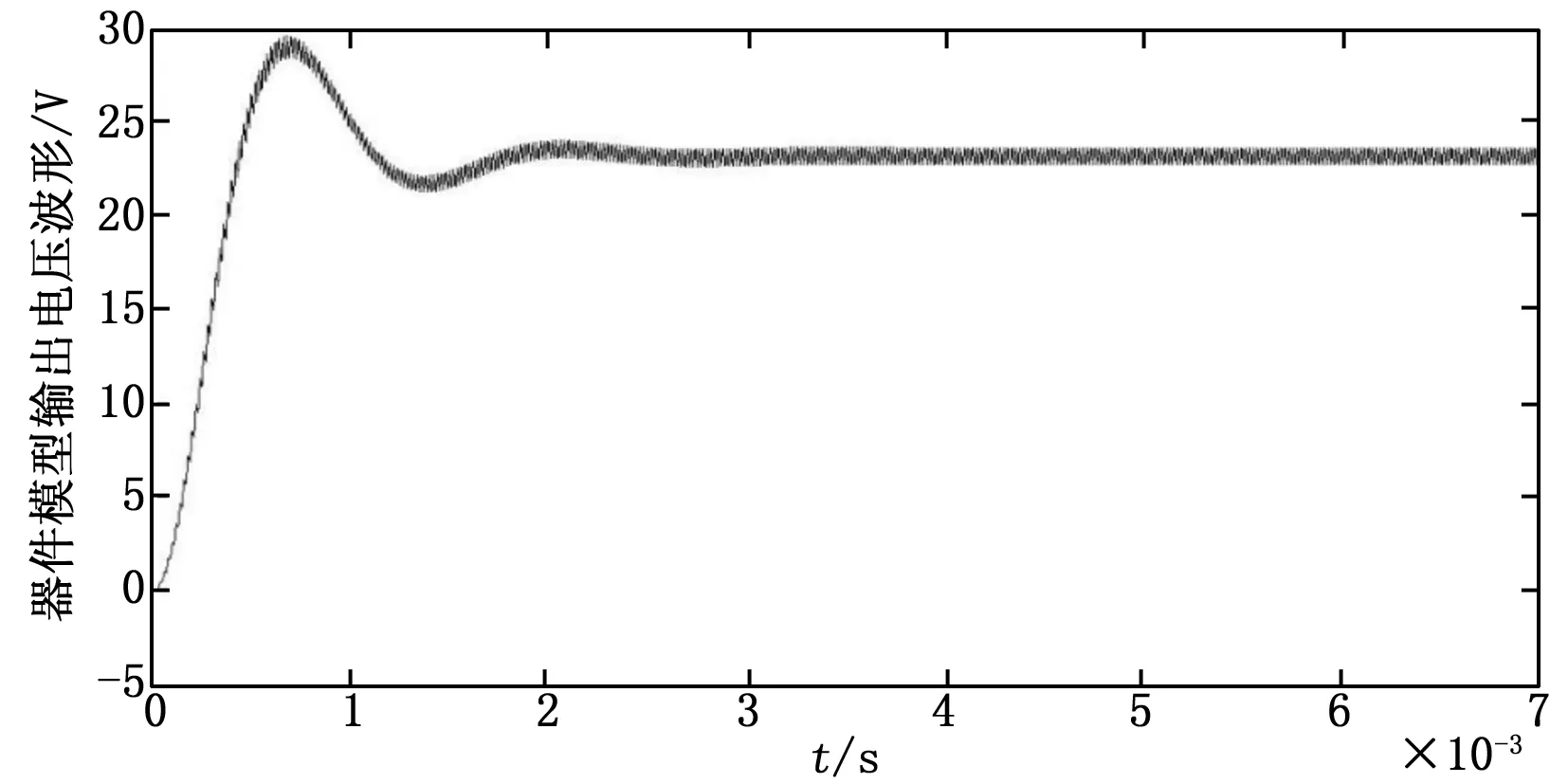
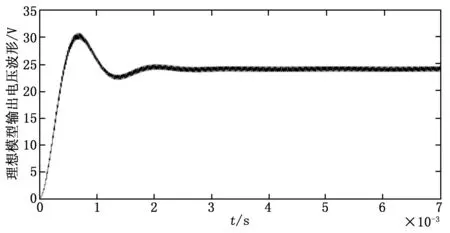
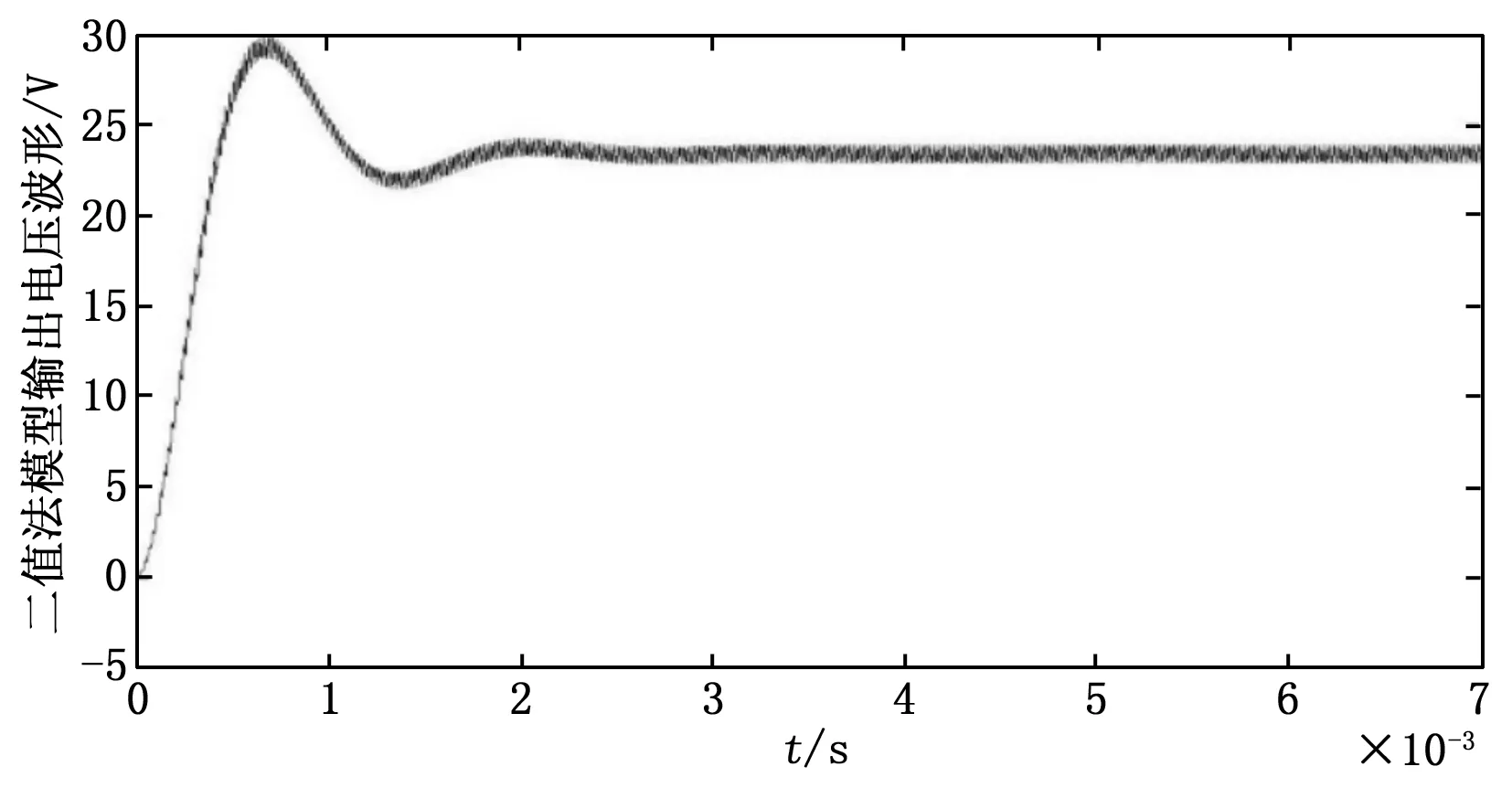
式中,F是一个逻辑变量,当时vm≥vt,F=1,当时vm 对Boost变换器进行状态空间表达式建模,状态空间表达式描述如下: (3) (4) 要保证4阶龙格库塔法能稳定,需要对其绝对稳定域进行分析计算,假设参考模型为: (5) 工作状态1时,对式(1)和(2)使用4阶龙格库塔离散化状态空间方程,如下: (6) (7) 同理,工作状态2时,离散化4阶龙格库塔理想状态空间方程如下: (8) (9) 为了建立更准确的数学模型,本文将开关器件用二值法等效,即将开关开通状态和关断状态分别等效成小电阻和大电阻,然后利用节点法分析电路,获得高维度的导纳矩阵方程。在对电感和电容的离散化过程中,为了使结果更具有对比性,同样使用4阶龙格库塔法进行数值计算。 FPGA与传统的CPU仿真相比,具有并行计算优势和更高的设计灵活性,满足高速精仿真需求。传统的FPGA代码编写流程十分繁杂,工作量大,而且需要对具体的FPGA芯片有较深入的了解,System Generator的出现极大的降低了FPGA设计开发难度,即使对硬件不算了解,也能进行程序设计。本文利用System Generator进行Boost变换器的模型搭建,System Generator是MATLAB/Simulink环境下一款理想的FPGA开发软件,也可以认为是Simulink中的工具包,可以自动的将设计模型转化为硬件实现,而无需掌握复杂的VHDL或Verilog语言。FPGA作为一种并行计算设备,可以快速有效地进行数据计算处理,为高速电力电子仿真提供了合适的环境。FPGA通过将串行计算中的并行计算变为并行计算,将极大地减少运算的时间。假设式(6)、(7)中每一个式子都只有一步运算,如果采用串行计算,将进行5步运算,而并行运算只需要2步,即在运算中K1、K2、K3、K4可以同步计算。 变换器模型的并行计算方法步骤如下图3所示。由于变换器模型较为简单,解算规模较为适中,本文以控制器模型的开关周期为一个控制模型步长,以变换器模型Δt=h为变换器模型步长,仅考虑控制模型为变换器模型解算步长整数倍的情况。 图3 变换器模型求解计算时序 图5 4阶龙格库塔模型 图3可知给出了控制模型解算步长为变换器模型解算步长倍的时序,即控制模型计算一次时,变换器模型计算次。变换器模型由时刻积分到时刻的一个步长中,采用时刻的值作为工作状态1的输入,当变换器模型完成一个解算步长之后,需要将上一个状态的输出变量用作此次积分计算的输入值。每个工作状态里开关的等效值会根据状态的不同进行改变,在到时刻的积分计算过程中,一个工作状态的求解结果会更新到另一个工作状态中,依次进行计算求解。在一个开关周期内即在第一个控制模型步长内,根据工作状态1中的式(6)、(7)解算出电路的各个变量状态值以及等效值等输出值,作为输入值更新到工作状态2中;在第二个控制模型步长中,根据式(8)、(9)对变换器模型重新进行积分计算,完成一个工作周期。 首先根据变换器原理图建立器件模型,然后利用MATLAB对建立的数学模型进行编程仿真,最后在MATLAB的基础上,使用System Generator对变换器模型进行搭建,模型的搭建过程按照模块化搭建方式分步进行,对可重复利用的子模块进行搭建,将可以减少搭建的复杂程度、节约时间,同时理解方便增加了设计的可读性。 2.2.1 PWM控制模型 由于对Boost变换器采用的是简单的开环控制,PWM控制信号为固定占空比的方波,由参考电压与一个固定频率与峰值的三角波相比较实现,其中参考电压,占空比为。图4为PWM控制模型,使用两个counter计数器相差2倍的关系来产生三角波,再通过三角波与参考电压对比得到控制信号,当参考电压大于三角波时输出高电平,反之输出低电平。系统时钟为10 MHz,PWM频率为50 kHz,计数器的计数值分别设为100和200。 图4 PWM模型 2.2.2 4阶龙格库塔的模型 按照建立的Boost变换器的数学模型,用XILINXBlockset库中的模块进行模型的搭建设计。如图5所示,为搭建的4阶龙格库塔模型。在进行整体模型设计的过程中,可以将4阶龙格库塔模型作为一个子模块,重复使用子模块以减少工作的重复性。从图5所示的模型的搭建过程中可以看出,该模型是按照并行的方式进行搭建的。 2.2.3 缓冲寄存器模块 图6 Boost变换器器件模型及控制器模型 式(8)的并行运算步骤: 2)计算iC(t)的值; 4)计算K2、K3、K4的值; 5)计算2*K2、2*K3的值; 6)计算K1+2*K2+2*K3+K4的值; 8)计算v0(t+1)的值。 式(9)的并行运算步骤: 3)计算K2、K3、K4的值; 4)计算2*K2、2*K3的值; 5)计算K1+2*K2+2*K3+K4的值; 7)计算v0(t+1)的值。 将建好的变换器模型和控制器模型通过JTAG下载到FPGA中,本文利用XILINX的Virtex-6FPGAML605进行实物仿真。 在对Boost变换器数学模型研究的基础上,本文对Boost变换器理想状态空间模型、二值状态空间模型和PWM控制器模型进行建模仿真,其中控制器以及Boost变换器建模仿真中各个参数设置如表1所示。 表1 仿真参数列表 本文为了验证FPGA对复杂模型仿真的精度与仿真的可行性,并适当地提高仿真速度,因此分别对Boost变换器和控制器进行建模,对控制模型设置仿真步长为10 μs,对器件模型仿真和复杂模型仿真设置仿真步长为200 ns,仿真时间均为7 ms,Simulink系统周期与FPGA系统时间周期一致为10 ns。图6为Boost变换器器件模型,图7为Boost变换器复杂模型与控制器模型。 进行仿真分析时,需要将图7所建立的模型通过JTAG下载到FPGA中,得到输出电压波形,将仿真波形与按照图6进行的MATLAB仿真产生的波形进行对比。图8~10分别为Matlab/Simulink器件模型的仿真、基于FPGA的理想以及复杂模型。 图7 Boost变换器模型及控制器模型 图8 Boost变换器器件模型输出电压波形 图8与图9对比可以看出,理想状态空间模型与器件模型相比,虽然波形响应基本一致,但是电压的幅值存在着一定的误差;图8和图10对比可以看出,随着建模精确度的提高,基于二值法的模型与器件模型相比,波形基本一致,验证了基 图9 Boost变换器理想模型输出电压波形 图10 Boost变换器二值法模型输出电压波形 于FPGA复杂建模仿真的有效性与准确性。 FPGA并行数据处理能力强、可重构的特点,基于FPGA的电力电子仿真技术研究一直是国内外学者研究的重点。本文在研究了国内外仿真算法的基础上,构建了电力电子控制模型以及利用4阶龙格库塔法对Boost变换器构建了理想数学模型和复杂的数学模型,对比输出电压得出,基于FPGA的电力系统的高精度建模仿真的准确性与有效性。 [1] 陆臻业,邹毅军,王 佳,等.一种基于FPGA的高速电力电子实时仿真方法研究[J]. 电气自动化,2016,38(5):18-21. [2]付志红,马 静,谢品芳,等. 基于高速数字信号处理平台的实时仿真技术[J].系统仿真学报,2007,19(6):3680-3683. [3] 牟昱东,张建文,朱 淼,等. 基于FPGA的模块化通用型电力电子控制平台[J]. 电力电子技术,2016,50(8):106-108. [4] 刘喜梅,李梅航,朱 炯,等. 模块化多电平换流器子模块等效数学模型的建立及仿真[J]. 青岛科技大学学报(自然科学版),2016,37(1):91-96. [5] Guillaud X,Faruque M O,Teninge A,et al. Applications of Real-Time Simulation Technologies in Power and Energy Systems[J]. IEEE Power and Energy Technology Systems,2015,2(3):103-115. [6] 王成山,丁承第,李 鹏,等. 基于FPGA的光伏发电系统暂态实时仿真[J]. 电力系统自动化,2015,39(12): 13-20. [7] 李 静,蔡启仲,张 炜,等. 基于FPGA的并行操作逻辑运算控制器的设计[J]. 计算机测量与控制,2013,21(12):3380-3383. [8] 黄宇鹏,汪可友,李国杰. 基于权重数值积分的电力电子开关仿真插值算法[J]. 电网技术,2015,39(1): 150-155. [9] 舒德兀,张春朋,姜齐荣,等. 电力电子仿真中开关时刻自校正插值算法[J]. 电网技术,2016,40(5): 1455-1461. FPGA-based Simulation of Power Electronic Converter Yu Fei, Liu Yanzhi (College of Automation &Electronic Engineering, Qingdao University of Science &Technology, Qingdao 266042,China) In the field of power electronics simulation based on field programmable gate array (FPGA), the system model is usually modeling more convenient in order to achieve real-time simulation using FPGA’s characteristics of high-speed parallel computing. In this paper, establish complex model and algorithm research of boost converter based on FPGA. Based on this idea, the boost converter is modeled and studied firstly. Secondly, the boost converter is modeled based on XILINX ML605 Evaluation Kit and simulated and then the simulation waveform is compared with the waveform based on MATLAB. Form the simulation result, it can be seen the efficiency and accuracy of complex modeling and simulation of the boost converter based on FPGA. boost converter; FPGA; mathematical model; Runge-Kutta 2017-01-19; 2017-02-27。 于 飞(1961-),男,河南郑州人,教授,研究生导师,主要从事电力电子技术、智能控制方向的研究。 1671-4598(2017)08-0135-04 10.16526/j.cnki.11-4762/tp.2017.08.035 TP32 A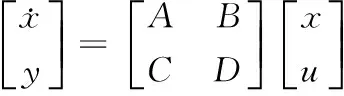
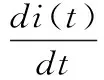
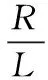
2 FPGA仿真系统设计
2.1 FPGA仿真环境和计算时序
2.2 基于FPGA的模型设计
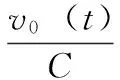
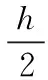
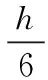
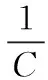
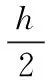
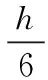
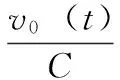
3 仿真结果
4 结论

