基于滑模控制的室内移动机器人路径跟踪
郝存明,张英坤,梁献霞
(1.河北省科学院 应用数学研究所,石家庄 050081; 2.河北科技大学 电气工程学院,石家庄 050018)
基于滑模控制的室内移动机器人路径跟踪
郝存明1,张英坤1,梁献霞2
(1.河北省科学院 应用数学研究所,石家庄 050081; 2.河北科技大学 电气工程学院,石家庄 050018)
由于轮式移动机器人的运动受限性质,其轨迹跟踪成为控制领域的研究热点;Pioneer3-AT是一个高度灵活的差分驱动的机器人,具有良好的通用性和可靠性,特别适合于移动机器人学术研究;为解决一种可以在室内环境下执行任务的移动机器人的路径跟踪问题,以Pioneer3—AT移动机器人平台为原型机建立了移动机器人的数学模型;滑模变结构控制对被控系统的不确定性、外界扰动及参数摄动具有完全鲁棒性,利用特殊幂次函数构造一种新型滑模控制趋近律,采用该趋近律设计滑模控制律,进而提出一种新的滑模控制方法,利用李雅普诺夫定理证明了该方法的稳定性;采用所设计的滑模控制器对室内移动机器人进行路径跟踪实验,仿真结果验证了该方法的有效性。
滑模控制;移动机器人;路径跟踪;趋近律
0 引言
随着人工智能技术的快速发展,机器人技术也在逐步深入和细化。移动机器人[1-4]是一个集环境感知、动态规划和决策、行为控制和执行等多种功能于一体的综合系统。由于其系统构成的复杂性,已经成为机器人技术的重要研究领域,研究者对其越来越关注。移动机器人按照工作环境可以分类为:室内移动机器人、室外移动机器人。它们都具有控制灵活、结构简单、运动性能好等优点,能够在复杂室内外环境下自组织、自规划、自适应地进行工作。进入21世纪以来,随着科学技术向前不断发展,移动机器人的应用范围也越来越广泛,在工农业生产、空间探测、医疗服务乃至城市安全、军事应用等各个领域产生了巨大的经济效益和社会效益。
移动机器人的研究涉及计算机技术、信号处理技术、机械加工技术、多传感器信息融合技术、自动控制、人工智能等诸多学科领域,代表机、光、电一体化的最高成就,是当前科学技术发展非常活跃的领域之一。对移动机器人的智能控制研究是近年来机器人控制领域的前沿课题,主要关注模型设计、定位方法、控制稳定性和路径规划等方面的问题。普遍采用基于机器人几何中心或轮轴线中心的时间微分方程的运动学模型进行建模。采用动态定位方法,将外部传感器获得的信息与推算信息进行融合,以获取高精度定位。利用具有高容错能力智能算法调节控制律中的参数,增强系统对参数扰动的鲁棒性。为达到移动机器人能够按照预先给定的任务指令,根据已有的地理信息作出理想的路径规划,并在前进的过程中不断感知周围环境,作出决策引导,并执行给定的任务指令。这些相关的研究工作已经取得了相当丰富的研究成果,而移动机器人路径跟踪问题[5-7]的研究也已成为国内外研究的热点之一。李林琛等[8]将遗传算法和PID控制相结合用来解决移动机器人的轨迹跟踪问题,利用遗传算法对PID参数进行在线整定和优化,从而降低了跟踪误差。孙晓燕[9]研究了不同环境和任务下欠驱动水下机器人的路径跟踪,设计了一种模糊PID控制应用于机器人的艏向控制。贾鹤鸣等[10]设计基于反馈增益的反步法控制器,采用神经网络对模型不确定项进行补偿,并利用自适应鲁棒控制器在线补偿神经网络的估计误差,实现移动机器人对任意曲线路径的精确跟踪。邓学强[11]为解决移动机器人在路径跟踪任务中目标不可达问题,提出一种新的斥力改进函数,将其成功应用于移动机器人的局部路径规划。
移动机器人系统是一个多输入多输出的复杂系统,具有时变性、耦合性、非线性和不确定性。滑模变结构控制[12-15]对被控系统的不确定性、外界扰动及参数摄动具有完全鲁棒性,因此滑模变结构控制适用于解决移动机器人的轨迹跟踪问题。但是滑模变结构控制也存在不足,当系统状态到达滑模面后,会在滑模面附近产生高频震荡,即“滑模抖振”,在一定程度上制约其发展。本文从控制策略角度考虑,提出一种基于新型趋近律的滑模控制算法,通过采用这种控制方法使得室内环境下移动机器人的行走轨迹能够跟随理想轨迹,且不会产生较大偏差。
1 移动机器人结构及运动学分析
1.1 Pioneer3-AT系统结构
本文采用的实验平台为美国ActivMedia Robotics公司研制的一个标准的智能移动平台:Pioneer3-AT移动机器人。该机器人平台是一款多用途、四轮驱动机器人平台,具有较高的输出扭矩,安装的是带有花纹突起的室外胎,能在各种粗糙路面环境下的室内外项目中应用。该机器人工作模式有服务器模式、自检模式、操纵杆驱动模式和维护四种,在服务器工作模式下,上位机通过串口和下位机通信,获取下位机读取的数据并对数据进行处理,然后发送控制命令给下位机,由下位机负责电机的控制实现机器人移动;自检工作模式主要是测试平台电机性能指标用。在操纵杆驱动模式下,可利用操纵杆驱动机器人,不用连接客户端计算机。维护模式下,用户可根据需求通过直接修改FLASH内的程序控制机器人移动。此外该平台采用日立公司的H8S微控制器作为下位机,PC104中央处理器作为上位机,具有更快捷的处理速度和更加强大的扩展能力,能够支持用户对基于以太网的通讯系统、车载视觉处理系统、DGPS、激光扫描仪及其他功能设备的扩展。
Pioneer3-AT移动机器人其本体结构如图1所示,主要由传感系统、控制系统和运动系统组成。Pioneer3-AT由4个轮子支撑,其中前2个为驱动轮,同侧两轮通过铰链连接实现共速。机器人采用四轮差分驱动,底部装有4个高速、高转矩、可逆转直流电机,每个电机都装有高分辨率增量式光学编码器,通过差分控制方式对驱动轮进行驱动,根据左右两侧车轮的速度差实现机器人的转向运动。
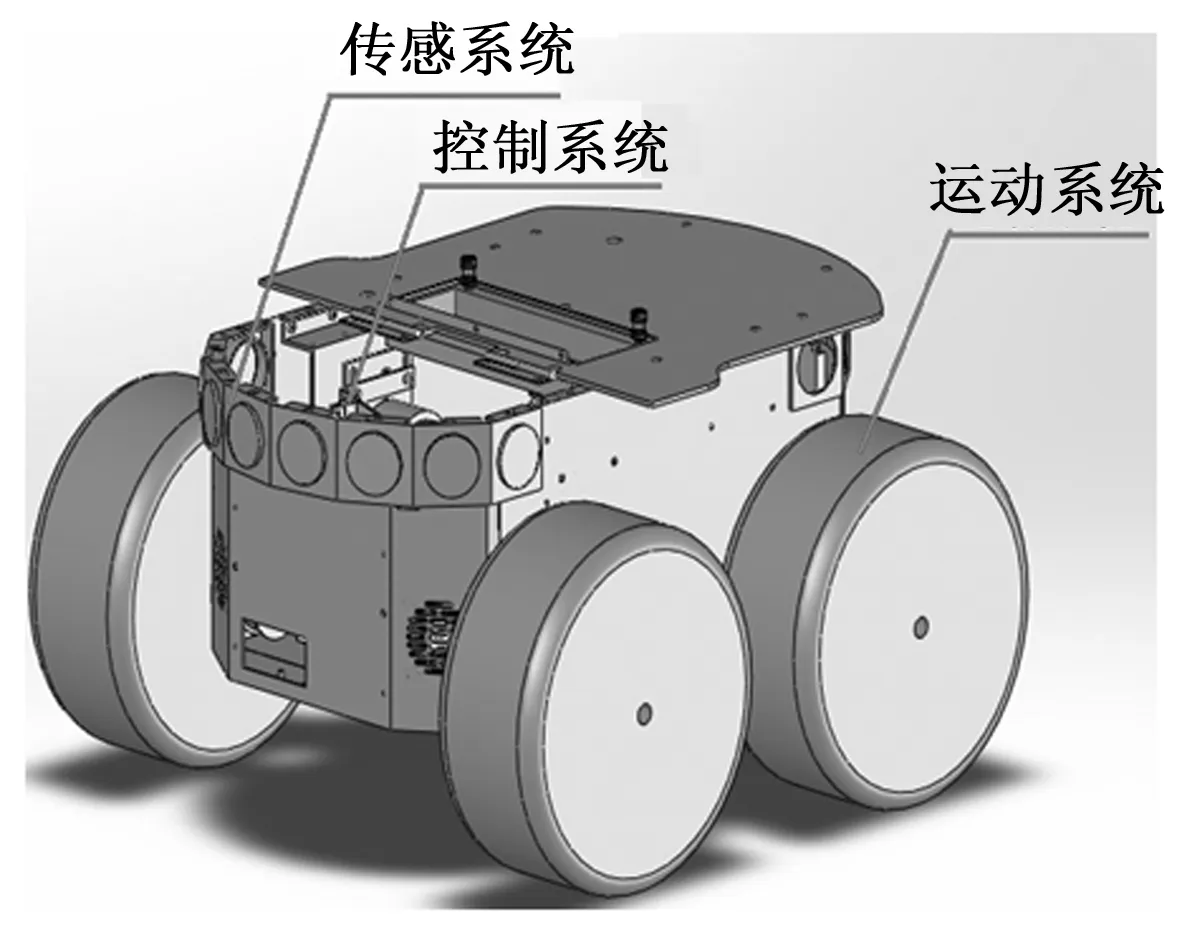
图1 Pioneer3-AT移动机器人本体结构图
1.2 移动机器人运动学建模
对Pioneer3-AT移动机器人系统进行运动学分析,在平面坐标系下建立如图2所示的移动机器人模型。移动机器人的四个轮都是驱动轮,分别由四台电机驱动。在工作过程中,通过调整四个电机的输入电压来调节四轮是转速。在整个运动学分析过程中,我们将机器人建模成轮子上的一个刚体,运行在水平面上。为了确定机器人在平面中的位置和姿态,我们建立了机器人平面坐标系。选取移动机器人底盘上的中心点O为参考点,并定义移动机器人的位姿信息为(x,y,θ),其中x,y为移动机器人中心点在坐标系下的位置坐标,θ为机器人移动方向与X轴正方向的夹角。vL,vR分别为机器人左、右两侧驱动轮的线速度,ωL,ωR为机器人左、右两侧驱动轮的转动角速度,2L为左右两侧驱动轮间的轴间距,R为车轮半径。
移动机器人的线速度v和角速度ω的关系为:
(1)
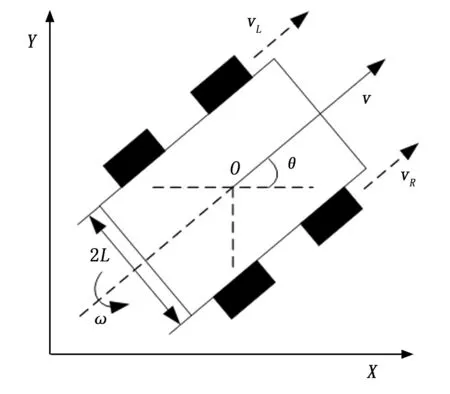
图2 移动机器人模型示意图
移动机器人移动方式属于刚体运动,机器人各点以相同角速度绕中心转动,易得移动机器人的运动学微分方程为:
(2)
将(2)式表达为矩阵形式则为:
(3)
2 电机的数学模型
为实现Pioneer3-AT移动机器人轨迹跟踪的控制,我们需要设计电机控制方法,使得电机能够响应移动机器人的速度指令。本文通过改变移动机器人的角速度和线速度来实现对移动机器人的轨迹跟踪控制,由机器人内部的运动控制卡实时获取电机编码器的数据控制机器人运动,并调用本文所设计滑模控制算法进行移动机器人轨迹跟踪控制。
直流电机的工作原理是:给电枢绕组施加直流电压,使带电的电枢绕组在磁场的作用下产生电磁力,形成旋转的电磁转矩,从而驱动电机转子的转动。
忽略直流电机上的各种干扰,不考虑电枢反应,忽略磁路饱和,忽略齿槽效应,不计涡流和磁滞损耗。将直流电机驱动器设置为速度控制模式,建立各支路电机的数学模型。
电机的电压平衡方程为:
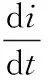
(4)
式中,u为定子相电压,R为相电阻,i为定子绕组相电流,L为定子电感,ε为反电动势。
根据电磁力定律,当电枢绕组有电枢电流流过时,在磁场内将受到电磁力的作用,该力与电机电枢铁芯半径的乘积为电磁转矩。考虑空载情况,此时电磁转矩方程为:
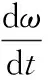
(5)
式中,Te为电磁转矩,J为转动惯量,ω为角速度,kT为转矩系数。
由电磁感应定律可得直流电机绕组的动态方程为:
ε=kεω
(6)
式中,kε为反电动势系数。
由式(4)~(6),可得直流电机动力学系统方程为:
(7)
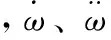
对式(7)进行拉普拉斯变化并整理,得直流电机的传递函数为:
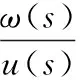
(8)
3 滑模控制器设计
滑模控制理论是一种特殊的非线性控制理论,其基本思想是:系统由若干个具有不同参数或结构的子系统组成,工作时根据某种函数规则在子系统间进行切换,从而改善整个系统的动态性能。其主要优点是响应速度快,对系统参数变化不敏感,对未建模动态和外部干扰有良好的适应能力。滑模控制方法通过对控制量进行切换来使系统状态沿着滑模面滑动,且在滑动模态时对匹配摄动和外干扰具有不变性,因此可用来对复杂的移动机器人系统设计控制律。
3.1 利用特殊幂次函数构造新型趋近律
在滑模控制中,传统趋近律存在抖动严重、收敛速度慢、收敛时间长等缺点,用幂次函数构造趋近律能够使得状态在接近滑动模态时趋近的速度放缓,这样可以大大减弱抖动,但是系统在远离滑动模态时的趋近的速度过小,导致运动时间过长。为弥补幂次趋近律这一不足,本文基于一种特殊的幂次函数,提出一种新型滑模控制趋近律:
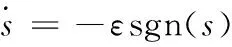
ϑ(s)-ks
(9)
式中,ε>0,k>0。
其中,函数ϑ(x)的表达式为:
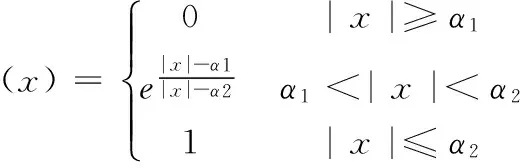
(10)
其中:α1,α2为阈值,根据实际系统确定,且,0<α1<α2。
ϑ(x)在原点附近为光滑连续函数,从而能保证系统状态平滑的进入滑模面,可以有效抑制抖振的不利影响。指数趋近项ks可以使趋近速度从较大值逐步减小到0,保证了系统状态以较大的速度趋近滑动模态,缩短趋近时间。
3.2 控制律设计
完整的滑模运动包含趋近运动和滑模运动两部分。滑模控制的可达性条件只能保证在状态空间内,任意位置的运动点在有限的时间内到达切换面,但是对于趋近轨迹没有作任何限制。为了改善系统的动态品质,一般采用趋近律的方法来设计滑模控制器。
针对本文所研究的室内移动机器人,以下是采用我们设计的新型趋近律来设计的机器人运动的控制律。
推荐理由:《敬人书语》是设计大师吕敬人先生经过多年学习、创作和教育实践积累而写就的系统性设计之书。本书分为书艺问道、对话、人物谈、创作谈、书评、写序、教学等部分。以设计范式的转变,即由装帧向编辑设计的转变为线索,理清了书籍设计方方面面的历史流变,展现了东方传统文化的魅力所在,揭示了书籍设计的本质。
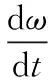
(11)
式中,d(t)为系统内部和外部扰动作用的总和,且有界。
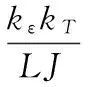
(12)
取滑模函数为:
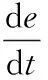
(13)
其中,e=x1-ωd为系统误差,c>0,满足Hurwitz稳定条件。
对式(13)求导可得:
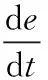
(14)
结合式(10)的趋近律可得控制律为:
(15)
3.3 稳定性分析
构建控制器之后需要对移动机器人控制的稳定性进行分析,首先,判断该控制器的设计是否满足了控制器设计的最基本的准则—系统稳定性,如果控制器设计得不合理,系统将会发生不稳定现象,系统误差将不是减小,而是放大,那么将导致后面的仿真实验和实物验证实验的失败。因此,分析控制器的稳定性是十分有必要。机器人系统稳定是指机器人在实现所规定的运动轨迹时,即使在一定的干扰作用下,其误差仍然保持在很小的范围之内。
目前,研究移动机器人等非线性不确定性系统稳定性的有效方法仍然是李雅普诺夫稳定性理论。利用这种理论分析系统的稳定性,并不需要求解系统的运动方程来考察状态的具体动向,而只需寻找或构造一个被称为李雅普诺夫函数的正定函数,并考察其沿状态轨迹的时间微分。
定义李雅普诺夫函数:

(16)
对V求导可得:
s(-εsgn(s)ϑ(s)-ks)=
-εssgn(s)ϑ(s)-ks2≤0
(17)
由式(16)和式(17)可判定系统稳定。
4 仿真实验与分析
4.1 系统仿真
在MATLAB环境中对移动机器人控制系统进行仿真,探讨本文所提出控制算法的有效性。
仿真所用移动机器人的电机参数为:P0=0.2 kW,n0=3 000 r/min,U0=12 V,R=0.64 Ω,I0=1.5 A,L=10 mH,Kε=0.037/(rad/s),J=0.06 g·m2,KT=0.035 N·m/A。
控制器参数选取:c=5,k=0.8,ε=10。
白噪声干扰为:d(t)=50*rand(1,1)。
将各参数代入式(8)可得直流电机的传递函数为:
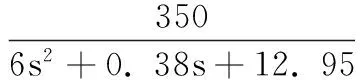
(18)
仿真结果如图3~图5,图3为位置跟踪曲线,图4为速度跟踪曲线,图5为趋近律的相轨迹。
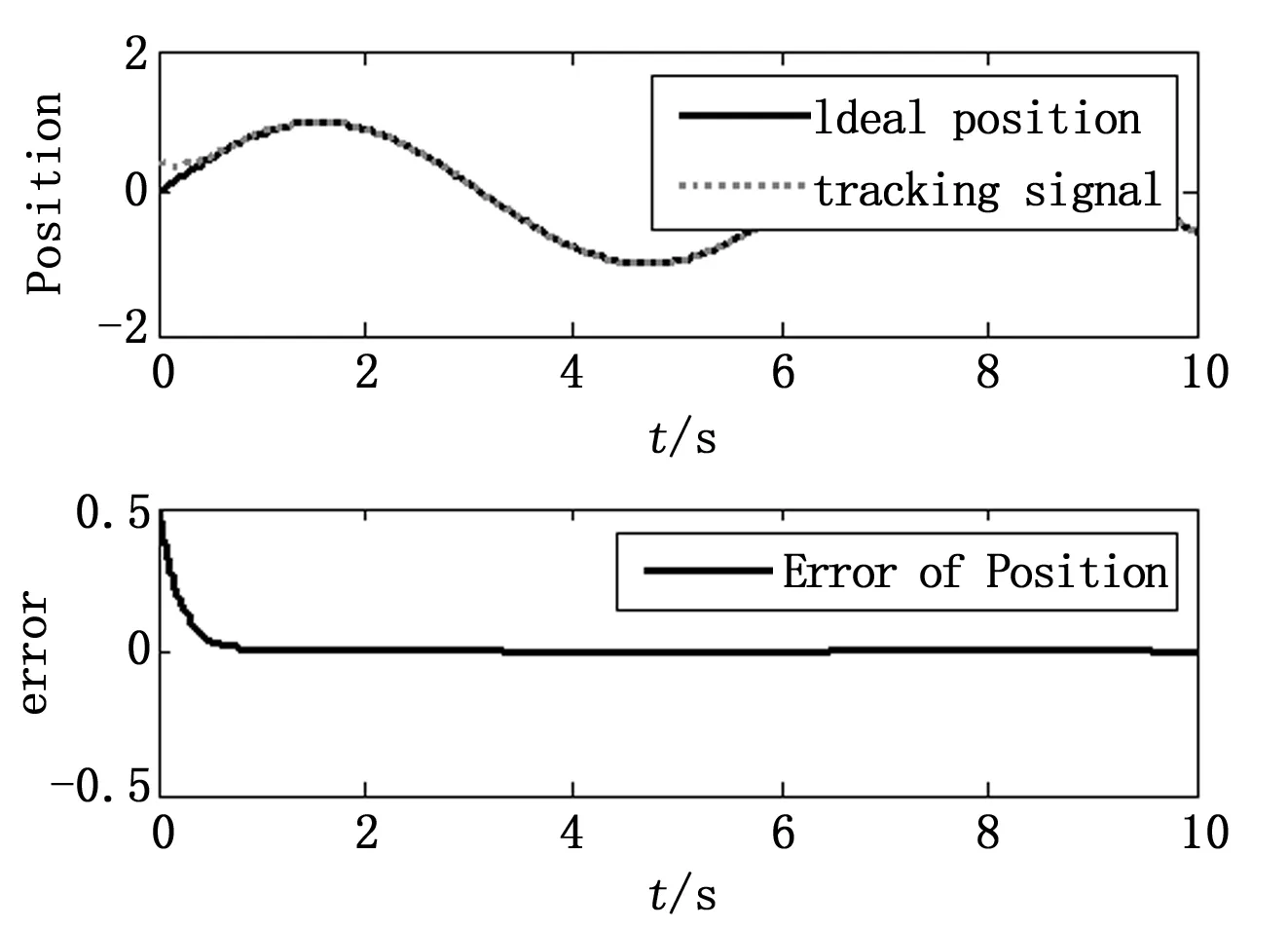
图3 位置跟踪曲线
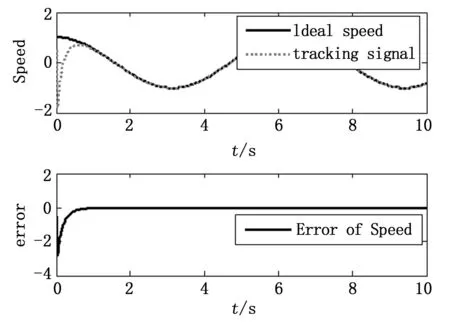
图4 速度跟踪曲线
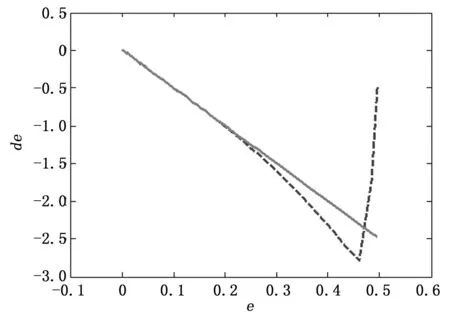
图5 趋近律的相轨迹
由图3和图4可知,采用本文所设计趋近律的滑模控制器,移动机器人的位置跟踪精度和速度跟踪精度都较高,位置跟踪误差和速度跟踪误差较小,且收敛速度较快。从图5可以看出,系统在完成切换进入稳态后逐渐趋近于原点,不存在大幅度的抖振,达到很好的控制效果。
4.2 存在的不足
本文仅在Simulink环境下进行了移动机器人的仿真实验,缩短了控制算法验证的时间,但是也存在一些不足:
1)实现移动机器人的路径跟踪有许多算法,根据实际要求不同,算法的性能也不同,本文对同等条件下不同算法的对比有待研究。
2)本文侧重于仿真,但是仿真环境与实际的真实环境存在差距,仿真实验并不能完全等同于实际测试。
5 结论
本文针对室内移动机器人的路径跟踪问题提出了一种新的滑模控制方法,设计了一种新型滑模控制趋近律,在此基础上设计滑模控制器,并利用李雅普诺夫定理证明了该滑模控制系统渐进收敛。仿真实验表明,在考虑移动机器人系统参数变化和外界干扰等的情况下,采用该滑模控制律的移动机器人系统具有较高的位置跟踪和速度跟踪精度,并有效的抑制了抖振现象,实现了路径跟踪的快速性和精确性。
后续工作一方面是用本方法和其他移动机器人的路径跟踪算法进行对比;另一面是将本文提出的滑模控制方法在Pioneer3-AT移动机器人系统中进行实验研究,在实际环境中评测本文方法在移动机器人路径跟踪中的性能。
[1] 陈顺立.农业机器人路径优化及轨迹跟踪研究-基于遗传算法[J].农机化研究,2017(8):17-22.
[2] Zeng W, Wang Q H,Fenglin Liu,Ying Wang.Learning from adaptive neural network output feedback control of a unicycle-type mobile robot[J].ISA Transactions,2016,16:337-347.
[3] 黄铝文.苹果采摘机器人视觉识别与路径规划方法研究[D].杨凌:西北农林科技大学,2013.
[4] 栾禄祥.室内移动机器人机器视觉定位系统的设计[J].自动化仪表,2017,38(2):49-52.
[5] 黄轶文,张梅.基于蚁群算法的六自由度采摘机器人轨迹规划研究[J].农机化研究,2017(3):242-246.
[6] 黄立新,耿以才.基于动态人工势场法移动机器人路径规划研究[J].计算机测量与控制,2017,25(2):164-166.
[7] 高 慧.基于强化学习的移动机器人路径规划研究[D].西南交通大学,2016.
[8] 李林琛,蒋小平.基于PID控制的移动机器人路径跟踪[J].激光杂志,2016,37(2):110-112.
[9] 孙晓燕.基于模糊PID的欠驱动水下机器人路径跟踪方法研究[J].制造业自动化,2015,37(4):145-148.
[10] 贾鹤鸣,宋文龙,陈子印,等.基于神经网络反步法的移动机器人路径跟踪控制[J].南京理工大学学报,2014,38(1):27-33.
[11] 邓学强.基于改进人工势场法的移动机器人路径规划[J].山东理工大学学报(自然科学版),2014,28(1):38-41.
[12] 李慧洁,蔡远利.基于双幂次趋近律的滑模控制方法[J].控制与决策,2016,31(3):498-502.
[13] 唐传胜,李忠敏,李 超.基于干扰补偿的不确定机器人鲁棒滑模跟踪控制[J].组合机床与自动化加工技术,2016(7):99-104.
[14] 王艳敏,冯 勇,夏红伟,等.多输入不确定系统的平滑非奇异终端滑模控制[J].控制与决策,2015,30(1):161-165.
[15] 刘永慧.不确定切换系统的滑模控制方法研究[D].华东理工大学,2014.
Path Tracking of Indoor Mobile Robot Based on Sliding Mode Control
Hao Cunming2, Zhang Yingkun2, Liang Xianxia2
(Institute of Applied Mathematics, Hebei Academy of Sciences, Shijiazhuang 050081, China)
Due to the restricted mobility, the trajectory tracking of wheeled mobile robot, has been a research focus in the field of control. The Pioneer3-AT is highly versatile differential-drive robotic platform for academic researchers,which has the most famous advantages of good versatility and reliability.To solve the path tracking problem of the indoor mobile robot which can perform particular tasks, the mathematical model of the mobile robot is established. based on Pioneer3—AT. Sliding mode variable structure control for the uncertainty, external disturbance and parameter perturbation of the controlled system has completely robustness, and a new sliding mode reaching law with special exponential function is constructed. The reaching law is adopted to design the sliding mode control law, and put forward a new method of sliding mode control is proposed, and the method stability.is proved by using lyapunov theorem.The simulation results of the indoor mobile robot path tracking experiment on the sliding mode controller demonstrate the effectiveness of the proposed method.
Sliding mode control;Mobile robot;Path tracking;Reaching law
2017-04-11;
2017-04-27。
河北省科学院科技计划项目(14605)。
郝存明(1981-),男,河北宣化人,硕士,助理研究员,主要从事应用数学方向的研究。
1671-4598(2017)08-0093-04
10.16526/j.cnki.11-4762/tp.2017.08.024
TH16
A

