基于SkipGram模型的链路预测方法

赵 超 朱福喜,2 刘世超

1(武汉大学计算机学院 湖北 武汉 430072)

2(汉口学院计算机科学与技术学院 湖北 武汉 430212)

基于SkipGram模型的链路预测方法

赵 超1朱福喜1,2刘世超1

1(武汉大学计算机学院 湖北 武汉 430072)

2(汉口学院计算机科学与技术学院 湖北 武汉 430212)

现有的基于节点相似性的链路预测算法，在提升预测准确度时往往无法兼顾计算复杂度。受自然语言概率图模型在词向量表征上的运用启发，提出一种基于SkipGram模型的链路预测方法。首先提出基于概率的随机游走方法，通过这种方法得到网络节点的采样序列；然后结合SkipGram模型将网络节点映射到一个低维向量空间来降低复杂度；最终以向量间的距离作为衡量网络节点间相似性的指标，进而完成链路预测。通过在6个具有代表性的真实网络中进行实验和比较发现，提出的模型在预测准确度上得到大幅提高。

链路预测 向量表征 SkipGram模型 节点相似性

0 引 言

现实生活中许多复杂的系统都能够使用网络来描述，网络中的节点即代表系统中的个体，节点间的连边代表个体间的相互关系。因而，复杂网络逐渐成为分析一个复杂系统的重要工具。链路预测作为社会网络(复杂网络之一)研究中的一个重要分支，受到了来自各个领域的学者的关注。例如，蛋白质相互作用网络[1]、科学合作网络[2]、社交网络[3]等都是研究的热点方向。

链路预测即利用网络中已知的节点信息来预测网络中尚未产生连边的节点之间产生连边的可能性。如图1所示，链路预测即利用图1(a)中的已知节点信息，来预测图1(b)中虚线连边产生的概率。链路预测有两个方面的含义，一是预测网络中已经产生但还未被发现的连边，二是预测网络中目前还未产生但将来可能产生的连边。

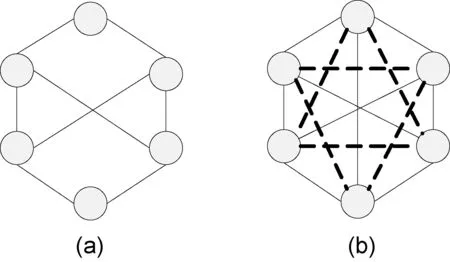
图1 链路预测问题描述图

链路预测的传统做法一般是基于机器学习和马尔科夫链的，如文献[4]使用马尔科夫链来进行自适应网络中的链路预测；文献[5]使用马尔科夫链来进行链路预测和网络中的路径分析。此类基于传统机器学习的链路预测方法多半利用了网络中节点的属性信息，然而节点的属性信息既难以获取且无法保证其可靠性。例如，在目前十分流行的社交网站中，用户填写的个人信息一定程度上是虚假的，因而以此构建社交网络并进行链路预测，其结果必然是不可靠的。

由于利用网络中节点属性进行链路预测存在诸多弊端，基于网络节点相似性的算法得以发展。文献[6]基于“度小的共同邻居贡献大于度大的共同邻居”的认知提出了AA算法；文献[7]从网络中资源分配的角度出发提出了RA算法。基于网络全局相似性的算法往往计算复杂度过高，根本无法在较大规模的网络中使用；基于网络局部相似性的算法虽然降低了计算复杂度，然而代价却是预测效果的相对下降。

近年来，深度学习逐渐成为一个热门研究方向，它在音频处理、图像处理以及自然语言处理等领域的成功运用为解决链路预测问题带来了启示。文献[8]提出了一种神经概率语言模型，运用人工神经网络来学习一种分布式表征的词向量，解决了统计语言模型中常见的维数灾难问题，同时使得向量间的相互运算变得有意义。文献[9]提出了CBOW模型和SkipGram模型，用以大规模文本连续性表达的学习。

本文受自然语言概率图模型在词向量表征上的应用启发，提出一种基于SkipGram模型的链路预测方法。通过基于概率的随机游走得到网络中的节点序列，结合SkipGram模型训练得到节点对应的向量，利用节点向量间的距离来衡量对应节点间的相似度，以此相似性指标来进行链路预测。经过在6个真实的网络中进行实验和比较发现，本文提出的模型相比基准算法而言，在预测准确度上有较大的提升。

1 相关工作

迄今为止，绝大多数的链路预测算法都是基于节点相似性定义设计的。一类是基于节点属性的相似性指标，如果两个节点拥有的共同特征越多[10]，则这两个节点越相似；另一类节点相似性指标完全是基于网络结构的，称为结构相似性指标。结构相似性指标可以划分为基于节点、基于路径和混合方法三种类型。文献[5]对上述3种类型的指标进行了比较，共同邻居(CN)[11]、Jaccard系数[12]、AA指标[6]和PA指标[13]都被归为基于节点的标准；而Katz指标[14]、命中次数[15]、往返次数[16]、PageRank[17]、SimRank[18]和Blondel指数[19]都被归为基于路径的标准。此外，Leicht等[20]基于假设——如果网络中两个节点的邻居相似，则这两个节点相似，提出了一种量化节点相似性的方法，这种相似性指标可以作为一种候选的精确链路预测方法。

除了基于相似性的链路预测算法之外，近年来一些更为复杂的算法也逐步被提出。Clauset等[21-22]基于层次网络结构提出一种链接预测算法，首先使用一个层级随机图来近似真实的网络数据；随后根据横向链接概率的深度推断出节点的层次结构；最后通过降序排列横向链接概率预测网络中的缺失链接。此外，研究人员也做了大量的工作来设计推荐系统[23]。事实上，向用户推荐产品的过程可以看作是预测用户-商品二分图中缺失链接的过程[24]。值得一提的是，基于能量传播[25]和热传导[26]理论，物理学家近来提出了一些信息推荐算法。尽管相关问题还没有被全面探索过，然而运用经典的物理理论仍有可能增加链路预测算法准确度。

链路预测的研究仍然面临着许多难题，其一就是目标网络的稀疏性问题[27]。稀疏网络中存在大量的孤立节点，导致建立合适的统计模型变得非常困难。另一个问题就是真实网络往往过于庞大，对算法的效率要求非常高。一般而言，链路预测算法的准确度与其计算复杂度是呈正相关的，准确度越高通常意味着更高的计算复杂度。

2 模型和算法

本文提出的模型(如图2所示)主要包含两个过程：(1) 使用基于概率的随机游走获取网络中的节点序列；(2) 利用SkipGram模型训练节点对应的向量。在获取网络中节点对应的向量之后，采用余弦相似性来度量向量间的距离，进而间接衡量对应节点间的相似度，进行链路预测。

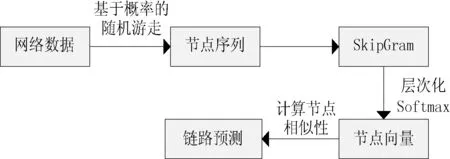
图2 模型流程图

2.1 基于概率的随机游走

文献[28]所提出的模型第一步就是使用随机游走来对网络节点进行序列化，随机游走实际上也是一种概率游走，只不过它在当前位置选择下一步都是等概率的。序列化的节点就相当于语言模型中的句子，大量的句子就构成了语料库。很显然，不论是一般的随机游走还是基于概率的随机游走，其要求都是所得到的节点序列要能正确反映出网络的结构特征。

网络中的随机游走在当前节点选择下一个节点时都是等概率的，这也就意味着对于目标节点的邻居节点，随机游走时认为它们都是一样的。然而事实并非如此，目标节点的多个邻居节点之间必然是存在差异的。例如在一个无标度图中，度大的节点之间和度小的节点之间未来产生连边的概率前者要明显大于后者，倘若使用随机游走对网络进行采样，则不免最终结果弱化了度大节点的作用，节点序列也就无法准确地反映网络的特征。

基于随机游走对网络节点进行采样的不足，本文提出基于概率的随机游走(简称PBWalk)来对无向无权网络中的节点进行序列化。基于概率的随机游走根据当前节点与邻居节点的共同邻居数目来为邻居节点赋予权值：各邻居节点权值均初始化为1，和当前节点间每增加一个共同邻居，权值加1。基于概率的随机游走计算从当前节点转移到各邻居节点的概率为：

(1)

其中x表示游走的当前节点，Γ(x)表示节点x的邻居集合，Sx表示节点x的各邻居节点的权值总和，即：

(2)

如图3所示，假设在网络中进行游走的当前节点为A，则需要从节点A的邻居节点B、C、D和F中选择一个作为游走的下一步，图3中(a)和(b)分别显示了随机游走和基于概率的随机游走从节点A到邻居节点的转移概率。随机游走选择邻居的概率都相同，因而图3(a)从A转移到B、C、D和F中任何一个节点的概率都是1/4；基于概率的随机游走选择邻居是依据共同邻居数目来加权选择，根据式(1)计算可知，A转移到节点C、D和F的概率要大于转移到节点B的概率。

图3 随机游走与基于概率的随机游走对比

利用基于概率的随机游走获取了网络的节点序列之后，将这些节点序列作为SkipGram模型的输入，利用SkipGram模型训练得到节点对应的词向量。

2.2 SkipGram

SkipGram是一个神经概率语言模型，它使用一个单词来预测句子而不是使用句子上下文来预测缺失的单词。句子的上下文由给定单词左边和右边出现的单词组成。SkipGram语言模型要求极大化单词出现在上下文中的概率，优化的目标函数形式如下：

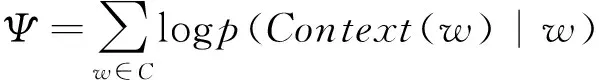
(3)

其中w表示当前词，Context(w)表示词w的上下文，C表示语料库。SkipGram将条件概率函数p(Context(w)|w)记为如下形式：

(4)

2.3 目标函数求解

SkipGram模型的输出对应一棵Huffman树，该树是根据网络节点在概率游走节点序列集中出现的频次构造的，树的叶子节点对应网络中的节点。对于网络中的任意节点，Huffman树中必存在一条从根节点到该节点对应叶子的路径，可以将路径上的每一个分支看作一次二分类，每一次分类就产生一个概率，将这些概率相乘就得到所求的p(Context(w)|w)。

运用逻辑回归进行二分类，式(4)中的p(u|w)可以表示成如下形式：

(5)

(6)

综合式(3)-式(6)即可得到目标函数Ψ：

(7)

其中：

φ(w,u,j) =φ(w,u,j)1+φ(w,u,j)2

使用随机梯度上升对目标函数进行优化，v(w)的更新公式可以表示为：

(8)

其中η表示学习率。

本文模型对应的算法如下：

输入： 图G(V,E)

节点上下文窗口w

节点向量维数d

概率游走总次数r

概率游走长度t

输出：节点向量矩阵Φ

1 for i = 0 to r do

2 O = shuffle(V)

3 for each vi∈O do

4Wvi= PBWalk(G,vi,t)

5 SkipGram(Φ,Wvi,w)

6 end for

7 end for

2.4 使用节点向量进行链路预测

利用基于概率的随机游走算法对网络中的节点进行序列化，然后使用SkipGram语言模型结合神经网络训练得到网络中节点对应的词向量vj，就可以将计算网络中节点间相似性的问题转化为计算节点对应的词向量间的距离问题。为了尽量降低算法的时间复杂度，选择较为通用的余弦相似性算法来计算网络中节点间的相似度：

(9)

在得到网络中所有节点对应的词向量后，使用式(9)可以计算出测试集中所有节点间的相似性分数，将相似性分数降序排列成一个列表，取前若干个分数值对应的连边和测试集进行比较，得到这些边出现的概率。

3 实验和结果分析

3.1 数据集

本文选取了不同领域具有代表性的6个网络：(1) 蛋白质相互作用网络(PPI)[29]——该网络包含2 617个蛋白质、11 855个相互作用关系。(2) 科学家合作网络(NS)[30]——该网络包含1 589位科学家，其中128位孤立的科学家并未纳入考虑范围。科学家合作网络的连接情况并不好，它共包含268个联通子集，其中最大的联通子集却只有379个节点。(3) 美国电力网络(Grid)[31]——网络节点代表发电机或基站，网络连边则表示连接节点间的高压线路。(4) 政治博客网络(PB)[32]——虽然原始网络是有向的，但是本文实验将其视为无向网络。(5) 路由器网络(INT)[33]。(6) 美国航空网络(USAir)[34]——该网络表示美国航空运输系统，包含有332个机场、2 126条航线。

表1总结了上述6个网络的拓扑性质，其中N和M分别代表网络中的节点数和边数；Nc表示网络中最大联通子集的规模，例如PPI网络包含92个联通子集，最大联通子集包含2 375个节点；C和d分别表示网络的聚集系数和平均度。

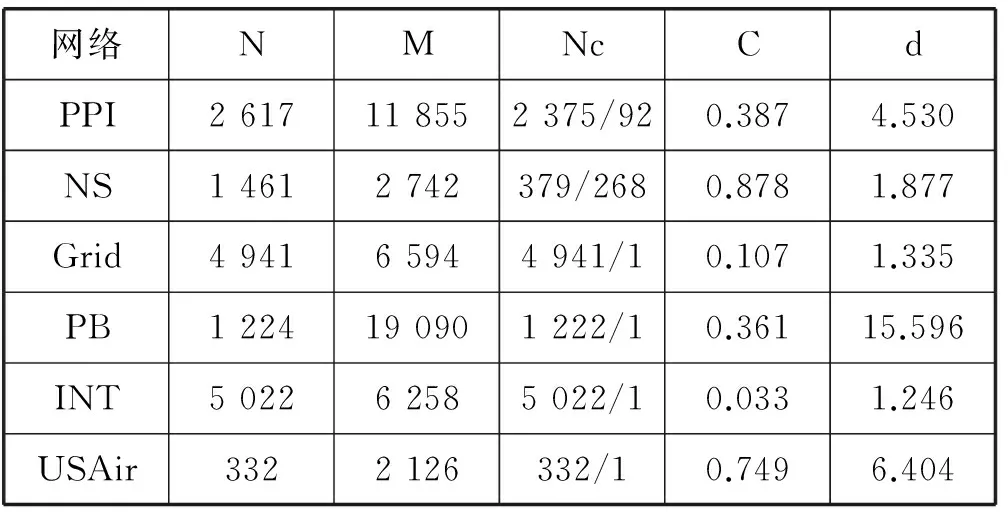
表1 实验网络的拓扑性质

3.2 评价方法

为了测试算法的准确性，将网络中已知的边集随机分为训练集ET(90%)和测试集EP(10%)两部分，且ET∪EP=U和ET∩EP=∅。在计算相似性分数的时候只能使用训练集ET中的数据。

本文采用AUC指标[35]和Precision指标[36]来对链路预测结果进行评价，AUC可以看作是随机选择的一个不存在的边比测试集中的边相似性分数小的概率。AUC计算公式可以表示为：

(10)

其中n表示测试集中的边的分数值和不存在的边的分数值独立比较的次数，n′表示n次比较中测试集中边的分数值比不存在的边分数值大的次数，n″表示n次比较中测试集中的边和不存在的边分数值相等的次数。

Precision指标将实验结果的相似性分数按降序排列成一个列表，取前L条记录，如果其中有n条记录对应的边出现在测试集中，则Precision的计算公式可以表示为：

(11)

3.3 实验结果

本文的实验结果都是在对原始数据集进行100次随机划分形成训练集和测试集，然后取实验所得数据的均值得到的。采用AUC指标和Precision指标来对实验结果进行评价，在AUC评估方法中进行了100 000次随机抽取比较，Precision取相似性分数列表的前100条记录与测试集进行比较。

已有的实验研究[3,7]证明，在基于节点结构相似性的链路预测算法中，CN、AA和RA算法通常比其他算法具有更好的预测效果。因此本文将CN、AA和RA算法作为基准对比方法，同时将文献[29]中的LsNet2Vec算法(简记LNV)也纳入对比。将本文提出的模型对应的算法简记为PW，实验结果如表2和表3所示。

表2 实验结果AUC值

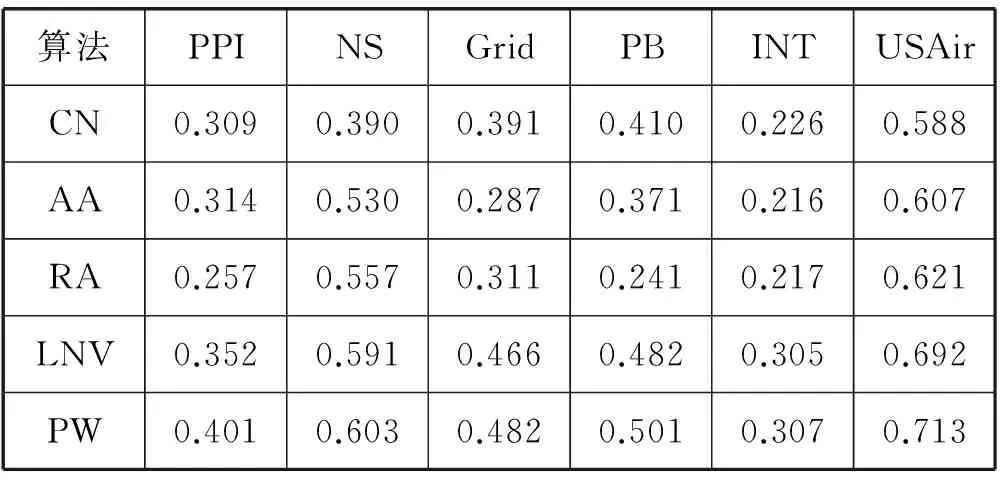
表3 实验结果Precision值

通过对表2和表3中的实验数据进行分析发现，PW算法相比传统的基于节点相似性的算法，在预测效果上都有较大的提升。尤其是对于类似INT这种网络聚集系数非常小的网络，在传统的基于节点相似性的算法都无法准确预测的情况下，使用PW算法仍能够获得较理想的链路预测结果。

PW算法相比LNV算法，实验结果AUC值和Precision值均有提升。PW算法使用基于概率的随机游走来对网络节点进行序列化，使游走得到的网络节点序列更加真实地反映了网络的拓扑结构性质，有助于在使用神经网络训练语言模型时得到更高质量的节点向量，取得更加良好的预测效果。

3.4 参数讨论

本节对模型中的两个参数游走长度和节点向量维度进行讨论。基于概率的随机游走长度默认值为20，节点向量维度默认值为50，在讨论其中一个参数时，另一个参数固定为默认值。

3.4.1 基于概率的随机游走长度

本文选择游走的长度范围为[20,120]，同时每次增加10个步长，通过实验来探讨预测结果AUC值和基于概率的随机游走长度间的关系。观察图4中曲线发现，随着游走长度的增加，各网络中预测结果的AUC值整体都是上升的，最终趋近于平稳。NS、Grid和INT网络较为稀疏，随着游走长度的增加，网络节点的采样更加充分，因而AUC值上升的速度更快；相反在较为稠密的网络如PB网络中，AUC值上升较为缓慢，因为在游走长度不是很大的情况下已经足以对网络进行充分采样了。在游走长度增大到一定程度时，网络信息已经被充分获取，继续增大游走长度不能继续提升AUC值。

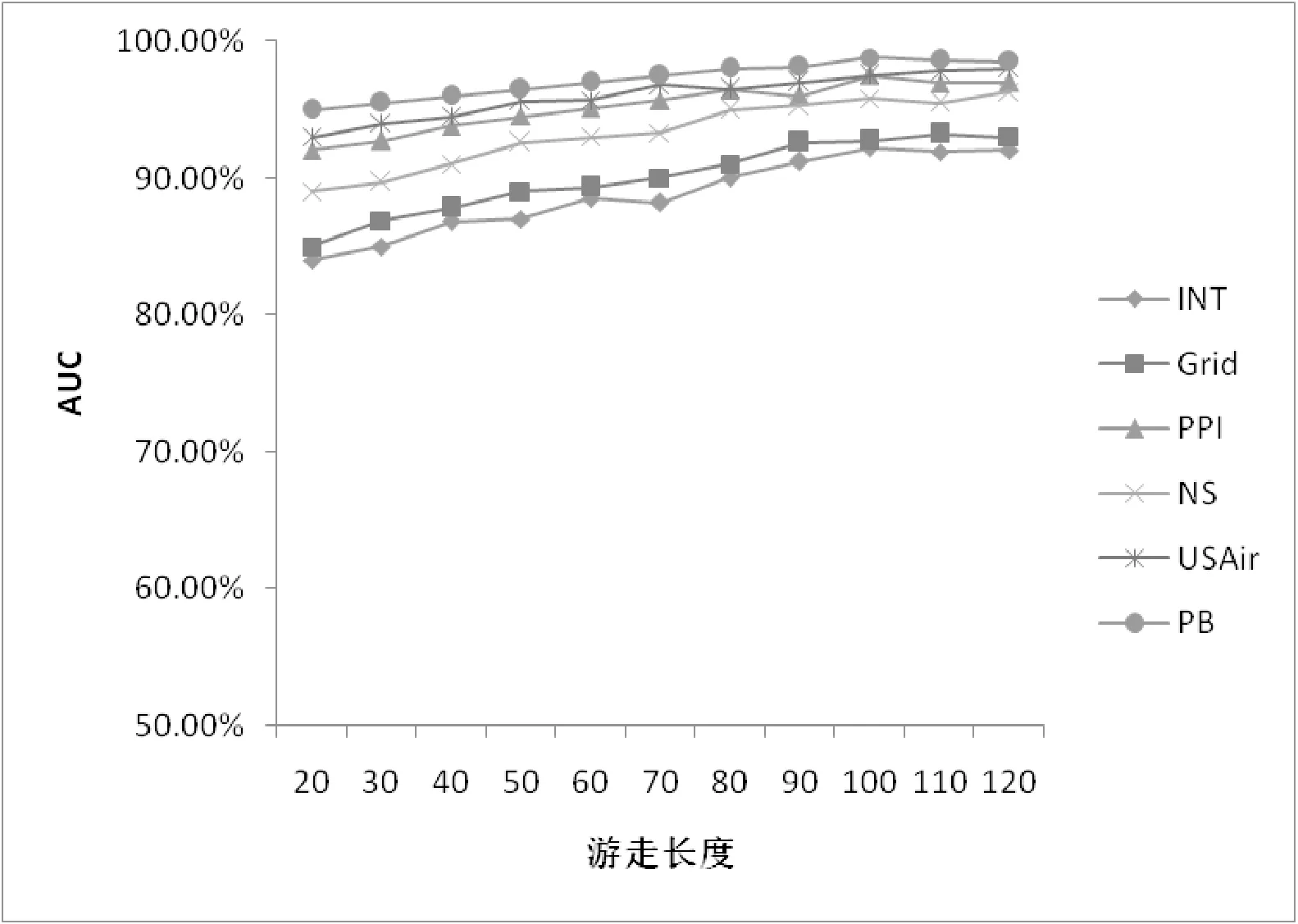
图4 游走长度与AUC关系

3.4.2 节点向量维度

本文选择节点向量维度的变化范围为[50,200]，每次增加25个维度数，通过实验来探讨预测结果AUC值受节点向量维度影响的规律。通过观察图5中的曲线发现，较为稀疏的网络如NS、Grid和INT网络，随着节点向量维度的增加，预测结果AUC整体呈上升趋势。相反在密度较大的网络中，随着节点向量维度的增加，AUC值逐步下降。在较为稀疏的网络中，节点间分布较为松散，需要用更长的节点向量去描述网络的特征；相反在密度大的网络中，较小维度的节点向量就能够很好地描述网络特征信息，增大节点向量的维度相反弱化了重要特征信息的表征。

图5 节点向量维度与AUC

4 结 语

本文提出基于概率的随机游走来进行网络节点序列化，并将游走得到的节点序列集作为语言模型的语料库，将网络中的节点作为词典，使用SkipGram模型训练得到节点对应的节点向量。最后使用节点向量来间接计算网络中节点间的相似度，进而进行链路预测，并取得了良好的实验效果。

当然，本文提出的模型也存在一定的不足之处，虽然使用了改进的随机游走来获取更加真实反映网络特征的节点序列集，然而在利用节点序列结合SkipGram训练节点向量时并未考虑不同阶邻居的不同作用，因而一定程度上削弱了节点近邻的作用。

后续的研究着眼于思考将模型推广到有向图或者带权图中，研究跨不同网络的统一适用的模型。

[1] Lei C,Ruan J.A novel link prediction algorithm for reconstructing protein-protein interaction networks by topological similarity[J].Bioinformatics,2013,29(3):355-364.

[2] Yu Q,Long C,Lv Y,et al.Predicting co-author relationship in medical co-authorship networks[J].Plos One,2014,9(7):101-214.

[3] Liben-Nowell D,Kleinberg J.The link prediction problem for social networks[J].Journal of the Association for Information Science and Technology,2007,58(7):1019-1031.

[4] Zhu J,Hong J,Hughes J G.Using Markov Chains for Link Prediction in Adaptive Web Sites[C]//International Conference on Computing in An Imperfect World.Springer-Verlag,2002:60-73.

[5] Saruukkai B R.Link prediction and path analysis using markov chains[J].Computer Networks,2010,33(1-6):377-386.

[6] Adamic L A,Adar E.Friends and neighbors on the Web[J].Social Networks,2003,25(3):211-230.

[7] Zhou T,Lü L,Zhang Y C.Predicting missing links via local information[J].The European Physical Journal B,2009,71(4):623-630.

[8] Bengio Y,Vincent P,Janvin C.A neural probabilistic language model[J].Journal of Machine Learning Research,2003,3(6):1137-1155.

[9] Mikolov T,Chen K,Corrado G,et al.Efficient Estimation of Word Representations in Vector Space[J].Computer Science,2013,4:124-132.

[10] Shavlik J W.Proceedings of the Fifteenth International Conference on Machine Learning[C]//Fifteenth International Conference on Machine Learning.Morgan Kaufmann Publishers Inc,1998:498-517.

[12] Jaccard P.Lois de distribution florale dans la zone alpine[J].Bulletin De La Societe Vaudoise Des Sciences Naturelles,1902,38(144):69-130.

[13] Barabási A-L,Albert R.Emergence of Scaling in Random Networks[J].Science,1999,286( 5439):509-512.

[14] Cano L,Diaz R.Indirect Influences on Directed Manifolds[J].Mathematics,2015,32(5):10-26.

[15] Wang Jing,Rong Lili.Similarity index based on the information of neighbor nodes for link prediction of complex network[J].Modern Physics Letters B,2013,27(27):793-799.

[16] Bartusiak R,Kajdanowicz T,Wierzbicki A,et al.Cooperation Prediction in GitHub Developers Network with Restricted Boltzmann Machine[M].Intelligent Information and Database Systems,2016.

[17] Paparo G D,Müller M,Comellas F,et al.Quantum Google Algorithm:Construction and Application to Complex Networks[J].Eur.phys.j.plus,2014,129(7):1137-1143.

[18] Jeh G,Widom J.Mining the space of graph properties[C]//Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.ACM,2004:187-196.

[19] Blondel V,Gajardo A,Heymans M,et al.A measure of similarity between graph vertices[J].Siam Review,2004,46(4):647-666.

[20] Leicht E A,Holme P,Newman M E.Vertex similarity in networks[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2006,73(2):65-93.

[21] Clauset A,Moore C,Newman M E.Hierarchical structure and the prediction of missing links in networks[J].Nature,2008,453(7191):98-101.

[22] Kölzsch A,Blasius B.Indications of marine bioinvasion from network theory[J].The European Physical Journal B,2011,84(4):601-612.

[23] Cimini G,Medo M,Zhou T,et al.Heterogeneity,quality,and reputation in an adaptive recommendation model[J].The European Physical Journal B,2011,80(2):201-208.

[24] Zhang D,Wu C,Xiong W,et al.Study on topology design for large scale service overlay networks[C]//International Conference on Wireless Communications,NETWORKING and Mobile Computing.IEEE Press,2009:3821-3824.

[25] Pan X,Deng G,Liu J G.Weighted bipartite network and personalized recommendation[J].Physics Procedia,2010,3(5):1867-1876.

[26] Lee S G,Lee J Y,Chmielewski J.Information filtering via weighted heat conduction algorithm[J].Physica A Statistical Mechanics & Its Applications,2011,390(12):2414-2420.

[27] Getoor L.Link mining:a new data mining challenge[J].Acm SIGKDD Explorations Newsletter,2003,5(1):84-89.

[28] 李志宇,梁循,周小平.一种大规模网络中基于节点结构特征映射的链接预测方法[J].计算机学报,2016,24(5):149-157.

[29] Liang Z,Xu M,Teng M,et al.Coevolution is a short-distance force at the protein interaction level and correlates with the modular organization of protein networks[J].Febs Letters,2010,584(19):4237-4240.

[30] Newman M E.Finding community structure in networks using the eigenvectors of matrices[J].Physical Review E Statistical Nonlinear & Soft Matter Physics,2006,74(3):92-100.

[31] Watts D J,Strogatz S H.Collective dynamics of ‘small-world’ networks[J].Nature,1998,393(6684):440-442.

[32] Ackland R,Ackland R.Mapping the U.S. Political Blogosphere:Are Conservative Bloggers More Prominent[C]//BlogTalk Downunder 2005 Conference.Berlin:Springer,2005:1-12.

[33] Mahajan R,Spring N,Wetherall D,et al.User-level Internet Path Diagnosis[J].Acm Sigops Operating Systems Review,2003,37(5):106-119.

[34] Surhone L M,Tennoe M T,Henssonow S F,et al.USAir Flight 427[M].Betascript Publishing,2010:165-178.

[35] Hanley J A,Mcneil B J.The meaning and use of the area under a receiver operating characteristic (ROC) curve[J].Radiology,1982,143(1):29-36.

[36] Herlocker J L,Konstann J A,Terveen K,et al.Evaluating collaborative filtering recommender systems[J].ACM Transactions on Information Systems,2004,22(1):5-53.

ALINKPREDICTIONMETHODBASEDONSKIPGRAMMODEL

Zhao Chao1Zhu Fuxi1,2Liu Shichao1

1(SchoolofComputerScience,WuhanUniversity,Wuhan430072,Hubei,China)2(SchoolofComputerScienceandTechnology,HankouUniversity,Wuhan430212,Hubei,China)

The existing link prediction algorithm based on node similarity can hardly keep low complexity of the computation when aiming to promote prediction accuracy. Inspired by the application of probabilistic graphical model of natural language, this paper proposes a link prediction method based on SkipGram model. First, the random walk based on probability method was proposed, and the sampling sequence of the network nodes was obtained by this method. Then, the network nodes were mapped to a low dimensional vector space to reduce the complexity by combining the SkipGram model. In the end, the distance between vectors was used as the index to measure the similarity between the nodes of the network to accomplish link prediction. Through experiments and comparison in six representative real networks, the model proposed in this paper can improve the accuracy of prediction a lot.

Link prediction Vector representation SkipGram model Node similarity

TP391

A

10.3969/j.issn.1000-386x.2017.10.043

2016-11-30。国家自然科学基金项目(61272277)。赵超，硕士，主研领域：社会网络。朱福喜，教授。刘世超，博士。