利率期限结构影响因素分析
(陕西国际商贸学院,陕西 咸阳 712000)
利率期限结构影响因素分析
王飞婷
(陕西国际商贸学院,陕西 咸阳 712000)
本文利用Nelson-Siegel模型对上交所国债现券的利率期限结构进行了估计,在此基础上通过主成分分析对利率期限结构的影响因素进行提取,分析归纳利率期限结构的变动特征。通过对2008年1月至2015年12月上交所国债月度交易数据的实证研究发现,Nelson-Siegel模型中的参数因子能很好地反映利率的变动,由此可通过对参数因子的时序预测进一步预测未来时间点上的利率期限结构,从而为债券投资组合进行套期保值和货币政策制定提供参考依据。
利率期限结构;Nelson-Siegel模型;主成分分析
1.引言
利率期限结构是某一时点上,到期期限与即期利率之间的对应关系。随着研究时点的不同,利率曲线的变动趋势也不相同。准确把握利率期限结构的市场化特征,不仅可以为金融产品的定价提供基础,而且通过对利率期限结构变动趋势的研究,可进一步判断宏观经济走势,进而提供央行对未来经济的预测能力。本文用Nelson-Siegel模型对我国上交所国债1的利率期限结构进行估计,计算标准年限的利率期限结构,并在此基础上利用主成分分析以及相关分析法对影响我国利率期限结构的变动因素进行提取和归纳。
2.文献回顾
利率期限结构主成分分析是在Nelson-Siegel模型的基础上进行的,而现有文献对于Nelson-Siegel模型与主成分分析方法的结合研究较少,因此,文章主要从利率期限结构的静态估计和利率期限结构的主成分分析两方面进行文献回顾。
目前对于利率期限结构的估计主要包括静态模型和动态模型。无论采用的是静态估计还是动态估计,选择的唯一标准在于所用模型能较准确的反映特定时间点的利率变动情况。Christensen(2009)认为Nelson-Siegel模型是建立在统计思想和数学意义的基础上,但添加了无套利条件后得出的扩展模型和传统均衡模型中即期利率的表达式基本相同,进一步说明Nelson-Siegel模型具有较强的经济学含义。Diebold和Li(2006)将静态模型动态化,是以Nelson-Siegel模型为基础,建立“水平”、“斜率”和曲率等状态因子的动态化过程,同时Diebold和Li(2009)在在此模型的基础上又加入宏观经济变量,按照空间状态理论来研究上交所债券市场的利率期限结构和宏观经济变量之间的相互作用。
3.模型及方法介绍
本文用Nelson-Siegel模型对我国上交所2008年1月到2015年12月国债现券的月度交易数据,选取每月的最后一个交易日为月度交易数据。关于数据的选取一方面考虑到作主成分分析的样本数量考虑,另一方面是月度最后一天的交易数据可以从整体上反映外部环境对于利率的影响状况。
3.1 Nelson-Siegel模型介绍
在Milton Friedman(1977)指出了收益率曲线节约模型的重要意义之后,Nelson 和Siegel(1987)提出了一个简约模型,即用较少的几个参数可以拟合出不同的形状;同时在文章中,他们还利用美国短期国库券的历史数据证明了该模型完全符合Milton Friedman所指出的简约模型应达到的目标。
Nelson-Siegel模型是假定瞬时远期利率服从某一随机微分方程,具体形式如下:

其中,f(0,θ)表示在未来时间θ时发生的瞬时远期利率。β0、β1、β2、τ1均为待估参数。根据连续复利公式:

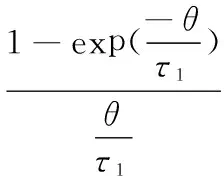
根据Diebold 和Li(2006)扩展了上述Nelson-Siegel模型,由于τ1被看成了时间常数,将τ1固定使之不随时间θ的变化而变化,这样虽然损失了一部分拟合优度,但却保证了其他参数的稳定性。其中β0,β1,β2被看作“状态因子”,其β0代表长期利率(水平因子),它表示瞬时远期利率曲线f(0,θ)渐近线,随着到期期限θ的增大,f(0,θ)曲线趋向于β0。β1代表短期利率部分(斜率因子),它是瞬时远期利率向渐近线趋近速度的衡量因素。若β1小于零,瞬时远期利率曲线随着期限的增加而上升,反之,若β1大于零,瞬时远期利率曲线随期限的增加而下降。β2代表中期利率部分(曲率因子),它决定了瞬时远期利率的性质和曲度。当β0固定,根据此模型,β1,β2的不同组合,便可得到四种不同形状的收益率曲线,包括递增、递减、水平和倒置。
3.2 基于Nelson-Siegel模型的主成分分析
本文之所以选择Nelson-Siegel模型来估计利率期限结构,是由于此模型中的待估参数具有明确的经济含义,且能较好拟合利率的变动趋势。而文中主成分分析是通过Nelson-Siegel模型验证模型中三参数(固定)取值对影响利率变动因素的解释性,在此基础上可通过对β0,β1,β2的预测来实现对未来某一时间点上利率期限结构的预测。
当τ1固定,Nelson-Siegel模型的因子载荷与期限t的关系图像如图3-1:
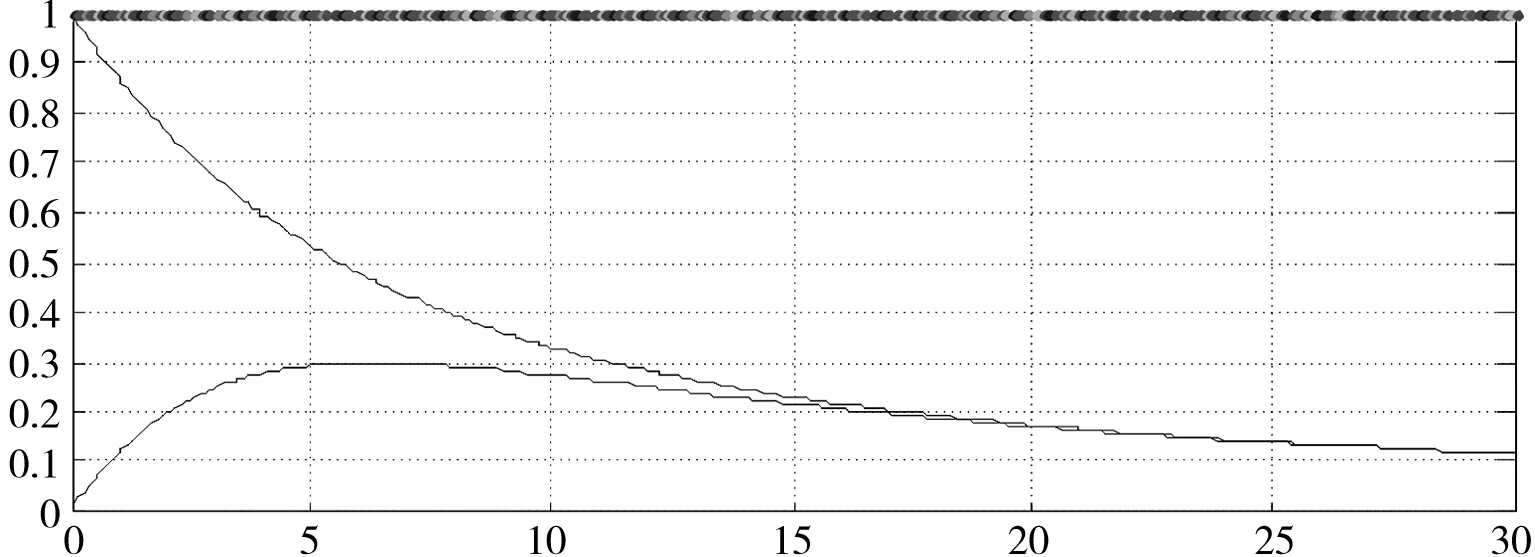
图3-1 Nelson-Siegel模型因子载荷与到期期限t的关系
总之,无论将状态因子的经济含义定义为长期利率、短期利率、中期利率或是水平因子、斜率因子、曲率因子,其本质是为了说明其对收益率曲线的决定作用。而主成分分析方法的实质是将原来具有一定相关性的众多指标,重新组合成少数几个无关的综合指标的过程。
4.实证分析
本文数据选取上海证券交易所国债现券在2008年1月-2015年12月的每月最后一天的交易数据,共96个样本数据。
4.1 Nelson-Siegel模型的实证结果检验
文章利用Nelson-Siegel模型估计利率期限结构时分为两个部分:(1)利用非线性拟合方法估计模型中的四个参数β0,β1,β2,τ1;(2)固定τ1,利用线性拟合估计出三参数β0,β1,β2。
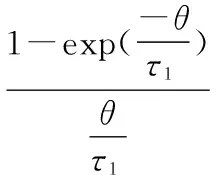
同时,根据模型的拟合参数计算每个交易日的收益率均方根误差(RMSE)和收益率的平均绝对误差(MAE)来判别模型拟合效果,其误差均保持在10个基点之内,拟合效果较好。
4.2 Nelson-Siegel模型三参数与主成分公因子的相关性检验
为了验证τ1固定,三参数β0,β1,β2确实可代表利率曲线的变动趋势,文章进一步利用主成分分析来加以验证。利用非线性拟合出Nelson-Siegel模型的四个参数β0,β1,β2,τ1,将到期期限分为0.25,0.5,0.75,1,2,3,5,7,10,15,20,30,40,50等标准年限,可以估计出这些标准年限在此8年期间的即期利率,进而对其进行主成分分析。
通过主成分分析发现提取出来的三个公因子对利率变动的累计贡献率达99%,则说明用此三个公因子足以解释利率的变动。而根据Nelson-Siegel模型可知,当τ1固定,利率的变动取决于β0,β1,β2,三参数与所提三公因子之间的相关系数为0.888,0.93,0.826。
同时,Nelson-Siegel模型(固定τ1时)三参数与主成分所提三个公因子之间的趋势图如图4.1、4.2、4.3、4.4、4.5、4.6:

图4.1 图4.2
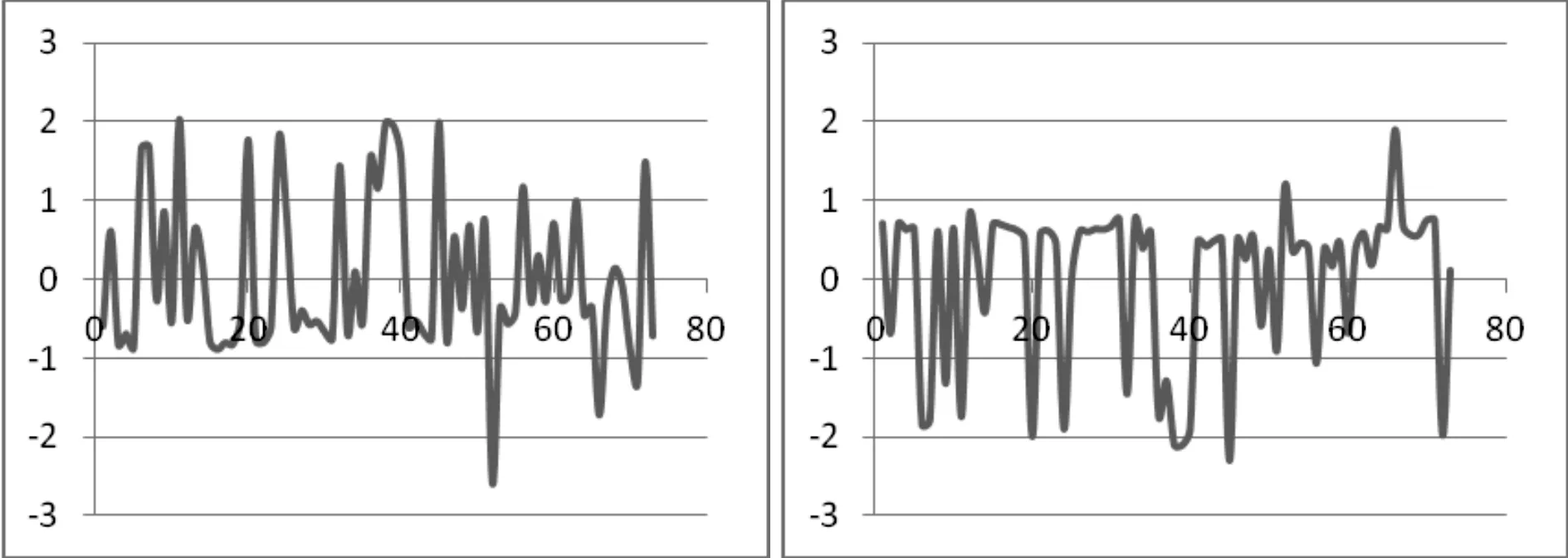
图4.3 图4.4
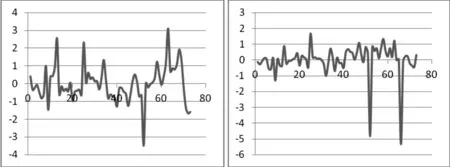
图4.5 图4.6
上述结果进一步表明,模型中的三个待估参数β0,β1,β2的取值可以较充分解释利率的变动情况。
5.结论
本文利用Nelson-Sigel模型估计了上交所过去8年国债交易的利率期限结构,通过对其中样本进行抽样检验发现,Nelson-Siegel模型能较好反映利率的变动趋势,在此基础上结合主成分分析表明,NS模型中待估参数与主成分所提公因子之间存在高度相关关系,进一步验证模型参数对于利率变动的具有较强解释性。基于本文研究结果,不但可以为债券定价提供依据,还可为央行制定货币政策提供参考。
同时,本文通过实证分析解决了Nelson-Siegel模型在参数固定时,剩余三个代表水平、斜率以及曲率的参数对于利率的变动趋势具有重要影响,在此基础上,便可通过对模型三参数的预测来进行后续研究,来预测未来某一天的利率期限结构,进而为新债券的发行以及债券投资组合进行套期保值提供参考。
[1] 朱峰.零息国债收益率曲线变化特征的因素分析[R].第二届中国青年经济学者论坛,武汉,2002.
[2] 林海.基于套期保值的主成分分析[R].厦门:厦门大学,2004.
[3] 许瑾,缪柏其.利率期限结构的主成分分析[J].数理统计与管理,2004,23(2):20-22.
[4] 刘海东.利率期限结构的静态分析和动态特征[J].山西财经大学学报,2006,5:99-102.
[5] 于鑫.宏观经济对利率期限结构的动态因素影响研究[J].南方经济,2009,6:25-31.
[6] 夏日.中美两国利率期限结构的主成分分析[J].对外贸易,2014,1:47-48.
[8] 余文龙,王兴安.基于动态Nelson-Siegel模型的国债管理策略分析[J].经济学季刊,2010,4:1403-1426.
[9] 朱世武,陈健恒.利率期限结构理论实证检验与期限风险溢价研究[J].金融研究,2004,5:78-88.
[10] 王飞婷.基于Nelson-Siegel模型的银行间债券市场利率期限结构研究[R].兰州理工大学,2015:3-5.

