随机中断和随机需求下闭环供应链最优回收定价模型

权蓉　颜荣芳

摘要讨论了由一个制造商、一个零售商和一个第三方回收商组成的闭环供应链的差别定价问题.基于博弈论的理论和方法在集中式和分散式决策情形下分别建立了第三方回收定价模型，并给出了随机中断和随机需求下闭环供应链的最优定价策略组合，最后通过数值例子分析了供应中断对最优批发价和零售价的影响.

关键词物流与供应链管理；随机中断；博弈论；差别定价

中图分类号F270.7文献标识码A

Optimal Collection Pricing Model for ClosedLoop Supply Chain under Stochastic Disruption and Stochastic Demand

Rong QUAN，Rongfang YAN

（College of Mathematics and Statistics，Northwest Normal University，Lanzhou，730070，China）

AbstractThis paper discussed the problem of the differential pricing of closedloop supply chain consist of one manufacturer，one retailer and a third party recycler.Based on the theory and method of game theory，we established the third party collection pricing model under the situation of centralized and decentralized decisionmaking，and provided the optimal pricing strategy combination of closedloop supply chain under stochastic disruption and stochastic demand.Finally，the numerical example illustrated how the supply disruption affected the optimal wholesale price and retail price.

Key wordslogistics and supply chain management；stochastic disruption；game theory；differential pricing

1引言

全球经济的快速发展导致自然资源的严重短缺，为了经济社会的可持续发展，研究如何对废旧品回收再利用已经成了近几年来国内外普遍关注的问题.为了应对废旧品的回收再利用，各个国家制定了许多相应的法律法规.例如，美国在1984年颁布了《资源保护和回收法》（简称RCRA）；日本在1991年实施了《资源有效利用促进法》；中国在1998年生效的《废家用电器再利用法》等等.为了响应国家号召，且废旧品再加工的成本通常情况下都比较低，所以大多數企业都参与了供应链的再制造过程，如施乐公司、惠普公司.因此对于闭环供应链的研究变得刻不容缓.

闭环供应链管理的目的是为了促进社会经济与环境的综合绩效，从而使经济和环境达到双赢.所谓的闭环供应链是在传统生产消费模式下增加了废旧品回收再利用环节.目前国内外学者关于闭环供应链的研究主要集中在随机需求、差别定价和协调问题等领域.Jianmai Shi等（2010）[1]研究了闭环供应链系统的最优生产和定价策略问题，其中假定新产品和再造品无差别定价，没有考虑产品在差别定价下的随机需求与回收对价格的影响.Geraldo Ferrer等（2010）[2]讨论了具有差别定价的新产品和再造品的多周期生产和定价问题.JenMing Chen，ChiaI Chang（2012）[3]在合作和竞争情形下分析了再制造闭环供应链的策略问题，分析结果表明策略决策取决于两种情形下再制造成本和竞争强度.Jie Wei，Jing Zhao（2013）[4]研究了闭环供应链不同渠道下不同选择的问题，应用博弈论和模糊论获得了公司的最优策略.Min Huang等（2013）[5]建立了零售商和第三方同时竞争回收旧产品的闭环供应链最优决策博弈模型，得到最优价格和回收策略，证明了回收渠道的最优决策与制造商和零售商的回收竞争强度有关.付小勇等（2014）[6]运用博弈理论方法建立了市场机制下处理商回收渠道选择博弈模型，并用数值仿真分析了博弈均衡结果.Xiang Li等（2015）[7]研究了在随机需求和随机产量下的再制造闭环供应链的定价决策问题，发现了先再制造后定价策略有较低的再制造成本、较高的缺货罚金和挽救价值.T.Maiti，B.C.Giri（2016）[8]在零售价格和产品质量依赖于需求的情况下，探究了具有第三方回收的闭环供应链决策问题，但其中新产品和再造品具有相同的价格和需求.B.C.Giri ，S.Sharma（2016）[9]考虑了在供应中断下具有不确定需求和回收的闭环供应链系统，通过一些特殊分布得到供应链最优生产策略.大多数文献的研究都是假定新产品和再造品在市场上销售完全没有区别，即按照相同的市场价格和需求出售.现实中，虽然能够实现再造品质量、性能与新产品相同，但是消费者往往对两种产品是加以区分的.

不同于以上文献，这里主要研究了由制造商、零售商和第三方组成的第三方回收模型的闭环供应链系统.在新产品和再造品存在价格差异且两者之间不是独立的，各自的市场价格都会影响对方需求的情形下，讨论了具有随机中断和随机需求的闭环供应链最优定价策略问题.并在数值算例中分析了最优批发价、销售价与中断的关系.endprint

2模型假设及符号说明

考虑由一个制造商、一个零售商和一个第三方所组成的闭环供应链中第三方回收问题.制造商利用原材料和废旧品生产新产品和再造品，制造商可以从两个供应商处获得原材料，其中主要供应商非完全可靠（供应可能中断），次要供应商完全可靠，当然主要供应商的价格要低于次要供应商的价格.由于消费者对新产品和再造品的认知不同，因此制造商以不同的批发价批发给零售商，零售商再以不同的零售价卖给消费者.当这些产品寿命终结成为废旧品时，第三方以一定的回收补贴价从消费者处回收，最后由制造商利用废旧品进行再制造，将再造品与新产品以不同的价格进行销售，形成一个完整的闭环供应链.

设新产品的单位生产成本、批发价和零售价分别为cm、w3和p1，再制造品的单位生产成本、批发价和零售价分别为cr、w4和p2.第三方从消费者处回收废旧品，在交易过程中回收品的单位服务费用为At.制造商从回收品中获得的单位利润为ct.令=Fτ表示制造商与第三方的合同费用，它是回收率τ的函数，其中F是制造商的决策变量.主要和次要供应商的单位原材料批发价格为w1和w2，主要供应商发生供应中断的概率是p，零售商对新产品和再造品的订购量分别为Q1和Q2.新产品和再造品的库存因子分别为z1和z2，且是外生变量.为了便于问题的讨论，进一步假设：

（1）主要供应商的单位批发价格低于次要供应商的，即w1

（2）再造品的单位生产成本、批发价和零售价低于新产品的单位生产成本、批发价和零售价，即cr

（3）废旧品的回收率为τ（0<τ<1），即回收的废旧品可全部用于再制造.回收废旧品的固定投入成本是废旧品回收率τ的函数，固定投入成本表示为Bτ2（B>0）；

（4）零售商对新产品和再造品的单位缺货成本分别为s1，s2，单位产品的挽救价值分别为h1，h2；

（5）对消费者而言，新产品与再造品互为完全替代品，新产品对再造品的价格具有需求弹性，再造品对新产品的价格也具有需求弹性.

基于以上假设，闭环供应链新产品和再造品的市场需求可以表示为

其中δ是产品的市场容量，θ（0<θ<1）为新产品需求的市场份额，α1和α2分别是新产品和再造品需求的价格敏感系数，β1和β2分别是新产品和再造品的交叉价格敏感系数.假设产品零售价对自身的影响大于交叉价格的影响，即0<βi

3分散式条件下闭环供应链回收定价模型

所谓分散式决策，是指制造商、零售商和第三方分别以各自的利润最大化为决策目标，确定新产品和再造品的批发价、零售价、回收率及合同变量的决策模式.在分散式条件下，假设制造商与零售商的关系为Stackelberg博弈关系，且制造商为领导者，零售商为跟随者，制造商决定决策变量F和新产品、再造品的批发价w3、w4，零售商根据制造商决定的批发价来决定新产品和再造品的零售价p1，p2，由第三方决定产品的回收率τ，各自都以其利润最大化为决策目标进行定价.因此可以将分散式决策下闭环供应链的决策问题归结如下：

分散式决策下闭环供应链的最优差别定价问题可以表示为如下的Stackelberg博弈模型.

下面的命题1和2给出了分散式条件下新产品和再造品的最优零售价和批发价，以及废旧品的最优回收率和制造商的合同变量.

命题1在分散式决策条件下，把库存因子z1，z2视为外生变量，对于固定的z1，z2，存在使零售商和第三方利润最大的最优零售价格组合（p*1，p*2）和最优回收率ψ*.

证明容易验证E[πr]关于p1，p2是严格联合凹的，E[πr]关于τ是严格凹的，所以E[πr]关于p1，p2有最大值，E[πt]关于τ有最大值.由利润最大化的一阶条件可得到最优零售价p*1，p*2和最优回收率τ*分别为

显然由E[πr]是关于p1，p2的凹函数，E[πt]是关于τ的凹函数，所以在满足一阶条件的情况下，零售商和第三方公司都获得了最大的利润.

注1存在足够大的正常数B，当回收率0<τ<1时，有

B>ctAtG（α1+α2-β）（α1α2-β1β2）.

命题2在分散式决策下，对于固定的z1，z2，存在使制造商利润最大的最优批发价格组合（w*3，w*4），以及制造商的合同变量F*.

证明由注1可知，E[πm]关于w3，w4和F的Hessian矩阵的一阶主子式对应行列式的值

二阶主子式对应行列式的值

三阶主子式对应行列式的值

因此E[πm]关于w3，w4和F是严格联合凹的，所以在满足一阶条件的情况下制造商获得最大的利润.

由于E[πm]关于wM3，w4和F是严格联合凹的，所以E[πm]关于w3，w4和F有最大值，由利润最大化的一阶条件立即得到最优批发价格w*3，w*4和合同变量F*分别为

4集中式条件下闭环供应链回收定价模型

所谓集中式决策，是指为了使整个闭环供应链利润最大化，制造商、零售商和第三方通过协商共同决定批发价、零售價以及回收率的决策模式.因此，由式（1）、式（2）和式（3）得到集中式决策下闭环供应链的总利润：

集中式系统的决策问题可归为如下的最优化模型：

下面的命题3给出了集中式条件下新产品和再造品的最优零售价和最优回收率.

命题3在集中式决策下，存在使系统利润最大的最优零售价格组合（p**1，p**2）和最优回收率τ**.

命题3的证明类似于命题1和命题2的证明，这里不再赘述.

5數值算例

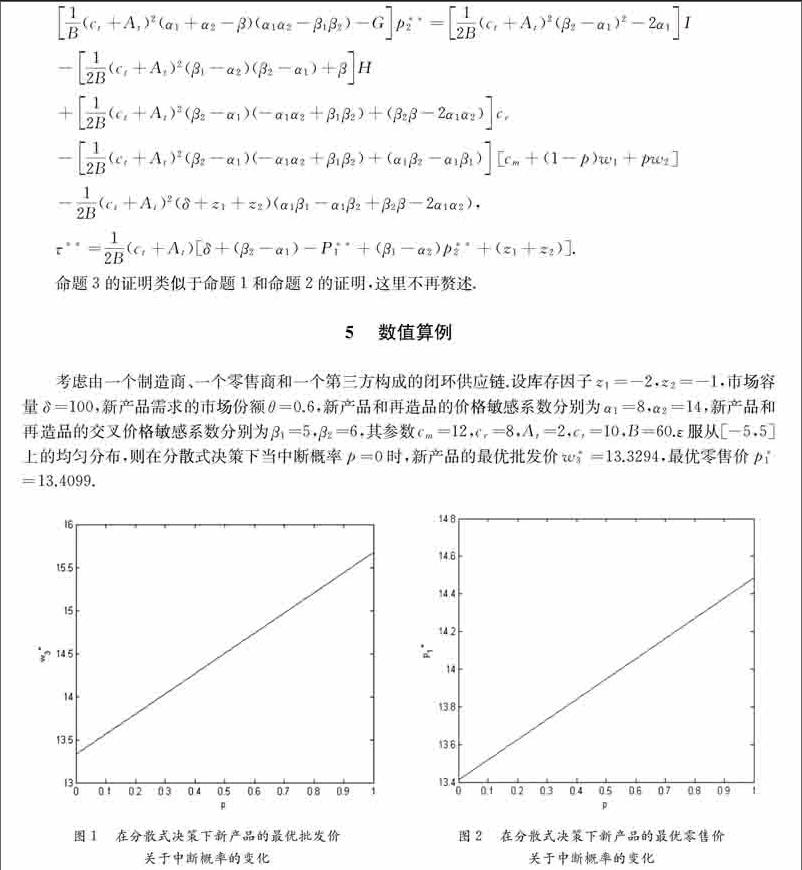
考虑由一个制造商、一个零售商和一个第三方构成的闭环供应链.设库存因子z1=-2，z2=-1，市场容量δ=100，新产品需求的市场份额θ=0.6，新产品和再造品的价格敏感系数分别为α1=8，α2=14，新产品和再造品的交叉价格敏感系数分别为β1=5，β2=6，其参数cm=12，cr=8，At=2，ct=10，B=60.ε服从[-5，5]上的均匀分布，则在分散式决策下当中断概率p=0时，新产品的最优批发价w*3=13.3294，最优零售价p*1=13.4099.

在以上参数假设下，中断概率对最优的批发价和零售价会产生一定的影响.在分散式决策下，新产品的最优批发价和零售价关于中断概率求导，得到最优批发价和零售价关于中断概率是正相关的.对于给定的中断概率p，得到最优批发价w*3和零售价p*1关于中断概率的表达式，具体情况如图1、图2.图1给出了在分散式决策下新产品最优批发价随着中断概率的变化情况.图2给出了在分散式决策下新产品最优零售价随着中断概率的变化情况.

由图1、图2可以得到下面的注2.

注2在分散式决策下，新产品的最优批发价和最优零售价随着中断概率的增大而增加.因此，主要供应商发生中断时，最优批发价格增加，零售商就会选择完全可靠的次要供应商.相应的再造品的最优批发价和最优零售价与中断概率的关系类似.

6结束语

研究了分散式和集中式情形下的第三方回收的再制造闭环供应链的最优差别定价模型，得到了新产品和再造品的最优定价策略组合和最优回收率及制造商的合同变量，并进一步分析了最优定价与中断概率的关系.结果表明：新产品和再造品的最优批发价和最优零售价会随着中断概率的增大而增加.因此，在实际供应链运作中，若主要供应商发生中断则最优批发价格增加，零售商就会选择完全可靠的次要供应商来完成供应链的运作.本文只研究了制造商、零售商与第三方的闭环供应链系统，在实际生活中的真实情况远比此复杂，因此还有待于我们深入研究.

参考文献

[1]Jianmai Shi，Guoqing Zhang，Jichang Sha.Optimal production and pricing policy for a closed loop system[J].Resources，Conservation and Recycling，2010，55（6）：639-647.

[2]Geraldo Ferrer，Jayashankar M，Swaminathan.Managing new and differentiated remanufactured products[J].European Journal of Operational Research，2010，203（2）：370-379.

[3]JenMing Chen，ChiaI Chang.The coopetitive strategy of a closedloop supply chain with remanufacturing[J].Transportation Research，2012，48（2）：387-400.

[4]Jie Wei，Jing Zhao.Reverse channel decisions for a fuzzy closedloop supply chain[J].Applied Mathematical Modelling，2013，37（3）：1502-1513.

[5]Min Huang，Min Song，Loo Hay Lee，Wai Ki Ching.Analysis for strategy of closedloop supply chain with dual recycling channel[J].Internatioal Journal of Production Economics，2013，144（2）：510-520.

[6]付小勇，朱庆华，赵铁林.基于逆向供应链间回收价格竞争的回收渠道选择策略[J].中国管理科学，2014，22（10）：72-79.

[7]Xiang Li，Yongjian Li，Xiaoqiang Cai.Remanufacturing and pricing decisions with random yield and random demand[J].Computers Operations Research，2015，54：195-203.

[8]T.Maiti，B.C.Giri.A closed loop supply chain under retail price and product quality dependent demand[J].Journal of Manufacturing Systems，2015，37：624-637.

[9]B.C.Giri，S.Sharma.Optimal production policy for a closedloop hybrid system with uncertain demand and return under supply disruption[J].Journal of Cleaner Production，2016，112：2015-2028.endprint