确定越流含水层参数的混沌序列优化算法
张晓周+卢玉东+郭建青


摘要:将混沌序列优化算法应用在第一类越流系统含水层非稳定流井流问题上,进行抽水试验数据的分析、含水层参数的求解,并就算法的搜索能力和结果与给定含水层各参数取值范围的关系进行探讨。结果表明:(1)求解越流条件下含水层参数的计算问题能用混沌序列优化算法得到很好的解决;(2)除越流因数上限取值会降低越流因数搜索结果的准确性外,储水系数、导水系数、越流因数上限取值对算法的搜索能力和搜索结果没有太明显的影响。相较于其他方法,混沌序列优化算法易于编程、运算简单、运算结果不被人为因素干扰等特点更为突出。
关键词:混沌序列优化算法;越流系统;越流因数
中图分类号:TV139.14 文献标识码:A 文章编号:1672-1683(2017)05-0116-05
标准曲线对比法、拐点法、切线法在确定含水层参数的过程中得到了广泛的应用,但是在实际操作中,由于人为的随意性与作图时的差异性,使得不同人得出的结果不尽相同。针对于此,石志远等利用神经网络和遗传算法等不同新型方法对水文地质参数进行求解,一定程度上规避了人为因素的干扰。郭建青教授以泰斯井流为例,对比了混沌序列优化算法、泰斯配线法、Sushil简单法等不同的求解水文地质参数方法,发现混沌序列优化算法结果可靠,并且,由于混沌序列优化算法可以直接进行随机搜索,目标函数简单等特点,其具有较广的应用领域;此外混沌序列优化算法的搜索过程是通过编写程序完成的,整个过程涉及到的人为干扰因素很少,其计算结果具有客观性、稳定性、时效性,与传统的配线法相比具有很大的优势。然而,文献[6]仅对无越流条件下的单孔数据进行了分析,对于混沌序列优化算法在具有越流含水层条件下的应用并未进行研究。因此,笔者以分析第一类越流系统的单孔抽水试验资料,确定含水层参数的问题为例,进一步探究混沌序列优化算法在确定含水层参数中的应用。
1混沌序列优化算法的思路
算法的整个运行过程包括以下两个阶段。
首先确定一个能够得出遍历性轨迹的迭代方法,使得此轨迹能够对整个混沌序列进行搜索。当达到一定的限定条件后停止此阶段搜索,并认为该搜索的最优结果已接近含水层参数的最优值,并以该结果作为下一搜索阶段的搜索起点,此为粗搜索阶段。然后,以上一过程求得的参数值作为基准值,并附加一个微小的干扰进行进一步的搜索,直至完成整个搜索过程,此为细搜索阶段。通过高斯分布、均匀分布产生的随机变量,按梯度下降机制得出的混沌变量均可作为此处附加的微小扰动。
通过与载波相似的思想,将优化变量选为由Logistie映射生成的混沌变量,定义域选为混沌运动的搜索空间,进而对待求参数在混沌变量中实施搜索過程,其详细步骤如下:
3算例
3.1数据来源
采用文献[19]中一眼观测井(距主抽水井1219m,抽水流量为2936 m3/d)的抽水数据来验证混沌序列优化算法在第一类越流系统中的应用。由于文中采用的汉图什计算方法时,是将观测井363 min到850 min之间的7个相关性较好的数据放在一起计算的。所以,在进行混沌序列优化算法的时候也采用同样的数据。
3.2结果对比
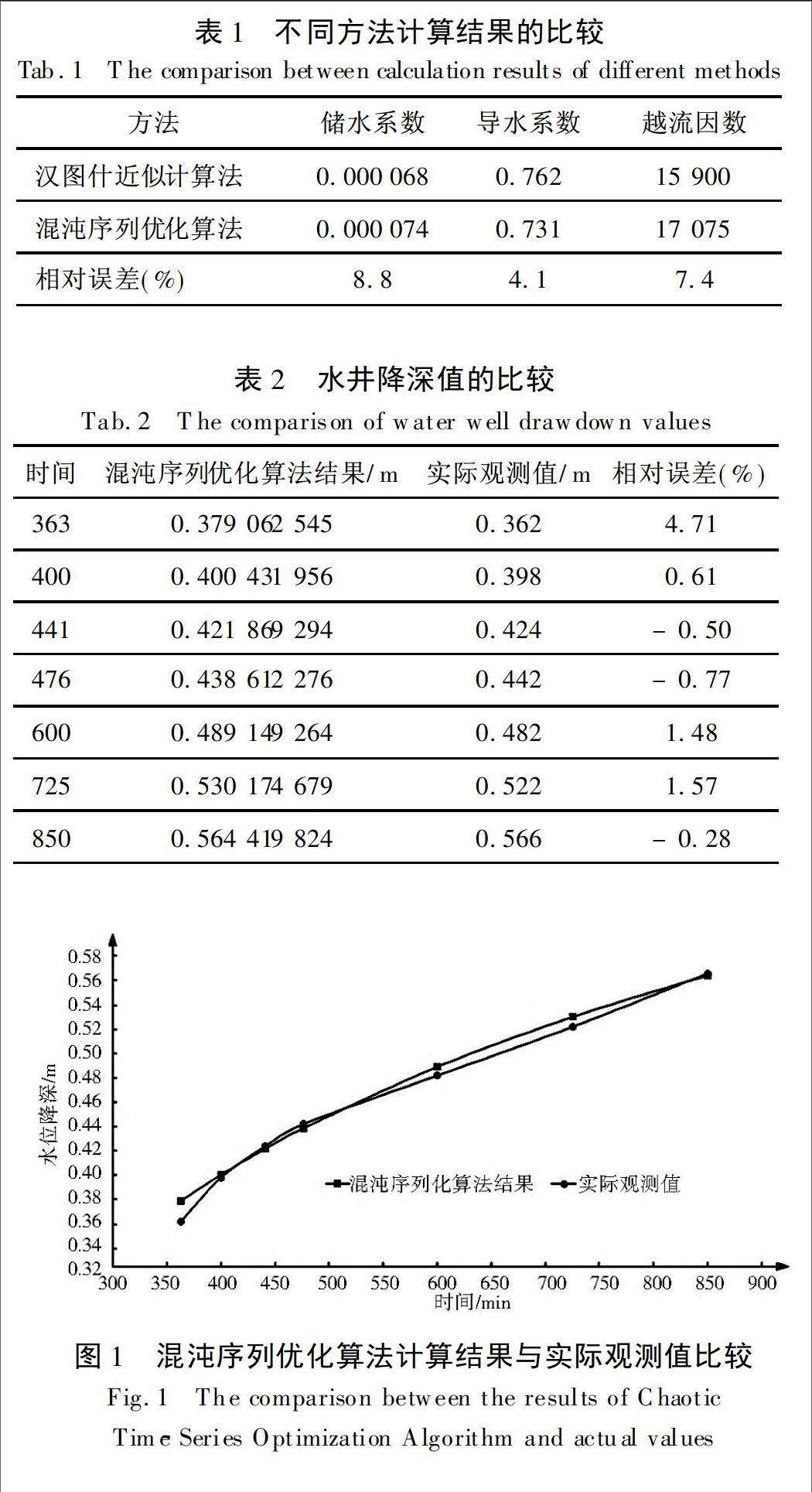
通过VB编程对含水层各个参数进行优化计算时,给出的参数初始取值和其它因子的取值分别为:导水系数为0.4~1.99,储水系数为0~0.015,越流因数为15 800~16 000,粗搜索收敛值为0.000 051,细搜索收敛值为0.000 05。当粗搜索次数为2,混沌序列长度为400时,最后的细搜索次数为4,其它搜索结果及降深的历时曲线见表1、表2及图1。
如表1中所示,用混沌序列优化算法的搜索结果与汉图什近似计算法的结果是极其接近的,参数计算结果相对汉图什近似计算结果的最大误差为8.8%,导水系数的结果尤为准确,误差仅仅为4.1%。
在表2参数结果计算准确的前提下模拟出来的水井降深结果与实际观测值相比,相对误差除初始值外,其余均在2%之内。由图1降深曲线对比图也可以看出,在抽水试验的400 min、441 min、476min与850 min,模拟值与观测值几乎重叠,说明混沌序列优化算法对水井降深的模拟结果也是非常准确的。
4算法参数的控制
4.1收敛值的影响
收敛值的大小在混沌序列优化算法中直接决定了搜索的精度与速度,在水文地质初始参数与前文不变,粗搜索次数限定在100,混沌序列长度为500,细搜索的收敛值设为0.000 043的条件下,收敛值与搜索次数的关系见表3:无论是粗搜索次数还是细搜索次数,都随着粗搜索收敛值的减小而减小,这是由于当粗搜索收敛值与细搜索收敛值相差较大时,在限定的100次搜索次数完成后,细搜索仍达不到收敛值的要求而重新进行新的搜索造成的。在实际应用中,粗收敛值与细收敛值越接近越好,以便更快的完成整个计算过程。
4.2混沌序列长度的影响
混沌序列的长度是在Logistic的迭代下实现的,状态空间的大小是由混沌序列的大小来反映的。混沌序列长度越长,可供算法搜索的空间就越大,搜索就越充分,并且越不会轻易偏离实际值。理论上说,序列长度在无穷大的时候,搜索的精度达到最高,但这样必然会加大搜索时间,况且在实际应用中这也是不现实的,为此,在本算例中,混沌序列的长度选定在50~1000之间的8组数据进行试验分析。搜索结果见表4。
从表4中可以看出,在同一粗搜索次数下,细搜索次数随着序列长度的增加有明显的减小,尤其在序列长度较小时,细搜索次数减小的最快。这是由于在粗搜索过程中,经过的序列长度越长,搜索的也越充分,得出的结果也越接近参数的真实值。但是,当长度超过600时,搜索程度已经足够充分,这种变化就不再明显。就本文实例来说,搜索长度控制在100~600之间较为适宜。
4.3粗搜索次数的控制
表4中,序列长度在50~400之间时,细搜索次数并没有随着粗搜索次数的增加而有明显的变化趋势(增加或减少),说明在此序列长度范围内,影响细搜索过程的主要因子并不是粗搜索次數。也就是在有限的序列长度内,少次数的粗搜索已使算法达到很充分的搜索程度,增加粗搜索次数不会再提高粗搜索阶段结束时的搜索精度,对于细搜索阶段的影响小于序列长度的影响。当序列长度达到500后,细搜索次数在粗搜索次数增加时呈现出减小的趋势,这是由于序列长度的增加使得少次数的粗搜索过程满足不了搜索的精度造成的。
4.4待估参数初值范围的影响
为了避免传统梯度搜索算法在求解非线性函数优化问题时,由于待估参数初值选取不当,造成搜索失败或者搜索结果不唯一的情况出现,我们在探究混沌序列优化算法中待估参数初值范围选取对搜索能力和结果的影响时,首先限定储水系数和越流因数的初始取值范围与前文一致,而将导水系数下限取为0.4保持不变,上限分别取为1.99的2~5000倍之间的12个值进行试验分析,细搜索次数与导水系数计算结果分别见表5、表6。
从表5中可以看出,无论是在相同搜索次数不同序列长度的情况下,还是相同序列长度不同搜索次数的情况下,随着导水系数初值的增加细搜索次数虽有波动,但都有逐渐增大的趋势。值得注意的是,由表6中的数据显示,混沌序列优化算法的搜索过程均未出现不收敛的情况,导水系数的搜索结果均在0.693~0.744之间,与汉图什计算的结果十分接近。说明参数初值的选取虽会影响算法的搜索速度,但对其搜索能力与搜索结果没太明显的影响。
储水系数和越流因数采用相同的处理方法后,也有同样的结果,只是越流因数的搜索结果的波动会随着初值的增大而增大,从而降低了搜索结果的准确性。
5结论
通过以上算法步骤的介绍以及实际案例的验证分析,能够得出以下结论:(1)函数粗搜索收敛值和细搜索收敛值要足够小并且越接近越好;(2)选定混沌序列长度在100~600之间、粗搜索次数在2~20之间对本案例较为适合;(3)算法的收敛性不受待估含水层参数初值范围的影响,鉴于越流因数对搜索结果的影响,含水层各参数初值范围应尽量与待估参数参考值接近。所以,对于分析第一类越流系统含水层抽水试验、确定含水层参数的问题,混沌序列优化算法是一种新的选择。

