地震作用下呷爬滑坡的变形特征分析

马斌　李昕尧　梁超

摘要：运用有限差分软件FLAC，建立了呷爬滑坡体三维模型，分别施加1倍和3倍El-Centro地震波。计算结果表明，1倍地震波作用下会发生一定的永久位移，但不会滑动失稳；3倍地震波作用下将发生滑动失稳。进一步发现边坡在1倍和3倍地震波激励下的变形滑移特征不同，第一种情况属于累积效应阶段，变形主要集中于滑体O，第二种情况属于触发效应阶段，滑体N的滑动变形同样剧烈。文中从滑坡体的组成物质和材料参数、滑动区域的地形因素和滑动区域的动力响应三方面进行了分析。运用Newmark有限滑动位移法，基于滑体N和滑体O的加速度响应时程，计算了两者的永久位移，结果与数值计算吻合良好。表明滑体O处的动力响应会产生更大的永久位移，从而验证了数值计算的结果。同时，基于结构动力响应而计算得到的永久位移也可以作为衡量地震作用对该处结构变形影响的指标，从而估计地震对局部结构的破坏作用。

关键词：呷爬滑坡；变形特征；Newmark 方法；永久位移；加速度响应

中图分类号：TU443 文献标识码：A 文章编号：1672-1683（2017）05-0110-06

对于人口分布稀疏的山区，地震触发的滑坡、山体崩塌以及泥石流等灾害所造成的损失往往比地震造成的直接损失更大。对于20世纪末到21世纪初发生的台湾集集地震、汶川地震、雅安芦山地震，均伴随多次大规模滑坡和其它次生灾害，其人员伤亡和财产损失不亚于一场地震。因此，地表运动激励下的滑坡体稳定性分析逐渐被岩土工程界和地震工程界所重视。近年来，专家学者对于地震作用下边坡的失稳机制和动力特性进行了大量研究。何蕴龙等通过有限元对滑坡体进行了动力分析，可以近似计算滑坡所受到的地震作用；祁升文等对各种情况下滑坡的动力响應进行了数值模拟与分析，总结出了高、低边坡的动力反应形式；言志信等对于顺层岩质滑坡体地震激励下的加速度响应规律、频谱特性、破裂面发生位置以及失稳判定条件进行了研究，并对耦合地震波作用、多级平台和黄土地质等情况进行了较为全面的研究；徐光兴等结合Newmark方法，提出了根据加速度预测边坡永久位移的数学模型；张雪东等运用FLAG3D有限差分商业软件分析了锦屏库区呷爬滑坡在静力作用下的变形特征和稳定性；殷跃平等结合大量的现场资料，分析了大光包巨型滑坡的失稳机制和动力响应。本文根据呷爬滑坡体变形监测图及地形图，建立了滑坡体模型，运用FLAC对其动力作用下的变形特征进行了分析，并结合New-mark数值计算法利用边坡地震响应计算了边坡的永久位移。

1模型建立

1.1滑坡体地质概况

呷爬滑坡位于锦屏水电站库区上游右岸，距离坝址约11.5 km。雅砻江流经该滑体处的河道较顺直，流向约为N12°E。该处河谷宽阔，左岸山体较为平缓，并有河漫滩、阶地发育；右岸山体呈反向坡，岸坡的坡度约为35°。

雅砻江岸坡岩层产状在呷爬滑坡处呈N 10～30°E/SE ∠85°，岩层主要由三叠系杂谷脑组深-灰黑色粉砂质板岩夹变质细砂岩组成。

呷爬滑坡体的平面投影呈长条状，具有完整的圈谷地貌。滑体靠近雅砻江一侧高程较低，为l 655 m，与枯水期雅砻江水位相同，靠近山体一侧高程较高，为2 120m，滑体前后缘高差为465 m。滑坡体的纵长约为880m，宽度在260到300 m之间，表面面积约为Q 28 km²，滑坡残体体积约为1 300万m³。

滑坡表面可见3级平台，3级平台高程分别为1775～1840 m、1880～1925m、2010～2100 m，坡度为17～18°，原为耕地。在第一和第二级平台中发育有两条纵向冲沟。其中，一条位于滑坡轴线的北侧（1号沟），另一条位于滑坡轴线的南侧（2号沟），南侧冲沟比北侧冲沟更为深长。

在滑坡体临江侧到中部，表层岩体主要由块碎石土组成，块碎石土的成分为粉砂质板岩、泥岩和砾岩；在滑坡中部到靠近山体一侧，表层岩体主要由孤石，块碎石土，解体不完全的粉砂质板岩、变质细砂岩和砾岩等组成；滑体物质分层明显，据钻孔揭露，孔深27.97～39.57 m以上，为褐黄、灰黄色块碎石土，以下至77.08～81.80 m为破碎的岩石碎块夹黏土，局部岩体保留有原始层面。

在滑坡临江侧和两条冲沟内，可见明显的滑带出露。出露的滑带在剪出口处反翘，根据地址勘察结果，其产状为N15°E/SE∠22°。滑带的主要组成物质为灰黑色泥夹碎石并带有大量石英颗粒，其中碎石成分为炭质板岩、变质细砂岩等，滑带在滑体范围内平均厚度为1～3 m，局部可达8 m，上述滑带组成物质在干燥时刚度较大，含有一定水分后刚度显著减小。

1.2建立数值模型

模型建立是FLAC^3D的短板，本文采用先在CAD中生成面域，导入AN SYS划分网格，再利用清华大学郑文棠博士开发的ANSYS2FLAC3D程序将复杂的地质体模型数据变换为FLAC³⁰内部代码，从而实现模型导入。

为了模拟地震波在滑坡体中的传播，避免在不同介质的分界面上产生与实际情况不符的反射和折射，必须设置合理的边界条件。本文在有限元模型四周网格设置自由场边界条件，它的原理是在边界节点上添加水平和垂直阻尼器来达到边界条件与主体网格的耦合，并将自由场网格所受的不平衡力传递给主体网格。自由场边界条件对入射角大于30°的波具有良好的衰减效果。对于呷爬滑坡体的基岩，由于其变形模量较大，假定为刚性地基，因此底部可不设置自由场边界条件，直接输入地震加速度时程。边界条件见图2。

本文采用局部阻尼形式，局部阻尼通过增加或减少节点的质量，达到衰减振动的目的。阻尼比取为0.157。表1给出了滑坡体数值模型建立需要的材料。

根据文献[15-16]的研究，网格的最大尺寸应不大于最小波长的1/10到1/8，兼顾模型的计算速度，网格最大尺寸取为15 m，局部网格更小。endprint

2边坡的变形特征分析

2.1地震波输入

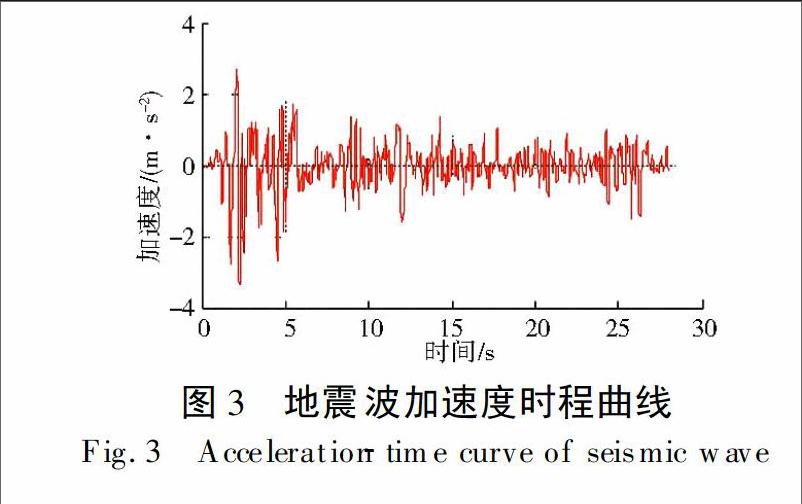
根据呷爬滑坡现场覆盖层剪切波速大约在460～490 m/s，地表覆盖层平均厚度约为90 m。根据文献[17]规定，该场地为二类场地，因此选择适用于二类场地的El-Centro南北向地震波经滤波和基线调整后，作为输入地震波，取其持续时间为28 s，峰值加速度为3.417 m/s²，加速度时程曲线见图3。

边坡在动力作用下产生的位移场直接反应了其变形特征和破坏程度。加速度场作为动力响应的最基本资料，具有重要意义。因此本文主要从位移场分析滑坡体的变形特征和稳定状态，并基于New-mark-β法和模型加速度响应计算了模型不同点处的永久位移。

2.2不同状态下的边坡变形特征

图4给出了滑坡体位移监测点布置隋况。为了分析不同情况下的滑坡体变形特征，本文分别将El-Centro加速度时程乘以1和3的系数输入，其中1倍和3倍加速度时程峰值为3.417 m/s²和10.251m/s²，分别代表一般地震作用和较极端的地震作用，从而综合分析两种情况下滑坡的变形特征和失稳破坏情况，以揭示同一滑坡体在不同峰值特性动力输入情况下的变形特征的不同。对于单个单元，如果应力等于屈服应力，将产生较大的塑性变形。但对于整个滑坡体模型，只有当滑体或滑动面上所有单元均处于塑眭变形状态且应变大于一定值时，滑动才会发生。可以预见，当地震动达到峰值时，监测点对应单元容易进入塑性状态，但当地震后期地震动趋于小幅平稳振动时，塑性单元将受到周围处于弹性变形的单元或其它边界约束条件的影响，使其变形受到限制。这时，若监测点位移仍具有变形趋势（即残余速度），则表明监测点附近单元或滑面对应单元均进入塑性变形阶段，位移持续增大，滑坡体破坏。因此，本文将监测点产生一定的永久变形，并且在地震动结束时仍然具有残余速度作为滑坡体滑动失稳的判据。图5給出了滑坡体位移云图和关键点监测位移时程，施加1倍地震波后，所有测点先急剧变形，而后在15 s左右变形停止，基本处于稳定状态，直至地震结束，不符合滑动破坏判据，因此认为滑坡体产生了一定的永久位移，但并未滑动失稳。3倍地震波输入后，滑体N和滑体O持续大幅变形，地震结束时变形呈发散状态，监测点仍具有残余速度（E点速度为0.17 m/s），符合滑动判据，因此认为滑体N和滑体O处于滑动失稳状态；小滑坡体测点变化趋势与1倍地震输入相同，因此处于稳定状态。

值得注意的是两种情况下滑坡体的变形滑移特征不同，施加1倍El-Centro地震波时，位移集中分布于滑体O的凸起处，最大产生3.3 m左右的永久位移。施加3倍El-Centro地震波情况下，滑体N的滑动位移显著增加，与滑体O相近。由图5（b）可见，位移较大区域分为两块，分别位于滑体N和滑体O。根据实际算例表明，随着地震动峰值的继续增大，滑体N的运动速度更快，位移更大，滑动更加剧烈。

张倬元等对于岩体边坡的滑动机制理论可以较好地解释本文的计算结果，该理论认为地震对岩体的作用主要表现在累积效应和触发效应两个方面，前者主要引起边坡岩土体结构的松动，软弱结构面错位等失稳前兆；后者主要表现在地震作用造成的边坡中软弱夹层流变和液化以及边坡瞬间失稳等。该理论与Newmark有限滑动位移理论一样，都认为地震可能造成滑坡体产生一定的永久位移，但边坡是否滑动取决于位移的大小以及岩土体内部的应力应变情况，滑动后的情况则与地形，滑体物质组成，滑体的启动条件等诸多复杂因素相关。

因此，可以认为施加1倍地震波时，滑体O的累积效应非常明显，产生较大的永久位移。一旦滑动区由累积效应过渡到触发效应后，滑体N的滑动位移显著增加，与滑体O相近。主要原因归纳为三点：

（1）整个滑坡体前缘至中部，表层组成物质主要为块碎石土；中部及后缘，表层组成物质主要为含孤石及块石较多的块碎石土、未完全解体的变质粉砂质板岩及变质细砂岩、砾岩。滑体O岩体组织较为松散，更易变形，从数值模型材料参数上来看其模量较小；

（2）滑体O位于坡面局部凸起处，其下滑坡度较缓，滑体N所处位置坡面较陡，一旦进入触发效应阶段，相同条件下其速度和位移势必更加剧烈；

（3）施加1倍El-Centro波时，滑体本身的动力反应导致滑体O的永久位移要大于滑体N。分析过程如第3节所示。

从数值分析结果看，小滑坡的稳定状态好于主滑坡。

3利用Newmark方法估计边坡动力响应对变形的影响

3.1屈服加速度的确定

根据Newmark方法，假设滑动面为圆弧形，见图6，由动力稳定系数定义，有下面两式：

本文运用自编强度折减法程序，对组成模型的所有材料的内聚力和内摩擦角进行折减，得到滑体N为最危险滑动体，其安全系数为1.4。然后保持滑体N的材料参数不变，对其他材料进行参数折减，得到最危险滑动体为滑体O，其安全系数为1.5。见图7，与动力计算得出的两个滑动危险区域相对应。

本文将两个滑体的滑动面概化为圆弧，见图8，由式（7）可分别求出其屈服加速度。

3.2滑体N和滑体O的变形情况分析

选择滑动处某点的加速度响应时程，根据Ne-wmark有限滑动位移原理，方向指向坡外，绝对值大于屈服加速度的加速度时程部分，才能产生永久位移，称为有效加速度。

图9中分别为滑体N和滑体O上某点的有效加速度时程以及由有效加速度时程二次积分求得的永久位移。计算得滑体N永久位移为2.185 m，滑体O永久位移为3.102 m。与数值模型结果符合较好。

4结语

（1）根据呷爬滑坡体的数值分析结果，在地震达到一定程度时，滑体N和滑体O将首先发生滑动，并且在1倍和3倍El-Centro波作用下具有不同的变形滑动机制：在1倍地震波作用下，滑坡体处于累积效应阶段，滑体O的永久位移较大；在3倍地震波作用下，转入触发效应阶段，滑体N的滑动速度及位移显著增加，与滑体O相近。本文分别从滑体物质组成和材料参数、滑动地形和动力响应三个方面进行了分析。从数值计算结果看，小滑坡的稳定性要好于主滑坡。

（2）本文根据Newmark有限滑动位移理论，基于滑体N和滑体O处某点的加速度响应时程，估计了滑坡体的永久位移，与数值计算结果对比符合较好。它还可以作为边坡动力响应对滑坡体影响的一个指标，可以估计地震作用对局部区域的变形影响。但必须指出，由于动力响应的非线性和共振现象，同一区域内不同点的加速度时程所产生的永久位移必然存在差异，并不是所有加速度时程都可以代表整个滑坡体进行永久位移的计算，因而，在加速度时程的选取方面还有待进一步改进。endprint