与数学知识共舞——用6种数学方法求解一道物理竞赛题

蒋金团 牛云景

(1. 云南省施甸县第一中学,云南 保山 678200; 2. 昆明市西山区第一中学,云南 昆明 650106)

·竞赛园地·

与数学知识共舞
——用6种数学方法求解一道物理竞赛题

蒋金团1牛云景2

(1. 云南省施甸县第一中学,云南 保山 678200; 2. 昆明市西山区第一中学,云南 昆明 650106)

本文用6种数学方法对2017年上海大同杯竞赛的一道物理极值题进行了求解．

导数; 物理竞赛题；动摩擦因数

数学是与物理联系最为紧密的学科之一. 很多人都说，物理学得好需要数学的辅助. 由此可见,灵活运用数学知识解决物理问题的能力在物理学习中起着非常重要的作用. 下面笔者就一道竞赛题谈谈数学知识在物理中的应用.

1 问题的提出

题目.如图1所示，质量分布均匀的直杆AB置于水平地面上,现在A端施加外力F,缓慢抬起直杆直至竖直,B端始终和地面之间保持相对静止,F的方向始终和直杆垂直,要确保直杆B端始终和地面保持相对静止,直杆和地面之间的动摩擦因数至少为多少?

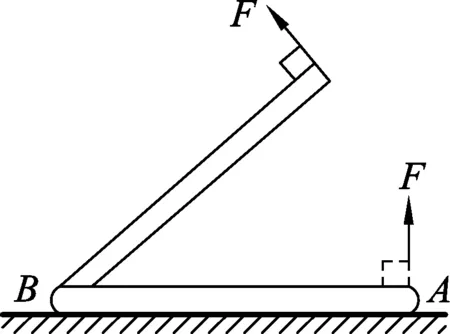
图1

解析:本题中的直杆缓慢转动,可看成是一个动态平衡问题,设直杆的长度为2L,如图2所示,对杆受力分析．由力矩平衡得

mgLcosθ=F·2L.

(1)

再根据力平衡条件,水平方向上有

μFN=Fsinθ.

(2)

竖直方向上有

FN+Fcosθ=mg.

(3)

联立(1)～(3)式得

(4)

由(4)式可知,要使B端不发生滑动,只要实际的动摩擦因素大于函数的极大值即可,这样一来,物理问题彻底转化为数学问题．

2 求极值的6种方法

2.1 导数法

对(4)式求导,有

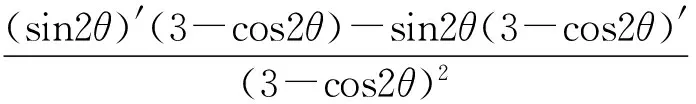
当μ′=0时,函数有极值,此时有

6cos2θ-2cos22θ-2sin22θ=0,

解得

所以

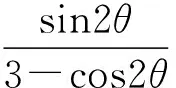
2.2 均值不等式法

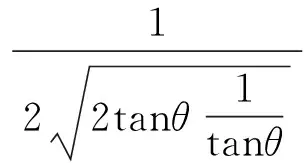
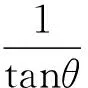
2.3 采用辅助角公式求解

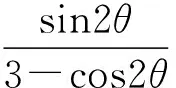
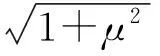
2.4 判别式法

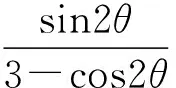
μ2(3-cos2θ)2=1-cos22θ，

化简得

(μ2+1)cos22θ-6μ2cos2θ+9μ2-1=0.

因为cos2θ有解,有

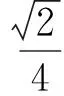
2.5 采用柯西不等式求解

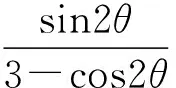
3μ=μ·cos2θ+1·sin2θ.

将上式和柯西不等式对照有

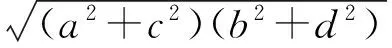
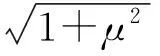
2.6 配圆法

图3

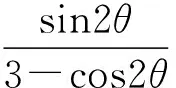
由几何关系得

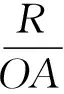
从以上解析可以看出来,物理离不开数学,只有数学才能最明确、最简洁地表达物理思想,学生的数学知识在物理课中能发挥很大的作用,把握住两门学科间的联系,有助于物理的学习．

2017-04-12)