用简谐运动的周期公式求单摆小角度摆动的周期

张晓丽

(邢台市第二中学,河北 邢台 054001)

用简谐运动的周期公式求单摆小角度摆动的周期

张晓丽

(邢台市第二中学,河北 邢台 054001)

本文首先推导质点做简谐运动的周期的一般公式,对偏角很小时单摆的振动进一步理想化,假设摆球在通过平衡位置的水平直线上往复运动．根据简化的单摆模型求出: (1) 做固有振动的单摆； (2) 匀加速上升(或下降)的电梯中的单摆； (3) 在匀强电场或匀强磁场中的单摆的回复力比例系数,再由简谐运动的周期公式求出这几种单摆的周期,不需要引入等效重力加速度和等效摆长的概念．

简谐运动的周期; 简化的单摆; 回复力比例系数; 小角度摆动

单摆是简谐运动的理想化模型之一,我们遇到求单摆振动周期问题时,总是借助等效重力加速度和等效摆长两个物理量．通过对单摆做简谐运动的进一步简化,根据简谐运动的一般周期公式可以求各类单摆小角度摆动的周期．

1 简谐运动的周期公式

图1

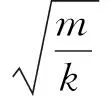
(1)

(1)式中k是回复力与位移关系式的比例系数,该式是简谐运动的一般周期公式．

2 单摆小偏角摆动的进一步理想化

摆球静止在最低点O时,摆球受到的重力mg和悬线的拉力T平衡,小球受合力为0,O点为单摆的平衡位置,拉开摆球使它偏离平衡位置,放手后摆球以平衡位置为中心做往复运动．[1]偏角越小,摆球沿圆弧运动过程中的竖直分位移越小,当偏角很小时设想将摆球的竖直位移忽略不计,认为小球在通过平衡位置O的水平线上左右做简谐运动．单摆做固有振动时竖直方向处于平衡状态合力为0,做其他振动时若有竖直加速度则该方向遵循牛顿第二定律,回复力是摆线张力的水平分力,在匀强磁场中的单摆的回复力是张力T与洛仑兹力f合力的水平分力．这是对单摆做简谐运动条件的进一步理想化,我们称它为简化的单摆．

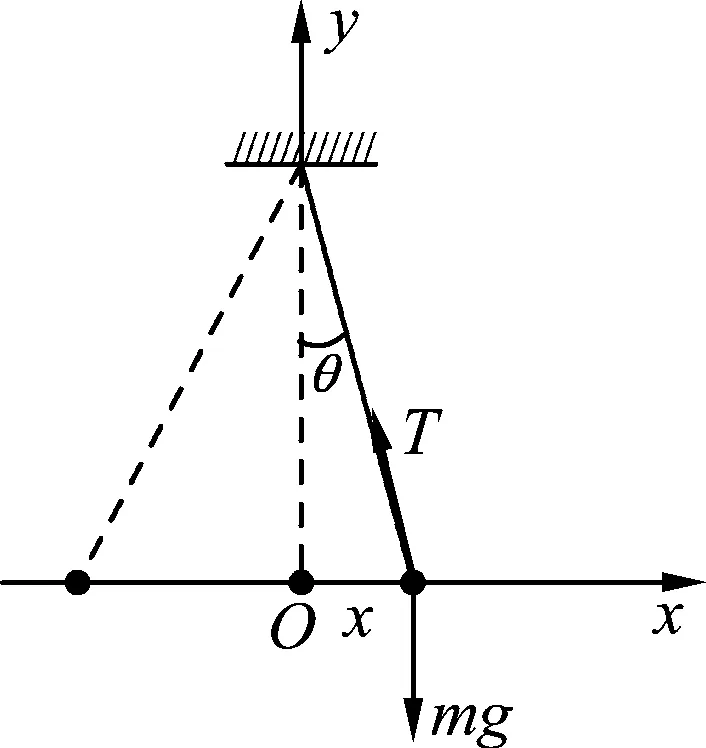
图2

(2)

3 单摆做固有振动的周期

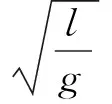
(3)

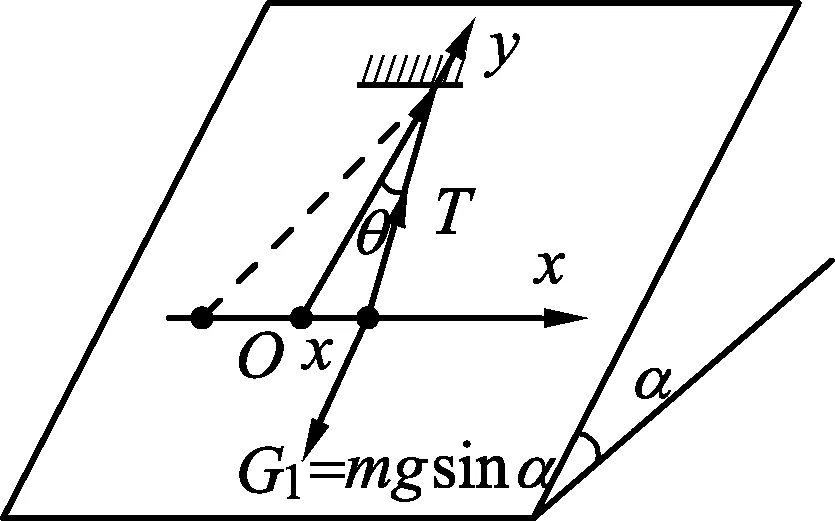
图3

例1.如图3所示,光滑斜面上的摆球,斜面倾角为α,摆线长为l,求摆球在平衡位置附近来回振动的周期.

解析：摆球受3个力:重力mg,细线的拉力T,斜面的支持力N(图3中只画出光滑斜面内所受的力),小球做小角度摆动时,在y方向上,根据平衡条件,得Tcosθ=mgsinα,在x方向上,回复力为F=-Tsinθ=-mgsinαtanθ,由此可得

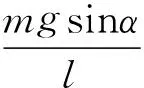
(4)

(5)

例2.如图4所示,已知地球半径为R,地球表面的重力加速度为g,在距地球表面高度h(h≪R)处有一个单摆,求摆球在平衡位置附近来回振动的周期.

解析：设在离地面h高度处重力加速度为g1,摆球受两个力:重力mg1和细线拉力T,小球做小角度摆动时,在y方向上Tcosθ=mg1,在x方向上,回复力为

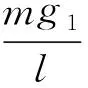
(6)

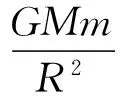
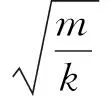
(7)

4 匀加速上升(或下降)的电梯中单摆的振动周期

例3.如图5所示,电梯以加速度a匀加速上升,在电梯中有一个单摆做小角度摆动,重力加速度为g,求单摆的运动周期.

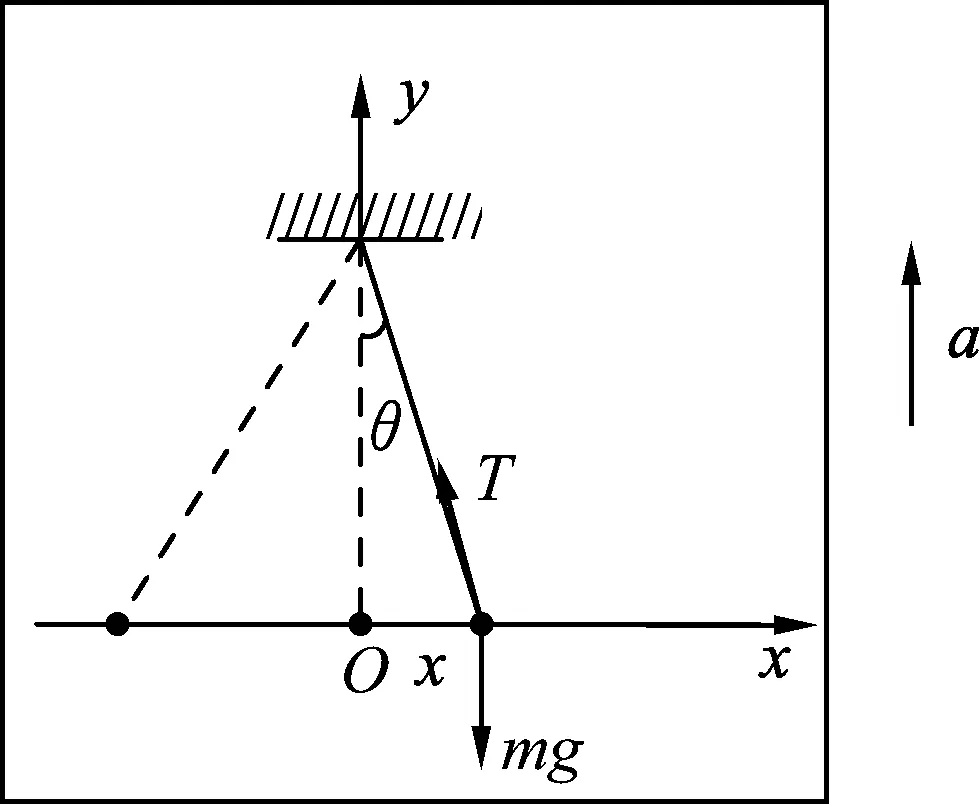
图5

解析：摆球受两个力作用:重力mg和细线的拉力T,摆球随电梯以相同的加速度向上做匀加速直线运动,小球做小角度摆动时,在竖直方向上,根据牛顿第二定律,[2]得Tcosθ-mg=ma,在水平方向上,回复力为F=-Tsinθ,由此可得

(8)

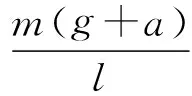
(9)

5 在匀强电场或匀强磁场中单摆的周期

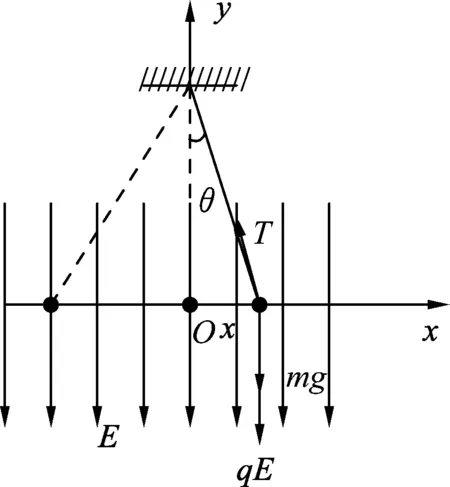
图6

例4.如图6所示,竖直向下的匀强电场的电场强度为E,绝缘细线的一端固定,另一端系一个小球,小球所带电荷量为+q,使小球在匀强电场中做小幅度摆动,求小球的摆动周期.

解析：小球在摆动过程中受3个力作用:重力mg,竖直向下的电场力qE和细线的张力T．小球做小幅度摆动时,在竖直方向上,根据平衡条件,得Tcosθ=mg+qE,在水平方向上,回复力为F=-Tsinθ,由这两式解得

(10)

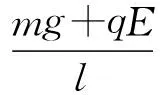
(11)

图7

例5.如图7所示,在垂直于纸面向里的匀强磁场中,绝缘细线的一端固定, 另一端系一个带电小球,小球带电荷量为+q,匀强磁场的磁感应强度为B,求小球做小角度摆动时的周期.

解析：小球在运动过程中受3个力:重力mg,细线的拉力T和洛仑兹力f,f=Bqv．下面分两种情况求回复力．

小球从右向左摆动过程中,根据左手定则,洛仑兹力f沿细线向下,与拉力T方向相反,如图7所示.小球做小角度摆动时,在竖直方向上,根据平衡条件,Tcosθ=mg+fcosθ,即(T-f)cosθ=mg,在水平方向上,回复力为F=-Tsinθ+fsinθ，即F=-(T-f)sinθ,根据这两式,解得

小球从左向右摆动过程中,根据左手定则,洛仑兹力f沿细线向上,与拉力T方向相同,同理,可得

(12)

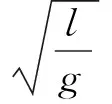
(13)

上面我们运用简谐运动的周期和简化的单摆这个理想化模型,针对几种常见的单摆,推导了它们的回复力表达式,求出它们做简谐运动的周期．这种方法的思路是:分析摆球的受力情况,在满足小角度摆动的条件下,运用平衡条件或牛顿第二定律求出回复力表达式从而确定比例系数k,再根据简谐运动的周期公式求单摆的周期．等效法虽然普遍地用来求单摆的周期,但总使人感到缺乏依据,不知道遵循的是什么物理规律．我们提出的求单摆周期的方法,是对单摆运动过程的理想化,较好地反映了单摆的运动特征,使人们比较透彻地理解单摆的周期的概念,而且也可以求任何单摆做简谐运动的周期．

1 人民教育出版社.普通高中课程标准实验教科书物理选修3-4[M].北京:人民教育出版社,2010:13-16.

2 柯尧.赏析一道求振动周期的竞赛题的多种解法[J].物理教师,2016,37(10):92-93.

2017-03-12)