一族可积的非线性晶格方程

(山东科技大学数学与系统科学学院 山东 青岛 266590)

一族可积的非线性晶格方程

姜鹏飞

(山东科技大学数学与系统科学学院山东青岛266590)

孤立子理论的研究不断发展，在很多科学领域都存在孤立子以及与孤立子理论密切联系的问题，本文引入一个离散的特征值问题，导出一族离散的可积系。

离散谱问题；离散可积系

一、引言

离散可积系统与辛算法、DNA的研究以及元胞自动机等有着密切的联系，有着十分广阔的应用前景，因此，离散可积系统的研究引起了广大的关注，许多离散可积系已经被系统地研究[1-7]。本文引入一个离散的矩阵谱问题，通过离散的零曲率方程，导出了一族离散可积系。

二、离散可积系的导出

首先，我们引入下列离散的谱问题

(1)

其中E是位移算子，其逆及差分算子的定义如下：

(Ef)(n)=f(n+1),(E-1f)(n)=f(n-1),n∈Z,

(2)

(Df)(n)=f(n+1)-f(n)=(E-1)f(n),n∈Z,

(3)

并且记f(j)=Ejf,j∈Z.假设p=p(n,t),q=q(n,t)是定义在Z×R上的实函数。λ是谱参数并且λt=0.

为了得到离散的可积系，我们首先解离散的谱问题(1)的驻定的离散零曲率方程(EΓ)U-UΓ=0,

(4)

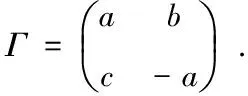
容易验证(4)的四个分量方程为

λ2(a(1)-a)+b(1)q-λ2cp=0,λ2p(a(1)+a)+b(1)-λ2b=0,λ2c(1)-c-q(a(1)+a)=0,λ2pc(1)-qb-(a(1)-a)=0.

(5)

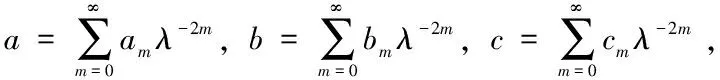
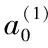
(6)

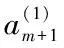
(7)

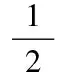
bo=-p,a1=pq(-1),b1=-p(1)-p2p(-1)+pp(1)q,c1=-q(-1),

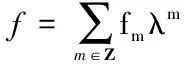
容易验证

(E(Γλm)+)U-U(Γλm)+

为了得到离散的可积系，选择附加项

并且令Vm=(Γλm)++Δm，则离散的零曲率方程

Utm=(EVm)U-UVm,m≥0,

(8)

等价与以下的离散的非线性可积系统

ptm=bm-vam,qtm=-wam-cm.

(9)

当m=1时，得到(9)中一组非线性可积系统

pt1=(pq-1)p(1),qt1=(1-pq)q(-1).

[1]Ablowitz M J and Ladik J F.Nonlinear differential-deference equation[J].J.Math.Phys,1975,16:598-603.

[2]Tu Gui-Zhang.A trace identity and its applications to the theory of discrete integrable systems[J].J.phys.A:Math,Gen,1990,23:3903-3922.

[3]Ma Wen-Xiu,Xu Xi-Xiang.Positive and negative hierarchies of integrable lattice models associated with a Hamiltonian pair[J].International Journal of Theoretical Physics,2004,43:219-236.

[4]Ma Wen-Xiu,Xu Xi-Xiang.A modified Toda spectral problem and its hierarchy of bi-Hamiltonian lattice[J].J.phys.A:Math.Gen,2004,37:1323-1336.

[5]Xu Xi-Xiang,Zhang Yu-Feng.A hierarchy of Lax integrable lattice equations,Liouville integrability and a new integrable symplistic map[J].Commun.Theor.Phys.(Beijing,China),2004,41:321-328.

[6]Wu Yong-Tang,Geng Xian-Guo.A new integrable symplectic map associated with lattice soliton equations[J].J.Math.Phys,1996,37:2338-2345.

[7]Cao Ce-Wen,Geng Xian-Guo,Wu Yong-Tang.From the special 2+1 Toda lattice to the Kadomtsev-Petvashvili eqution[J].J.Phys.A:Math.Gen,1999,32:8059-8078.

姜鹏飞，男，汉族，山东潍坊，硕士研究生，山东科技大学，计算理论与数据处理。