基于因子分析的大学生创新素质影响因素
向 莹
(常州机电职业技术学院 文化基础部,江苏 常州 213164)
基于因子分析的大学生创新素质影响因素
向 莹
(常州机电职业技术学院 文化基础部,江苏 常州 213164)
为了给高校培养大学生创新素质提供一定的依据,也为了给高校技能大赛挑选参赛选手提供参考,通过因子分析对影响大学生创新素质的因素进行研究,得到创新能力因子是第一个公因子,并且可以运算得到大学生创新素质的综合得分。
大学生创新素质;影响因素;因子分析
国际上认为较早提出创新理论的是经济学家、哈佛大学教授约瑟夫·熊彼特(Joseph A.Schumpeter,1883—1950年),1912年他在《经济发展理论》一书中运用创新理论解释了发展的概念[1]。创新素质是指人在先天遗传素质基础上后天通过环境影响和教育所获得的稳定的在创新活动中必备的基本心理品质与特征[2]。习近平总书记在参加十二届全国人大三次会议上海代表团审议时强调:“创新是引领发展的第一动力。抓创新就是抓发展,谋创新就是谋未来。适应和引领我国经济发展新常态,关键是要依靠科技创新转换发展动力”。大学生作为国家的希望和未来,其创新素质的培养是非常必要的。因此对影响大学生创新素质的因素进行因子分析,是高校培养大学生创新素质的首要任务。
1 因子分析
1.1因子分析的基本思想
因子分析的思想起源于1904年斯皮尔曼发表的文章《对智力测验得分进行统计分析》 ,也是一种降维、简化数据的技术。因子分析的基本思想是根据原始变量相关性大小进行分组,使得同组内的变量之间相关性较高,而不同组的变量间的相关性则较低。每组变量代表一个基本结构,并用一个不可观测的综合变量表示,这个基本结构就称为公共因子。对于所研究的某一具体问题,原始变量就可以分解成两部分之和的形式,一部分是少数几个不可测的所谓公共因子的线性函数,另一部分是与公共因子无关的特殊因子。
1.2因子分析的数学模型
设有n个样本,每个样本有m个指标,且这m个指标之间存在显著的相关关系。在进行因子分析之前首先要求对数据进行标准化处理,标准化后每个变量均值为0,方差为1。因子分析中的公共因子是不可直接观测但又客观存在的共同影响因素,每一个变量都可以表示成公共因子的线性函数与特殊因子之和,即
这就是因子分析的数学模型,用矩阵形式表示为
X=ΛF+ε,

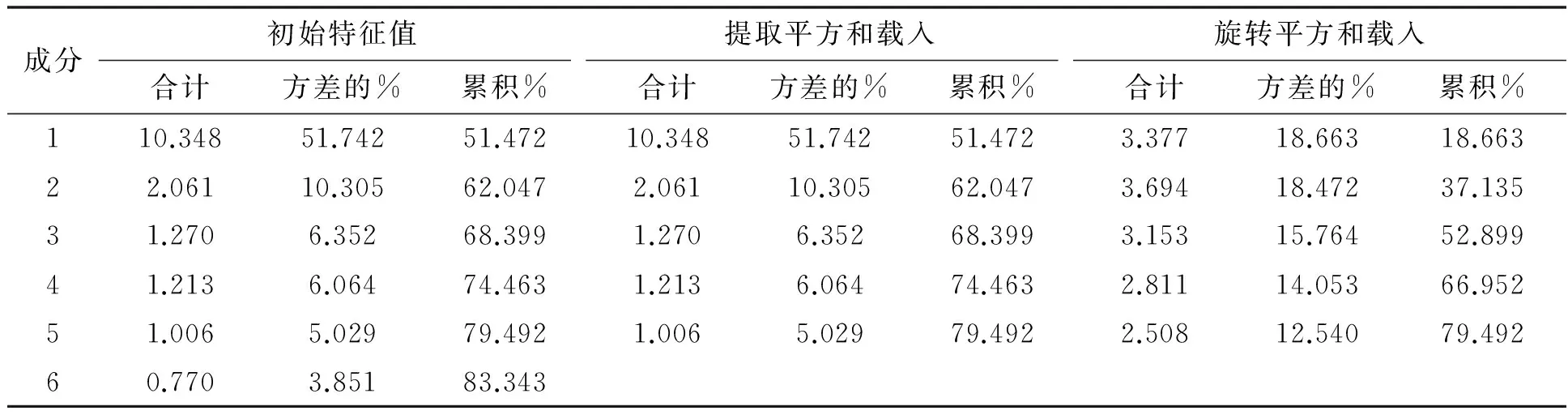
1)m 2)协方差cov(F,ε)=0,即公共因子与特殊因子之间不相关; 3)各个公共因子不相关且方差为1; 4)各个特殊因子不相关,方差不要求相等[3]。 2.1调查问卷设计 根据创新素质的内涵编制了此次研究所用的调查问卷表(见表1),并采用完全具有为5分;具有为4分;一般为3分;较少为2分;没有为1分的5级计分制进行统计。 2.2数据分析 2.2.1 因子分析的适用性检验 对某专业某班45名学生进行了问卷调查,收回有效问卷45份。本次问卷调查采用不记名方式,因此调查结果具有较高的真实性,所以对调查结果进行统计分析是有意义的。运用SPSS软件对调查统计数据进行KMO和Bartlett球形度检验,得到KMO统计量为0.831,sig.小于0.05,表明变量间的偏相关性较好,也即调查问卷统计的数据适合做因子分析。 2.2.2 确定公因子个数 运用SPSS软件,提取方法选择主成分分析法,得到解释的总方差及公因子方差。第一成分的初始特征值为10.348,远远大于1;第二成分的初始特征值为2.061,大于1;第三成分的初始特征值为1.270,大于1;第四成分的初始特征值为1.213,大于1;第五成分的初始特征值为1.006,大于1。因此选择5个公共因子可得到79.492%的累计方差贡献率,表示5个公共因子可以解释约79%的总方差。并且还发现上述20个变量的共性方差均大于0.5,表示5个公共因子能很好地反映原始变量的信息;结合碎石图发现前5个公因子变化较大。因此选择5个公因子结果还是比较理想的。 表1 调查问卷表(部分) 2.2.3 因子旋转 为了进一步确定每个公因子的意义,需要进行因子旋转。运用最大方差法得到因子旋转结果(见表2、表3)。由旋转成分矩阵可以看出,第一个公因子在变量X14、X15、X16、X19、X20上具有较大的载荷,第二个公因子在变量X1、X3、X4、X5上具有较大的载荷,第三个公因子在变量X7、X8、X10上具有较大的载荷,第四个公因子在变量X11、X12、X13上具有较大的载荷,第五个公因子在变量X5、X6上具有较大的载荷。按照每个变量对应的具体内容,第一个公因子可以定义为“创新能力因子”,第二个公因子和第四个公因子可以定义为“创新知识和品质因子”,第三个公因子可以定义为“创新精神因子”,第五个公因子可以定义为“创新思维因子”。由旋转后解释的总方差结果可以得出,第一个公因子的贡献率为18.663%,第二个公因子和第四个公因子的贡献率为32.525%,第三个公因子的贡献率为15.764%,第五个公因子的贡献率为12.540%。 表2 旋转成分矩阵 表3 旋转后解释的总方差 2.2.4 因子得分 将调查问卷中各项目的得分依次用变量X1~X20表示,在因子旋转的基础上,再运用SPSS软件计算得到因子得分如下。 F1=-0.059X1-0.227X2-0.011X3-0.116X4-0.066X5+ 根据以上公式,可以计算出每位学生五个公因子的得分。再由旋转后解释的总方差这张表中可以得到F1,F2,F3,F4,F5的权重,进而得出学生创新素质的综合得分公式为 F=18.663%F1+18.472%F2+15.764%F3+14.053%F4+12.540%F5, 根据公式可以计算每位学生的创新素质综合得分并可进行排名,这也能为高校技能大赛挑选参赛选手提供参考依据。 根据因子分析结果发现,在影响大学生创新素质因素中,“创新能力因子”的影响权重是最大的,其次是“创新知识和品质因子”,再次是“创新精神因子”,最后则是“创新思维因子”。这无疑能为高校在大学生创新素质培养方面提供一定的依据。 [1] 杨向荣等.大学生创新实践指导[M].北京:冶金工业出版社,2011. [2] 朱琼瑶.创新素质的结构刍议[J].大连教育学院学报,2002,18(2):23-24. [3] 李春林,陈旭红.应用多元统计分析[M].北京:清华大学出版社,2013. InfluenceFactorsofInnovationCapacitiesofCollegeStudentsBasedonFactorAnalysis XIANG Ying (Department of Culture Fundamentals, Changzhou Vocational Institute ofMechatronic Technology, Changzhou 213164, Jiangsu, China) Innovation is the driving force of social development. Higher education is committed to developing the innovation capacities of college students. In order to provide a basis for improving college students’ innovative quality, and to offer a reference for selecting competitors in skills competition, by using the methods of factor analysis, we studied the influence factors of innovation capacities of college students, and made our conclusion that the innovation capacities as the common divisor comes out top of the list. Meanwhile, comprehensive results of college students’ innovation capacities are developed. They are presented to offer a useful reference for colleges when choosing contestants in technical and skill tests, and a support for expanding the innovation capacities of college students. innovation capacities of college students; influence factors; factor analysis G645 A 1008-9446(2017)04-0067-04 2015年江苏省高等教育教改研究立项课题(基于创新素质培养的高职数学教学改革的研究与实践):2015JSJG530 2017-01-06 向莹(1981-),女,江苏常州人,讲师,硕士,主要从事高职数学教育,E-mail:xiangyingkelly@163.com。2 创新素质研究


0.022X6+0.002X7-0.166X8+0.015X9-0.169X10-
0.185X11+0.025X12+0.027X13+0.304X14+0.322X15+
0.263X16+0.098X17-0.009X18+0.224X19+0.309X20
F2=-0.240X1+0.094X2+0.311X3+0.320X4+0.275X5-
0.122X6-0.126X7+0.017X8-0.036X9+0.193X10+
0.193X11-0.151X12-0.197X13-0.092X14-0.099X15+
0.055X16-0.061X17+0.021X18-0.058X19-0.079X20
F3=-0.091X1-0.131X2-0.063X3-0.032X4-0.012X5+
0.065X6+0.403X7+0.396X8+0.182X9+0.313X10-
0.034X11-0.089X12-0.042X13-0.198X14+0.086X15-
0.069X16-0.106X17-0.051X18+0.233X19-0.094X20
F4=-0.114X1-0.033X2-0.008X3+0.009X4-0.048X5-
0.063X6-0.033X7-0.009X8-0.200X9-0.011X10+
0.466X11+0.382X12+0.276X13+0.018X14-0.138X15-
0.032X16-0.044X17+0.261X18-0.121X19+0.126X20
F5=0.166X1+0.521X2-0.127X3-0.036X4-0.007X5+
0.305X6-0.120X7-0.067X8+0.215X9-0.182X10-
0.294X11+0.041X12+0.150X13+0.094X14-0.073X15-
0.123X16+0.327X17-0.031X18-0.185X19-0.136X203 结束语

