基于偏态分布的轶纶®短纤维拉伸性能及细度概率分布
刘 超,汪泽幸,李洪登,彭新元,李文辉
(1. 湖南工程学院 纺织服装学院, 湘潭 411104;2.湖南永霏特种防护用品有限公司, 湘潭 411104)
基于偏态分布的轶纶®短纤维拉伸性能及细度概率分布
刘 超1,汪泽幸1,李洪登1,彭新元1,李文辉2
(1. 湖南工程学院 纺织服装学院, 湘潭 411104;2.湖南永霏特种防护用品有限公司, 湘潭 411104)
为进一步研究聚酰亚胺纤维的力学性能,以轶纶®短纤维为研究对象,对其拉伸性能及细度指标进行了实验测试,并对各指标的分布进行了统计学分析.试验结果表明,纤维的拉伸性能及细度指标均呈现偏态分布特征,纤维的强力与伸长率均可用三参数Weibull分布来描述,而纤维的线密度与细度均可用三参数Log-logistic分布来描述.同时发现,纤维的强力与伸长率之间存在弱相关性(R2=0.49).可靠性分析表明,在同等累计分布概率(0.5)下,强力和伸长率的理论计算值高于算数均值,而纤维线密度和直径的计算值低于算数均值.
聚酰亚胺(PI);短纤维;强力;伸长率;线密度;纤维直径;偏态分布
作为主链上含有酰亚胺环的一类高性能聚合物,聚酰亚胺(PI)具有良好的热氧化稳定性,优异的机械性能、耐辐射性能及绝缘性能[1].相比于芳纶、聚苯硫醚等纤维,PI具有较好的综合应用性,已成为当前高技术纤维的重要品种之一,在航空航天、环保、防火等应用领域需求迫切[2-4].
通常所谓的纤维强力是测试结果的平均值,其建立在纤维强力服从于正态分布的基础之上的;纤维强度也是强力与平均细度的比值.在纤维加工和使用过程中,由于其内部和表面随机分布的缺陷,会直接影响纤维的力学性能,而呈现出一定的离散程度;同时,在纺丝过程中,受到纺丝原料性能波动性和工艺参数的波动性的影响[5],纤维细度也呈现一定的波动变化,而呈现一定的统计分布特性.
目前,通常采用正态分布(又称高斯、常态分布)、指数分布、S分布、Weibull分布来描述纤维的强力或强度的离散程度[6-10],这主要是考虑到上述分布模型参数估计和置信度的方便性.现有研究结果表明Weibull分布模型,特别是三参数Weibull分布模型较适宜描述纤维强力或强度的分布特征.
纤维细度作为纤维的重要指标之一,其将影响最终产品的耐穿性,舒适性和质量.特别是在羊毛质量的测定中,除纤维平均细度外,纤维细度分布是最为重要的.成纱条干的不匀率不仅仅受纤维细度的影响,同时还受细度离散程度的影响.目前,对纤维细度的离散型及统计模型研究较少,贾迎宾等[11-13]对山羊绒[11-12]、羊毛[13]细度的分布频率进行了分析,但未就分布模型进行讨论.
基于此,本文基于轶纶®短纤维,选用断裂强力和断裂伸长率为强伸性能指标,以线密度和纤维直径为细度指标,对其强伸性能和细度进行试验测定,采用偏态分布模型对其性能指标的离散程度进行统计学描述.
1 实验对象及方法
1.1 实验样品
本文以长春高崎聚酰亚胺材料有限公司生产的轶纶®短纤维为实验对象,短纤维的线密度为2.22 dtex(2 Denier).
1.2 纤维强度
参考GB/T14337-2008在XQ-1型纤维强度仪上对纤维的拉伸强力进行测试,预加张力为0.35 cN,夹持隔离为20 mm,加载速度为40 mm/min,有效样品数量为100.在测试过程中,记录各根纤维的强力、伸长率.
1.3 纤维线密度
参考GB/T16256-2008,在XD-1型振动式纤维细度仪上进行纤维线密度测试,夹持隔离为20 mm,预加张力为0.35 cN,有效样品数为100.
1.4 纤维直径
参考GB/T 20732-2006在CU-2纤维细度仪上对纤维直径进行测定,有效测试次数为100次.

2 测试与统计结果分析
2.1 试验结果分析
试验用轶纶®纤维的强力、伸长率、线密度及纤维直径分布频数绘于图1~图4中.
从图1~图4中可以看出,纤维的强力、伸长率、线密度及直径均存在一定的离散性,各项指标之间的变异系数均超过5%,其中,强力变异系数接近10%,伸长率的变异系数接近15%.从极差角度而言,极差系数均超过了29%,性能指标离散明显;因而在纤维性能表征时,仅考虑平均值是不全面的,需对其指标的离散程度和模型进行统计分析.
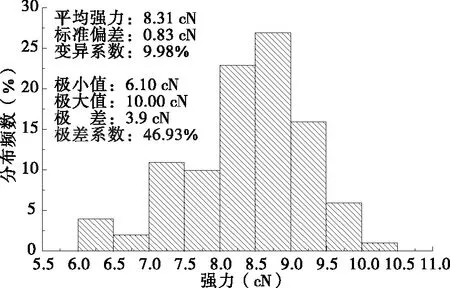
图1 纤维强力频率分布

图2 伸长率频率分布
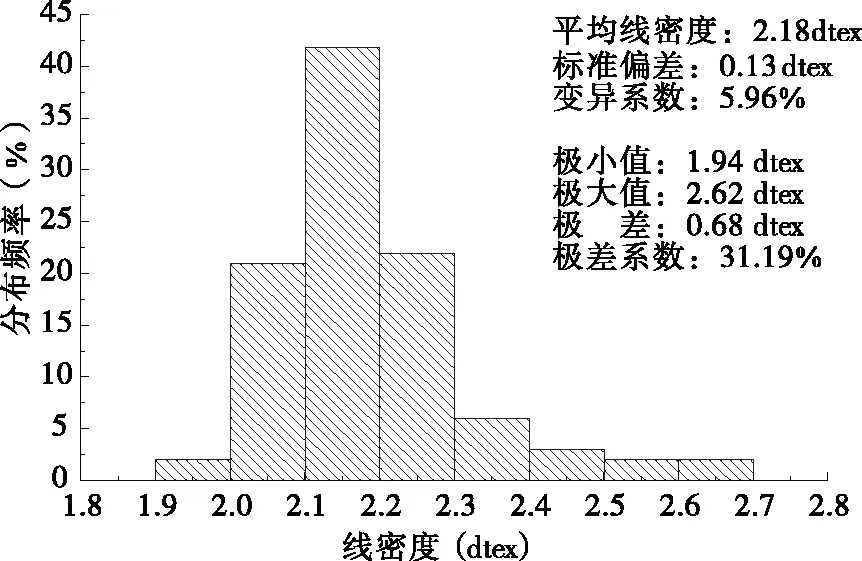
图3 纤维线密度频率分布
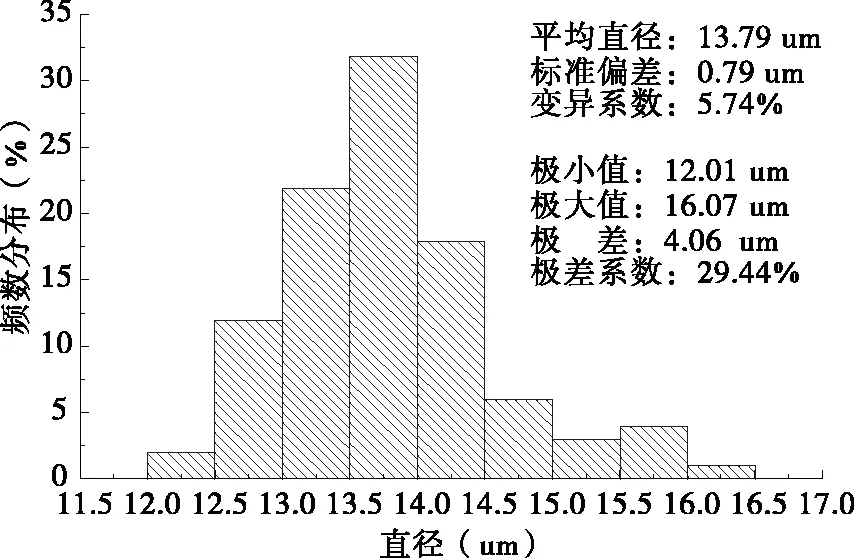
图4 纤维直径频率分布
2.2 统计分布模型及检验
2.2.1 统计分布模型
从图1~图4中可以看出,纤维各项指标的频率分布中,多数频数不集中在中央位置,即性能指标的分布不呈正态分布,而呈偏态分布.其中纤维强力与伸长率的频数分布集中位置偏向右侧,呈现负偏态分布;而线密度与直径的频数分布集中位置偏左,呈现正偏态分布.
基于纤维性能指标的偏态分布特性,本文选用对数正态(Log-normal)分布、韦伯尔(Weibull)分布以及对数逻辑斯谛克(Log-Logistic)分布对实测数据进行分布拟合和分析.
当变量x服从于对数均值为μ,对数标准差为σ,位置参数为γ的三参数Log-normal分布时,其概率密度函数f(x)及累计分布函数F(x)可表示为:
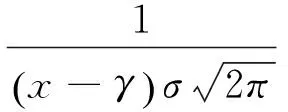
(1)
(2)
式中,0<γ≤x<∞,Φ为拉普拉斯算子.
当位置参数γ=0时,三参数log-normal分布简化为两参数Log-normal分布,其概率密度函数f(x)及累计分布函数F(x) 可表示为:
(3)
(4)
当变量x服从于形状参数为α,尺度参数为β,位置参数为γ的三参数Weibull分布时,其概率密度函数f(x)及累计分布函数F(x)可表示为:
(x>0)
(5)
(6)
其中:γ为位置参数,0<γ≤x<∞;α、β>0.
对于三参数Weibull分布中,位置参数γ=0时,其简化为两参数Weibull分布,其概率密度函数f(x)及累计分布函数F(x)可表示为:
(7)
(8)
当变量x服从于形状参数为α,尺度参数为β,位置参数为γ的三参数Log-logistic分布时,其概率密度函数f(x)及累计分布函数F(x)为:
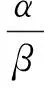
(9)
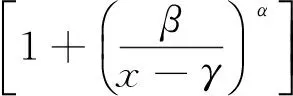
(10)
其中:γ为位置参数,0<γ≤x<∞;α、β>0.
当三参数Log-logistic分布中,γ=0时,其简化为两参数Log-Logistic分布,其概率密度函数f(x)及累计分布函数F(x)可表示为:
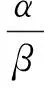
(11)
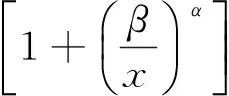
(12)
2.2.2 分布模型的参数估计与拟合优度的检验
目前,分布模型的参数通常采用专业软件来实现估计.本文以实测值为基础,采用Easyfit 5.6对分布函数进行拟合.为判断样本来自的总体是否服从某一指定分布,以“K-S”检验法对分布模型进行检验.
单样本“K-S”检验原假设H0为样本来自的总体与指定的理论分布无显著性差异;在原假设成立的前提下,基于估计的参数获得理论累计概率分布F(x);基于样本数据计算各样本数据点的累计概率,得到检验累计概率分布函数S(x),计算F(x)与S(x)差序列D(x),获得差值序列中的最大绝对差值D=max(|S(xi)-D(xi) |);如果样本总体的分布与理论分布差异不明显时,则D值应较小,反之样本总体分布与理论分布差异较大.
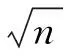
2.3 强伸性能分布及其相关性
纤维强力及伸长实测数据基于Log-normal分布、Weibull分布及Log-logistic分布进行分布拟合,拟合参数及P值列于表1和表2中.
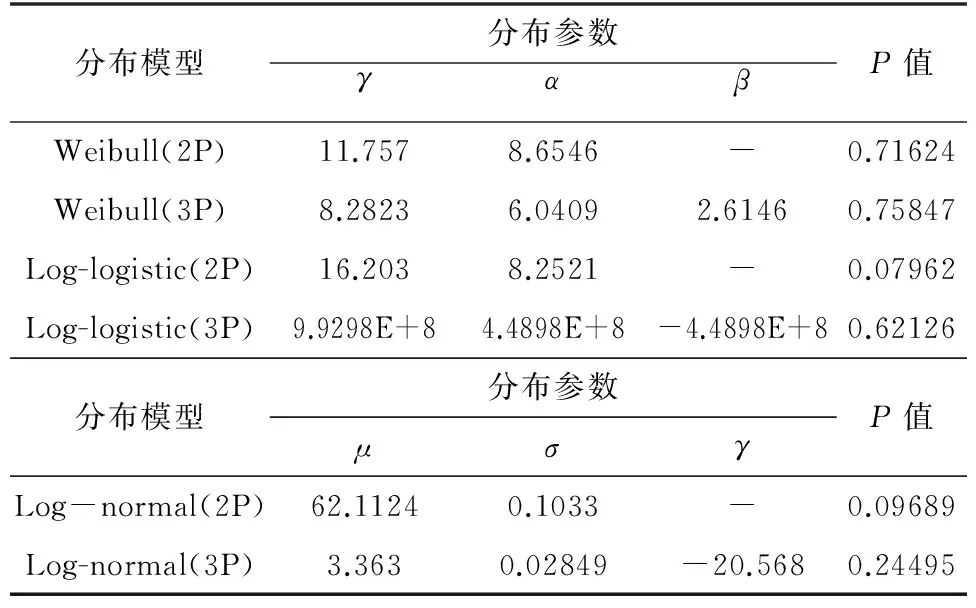
表1 强力分布参数估计
从表1和表2中可以看出,因Log-normal(3P)和Log-logistic(3P)分布的拟合参数中,位置参数γ<0,可认为强力及伸长分布不符合Log-normal(3P)和Log-logistic(3P)分布;对比分析各分布模型拟合获得的P值发现,相对于Weibull分布,Log-normal (2P)和Log-logistic(2P)分布的P值较小,且Weibull (2P)与Weibull (3P)分布的P值较高且接近,故可认为纤维强力和伸长率统计分布形式可用Weibull分布来描述,其中Weibull (3P)分布模型较佳.
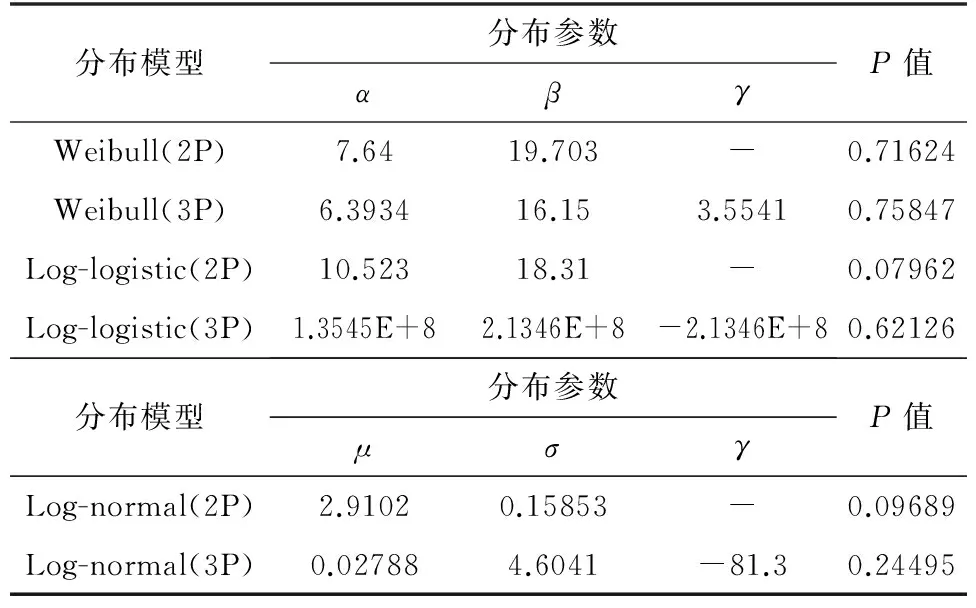
表2 伸长率分布参数估计
杨萍等[15]研究发现羊毛束纤维强力与伸长率之间存在一定的相关性(相关系数R2=0.53),基于此,为分析轶纶®短纤维强力与伸长率之间的相关性,其拉伸强力与伸长率之间的关系及拟合直线汇于图5中.分析结果表明,轶纶®短纤维的强力与伸长率之间的相关系数R2为0.49,表明轶纶®纤维的强力与伸长率之间存在一定的相关性,但相关性不强,即呈现弱相关性.
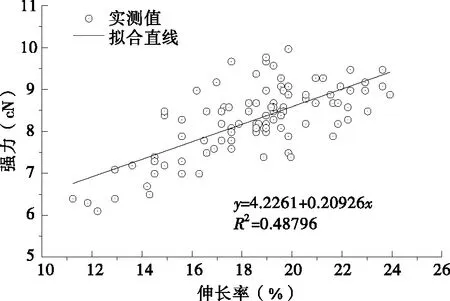
图5 强力与伸长相互关系
2.4 纤维细度分布
纤维线密度及直径的实测数据基于Log-normal分布、Weibull分布及Log-logistic分布进行分布拟合,拟合参数及P值列于表3和表4中.
从表3可以看出,Weibull(3P)、Log-logistic(2P)、Log-logistic(3P)及Log-normal(3P)分布的P值均超过0.05,可认为,这四种分布均可用于描述轶纶®纤维的线密度分布,但Log-logistic(3P)的预测精度最高.
从表4中可以看出,上述分布模型的P值均大于0.05,可认为上述分布模型均可用于描述轶纶®短纤维的直径分布;Log-logistic分布模型的P值较高,均超过0.81,其中Log-logistic(3P)分布模型的P值超过0.85,因此基于P值的判定,可认为轶纶®短纤维的直径分布采用Log-logistic(3P)分布模型较为适宜.
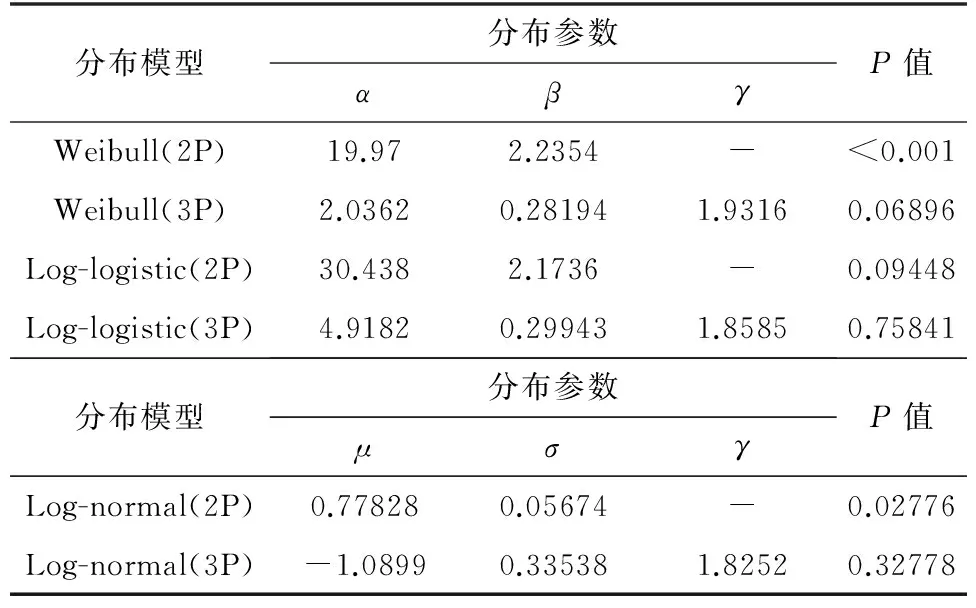
表3 线密度分布参数估计
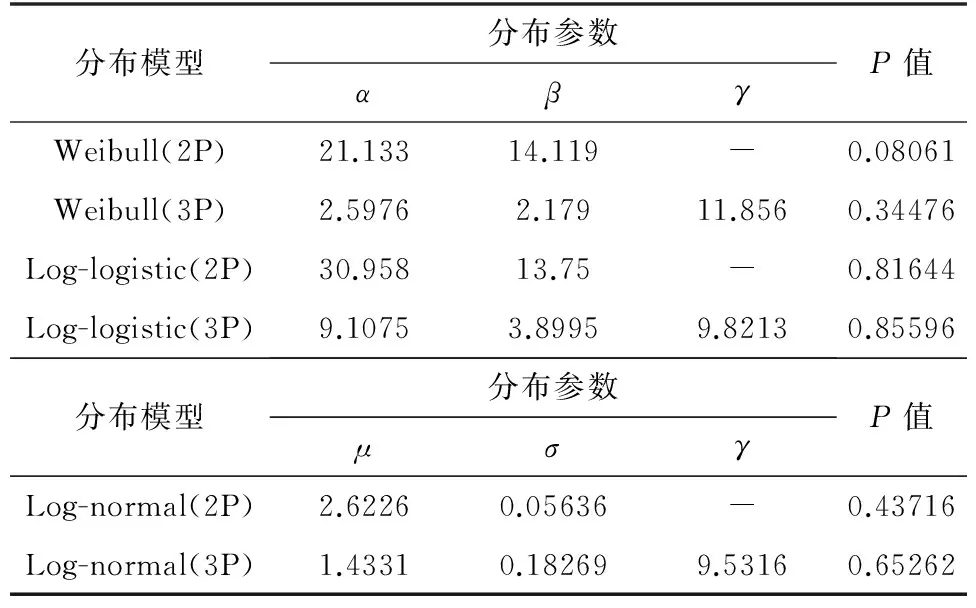
表4 纤维直径分布参数估计
2.5 可靠性分析
2.3和2.4的分析结果表明,在选用的3种6类偏态分布模型中,轶纶®短纤维的强力和伸长率统计分布采用Weibull分析模型较为合理,其中Weibull(3P)分布模型最佳;而轶纶®短纤维线密度和纤维直径采用Log-logistic分布较为合理,其中Log-logistic(3P)分布最佳.
当变量呈正态分布时,平均值对应的累积概率为0.5,即表明变量值小于或大于平均值的概率为50%.基于此,基于较优的分布模型,计算累计概率F(x) =0.5时的性能指标值,计算值列于表5中.
从表5中可以看出,在同等累积概率条件下,对于强力和伸长率,Weibull分布计算值高于算术平均值,且Weibull(3P)计算值较高,表明采用算术均值来表征纤维强力较为保守;对于线密度和纤维直径,Log-logistic计算值较算术均值低,其中,Log-logistic(3P)的计算值最低,表明采用算术均值来表征纤维的线密度和直径较冒进.
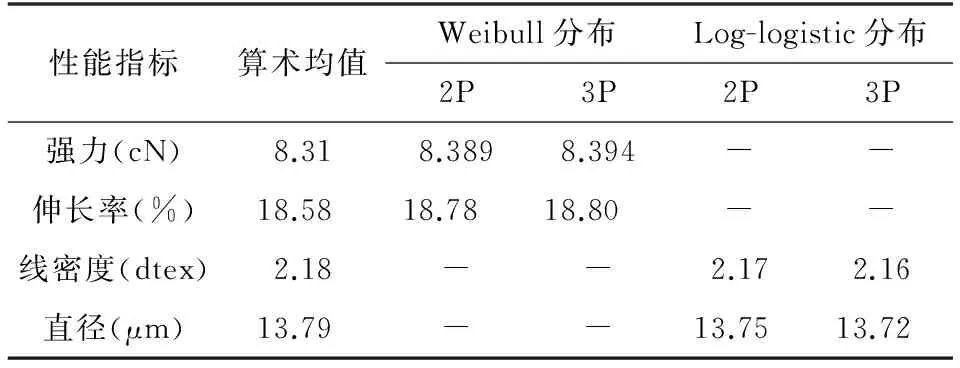
表5 累计概率为0.5时分布模型计算值对比
注:采用Weibull(2P)与Weibull(3P) 计算的强力和伸长率相近,为比较两者的差异,故取三位小数表示.
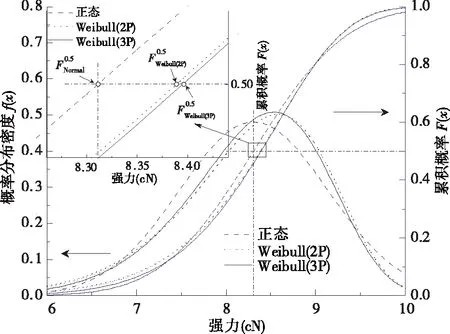
图6 强力计算值对比分析(F(x) =0.5)
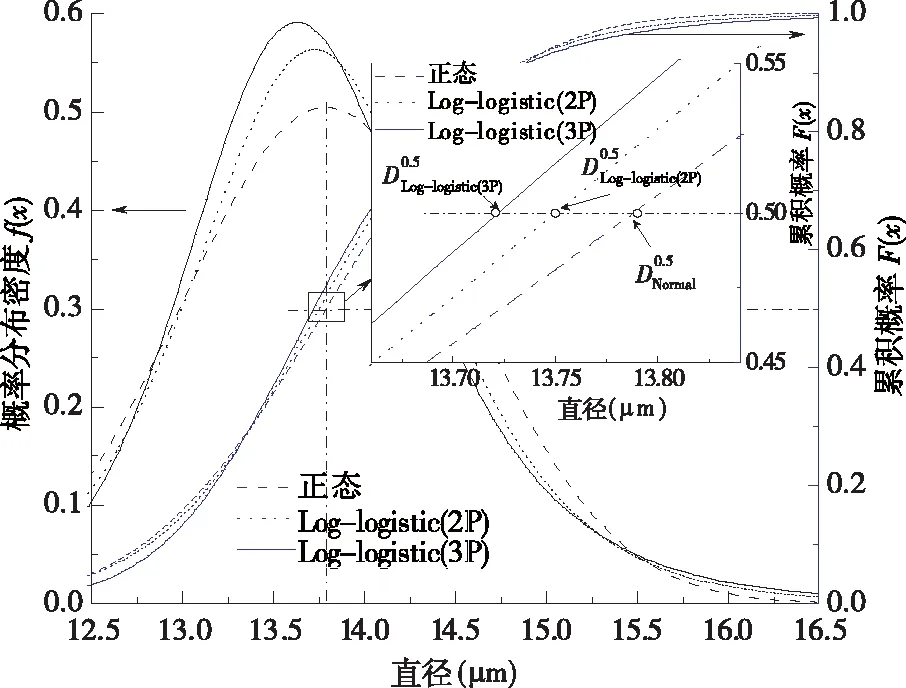
图7 直径计算值对比分析(F(x) =0.5)
这主要是由于正态分布属于无偏分布,而轶纶®短纤维的强力与伸长率呈现右偏分布,导致同等累计概率条件下的计算值大于算术平均值(如图6所示);而对于纤维线密度和纤维直径,其表现为左偏分布特性,从而计算值相对与算术均值像向左偏移,表现为同等累计概率下的计算值小于算术平均值(如图7所示).
3 结 论
本文以轶纶®纤维为研究对象,对其强伸性能、纤维细度进行了测试,并对其性能指标参数的分布进行了分析,并对拟合结果进行检验分析.分析结果表明,纤维性能指标呈现偏态分布特征,对于log-normal分布、Weibull分布以及Log-logistic分布模型,纤维强力及伸长分布采用Weibull(3P)分布模型描述较为合理,纤维线密度及直径采用Log-logistic(3P)分布较为适合.此外,还对分布模型的可靠性进行了分析和讨论,对比分析了同等累积概率下的理论计算值与算数平均值的差异,并从分布模型的形态角度分析了原因.研究还发现,轶纶®纤维的强力和伸长率之间存在弱相关性.
[1] 丁孟贤.聚酰亚胺-化学、结构与性能的关系及材料[M].北京: 科学出版社, 2006:1-5.
[2] Subramanian S,Kannan M,Geethamalini R. Thermally Resistant Fibers[J]. Chemical Fibres International, 2005, 55(2): 32-39.
[3] 尹朝清,徐 园,张清华.聚酰亚胺纤维及其阻燃特性[J].纺织学报,2012,33(6):116-120.
[4] 雷 瑞.高性能聚酰亚胺纤维研究进展[J].合成纤维工业,2014,37(3):53-55.
[5] 陈运能.聚酯复丝中纤维的强伸度及其分布[J].江南大学学报(自然科学版),2002(3):277-280.
[6] 陈国华,丁 辛.短纤维强力的概率分布分析[J].东华大学学报(自然科学版),2004,30(4):46-48,75.
[7] 吴琪琳,潘 鼎.国产粘胶基碳纤维强度的两种统计分布[J].材料导报,2000,14(1):55-56.
[8] Pickering K L,Murray T L.Weak Link Scaling Analysis of High-strength Carbon Fiber[J]. Composites Part A, 1999,30(10):17-21.
[9] 李敏洁,汪泽幸,陈南梁.Vectran 长丝断裂强力的 Weibull分布统计分析[J].丝绸, 2012, 49(10):11-15.
[10] 万传寅,李德清.脆性纤维的强度分布函数-S分布[J].华南理工大学学报(自然科学版),1996,24(7):89-95.
[11] 贾迎宾,杨建忠,李发洲.山羊绒纤维细度变异的研究[J].毛纺科技,2010,38(11):48-50.
[12] 道勒玛,张 强,姚东文,等.阿拉善白绒山羊绒纤维细度分析[J].畜牧与饲料科学,2014,25(11):17-18.
[13] 张一心,李 锦,李 伟.国产羊毛细度分布特征及其对强力测试的影响[J].中国纤检,2005(1):27-29.
[14] 杨 萍, 于伟东.束纤维的拉伸特性与强度——伸长间的关系[J].毛纺科技,2002 (3):20-24.
[15] 何 斌,汪泽幸,刘 清,等.SWNTs/PMIA复合纳米纤维的形态及导电性[J].湖南工程学院学报(自科版),2016,26 (4):55-59.
ProbabilityDistributionofTensilePropertiesandFinenessofYilun®StapleFiberBasedonSkewDistribution
LIU Chao1,WANG Ze-xing1,LI Hong-deng1,PENG Xin-yuan1,LI Wen-hui2
(1. College of Textile and Fashion, Hunan Institute of Engineering, Xiangtan 411104, China;2. HunanYongfei Special Protective Equipments Co., Ltd. Xiangtan 411104, China)
To further study on the physics behavior of Polyimide (PI) fiber, the experiment on tensile behavior and fineness of Yilun®staple fiber are conducted in this study, and the performance indexes are analyzed statistically. The results show that the tensile performance and fineness are characterized by skew distribution. The probability distribution of tensile strength and elongation can be described by three parameters Weibull distribution. Meanwhile, probability distribution of the linear density and diameter can be expressed by three parameters Log-logistic distribution. Meanwhile,it can be found that the relationship between tensile strength and elongation is not significant. On the condition that the cumulative distribution probability is 0.5, the theoretical values of strength and elongation are greater than arithmetic mean, and less than arithmetic mean for linear density and diameter.
polyimide (PI); staple fiber; tensile strength; elongation; linear density; diameter; skew distribution
TS151
A
1671-119X(2017)03-0061-06
2017-03-26
湖南省教育厅青年项目(16B059).
刘 超(1985- ),硕士,讲师,研究方向:非织造材料及产业用纺织品.
汪泽幸(1982-),博士,副教授,研究方向:产业用纺织品.

