一种改进剪枝合并的GM-PHD方法

宋 岩，胡建旺，吉 兵,郭 超

(1.陆军工程大学石家庄校区 信息工程系， 河北 石家庄 050003； 2.中国人民解放军71777部队， 山东 济南 250100)

一种改进剪枝合并的GM-PHD方法

宋 岩1，胡建旺1，吉 兵1,郭 超2

(1.陆军工程大学石家庄校区 信息工程系， 河北 石家庄 050003； 2.中国人民解放军71777部队， 山东 济南 250100)

高斯混合概率假设密度滤波器；多目标跟踪；剪枝合并

0 引言

随着科学技术的发展，多目标跟踪领域受到各国学者的高度重视[1-2]。传统的多目标跟踪均以数据关联为主，该方法在目标数目未知且时变的情况下，跟踪精度会下降[3-4]。近年来，Mahler等人提出了随机有限集(RFS)方法，该方法利用一阶矩的形式，巧妙地避开了数据关联问题，并成功应用到目标跟踪领域，成为研究领域的热点。但是，该方法在进行递推的过程中，存在过多的积分运算，导致工程量巨大，并且难以获得解析解。于是，Vo等人提出了一种新的方法，高斯混合概率假设密度滤波(GM-PHD)[5-6]滤波方法，该方法有效解决概率假设密度递推中多重积分问题，但是随着该算法的递推，高斯分量会无限制增加，这就使计算量变得更加复杂。

1 概率假设密度(PHD)滤波器

在多目标跟踪中，由于随机有限集(Random Finite Set，RFS)[7-8]多目标跟踪不需要数据关联，因此引起国内外学者的高度重视。随机有限集可理解为元素数目随机变化，但变化范围是有限的集合。该方法通过建立集合的形式进行递推，目标状态和量测可分别表示为如下的形式：

Xk={xk,1,xk,2,...,xk,Nk}∈F(χ)，

(1)

Zk={zk,1,zk,2,...,zk,Mk}∈F(ψ)。

(2)

RFS的递推过程中考虑到了目标的新生、衍生、存活和消亡等过程，则k时刻目标状态集可表示为:

Xk=Sk|k-1(x)∪Bk|k-1(x)∪Γk，

(3)

式中，Sk|k-1(x)表示k时刻仍然存活的状态集；Bk|k-1(x)表示k时刻衍生的新的目标状态集；Γk表示k时刻新出现的目标状态集。

k时刻的量测集Zk表示为：

Zk=Kk∪[Θk(x)]，

(4)

式中，Kk表示杂波量的集合；Θk(x)表示观测随机集，文献[9]中给出了详细的说明。

通过上述对目标状态和观测量的RFS建模，推导出多目标贝叶斯的递推式：

预测：

(5)

更新：

(6)

通过随机有限集方法，由近似方法得到k时刻概率假设密度为：

(7)

则可以得到PHD的递推公式(8)为：

Dk|k-1(xk|Z1:k-1)=

(8)

于是更新的概率假设密度(PHD)可表示为：

Dk(xk|Z1:k)=(1-PD)Dk|k-1(xk|Z1:k-1)+

(9)

2 高斯混合概率假设密度(GM-PHD)滤波器

GM-PHD滤波算法[10]之所以能够实现对多目标的递推，这是因为在k-1时刻具有高斯混合形式的多目标PHD递推到k时刻仍然具有高斯混合的形式。

GM-PHD滤波器的实现流程[11-13]：

系统方程为：

xk=f(xk-1)+ωk，

(10)

zk=h(xk)+vk，

(11)

式中，fxk-1为状态转移函数；xk为系统状态量；hxk为系统量测方程；zk为系统量测量；ωk和υk分别表示状态过程噪声和量测噪声，且假定为高斯白噪声，相互之间独立。

GM-PHD滤波器的实现流程主要包括对高斯分量的预测和更新：

① 初始化：初始化可表示为：

(12)

② 预测：新生和衍生目标密度分别表示为：

(13)

(14)

由此可得预测PHD函数为：

Dk|k-1(x)=Ds,k|k-1(x)+Db,k|k-1(x)+γk(x)。

(15)

Ds,k|k-1(x)和Db,k|k-1(x)分别表示存活目标和衍生目标的PHD，即

(16)

(17)

则预测PHD可表示为

(18)

③ 更新：在更新阶段，其PHD可记为：

(19)

3 改进剪枝合并方法

针对GM-PHD算法中，计算量无线增大的情况，提出了改进的剪枝合并方法，来控制GM-PHD的计算量。

GM-PHD算法计算复杂度主要取决于高斯项数目。在k时刻，PHD滤波的计算复杂度为：

(Jk-1(1+JB,k)+Jγ,k)(1+Zk)=Ο(Jk-1Zk)，

(20)

式中，Jk-1为k-1时刻后验PHD的高斯项数目。从式中可知，经过PHD更新后，算法中高斯分量的个数会无限制的增加。针对这个问题，预先设置裁剪门限Tr和合并阈值U，通过这个门限Tr，去除低于该权值的高斯分量，以减少一部分计算量，算法中保留高于该门限Tr的高斯分量；对于分布相近的高斯分量，进行合并处理，以减少计算量，使2个高斯分量合并成一个大权值的高斯分量。

改进的剪枝合并方法在减少高斯分量个数的同时，对合并阈值U提出新的表示方法，使该算法既能减少计算量，又能提高多目标跟踪的精度。

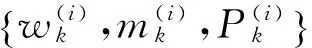
算法流程如下：

PHD函数可以表示为：

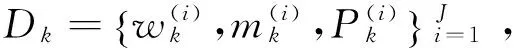
剪枝后的集合表示为集合I：

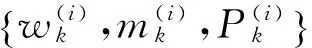
合并过程如下：

(21)

(22)

(23)

该合并距离的优势在于：

③ 引入了u1和u22个系数，充分考虑高斯分量3个重要参数对其合并距离的影响。u1和u2两个系数的具体形式与合并高斯分量的权值有关。通常情况下，可以取：

(24)

(25)

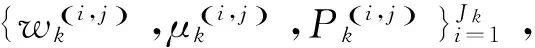
(26)

4 仿真结果与分析

目标的监测区域为[-100 m，100 m]×[-100 m，100 m]。为了简化仿真的条件，实验中仅考虑二维空间中的运动，并且由于衍生目标对目标跟踪的影响较小，故对此不进行严格的考虑说明。假设杂波服从泊松分布：

状态转移矩阵和状态噪声转移矩阵表示如下：

量测矩阵和量测噪声标准差为：

采样时间间隔T=1，杂波平均数为10，存活概率为Ps=0.99，检测概率为PD=0.9，修剪门限Up=10-5，最大高斯数Jmax=100， OPSA的参数定义为c=70、p=2，合并门限Um=5，跟踪时长为50个采样周期。仿真实验如图1所示。

图1 多目标量测值

图1为多目标量测值，从图中可以看出，目标处在大量的杂波环境下，受到各种杂波和虚警等干扰因素的影响，增加了跟踪目标的难度，很难得到需要的有用信息。图2表示目标的真实轨迹与算法状态估计的结果。

图2 多目标真实轨迹及状态估计

图2中，真实目标处在各种干扰因素之下，但在经过改进后的高斯混合概率假设密度滤波器滤波之后，可以得到多目标的状态估计量，并且从图中可以看出，该方法能够较好地跟踪目标，表明算法的可行性。

图3表示对目标数目进行估计，从图中3可以得到不同时刻上多目标数目的估计值。对比于目标数目的真实值，所改进算法能有效估计出监视区域的目标数目，提供目标数目的瞬时信息。由于考虑到了目标的衍生与消亡，在各别孤立点上，会有一定的误差。

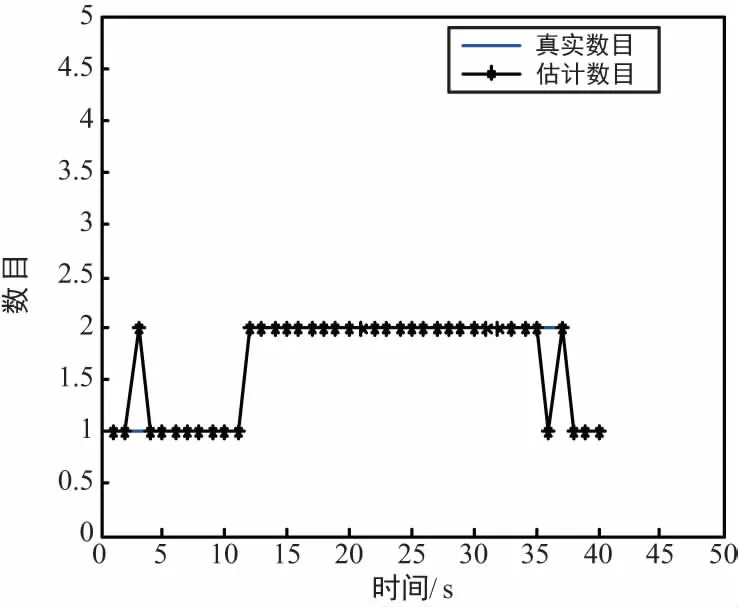
图3 目标数目估计

图4为2种算法经过50次蒙特卡罗实验后的比较情况。最优子模式分配(OSPA)距离是评价多目标状态估计集合和真实集合间估计误差的指标，其值越小表示多目标估计的性能越好，即多目标跟踪的性能越好精度越高。

图4 最优子模式分配距离

从图4中可知，经过改进后的算法进行滤波后，最优子模式分配(Optimal Sub-Pattern Assignment，OSPA)距离小于原始方法滤波后得到的距离，表明改进算法是切实可行的。该改进算法不仅提高了跟踪目标的精度，而且减少了计算量，缩短了算法执行的时间。原算法执行的时间大概为0.54 s，改进算法的运行时间大概为0.47 s，缩短了算法运行的时间，提高了目标跟踪的效率。虽然在有些地方会出现较大的峰值，这是由于新生目标没有及时被检测出来，而消失的目标也未能及时排除。图4中的纵坐标d代表多目标状态估计值和真实值间的估计误差大小，从图中可以看出新改进的算法目标跟踪精度更高。

5 结束语

本文针对GM-PHD算法中，存在计算量大，目标跟踪精度不高等问题，从剪枝合并算法入手提出一种改进方法。该改进方法主要针对剪枝合并过程中，各个高斯分量参数对多目标跟踪的影响，对合并距离d进行了优化。通过大量的仿真实验得出结论：在杂波环境下，该方法有效地减少了计算量并且提高了多目标跟踪的精度。

[1] Syed A P,Hoang D T,Ba N V.Nonlinear Bayesian Filtering Using the Unscented Linear Fractional Transfor Mation Model[J].IEEE Trans Signal Processing,2010,58(2):477-489.

[2] 童慧思,张颢,孟华东,等.PHD滤波器在多目标检测前跟踪中的应用[J].电子学报,2011,39(9):2046-2051.

[3] Wen C L,Li Z L,Xu X B.A New Method for Extracting Fuzzy Evidence from Fuzzy Information Based on Therandom Set Theory[C]∥IEEE,7th World Congress on Intelligent Control and Automation.Chongqing,China,2008:4999-5003.

[4] Mahler R.Statistical Multisource Multitarget Information Fusion[M].Boston: Artech House Publishers,2007.

[5] Kusha P,Daniel C,Ba N V.Data Association Andmanagement for the Gaussian Mixture Probability Hypothesis[J].IEEE Trans Aerospace and Electronic Systems,2009,45(3):1003-1016.

[6] Vo B, Pasha A,Tuan H D.A Gaussian Mixture PHD Filter for Nonlinear Jump Markov Models[C]∥ Proceedings of the 45th IEEE Conference on Decision and Control,California,2006:3162-3167.

[7] Kamaen E W.Multiple Target Tracking Based on Symmetrical Measurement Equations[J].IEEE Transactions on Automatic Control,1992,37(3):371-374.

[8] Mahler R.Multi-target Bayes Filtering Via first-order multi-targetmoments[J].IEEE Transaction on Aerospace and Electronic Systems(S0098-3063),2003,39(2):1152-1178.

[9] MAHLER R．PHD Filters of Higher Order in Target Number[J].IEEE Transactions on Aerospace and Electronic Systems 2007,43(4):1525-1543．

[10] Ba N V,Wing K M.The Gaussian Mixture Probability Hypothesis Density Filter[J].IEEE Trans Signal Pro cessing,2006,54(11):4091-4104.

[11] Ienkaran A,Simon H. Cubature Kalman filters[J]. IEEE Trans Autom Control,2009,54(6):1254-1269.

[12] Vo B N，Ma W K.The Gaussian Mixture Probability Hypothesis Density Filter[J].IEEE Transactions on Signal Processing,2006，54(11):4091-4104.

[13] Luc C，Eric C.Low Costmoving Target Tracking and Fire Control.International Radar Conference on Surveillance for a Safer World[C]∥Bordeaux，France：IEEE,2009:1-4.

AnImprovedAlgorithmofPruningandMergingBasedonGM-PHD

SONG Yan1，HU Jian-wang1，JI Bing1，GUO Chao2

(1. Department of Information Engineering,Army Engineering University Shijiazhuang Campus,Shijiazhuang Hebei 050003,China; 2. Unit 71777,PLA,Ji’nan Shandong 250100,China)

Gaussian mixture probability hypothesis density filter; multi-target tracking; prune and merge

TN713

A

1003-3114(2017)06-45-4

10. 3969/j.issn. 1003-3114. 2017.06.11

宋岩，胡建旺，吉兵，等. 一种改进剪枝合并的GM-PHD方法[J].无线电通信技术,2017,43(6):45-48,85.

[SONG Yan,HU Jianwang,JI Bing,et al. An Improved Algorithm of Pruning and Merging Based on GM-PHD [J]. Radio Communications Technology,2017,43(6):45-48,85.]

2017-06-12

宋 岩(1993—),男,硕士研究生,主要研究方向:指挥信息系统理论及信息融合。胡建旺(1967—),男，教授，主要研究方向:指挥信息系统理论、技术及装备。