地空通信传输中空间调制的适应性分析
李志明,石 荣,肖 悦
(1.电子科技大学 通信抗干扰技术国家级重点实验室,四川 成都 611731; 2.电子信息控制重点实验室,四川 成都610036)
地空通信传输中空间调制的适应性分析
李志明1,2,石 荣2,肖 悦1
(1.电子科技大学 通信抗干扰技术国家级重点实验室,四川 成都 611731; 2.电子信息控制重点实验室,四川 成都610036)
空间调制是一种新型多天线传输技术,在隐蔽通信中具有广阔的应用前景。针对传统空间调制主要集中在地面通信场景下,而极少涉及地空场景应用研究的现状,在对空间调制通信模型简要介绍的基础上,提出了改进的空间调制系统地空通信信道模型,并分别研究了此信道模型中空对地通信传输场景和地对空通信传输场景的信道相关性,以及应用空间调制的适应性。并对上述理论分析的有效性及传输性能进行了仿真验证,从而为空间调制在地空通信中的工程应用提供了重要参考。
MIMO;空间调制;地空通信;相关信道;信道建模
0 引言
地空通信利用无人机、热气球等升空平台搭载通信载荷,相对地面通信传输来讲,具有通信距离远、覆盖面积广、传输带宽大、易于组网和机动灵活等特点,特别适用于空地联合作战中编队迅速推进时的宽带通信联络及城市巷战中的战术通信保障。根据空中平台的升空高度,通信覆盖半径可达几十千米至数百千米[1]。另外,随着航空技术的不断进步,小型飞机也将逐步普及到一般居民的生活中,地空通信在日常生活中的重要性也正日趋明显。
空间调制是一种新型多天线传输技术[2-3]。相较于传统的MIMO系统,空间调制的计算复杂度和天线复杂度低,并且有着更低的峰均比(Peak to Average Ratio,PAPR)及更强的抗相位噪声能力。目前对空间调制的研究大部分集中在地对地通信场景[4-5],文献[6]虽然讨论了空间调制在飞机对地通信中的应用,但信道模型依然建立在低空多径信道的基础上,且没有给出信道相关性与空地距离间的关系。文献[7]针对SISO-OFDM提出了2种空地信道模型:FLYModel-1 和FLY Model-2,并分别针对不同的莱斯因子和信道带宽进行了仿真分析,但没有多天线信道相关性方面的结论。本文针对上述问题,提出了改进的空间调制的空地信道模型,分析了空对地通信和地对空通信场景下的信道相关性,得到了信道相关性与空地距离以及散射体半径之间的关系,并通过仿真验证了上述理论推导的正确性。
1 空间调制通信模型
输入二进制bit数据首先转换为矩阵dL×N,其中L=log2(T)+log2(Mary)为每个时刻发送的bit数,T为天线数,Mary为QAM调制阶数。空间调制的过程就是把矩阵DL×N映射为矩阵XT×N,矩阵XT×N的每列有且仅有一个非零元素,对应的行号为发送天线的索引。如图1所示,假设收发端天线数均为2,输入bit序列为0,1,1T,bit 0表示天线索引1,而后2 bit[11]则用来调制QPSK星座点符号s1,此时天线2不激活,发送符号0。

图1 空间调制原理框图
SM系统的接收符号频域表达式为:
y=HX+N,
(1)
y=HX+N=hls+N,
(2)
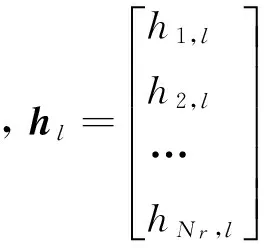
2 地空通信空间调制信道模型
地面与空中平台通信时,在高空的天线周围散射体分布很少[9],几乎可以忽略不计,而在地面的移动终端四周则分布有丰富的散射体。假设散射体分布在以移动用户为中心的圆周上,且信号只经过一次反射到达用户的接收天线。图2为改进的基于单环几何统计信道模型[10-11],地面终端周围不同高度的散射体分布于半径为R的半圆弧上,贴近地表的散射体分布在圆的弦上[12-13]。
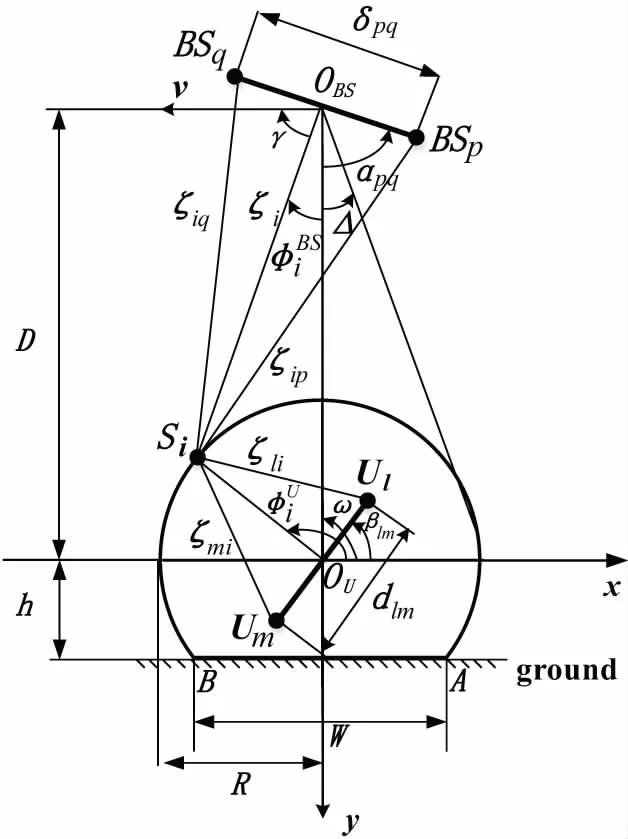
图2 地空通信信道模型
升空台与地面站距离为D,且空地距离D与散射半径R均远大于收发端的天线单元间隔,地面终端发出的信号只在[-Δ,+Δ]范围内可以被高空站接收。
为分析方便,模型中的升空台[14]和地面终端的天线单元个数均为2。若通信双方均采用全向天线,发送天线元BSp到接收天线元Ul之间的信道增益hlp(t)可以表示为直射分量和散射分量的和,即:

(3)
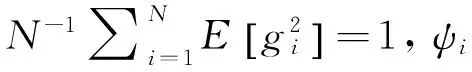
在无线通信系统中,信道的空时相关性对系统性能有着非常重要的影响,下面分析空间调制系统空地信道的空时相关性。信道空时互相关函数可定义为:
(4)
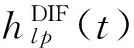

3 信道相关性分析
3.1 空对地信道相关性
升空台的2个天线到地面端的单个天线的信道可以表示为lp、lq,由式(4)可得2个信道间的相关函数为[15]:


(5)

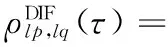
(6)
假设散射体在半圆和弦上均匀分布,借助三角函数公式代入距离参数后得到两信道间散射分量的相关函数为:
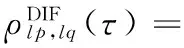
(7)
式中,a为角度AOUy,且:

直射分量的相关函数为:


3.2 地对空信道相关性
地面端的2个天线到升空台的单个天线的信道可以表示为lp、mp,由式(4)可得两信道间的相关函数为:
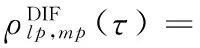


(8)
类似式(6)可将式(8)中散射分量的相关函数变形为:

(9)
假设散射体均匀分布于半圆和弦上,借助三角函数公式代入距离参数后得到两信道间的相关函数为:

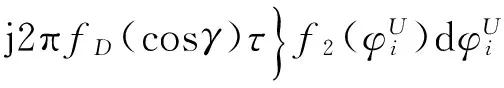

(10)
3.3 信道相关性分析的结论
为了更好地描述前面所推导公式的物理意义,在此通过仿真来对上述信道相关性分析的结论进行展示。考虑地面端离地面高度为1.5 m,升空平台天线单元间距0.2 m,地面终端天线单元间距0.15 m(大于载频单个波长长度),升空平台相对于地面终端仰角90°,莱斯因子为1,通过计算机仿真得到空对地信道的相关性曲线,如图3所示。
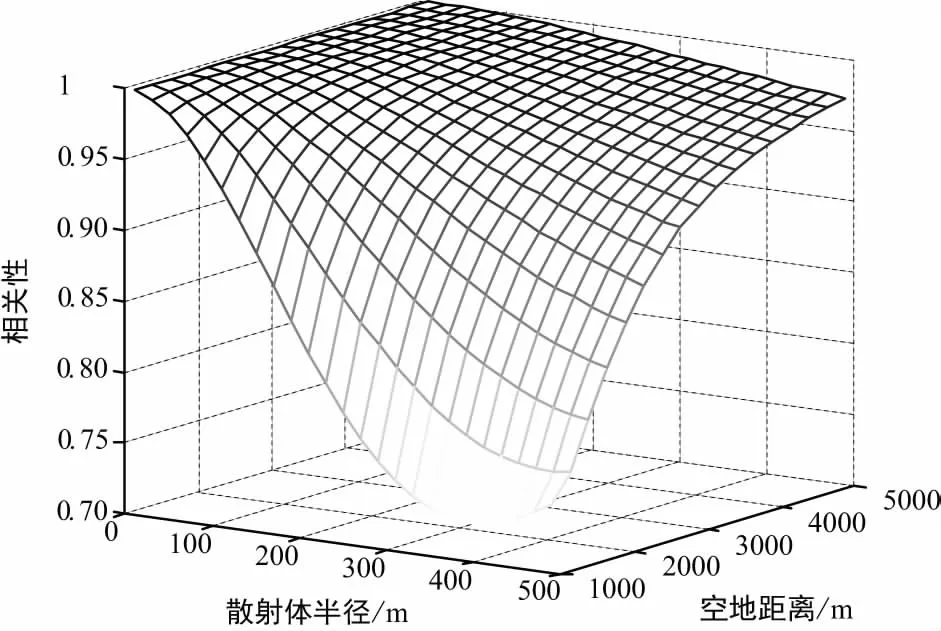
图3 空对地信道相关性与散射体半径和空地距离之间的关系
由图3可见,从空中向地面传输信息时,信道间的相关性很强,在空地距离大于4 km时,信道相关系数几乎接近于1,此时若使用空间调制,地面端将很难通过信道的差别分辨出发送天线的索引位置;而在空地距离小于2 km时,随着散射体半径的增大,信道相关性逐渐降低,最终能过渡到适宜空间调制传输的相关性范围。
从式(8)可以看出,地对空信道的接收相关性与空地距离D没有关系。通过计算机仿真得到地对空信道的相关性与散射体半径之间的关系如图4所示。
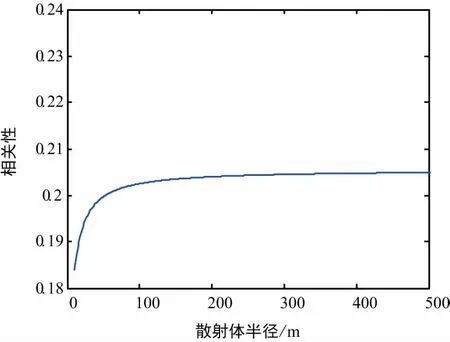
图4 地面终端对升空台传输信道的相关性与散射体半径的关系
由图4可见,从地面向空中传输信息时,信道间的相关性比较弱。随着散射半径的增加,地面终端天线单元间距离与散射半径比值变小,相关性呈略微上升趋势。在散射体半径大于200 m时,信道相关系数小于0.21,此时若使用空间调制,升空台可以比较容易分辨出发送天线的索引位置。
从上述空对地信道和地对空信道的相关性分析结果可以得到如下结论:在地对空传输中适于采用空间调制,而在空对地传输中不适于采用空间调制。
4 仿真验证
在仿真过程中,考虑地面移动通信与地空通信的融合,且地面终端与升空平台的相对运动速度小于200 km/h,所以仿真所用的OFDM系统采用了类似LTE系统中带宽为10 MHz时的参数设置[16-17]:IFFT长度为1 024,循环前缀cp长度为128个采样点,采用QPSK调制方式,收发天线数均为2。作为仿真对比的独立信道为EVA信道,各天线间不相关。在空对地通信和地对空场景下,不同的散射体半径和空地距离得到的BER曲线如图5和图6所示。
从图5可以看出,在空对地传输时,空地距离与散射体半径对空间调制的BER性能影响都很大。当空地距离为1 km时,散射体半径由100 m增加到400 m,空间调制的性能有了较明显的改善,说明散射体半径与BER值呈负相关。当固定散射体半径为400 m,空地距离从5~3 km,再降低到1 km,最后到600 m,BER性能逐渐提高,即空地距离与BER值呈正相关。而当空地距离大于5 km后,即使在散射半径为400 m时,BER曲线依然没有下降的趋势。
从空间调制空对地传输场景的BER仿真性能可以看出,随着空地距离的减小或者散射体半径的增大,信道的相关性都有减弱的趋势,这与本文前一节中空对地信道的接收相关性结论相同。但在空地距离大于1 km时,空间调制的性能与独立信道的对照曲线的差距还是很大的,而当空地距离小于1 km时,升空平台周围的散射体逐渐增多,空地通信退化为地面通信。所以,在空对地传输信息的场景下,空地距离大于1 km后,空间调制的应用有很大的障碍。
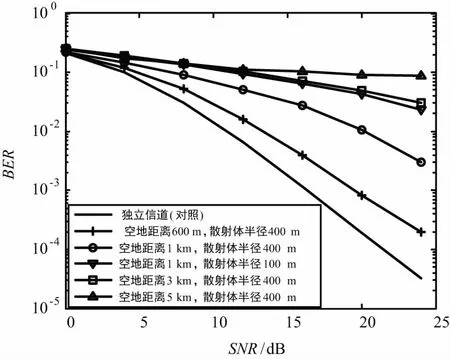
图5 空间调制空对地场景不同参数下的仿真比较
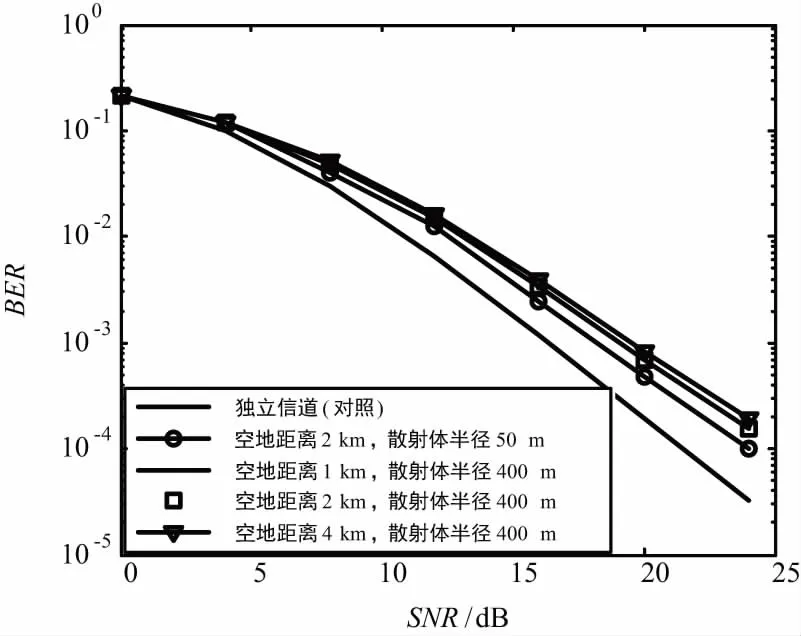
图6 空间调制地对空场景不同参数下的仿真比较
由图6可见,在地对空通信场景下,当散射体半径固定为400 m时,空地距离2 km和4 km的2条BER曲线相差很小,空地距离2 km和1 km的曲线几乎重合,说明不同的空地距离对空间调制的BER性能影响不大。固定空地距离为2 km,随着散射体半径从400 m减小到50 m时,BER性能有些许改善,在BER为10-3时性能提升了大约1 dB。从整体上看,空间调制在地对空传输信道下的BER曲线在10-3时,仅比对照曲线差2 dB左右,说明空间调制能够在地对空通信场景下正常发挥性能。
空间调制在地对空传输场景下的BER性能随空地距离的减小而有小幅的提高,与本文前一节中地对空传输信道的接收相关性结论相符。而地对空信道下的BER性能随空地距离增大而略微降低,所以可得出如下结论:相比于常规的瑞利信道环境,空间调制能够在损失些许性能的情况下应用于地对空通信传输中。
5 结束语
针对空间调制在地空通信场景下研究的缺失,首先构建了空间调制地空通信模型,对基于单环几何统计信道模型进行了改进,并根据改进的信道模型推导了地对空通信和空对地通信场景下的接收相关性。通过对两个场景下空间调制的BER进行计算机仿真,BER曲线变化趋势与相关性结论吻合,从而得到如下结论:空间调制能够应用于地对空通信传输中,而在空对地通信场景下,空间调制只能在一定的空地距离下发挥作用,从而为空间调制在未来无人机等飞行器的空地通信系统研制中的应用提供了理论基础与参考依据。
[1] 高自新,徐文娟.地空信道传输特性与技术分析[J].无线电工程,2012,42(2) :10-12.
[2] MeslehR Y,Haas H,Ahn C W,et al.Spatial Modulation- A New Low Complexity Spectral Efciency Enhancing Technique[C]∥in Proc.IEEE Int.Conf.Commun.Netw.China,Beijing,China,2006:1-5.
[3] MeslehR Y,Haas H,Sinanovic S,Ahn C W,et al.Spatial Modulation[J].IEEE Trans.Veh.Technol.,2008,57(4):2228-2241.
[4] RenzoM D,Haas H,Grant P M.Spatial Modulation for Multiple-antenna Wireless Systems:A survey[J].IEEE Commun.Mag.,2011,49(12):182-191.
[5] Yang P,Xiao Y,Guan Y L,et al.Single-carrier SM-MIMO:A Promising Design for Broadband Large-scale Antenna Systems[J].IEEE Communications Surveys & Tutorials,2016,18(3):1687-1716.
[6] Raddadi B,Thomas N,Poulliat C,et al.On the Use of Spatial Modulation in Aeronautical Communications[C]∥Wireless and Mobile Computing,Networking and Communications (WiMob),2016 IEEE 12th International Conference on.IEEE,2016:1-8.
[7] Jun M,Chunsheng Z,Liang T,et al.AeronauticalChannel Modeling and Simulation[C]∥Control Conference (CCC),2012 31st Chinese.IEEE,2012:5577-5581.
[8] Rappaort T S.Wireless Communication Principles and Practice[M].北京:电子工业出版社,1999.
[9] 习靖,习强,郑淑梅.地空信道二径模型及仿真[J].无线电工程,2007,37(7) :58-60.
[10] Abdi A,Kaveh M.A Space-time Correlation Model for Multielement Antenna Systems in Mobile Fading Channels[J].IEEE Journal on Selected Areas in communications,2002,20(3):550-560.
[11] Samad A M,Kamarulzaman N,Hamdani M A,et al.The Potential of Unmanned Aerial Vehicle (uav) for Civilian and Mapping Application[C]∥in System Engineering and Technology (ICSET),2013 IEEE 3rd International Conference on,Aug 2013:313-318.
[12] 杨大成.移动传播环境[M].北京:机械工业出版社,2003.
[13] Perahia E,Cox D C,Ho S.Shadow Fading Cross Correlation Between Basestations[C]∥Vehicular Technology Conference,2001.VTC 2001 Spring.IEEE VTS 53rd.IEEE,2001,1:313-317.
[14] Blandino S,Kaltenberger F,Feilen M.Wireless Channel Simulator Testbed for Airborne Receivers[C]∥Globecom Workshops (GC Wkshps),IEEE,2015:1-6.
[15] 李忻,聂在平.MIMO 信道中衰落信号的空域相关性评估[J].电子学报,2004,32(12):1949-1953.
[16] 韩宜君.高速移动场景下基于TD-LTE标准的信道估计技术[D].北京:北京交通大学,2014.
[17] 朱秋明.非均匀散射空时频相关MIMO信道建模与仿真研究[D].南京:南京航空航天大学,2012.
AdaptabilityAnalysisofSpatialModulationinAir-groundCommunications
LI Zhi-ming1,2,SHI Rong2,XIAO Yue1
(1.National Key Laboratory of Science and Technology on Communications,UESTC,Chengdu Sichuan 611731,China; 2.Science and Technology on Electronic Information Control Laboratory,Chengdu Sichuan 610036,China)
Spatial modulation is a new multi-antenna transmission technology,which has a great promise for covert communication.Conventional studies on spatial modulation mainly concentrate on ground communication scene,while the application in air-ground scene is rarely discussed.Considering the above fact,an improved air-ground communication channel model of spatial modulation is constructed on the base of a simple spatial modulation channel model.Furthermore,the channel correlations of air-to-ground and ground-to-air scenes are also discussed.Besides,the practicability of applying spatial modulation in air-ground communication is also analyzed.With respect to the above theoretical analysis,the effectiveness and transmission performance of spatial modulation are validated through simulation,which gives an important reference to the application of spatial modulation in air-ground communication.
MIMO;spatial modulation;air-ground communications;correlated channel;channel modeling
TN92
A
1003-3114(2017)06-31-6
10.3969/j.issn.1003-3114.2017.06.08
李志明,石荣,肖悦.地空通信传输中空间调制的适应性分析[J].无线电通信技术,2017,43(6):31-36.
[LI Zhiming,SHI Rong,XIAO Yue.Adaptability Analysis of Spatial Modulation in Air-ground Communications[J].Radio Communications Technology,2017,43(6):31-36.]
2017-07-25
国防科技重点实验室基金项目(JS17041403811)
李志明(1993―),男,硕士研究生,主要研究方向:无线与移动通信。石 荣(1974—),男,博士,研究员,主要研究方向:电子对抗、通信与雷达系统。

