基于二分法的K-means算法的实现

陈贤宇，李有强，吕苗苗，卢建成，陈文强

(安徽大学 计算机科学与技术学院，安徽 合肥 230039)

基于二分法的K-means算法的实现

陈贤宇，李有强，吕苗苗，卢建成，陈文强

(安徽大学 计算机科学与技术学院，安徽 合肥 230039)

在图像处理大领域内，对特征值的处理尤为重要，而K-means算法是被运用于特征值聚类的重要方法之一，该方法简单快捷，聚类效果较佳，因而被学术界广泛使用。针对传统的K-means算法在进行数据集划分过程中的不足之处，提出了一种基于二分法的K-means聚类算法，该算法对数据集进行划分来选择出下次划分的数据集，以此来形成迭代，实验表明该算法相比于传统算法在划分方面有了明显的改进。

K均值；二分法；聚类中心

0 引言

在数据处理与查询领域，专家学者们提出过很多种有效的方法，其中传统的K-means方法是早期一个基于中心的经典的聚类方法，因其理论研究可靠，算法简单，时间复杂度低而被广泛应用。当然，传统k-means在数据处理方面存在一定缺陷[1-3]：传统的K-means聚类算法对聚类中心的选取有一定的局限性，其过分依赖于聚类中心的选取；实验之前，往往无法确定聚类参数K的取何值时可使得聚类效果更好。所以在实际应用中，就很难获得一个适当的K值来使聚类效果更佳，这样便增加了用户的负担。由上可知传统k-means的这些缺陷使得学者对聚类算法的研究仍在继续，试图找出一种可以代替或者改进传统K-means算法的优质聚类算法。

考虑到传统K-means算法在某些方面的局限性，学者们做过一系列的研究，例如，在离散数据的快速聚类方面，有学者提出k-modes算法，这种算法在保留K-means算法效率的同时又实现了对离散数据的处理，使得实验的应用范围有所扩大。其次，在K-modes算法方面有所延伸的k-Prototype算法，该算法不仅考虑到了离散数据的特殊情况，还考虑到了数据集的数据属性，将这2种情况加以融合即得到k-Prototype算法，该算法提出了相异性度量标准的概念，使实验效果有所提高。

本文从整体数据集出发，试图找出二分后的数据对K-means聚类的帮助作用，这样就可以克服K均值算法收敛于局部的问题，可以使得实验效果更佳。

1 传统K-means算法

1.1 具体步骤

从文献[4-6]中可以归纳出传统的K-means算法步骤。输入：聚类数值K和含有N个对象的数据集X=x1,x2,x3,...xn。输出：K个聚类簇s1,s2,s3...sk实验效果是使目标函数最小。

①从 数据集X中随机选择K个对象作为初始聚类中心c1,c2,c3,...ck；

② 重复；

③ 逐个将对象xii=1,2,3...n按照欧式距离分配给最近的一个聚类中心cj，1≤j≤k1≤j≤K,则：

(m为数据属性的个数)；

④ 重新计算每个簇中新的聚类中心cj,cj=1/Nj∑xi,j=1,2,3...kj,Nj是第j个 簇sj中对象的个数；

⑤ 直到K个聚类中心不在变化，准则函数收敛。

传统K-means算法的基本流程图如图1所示。

图1 传统K-means算法流程图

据此专家学者们通过大量实验验证该算法的可行性，同时可以看到K-means算法浅显易懂，可以通过图2了解K-means算法的核心思想:从数据集中随机选择K个对象作为初始聚类中心，然后计算数据集中每个对象与这些中心对像的距离，距离符合条件的划分一类，不断调整检测标准重复上述步骤即可完成实验。

图2 K-means算法图示

1.2 传统K-means算法的优缺点

K-Means聚类算法的优点简单来说有以下几点[7-9]:① 算法快速、简单；② 该算法对大数据集有较高的效率；③ 时间复杂度近于线性，而且适合挖掘大规模数据集。K-means聚类算法的时间复杂度是on*k*m,其中n为数据中数据对象的个数，m为算法迭代的次数，k为认为设定的聚类初值。

相比较而言，传统K-means算法有以下几个主要的不足之处:① 在 K-means 算法中K是事先给定的，这个K值的选定是非常难以估计的，因而事先不知道该选取何值来进行聚类；② 该算法在每一次迭代过程中都会产生新的聚类中心，因而数据量比较大，导致算法的时间开销加大；③ 该算法对数据集中的噪声点和孤立点比较敏感，这将会导致均值偏离严重；④ 初始聚类中心对后期的实验影响比较大，一旦初始值选择的不好，可能无法得到有效的聚类结果等等。

2 改进算法的研究与实现

2.1 改进算法的引入

在基础阶段本研究小组通过阅读大量文献资料，梳理了传统K-means算法的核心思想以及实现步骤，通过实验可以获得较好的聚类效果图。基于创新的概念，思考了几种可能的改进措施：在图像特征值聚类方面，思考能否通过一幅图像的局部内在联系进行聚类[10]，以人脸为例，每个人都有一张互不相同的脸，但是人脸上的基本构造却是相同的，嘴巴都是位于鼻子下面，而鼻子位于眼睛下面等等，诸如此类图像内在联系可以找出很多。在不存在内在联系的数据集中，又该怎样改进算法以获得更好的效果呢？结合数学中的相关知识，提出基于二分法的K-means算法，类似求方程的解，在求解中通过对固定区间进行二分法来逼近零点可以求得方程的解，运用到聚类中，如何定义区间和零点显得格外重要，通过分析发现，对于二分区间可以直接取自数据集，将整个数据集当作区间来进行划分符合要求，其次将K值类比为零点，通过无限划分将数据集的个数无限逼近K值即可完成聚集。

在对基于图像局部联系的聚类算法的实现过程中，发现其中困难多多，对于不同的图像，必须首先定义不同的局部联系关系，而自然界中的图像无穷无尽，对每一类图像都定义局部联系会使工作量成倍增加，有时又因为图像保存时间、像素以及图像内容的复杂性等原因使得实验极其复杂，实验效果较差，甚至无法得出实验结果。为此，改用二分法对数据集进行聚类研究，二分法实验原理简单易行，又涉及传统K-means算法的使用，故比较容易实现，所以通过对实验的基本思想、实验内容、实验步骤以及实验效果进行的系统的设计与操作，提出基于二分法的K-means聚类算法。

2.2 改进算法的基本思想与主要步骤

对于一个原始的数据集，把它看成一个整体，类比与二分法求解中的区间整体，这里将这个整体命名为簇(cluster)，然后将该簇利用K-means算法一分为二即得2个数据集(簇)，然后选择其中一个簇进行再次二分划分，以此类推，从而形成迭代，直至数据集的数目等于用户指定的数目K为止。

在实验思想的指导下，结合传统K-means算法提出本次实验的基本步骤如下：① 把所有的数据集初始化为一个簇；② 对第1步中得到的簇执行K-means算法划分为2个簇(初始化时只有一个簇)，然后一直重复第2步的划分(选某个簇进划分为2个)，直到得到K个簇为止。

2.3 改进算法的实现

这里观察到选择不同的数据集进行下次聚类所得到的效果是不同的，那么如何进行数据集的选择呢？起初考虑总是向同一个方向进行数据集的选择，简单的说就是总是选择上半方的数据集或者下半方的数据集，通过对这个方案的实验，发现聚类效果不佳，无法考虑到至关重要的特征向量，聚类效果存在极端现象。紧接着转换思想，跳跃选取下一次要聚类的数据集，也即每进行一次聚类就转换一次选取方向，这样可以中和实验效果，此方法相对于前一种方法有了明显的改进，消除了部分的极端现象。

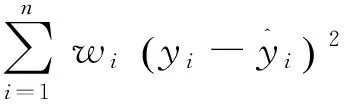
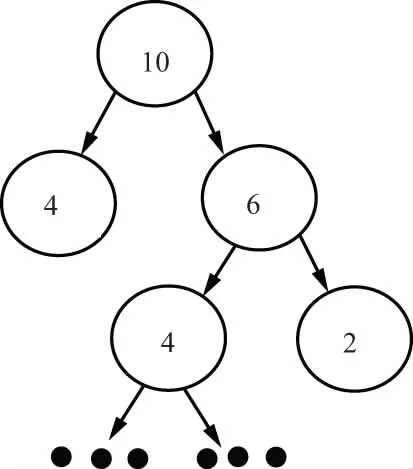
图3 改进算法的示意图

由图3所示，假设初始数据集含有10个特征向量，在第一次选择之后得到2个分别为4和6个特征向量的聚类簇，这时执行二分选择算法，选择具有6个特征向量的聚类簇行下次划分，因为数据集所含特征向量越多就表明该簇聚类越不好，这时就应该选择该聚类簇进行下一次聚类，以此类推。改进算法的流程图如图4所示。

由图4可知，改进算法在传统K-means算法的基础上添加了二分选择这一实验步骤，其目的是为了选出适合后期进行二次聚类的聚类簇。

图4 改进算法的流程图

改进算法的效果图如图5所示。

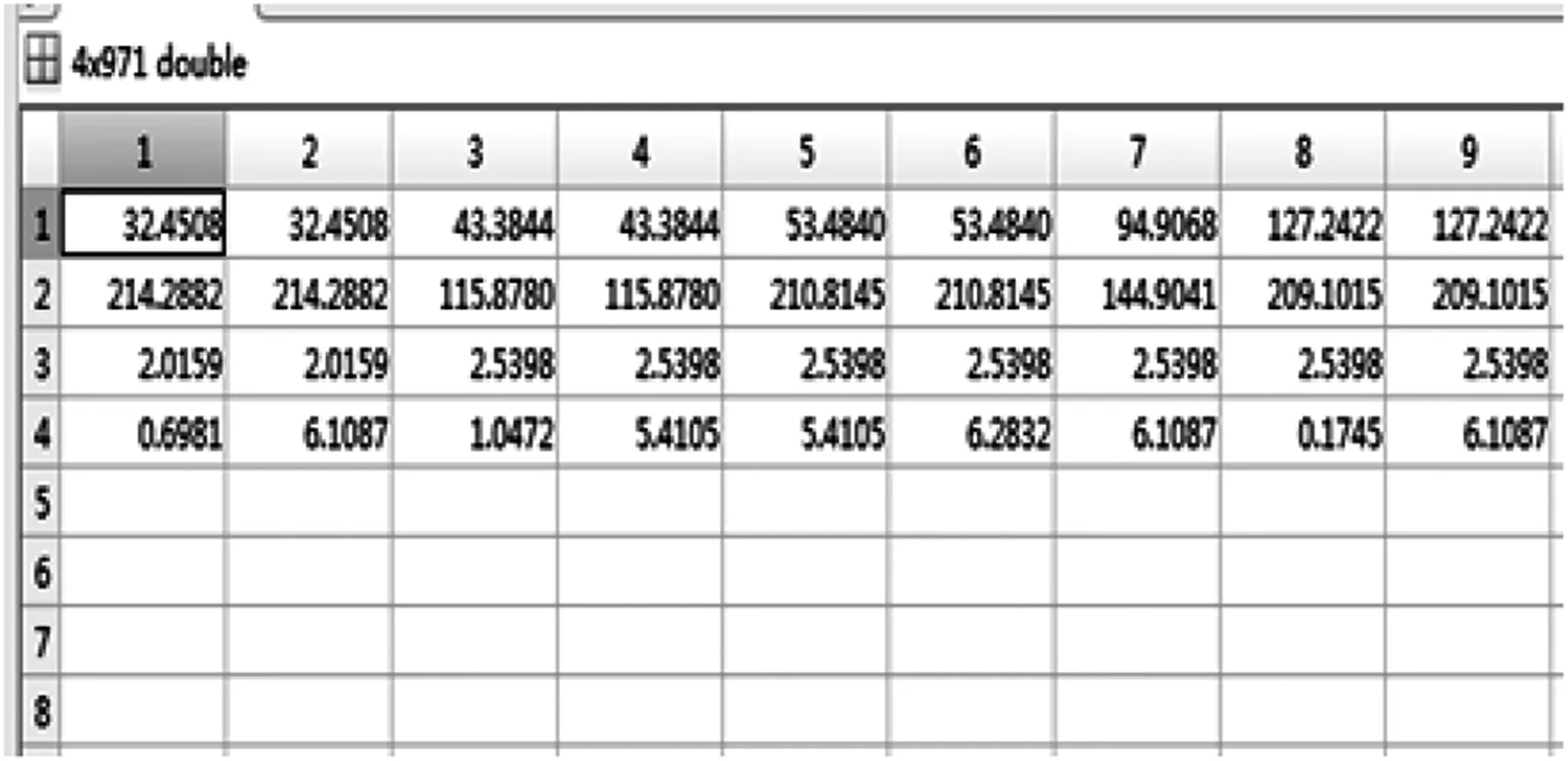
(a) K=4时聚类的特征值向量矩阵

(b) 特征值匹配效果图 图5 改进算法的效果图

2.4 改进算法与原始算法的比较

在传统K-means算法中，用户需要自行选取聚类中心，这无疑给实验增加了不确定性，也使得实验结果无法快速达到最好的聚类效果，而改进的基于二分法的K-means算法中，不存在随机点的选取，不受初始化问题的影响，故误差较小，实验效果较好。其次，二分K-means算法的时间复杂度有所减小，因为该算法相比于传统K均值算法而言，它减少了特征值的相似度计算等等。

3 结束语

传统的K-means算法是一种在数据集聚类方面应用比较广泛的聚类算法，但它存在一定的局限性和不确定性。本文提出的基于二分法的K-means聚类算法是对传统算法的改进，有效性分析和实验表明，基于二分法的K-means聚类算法较大的提高聚类性能，但仍存在着局部聚类效果不佳的问题，故仍需进一步研究。

[1] Papadopoulos G T,Mezaris V,Kompatsiaris I,et al. Probabilistic Combination of Spatial Context with Visual and Co-occurrence Information for Semantic Image Analysis[C]∥ Proc.IEEE International Conference on Image Processing (ICIP 2010),Hong Kong,China,2010:3205-3208.

[2] Escalante H J,Montes-y-Gómez M，Sucar L E.An Energy-based Model for Region-labeling[J].Computer Vision and Image Understanding，2011，115(6)：787-803.

[3] Fergus R,Perona P,Zisserman A. Object Class Recognition by Unsupervised Scale-invariant Learning[J].Cvpr,2003,2(2):264.

[4] 张建民.一种改进的K-means聚类算法[J].微计算机信息，2010(9):233-234.

[5] 朱玉金，孙蕾.数据挖掘技术[M].南京：东南大学出版社,2006.

[6] 张云涛,龚玲.数据挖掘原理与技术[M].北京:电子工业出版社,2004.

[7] 李芳.K-Means算法的k值自适应优化方法研究[D].合肥:安徽大学,2015.

[8] 李荟娆.K-means聚类方法的改进及其应用[D].哈尔滨：东北农业大学,2014.

[9] 崔卫东.K-means算法研究[J].数字化用户,2013,19(11):35-40.

[10] 李正兵,罗斌,翟素兰,等.基于关联图划分的K-means算法[J].计算机工程与应用,2013,(21):141-144，151.

[11] Michael S,George K,Vipin K.A Comparison of Document Clustering Techniques[J].International Transactions in Operational Research,2017，24(3):537-558.

[12] 陈姗姗.基于Hadoop的用户行为分析方法的应用研究[D].南京：南京邮电大学,2016.

ImplementationofK-meansAlgorithmBasedonDichotomy

CHEN Xian-yu,LI You-qiang,LU Miao-miao,LU Jian-cheng,CHEN Wen-qiang

(School of Computer Science and Technology,Anhui University,Hefei Anhui 230039,China)

The eigenvalue processing is very important in the field of image processing. The K-means algorithm is one of the most important methods used in eigenvalue clustering. This algorithm is simple and quick,and the clustering effect is better,so it is widely used by academic community. In view of the deficiencies of conventional K-means algorithms in data set partition,this paper puts forward a K-means clustering algorithm based on the dichotomy. By partitioning the data set,this algorithm selects the data set to be partitioned for iterations. The experimental results show that the proposed algorithm has significantly improved in terms of partitioning compared with conventional algorithms.

K-means; dichotomy; clustering center

TP391

A

1003-3114(2017)06-37-4

10. 3969/j.issn. 1003-3114. 2017.06.09

陈贤宇，李有强，吕苗苗，等. 基于二分法的K-means算法的实现[J].无线电通信技术,2017,43(6): 37-40.

[CHEN Xianyu,LI Youqiang,LU Miaomiao,et al. Implementation of K-means Algorithm Based on Dichotomy [J]. Radio Communications Technology,2017,43(6): 37-40.]

2017-05-25

安徽大学创新创业项目(J10118515835)

陈贤宇(1996—),男,本科,主要研究方向：模式识别。李友强(1997—),男,本科，主要研究方向：图像检索。