基于非对称交互多模型算法的上升段弹道估计

耿林玉,吴 楠,孟凡坤,韩佳颖

(1.解放军信息工程大学,河南 郑州 450001;2.96669部队,北京 102208)

基于非对称交互多模型算法的上升段弹道估计

耿林玉1，2,吴 楠1,孟凡坤1,韩佳颖2

(1.解放军信息工程大学,河南 郑州 450001;2.96669部队,北京 102208)

弹道导弹上升段涵盖助推段和自由段,动力特征复杂,传统跟踪算法难以获得其全程稳定高精度的弹道估计。对此提出一种用于上升段弹道估计的自适应非对称交互多模型算法,模型集由三维当前统计模型和精确动力学模型构建,并对模型状态矢量进行统一。仿真结果表明,算法实现了对导弹上升段稳定高精度跟踪以及关机点的有效检测,与传统CS算法相比较,自由段弹道估计精度提高68.9%,且可有效检测导弹的运动模式切换,检测延迟小于2s,滑行段暂态误差降低79.5%。

机动弹道估计; 非对称交互多模型; 机动检测; 稳定跟踪

吴 楠(1984-),男,博士,讲师。

孟凡坤(1963-),男,硕士,教授。

韩佳颖(1985-),女,硕士,工程师。

随着探测技术的最新发展,各国导弹防御体系纷纷谋求上升段预警拦截,与此同时,导弹上升段复杂的运动特性给导弹防御体系的探测、跟踪、落点预报带来了新的挑战[1-4],因此开展上升段弹道估计算法的研究,对于重构导弹防御体系极为迫切。

机动弹道估计算法也称机动目标跟踪算法,目前主要分为两类:单模型算法和多模型算法[5-6](Multiple Model,MM)。弹道上升段既包含助推段,又包含一部分自由段,通过仿真[4]可知,基于单模型算法的机动弹道估计无法兼顾机动段与非机动段的估计精度,因此单模型算法不适用于上升段的弹道估计。

目前针对导弹上升段的弹道估计研究较少,探索新的多模型算法必将是主流趋势。多模型算法的总体思想是将机动目标跟踪描述为一个混合估计问题,其最大的特点就是引入了模型概率的概念:多个子模型滤波器并行工作,当目标运动模式改变时,通过模型概率的变化实现模型权重的转换,以多个模型的加权和作为目标的状态估计。

多模型算法的发展经历了三个阶段[7]:静态多模型,交互多模型(Interacting Multiple Model,IMM)和变结构交互多模型。其中以基于IMM估计的应用最为广泛,该算法在多模型的基础上,假设不同模型之间的转移服从已知转移概率的有限态马尔可夫链,考虑多个模型间的交互作用,从而得出目标的状态估计。IMM实现了自适应跟踪的同时兼顾了估计性能与计算效率[8-10],被认为是最有效的混合估计方案。

本文针对弹道导弹上升段的复杂机动特性,基于IMM提出一种自适应非对称IMM弹道估计算法,使用精确动力学模型和三维当前统计模型[6](Current Statistical Model,CS)构成运动模型集,并对两者的状态矢量和协方差矩阵进行维数统一。通过两个子滤波器状态估计的组合得到整体的状态估计,以此减小估计过程中因模型不确定性造成的估计误差。

仿真表明,与基于单个CS算法的上升段弹道估计相比,自适应非对称IMM算法不仅实现了助推段的稳定跟踪,减小了自由段的估计误差,同时实现了模型的自由切换,对导弹滑行段进行了有效检测,降低了滑行段暂态误差,提高了关机点的估计精度。

1 非对称交互多模型算法

1.1 模型集构建

弹道上升段既包含助推段,又包含一部分自由段。其中助推段内导弹受发动机推力、二体引力和非球体摄动力作用,机动特性明显;自由段内导弹仅受地球的二体引力和非球体摄动力作用,保持自由飞行状态,运动规律性强。

针对上升段的特性,本文选择多模型算法进行弹道估计,助推段采用三维CS,自由段采用基于J2摄动的精确动力学模型,二者共同构成IMM的模型集。这两个模型经常应用于弹道估算,但因其目标状态矢量和协方差矩阵维数不同,鲜有文献将其二者构成模型集,因此本文着重讲解如何进行维数统一,两个子模型的构建算法不再赘述。

1.2 维数统一

本算法关键是要解决非对称问题:IMM最终输出的目标状态矢量为九维,其中基于三维CS弹道估计的状态矢量为九维,其协方差矩阵为9阶;但基于精确动力学模型弹道估计的状态矢量为六维,其协方差矩阵为6阶。因此,为实现状态估计的交互,需将两个子模型滤波输出的目标状态矢量和协方差矩阵在交互前进行维数统一。

思路有两种:1)对基于三维CS估计的状态矢量和协方差矩阵进行降维;2)对基于精确动力学模型估计的状态矢量和协方差矩阵进行维数扩展。 考虑到后续需从交互后的目标状态矢量和协方差矩阵中提取子模型输入,第一种方法需要经过两次复杂的维数变换,计算量过大。本文选择对基于精确动力学模型的弹道估计进行维数扩展,以统一非对称模型的维数。对基于精确动力学模型的机动弹道估计算法增加变维方程:

X2(k)=g(k,X1(k))

(1)

对导弹在精确动力学模型中的目标状态方程进行推导得向量g:

(2)

其中:

(3)

计算向量g的雅各比矩阵k时刻在最近的状态估计取值gx(k),用gx(k)对P1(k)进行扩展得到九维的协方差矩阵:

(4)

由此精确动力学模型的维数得到扩展,此时交互多模型具有九维目标状态矢量,所得估计结果中包含加速度估计值。

需要注意的是,在进行EKF滤波时,精确动力学模型的目标状态矢量需取交互后目标状态矢量的前六维,协方差矩阵需取交互后状态矢量协方差矩阵的前6×6部分。

1.3 滤波初始化

采用三维CS与精确动力学模型作为子模型构成多模型算法的模型集后,本文采用扩展卡尔曼滤波[8](Extended Kalman Filtering,EKF),分别对两者进行滤波,继而对所得状态估计进行交互。

考虑EKF与三维CS滤波初始化时采用的观测数据点数不同,为实现子模型的并行工作,对模型的滤波初始化做出一些改变。

从k=4时刻统一开始进行两个模型的计算和交互,用两模型交互后的所得值作为滤波的初始化输入数据。

1.4 算法流程

经典IMM算法是在多模型算法的基础上增加马尔科夫转移,考虑多个模型的交互作用根据似然函数,计算每一个模型的正确概率,以多个模型的加权和作为目标的状态估计。

本文算法在经典IMM的基础上,解决了子模型间维数不同的问题,即在对子模型的估计结果进行交互前,对模型维数进行了统一,总体思想如图1所示。

图1 自适应非对称交互多模型算法示意图

算法从k时刻到k+1时刻递推过程如下:

1)状态交互

(5)

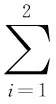
(6)

其中,

(7)

2)模型条件滤波

3)模型可能性计算

若模型i滤波残差为vi(k+1),相应协方差为Si(k+1),并假定服从高斯分布,使用Λ(k)表示模型可能性向量,则模型i的概率为

(8)

其中,

(9)

4)模型输出

(10)

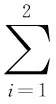
(11)

由算法流程可知,IMM有独特的优势——依据模型概率可以判断目标的运动状态。分析可知,非机动状态下基于精确动力学模型的弹道估计结果精确性更高,因此其概率应明显大于基于三维CS的机动弹道估计;同理,当目标机动时后者的模型概率显著增加并超过前者。

2 仿真与结果分析

2.1 参数设置

为验证算法有效性,利用一条已知弹道数据的7000km射程弹道导弹弹道进行仿真。根据采样点,用样条拟合法估计出采样值之间的航迹,得到地固系中上升段三维弹道曲线如图2,求速度对时间的导数得x,y,z三轴方向上的加速度——时间曲线如图2。

根据弹道轨迹,将地基雷达设置在L=5°,B=3°,H=0,观测数据的标准差分别为σR=100m,σA=0.01deg,σE=0.01deg,观测间隔T=0.1s。根据地基雷达与弹道的几何关系及雷达探测模型获得雷达观测数据的真值如图3、4所示。

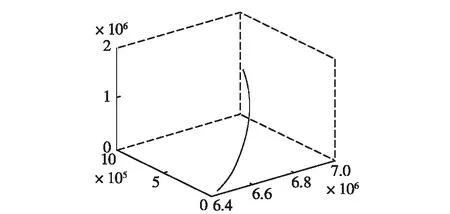
图2 导弹上升段三维弹道曲线

由图3可知,导弹在X轴方向平均加速度最小,机动性较弱,在Z轴方向上最大加速度达到96m/s2,机动性最强。

由图4可知,该雷达可完整跟踪上升段弹道,探测过程中,斜距先变小再变大,同时俯仰角先变大再变小,说明弹头相对于雷达先接近再远离,两者斜距最小为295.1km,最大为3320.8km。

图3 上升段axayaz随时间变化的曲线

图4 雷达观测数据真值

为方便计算,截取100s～400s上升段数据进行仿真。在这300s内,124s时二级发动机关机,经历2s滑行段后,126s时三级发动机开机,179s时三级发动机关机,至此,助推段结束,自由段开始。

针对上述场景,分别采用单个传统CS算法和本文算法进行弹道估计,以验证算法有效性。两种算法参数设置如下:

1)传统CS算法参数设置

机动频率0.01,最大加速度200m/s2。

2)非对称IMM算法参数设置

模型转移概率

模型初始概率

μ0=[0.5 0.5]

其中CS模型的机动频率为0.01,最大加速度为200m/s2,与用单个CS算法仿真时参数设置相一致,保证两次仿真的可比性。

2.2 结果分析

根据所设条件,利用上述两种算法进行估计,Monte Carlo仿真1000次,获得两种算法的位置、速度、加速度均方根误差(RMSE)如图5至7所示,图中,实线代表本文算法结果,虚线代表三维CS算法结果。图8为本文算法中两个子模型的平均概率曲线。

图5 位置估计RMSE

图6 速度估计RMSE

图7 加速度估计RMSE

图8 模型平均概率

图5给出了两种算法的位置估计RMSE。由图可知,经2s滤波稳定后,在助推段,本文算法在X轴、Y轴上的位置估计误差与三维CS算法相当,其中Z轴方向上因导弹机动性强,加速度较大,本文算法中精确动力学模型的影响增大,导致其估计误差略大于三维CS算法;在自由段,本文算法的估计误差明显小于三维CS算法,截至观测结束,本文算法的位置估计误差较三维CS算法,在X、Y、Z方向上分别下降了35.80%、34.85%、34.69%。

图6给出了两种算法的速度估计RMSE。可看出,本文算法在速度估计上的优势更明显:经2s滤波稳定后,助推段内,本文算法在X、Y方向上的速度估计误差与三维CS算法相当,同样,Z轴方向上因导弹机动性强,精确动力型模型的影响增大,导致助推段本文算法Z轴上的速度估计误差略大于三维CS算法;而在自由段,本文算法的优势明显,估计误差在X、Y、Z轴上分别下降了70.07%、67.64%、67.66%。

图7给出了两种算法的加速度估计RMSE。可看出,本文算法在加速度估计上效果最好,经2s滤波稳定后,助推段内,本文算法在X轴方向上的加速度估计误差与三维CS算法相当,Y轴、Z轴上因导弹机动性强,本文算法中精确动力学模型的影响增大,误差略大于三维CS算法;进入自由段后,本文算法的加速度估计误差明显下降,截至观测结束,较CS算法,在X、Y、Z轴上分别下降了84.01%、82.69%、82.10%。

同时由图5至7可看出,由于采用多模型决策,本文算法的稳定性明显优于三维CS算法。在124s二级发动机关机、176s三级发动机关机的这两个时刻,CS算法均产生较大的暂态误差,而本文算法平稳性明显较好,比如速度估计误差分别下降了34.7%、79.5%。

图8为本文算法中,两个子模型的平均概率曲线。由图可知,助推段内CS模型的平均概率高达0.8,明显大于精确动力学模型,自由段内精确动力学模型的平均概率高达0.8,明显大于CS模型。该结果与实际相符:助推内,CS模型更契合导弹的机动特性,因此CS模型对估计结果起主要作用;自由段内,精确动力学模型更契合导弹的非机动特性,因此其对估计结果起主要作用。由此说明,本文算法不仅能全程跟踪上升段弹道,更能通过概率曲线判断导弹的飞行状态,为进一步研究提供更多参数。

图8中126s-128s时,模型概率发生快速转变:CS模型的概率快速下降至0.3,EKF模型的概率快速上升至0.7。该转变表明算法检测出了124s-126s导弹短暂的滑行段,且模型切换延迟控制在了2s内,此时二级发动机关机,三级发动机还未开启,子模型概率的快速切换与导弹的运动特性相符。由此可得,本文算法的快速响应能力较好。

综上,基于非对称IMM算法的机动弹道估计不仅实现了弹道导弹整个上升段的稳定跟踪,且与传统的三维CS算法相比,自由段弹道估计精度提高了68.9%,且可有效检测导弹的运动模式切换,检测延迟小于2s,实现了导弹滑行段的精确检测,滑行段暂态误差降低79.5%。

3 结束语

针对弹道导弹的上升段弹道估计中,基于单个模型无法实现弹道导弹上升段全过程稳定跟踪的问题,本文提出了一种基于非对称IMM的机动弹道估计算法。该方法具有以下优势:

1)实现了弹道导弹上升段的稳定跟踪,且较三维CS算法,自由段估计精度较提高了68.9%,二三级发动机关机时刻的暂态误差分别下降34.7%、79.5%,算法稳定性较好。

2)能有效检测导弹的飞行状态,并通过概率曲线直观反映,切换延迟控制在2s,快速响应特征较好。

[1] 郑伟,汤国建.上升段引力常数变化及其对弹道导弹运动的影响[J].导弹与航天运载技术,2008(3):12-14.

[2] 李济生,叶杰,王家松,等.航天器轨道确定[M].北京：国防工业出版社,2003.

[3] Li X R.Survey of Maneuvering Tatget Tracking.Part1: Dynamic Models[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1333-1364.

[4] 钮俊清,单奇,任清安,等.跟踪弹道导弹全阶段的可变多模型方法[J].雷达科学与技术,2011,9(3):224-231.

[5] 任坚斌.基于交互式多模型的机动目标跟踪算法研究[D].南京：南京理工大学,2007.

[6] 周宏仁,敬忠良,王培德.机动目标跟踪[M].北京:国防工业出版社.1991.

[7] Shima T,Oshman Y,Shinar J.Efficient multiple model adaptive estimation in ballistic missile interception scenarios[J].Journal of Guidance,Control and Dynamics,2002,25(4)：667-675.

[8] 李晓宇,田康生,郑玉军,等.基于关机点状态的弹道导弹落点估计及误差分析[J].舰船电子对抗,2014,37(5)：71-74.

[9] Geoge M.S,Chen Guanrong,Wang Jianrong.Tracking an incoming ballistic missile using an extended interval kalman filter[J].IEEE Trans.On Aerospace and Electronic Systmes,1997,35(2):394-409.

[10] 杨元喜.Kalman滤波异常误差检测[J].测绘科学与工程,2005，25(4):1-4.

Ascent Trajectory Estimation Based on Asymmetric Interacting Multiple Model Algorithm

GENG Lin-yu1,2,WU Nan1,MENG Fan-kun1,HAN Jia-ying2

(1.Information Engineering University,Zhengzhou 450001;2.the Unit 96669 of PLA,Beijing 102208,China)

The ballistic missile rising section includes both the boost and the free segment,its complex dynamic characteristic is difficult for single model to achieve precise and stable tracking.This paper presents an adaptive asymmetric multiple model algorithm for the estimation of the ascent trajectory,unifies the model state vector,the model set is constructed by three-dimensional current statistical model and accurate dynamic model.Simulation results show that,the algorithm realizes the high precision tracking of the rising segment of the missile and the effective detection of the shutdown point,compared with the traditional CS algorithm,the estimation accuracy of the free trajectory is improved by 68.9%,and can effectively detect the missile motion mode,the detection delay is less than 2S,the sliding section the transient error is reduced by 79.5%.

maneuver trajectory estimation; asymmetric interacting multiple model; maneuver detection; stably tracking

TJ761.；E927.13

A

10.3969/j.issn.1673-3819.2017.05.025

1673-3819(2017)05-0120-06

2017-01-09

2017-03-29

耿林玉(1989-),女,江苏盐城人,硕士,助理工程师,研究方向为空天目标预警信息处理。