优化非等间距GM(1,1)灰色模型在沉降预测中的应用
徐连芳?丁欣


摘 要 在沉降预测分析方法中,灰色理论具有独特的特点,基于紧邻均值生成背景值的传统灰色预测模型,忽视了沉降发展的非线性特点,不能反映路基沉降变形的总体规律。在综合考虑实际工况中断面沉降点不等时距观测的基础上,分析模型传统计算方法误差产生的原因,通过同步优化灰导数和背景值并改进初始条件的方法,建立路基沉降预测的优化非等间距GM(1,1)模型。工程实例表明,优化的模型具有良好的拟合及预测精度,能够满足工程实际需要。
关键词 灰色模型;非等间距;优化;沉降;预测
Application of Optimized Non-equidistance GM (1,1)Grey Model inSettlementPrediction
XU Lian-fang1,DING Xin2
1.Zhenjiang Thorpe construction and Installation Engineering Co., Ltd., Zhenjiang 212000, China;
2.Engineering Construction Management of Runzhou District of Zhenjiang, Zhenjiang 212000, China
Abstract In the method of settlement prediction, grey theory has its unique characteristics.But the traditional grey prediction model generates the background value based on the nearest neighbor mean.It neglected the nonlinear characteristics of settlement development,which cannot reflect the general law of subgrade settlement deformation.On the basis of considering the unequal interval observation of the settlement points in the actual working conditions, analyzed the causes of the errors in the traditional calculation method.Through improved initial conditions by simultaneous optimization of grey derivative and the background value,established the optimized GM (1, 1) model for prediction of subgrade settlement.The analysis of an engineering example shows that it has good fitting and prediction accuracy and can meet the needs of practical engineering applications.
Key words Grey model; Non-equidistance; Optimization; Settlement; Prediction
路基沉降控制是软基道路质量的关键。在高等级公路施工中,为合理控制工期,常采用施工期的实测沉降观测资料预测预压期沉降-时间的关系,以优化设计工期。基于实测监测数据的沉降预测的方法主要有双曲线法[1]、对数曲线法[2]、指数曲线法[3]、灰色系统法[4]等。其中灰色系统预测模型具有显著的“小样本”、“贫信息”等特点[5],用于沉降预测有其独特优势。应用灰色模型预测沉降变形的方法已有学者进行过研究,主要集中在等时距单变量GM(1,1)模型、多变量MGM(1,n)模型及其改进模型[6-7]等,对非时距灰色模型的研究也主要是通过分段线性插值等等时距化进行处理[8-9],均与实际工况存在较大差异。
软土路基的沉降是一个复杂过程,受到工期、环境因素的影響,实际观测周期往往是非等间距的,周期间隔变幅大、加载数据高增长,这就对灰色模型的预测精度提出很高要求。本文采用原始序列直接累加生成非等间距灰色模型,从初始形式灰微分方程出发,通过同步优化灰导数和背景值的方法建立了优化非等间距GM(1,1)模型。工程实例计算表明,优化模型具有良好的拟合及预测效果。
3 工程实例应用
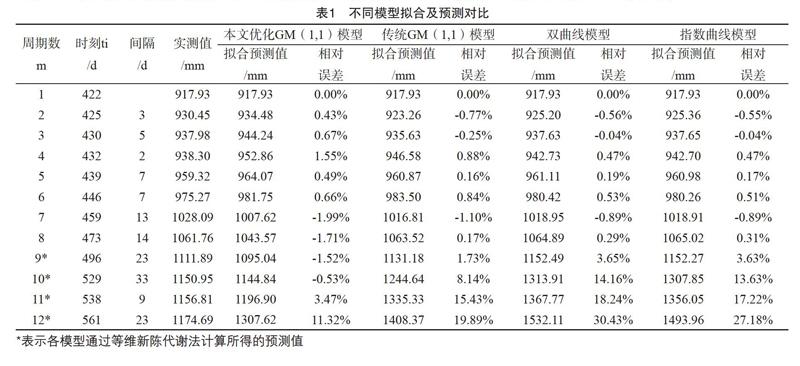
选取某工程2008年8月30日至2009年1月16日间共m=12期沉降观测序列作为分析目标(如表1),该断面为塑料排水板联合堆载预压加固软基。其中前8期用于建模,后4期用于检验预测精度。根据上述优化模型计算步骤,通过编制计算程序,求得沉降数据拟合值及预测值如表1,为便于比较,表中同样列出按传统紧邻均值生成背景值GM(1,1)模型、双曲线[1]及指数曲线模型[3]的计算结果。
由不同模型对前8期数据拟合结果显示,本文优化GM(1,1)模型、傳统GM(1,1)模型、双曲线模型、指数曲线模型的平均拟合相对误差分别为1.07%、0.60%、0.42%、0.42%,双曲线模型、指数曲线模型拟合效果最优,本文优化GM(1,1)模型拟合值平均相对误差较其他模型稍大些,但仍保持了较高的拟合精度,对各监测点每期拟合值依然达到了较理想的精度,相对误差基本控制在1%左右,单点拟合最大相对误差也仅为-1.99%。这表明本文采用的优化方法对于拟合效果是可行的,基本能够与其他模型保持在同等精度等级。
由后4期的预测值结果分析表明,优化GM(1,1)模型在拟合精度上虽不是最优,但在预测精度上明显优于其他三种模型,同期预测值相对误差均大幅低于其他模型,对9~11期沉降预测值与实测值的相对误差精度均控制在5%以内,达到良好等级,对第12期的预测相对误差开始明显增大,但也控制在15%以内,4期预测值平均误差仅为4.21%;双曲线模型和指数曲线模型虽然拟合精度较高,但在预测精度上明显较差,除对第1期预测尚算理想外,后续预测误差急剧增大,第12期预测误差均达到30%左右,4期预测值平均误差分别达16.62%、15.42%;传统GM(1,1)模型拟合及预测精度介于中间,预测值平均误差为11.30%。实际上,本文通过优化模型用1~8期共51天的实测数据有效预测了88天后的预测值,说明优化的模型在“小样本”、“贫信息”预测上有显著优势,短期内的预测效果变得更加理想,能够满足工程应用需要。
综合上述分析及数据计算表明,采用指数曲线和双曲线模型进行沉降预测时,观测周期的长短及时间间隔取值对沉降量预测的影响显著,其对沉降趋于稳定的后期阶段曲线具备良好的拟合精度,但对前期分级加载阶段沉降拟合不够稳定;且两种模型均对沉降曲线未来发展的整体变化趋势反应滞后,预测精度较差。无论采用何种模型,能够取得较长周期、较高精度的预测结果才是最终目标。而灰色模型具有显著的“小样本”、“贫信息”特点,在有限的数据信息条件下,能够较准确的描述沉降发展的整体趋势。但传统非等间距GM(1,1)模型基于紧邻均值生成背景值,忽视了沉降发展的非线性特点,对于一些步长变幅大、高增长的数据预测往往产生较大滞后误差。本文优化模型与传统GM(1,1)模型相比,通过基于灰导数优化的同步背景值优化方法,实际是对原始数据序列及累加序列进行了一次数据拟合,使得不规则的散点序列更加符合准指数特征,减少了个别监测数据异常变化的影响,能够充分体现原始数据序列的总体变化特征;对模型初始条件的优化实际上也是充分考虑了每一期监测值信息对未来预测精度的影响,使得模型更加符合原始数据序列变化的总体态势。
4 结束语
(1)本文在传统灰色模型基础上,从白化微分方程和初始形式灰微分方程出发,通过灰导数和背景值同步优化并改进初始条件的方法建立了优化的非等间距GM(1,1)模型。其特点是,改进后的灰微分方程与白化微分方程更加匹配,并充分考虑了每一期监测值信息对模型未来预测精度的影响,计算原理简单直接,增强了模型短期预测能力。
(2)通过工程实例应用表明,虽然优化模型在拟合精度上不是最优,但仍保持了较高的精度等级,其能够更好地反映沉降发展的整体态势和规律,在预测值精度上明显优于其他几种模型,更加体现灰色模型“小样本”、“贫信息”的预测特点,能够满足工程短期预测应用需要。
需要注意的是,路基沉降是一个复杂的非线性系统,利用实测数据进行未来沉降预测时,实测曲线的曲线特征是影响建模预测的关键。灰色系统预测沉降需要满足一定的条件,即实测数据序列整体变化趋势需满足非负准指数的特征,因此,改进的灰色模型对路基加载及加载结束后一定时期内的预测适应性较好;同时,对于受到环境因素干扰而失真及异常变化跳跃大的数据序列要对数据进行适当变换处理,以提高模型预测能力及精度。
参考文献
[1] 李健,李帅,喜文飞.双曲线模型在沉降监测预报中的应用[J]. 北京测绘,2012,(1):41-43.
[2] 王丽琴,靳宝成,杨有海,等.黄土路基工后沉降预测模型对比研究[J]. 铁道学报,2008,30(1):43-46.
[3] 王聪燚,余湘娟,高磊.考虑不同软基处理方式下路基沉降预测模型对比分析[J]. 科学技术与工程,2014,14(5):151-154.
[4] 柳治国,陈善雄,徐海滨.沉降预测的非等步長灰色时变参数模型[J].岩土力学,2004,25(12):1919-1923.
[5] 邓聚龙.灰色系统基本方法[M].武汉:华中科技大学出版社,2005.
[6] 劉寒冰,向一鸣,阮有兴.背景值优化的多变量灰色模型在路基沉降预测中的应用[J].岩土力学,2013,34(1):173-181.
[7] 张耀峰.动态灰色理论模型在路基沉降预测中的应用[J].公路,2010,(4):45-47.
[8] 尹晖,周晓庆,张晓鸣.非等间距多点变形预测模型及其应用[J].测绘学报,2016,45(10):1140-1147.
[9] 曾鼎文,吴浩中.优化的非等时距灰色模型在湖南高速公路路基沉降预测中的应用[J].公路工程,2013,38(4):269-272.
[10] 王钟羡,吴春笃,史雪荣.非等间距序列的灰色模型[J].数学的实践与认识,2003,33(10):16-20.
[11] 王正新,党耀国,刘思峰.基于离散指数函数优化的GM(1,1)模型[J].系统工程理论与实,2008,(2):62-67.
[12] 夏卫国,米传民,刘思峰,等.基于初值改进的多变量MGM
(1,m)模型研究[J].中国管理科学,2013,(21):81-85.
[13] 肖燕彩,陈秀海.多变量灰色预测公式的改进[J].数学的实践与认识,2009,39(6):98-101.

