改进遗传算法柔性作业车间调度

王 丹， 周连喆

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

改进遗传算法柔性作业车间调度

王 丹， 周连喆*

(长春工业大学 计算机科学与工程学院， 吉林 长春 130012)

提出一种新的遗传算法(NGA)解决FJSP的完工时间最小化问题。采用新染色体表示和不同交叉操作和变异操作策略，依据基准数据集和测试数据验证了NGA算法。

车间调度； 遗传； 交叉操作； 变异操作

0 引 言

作业车间调度问题(JSP)是生产调度和组合优化问题的一个分支。在经典的JSP中，任意一个工序只能由指定的某台设备加工，而在柔性作业车间调度(FJSP)中，则允许工序由一个机床集合中的任意一台加工。

柔性作业车间调度工作涉及到以下问题：分配工序机器(路径问题)和确定工序在机器上的加工顺序(排序问题)，以使得完成所有工序的时间最小化。进而，两决策相结合又呈现了额外的复杂性。因为FJSP被证明是NP-hard问题的JSP问题的扩展[1]，所以柔性作业车间调度问题是比JSP更复杂的NP-hard问题。

多年以来，为了解决FJSP，已经提出了许多算法，尤其是禁忌搜索、模拟退火、遗传算法、粒子群优化[2-5]。

在本研究中，提出了一种新的遗传算法(NGA)来解决FJSP的完工时间最小化问题。我们创建一个新的染色体表示方法，称为“置换工作”。

这种方法使我们能够找到一个新的个体工作的编码方案，并且它能考虑到各种约束的柔性作业车间调度问题。在同一时间，我们采用不同的交叉和变异算子的策略,计算结果表明，该算法是有效的。

1 定义和形式化问题

1.1问题描述

专注于由以下要素组成的柔性作业车间调度问题：

1)作业集合。J={J1,J2,…,Jn}是一组N个被安排的作业。每个作业集由一组预定的操作组成。Oij是作业Ji包含的nj道工序。所有的工件在零时刻都能被加工。

2)机器集合。M={1,2，…,m}是一组M台不同的机器。每台机器一次只能加工一个工件，并且每个工序一经开始就不能中断。所有机器在零时刻都可用。

3)灵活性。柔性作业车间调度问题分为两种类型如下：

①总调度(T-FJSP)：每个操作可以在M个在车间加工中现有的机器中的任何一个上进行。

②部分调度(P-FJSP)：每个操作可以在M个在车间加工中现有的机器中的其中一个上进行。

4)约束。限制可能的操作作业规则，它们可以被分类为以下条件：

①每个操作一次只能由一个机器加工(析取约束)。

②从开始到运行完成的每个操作(非抢占条件)。

③每个工件在某一时刻只能在一台机器上加工，不能中途中断(容量约束)。

④虽然各种工作操作之间不存在优先约束，但每个工作预定的操作顺序控制着下一个操作，每个工件的每道工序需要在前一道工序完成后才能进行加工(优先/连接约束)。

⑤机器的限制强调的是该操作仅可以被给定集合中的机器处理(资源约束)。

5)目的。一个时间表，找到完成所有作业的最小时间(最小完工时间)。

为了简化算法的演示，文中设计了一个FJSP样本实例。P-FJSP数据集包括两个作业在5台机器进行加工。每个格子中的数字表示在相应的机器上操作的处理时间见表1。

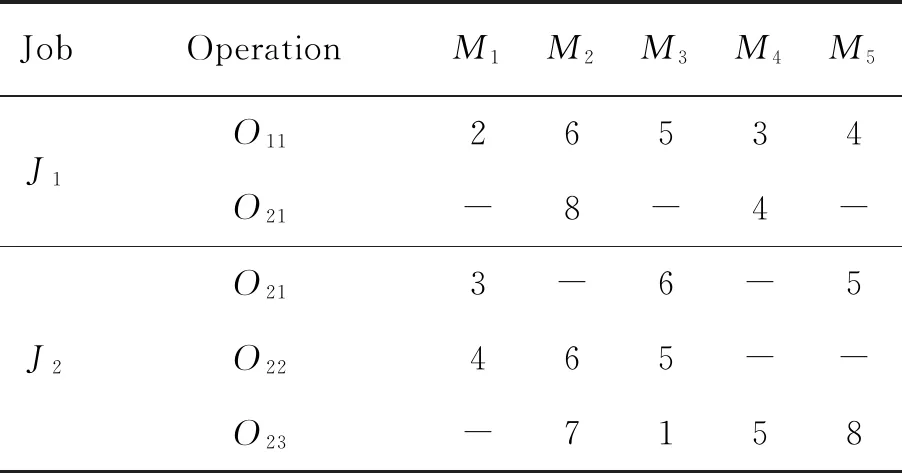
表1 一个P-FJSP实例的处理时间表

1.2问题制定

文中所需的变量如下：

Ω----所有机器集合；

n----总工件的数量；

m----总机器的数量；

i----第i个工件；

j----第j个工序；

Jio----工件i的总的工序数量；

Oij----工件i的第j道工序；

Ωij----工件i的第j道工序的可选加工机器数；

Pijk----工件i的第j道工序在第k个机器上的加工时间；

Sijk----工件i的第j道工序在第k个机器上加工的开始运作时间；

Eijk----第j种工件的第i道工序在第k个机器上加工的结束时间；

L----所有工件的总的工序数量；

H----非常大的正整数。

1.2.1 目标函数

设Ci是工件Ji的完工时间，则最大完工时间Cmax最小的目标函数为：

1.2.2 限制条件

∀i,j

Cij-Cij+H(1-Yijijk)+H(1-Xijk)+

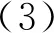
Cij-Cij+H(Yijijk)+H(1-Xijk)+

约束方程(2)规定完成时间和操作开始时间之间的差值等于其分配机器的处理时间。约束方程(3)及(4)确保不在同一台机器上同时处理任何作业。这个析取约束方程(3)变为非活动状态时和析取约束方程(4)变得不活跃时，约束方程(5)确保操作的开始时间总是积极的。约束方程(6)表示工序之间的先后关系的各种操作。约束方程(7)规定同一台机器同一时刻只能加工一个工件[16]。Xijk：工件i的第j道工序在机器k上加工的判别条件，如果工件i的第j道工序在机器k上加工，则Xijk=1，否则Xijk=0。它表示工件i的第j道工序只能选择在可选机器集中的一台机器上加工。Yijijk：机器k加工工序的判别条件。它表示任一确定时刻，机器k不能同时加工任意两个不同的工件，也不能同时加工任意两道不同的工序。

2 一种新的柔性作业车间调度问题的遗传算法

2.1基本遗传算法

遗传算法是基于自然选择和遗传学原理的搜索方法[16-17]。它是一类借鉴生物界的进化规律(适者生存，优胜劣汰遗传机制)演化而来的随机化搜索方法。遗传算法使用主要操作，即交叉和变异，以找出全部最佳个体。交叉允许不同的解决方案(染色体)和突变增加的品种之间的交换信息。在选择和评价的初始种群之后，染色体被选中，并应用交叉和变异算子。然后，新的个体形成,这个过程一直持续达到终止条件为止[19-20]。

2.2染色体表示

染色体表示有一个组成部分，也就是作业排列(JP)。用一个长度等于L的整数数组，每个整数的值等于相应作业的数组索引。染色体取决于以下两个组成部分：

关于操作的顺序部分，使用一个长度等于L的整数数组，每个整数的值等于相应的作业序列数组的索引。关于机器序列部分，还可以使用等于L的相同的长度。例如，因为在变化的机器集数组中这个值是1，所以M1选择运行操作O21。因为操作O21可以在两台机器(M1和M3，并且有效值是1和3)上运行，所以数组中的值也等于1。

2.3遗传算子

2.3.1 选择算子

为繁殖选择个体是选择的任务[21]。选择是从群体中选择优良个体、淘汰劣质个体的操作。文中采用的选择方法的详细步骤如图1所示。

图1 选择算子程序

2.3.2 交叉算子

交叉的目标是通过交换目前获得的好的信息以获得更好的染色体来改善结果。交叉操作是将种群中的两个个体交换某些基因，产生新的基因组合。在这项研究中，使用了两种交叉算子的染色体。

根据所采用的表示，在这项研究中使用的两种交叉算子为均匀交叉和基于保序的交叉(POX)。均匀交叉操作描述如图2所示。

图2 交叉算子程序

2.3.3 变异算子

突变引入额外的变异性，以提高个体的多样性。通常情况下，突变只是小概率的出现。大概率可能破坏良好的染色体。在本研究中提出了一种变异算子，它是染色体PJ值突变，值突变工作过程如图3所示。

图3 变异算子程序

所提出的算法描述如图4所示。

图4 新的遗传算法操作流程

2.4算法的性能验证

提出的新算法通过Brandimarte数据集(BR数据)来测试。该数据集包括10个问题，其中作业数量从10到20不等，机器数量从4到15不等，每个作业的操作数从5到15不等。

提出的新算法与下面的算法相比较见表2。

M&G：由Mastrolilli和Gambardella提出的方法。

GENACE：由Ho和Tay提出的方法。

Zhang:由张国辉和高玲提出的方法。

Chen:陈H和伊洛J提出的方法。

Pessella：Pezzelle和Morganti提出的方法。

HGTS：由J.J.Palacios和A.Gonzalez提出的方法。

针对FSJ问题提出的NGA算法在MATLAB编码和运行在P4CPU，主屏2.3GHz，记住下列参数：popsize=100，PC=0.8，PM=0.05，选择百分比=30%。

表2列出了问题的名称、问题的维数(工作号×机器号)，最好的已知的解决方案(Cm)，通过文中的算法得到的解(NGA)和每个其他算法得到的解。计算结果表明，所提出的遗传算法，到目前为止，是寻找速度最佳的解决方案。在10个测试问题中，Mk01能获得在所有的方法中较好的解。通过使用NGA，Mk03和Mk08可以在第一代获得最优解。Mk02，Mk04，Mk05和Mk09(4个问题)可能具有和M&G方法同样良好的结果。对于一个问题，mk06可以得到和GENACE相同的结果，并且两个问题(Mk07，MK10)可以获得和Chenetal同样的结果。

3 案例研究问题

文中考虑了现实世界的应用----一个药物公司的调度问题。Saidal集团是Algeria领先的制药企业之一。该公司生产各种药物。每个产品都可以被视为一种工作。因此，在这个问题上考虑了10个工作。这个部分在机器中产生。这个机器设置尺寸为31。

参与工作的药品见表3。

加工时间是一台机器在不同阶段加工所需的时间。每台机器的处理时间是多次测量的，平均时间是在这项工作中采取的。在不同的机器上所有10个工作的处理时间(10-3s)见表4。

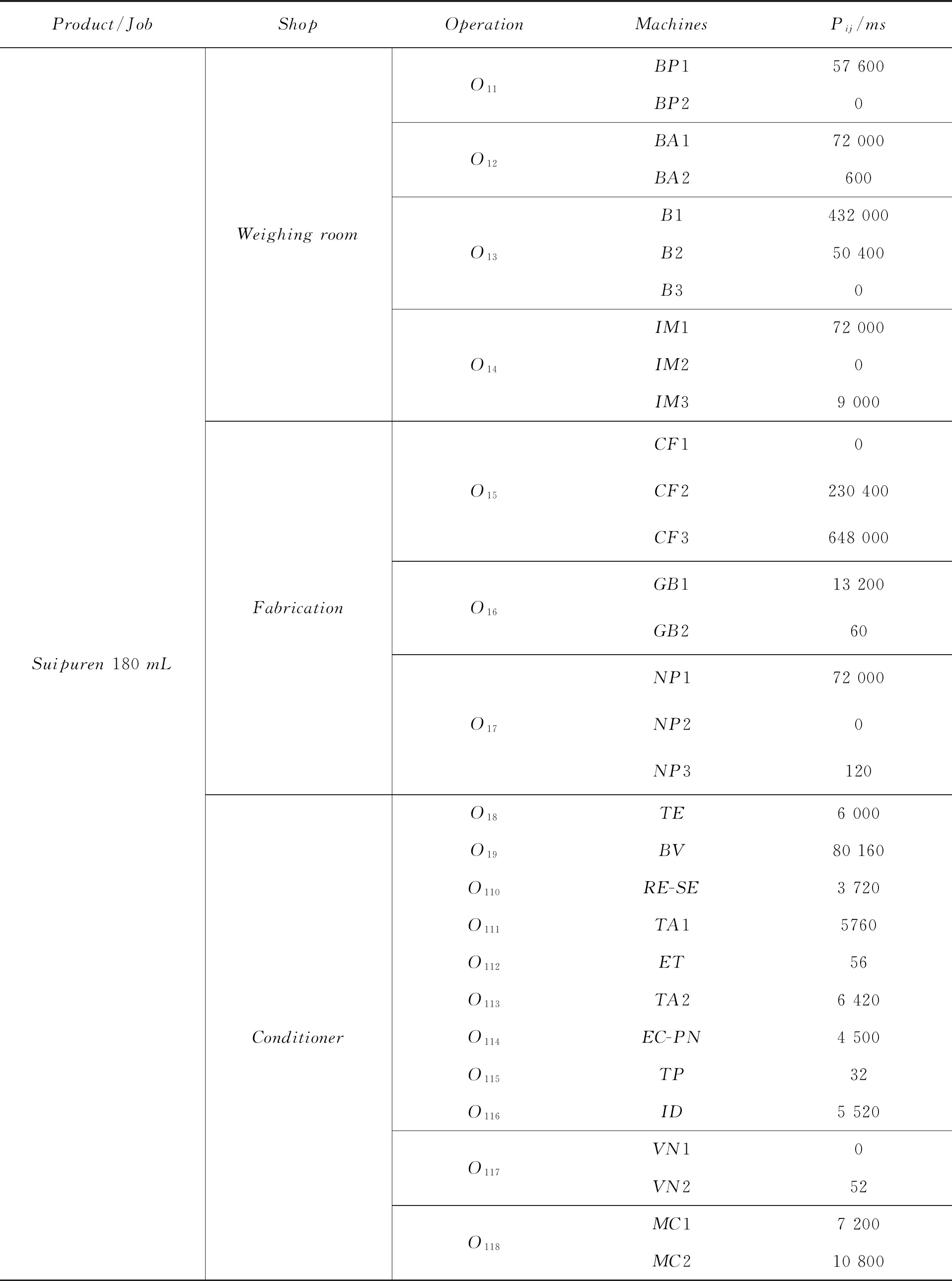
表4 3个车间和不同的机器上作业分配的例子

3.1结果

为了获得有意义的结果，在同一个实例上运行文中算法5次。为了在一个可以接受的时间跨度得到满意的解，NGA中使用的参数要实验性地进行选择。根据问题的复杂性，有效遗传算法的种群规模从50到150不等。

最初，我们检查了在图5～图7中方法的性能。然后得出平均最好的完工时间。

最小完工时间(company)如图8所示。

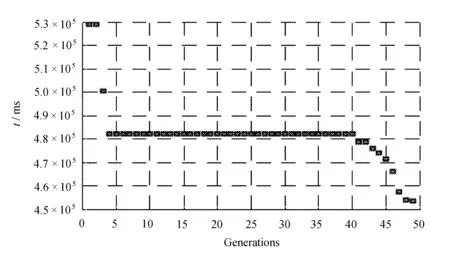
图5 最小完工时间减少(Weighingroom)

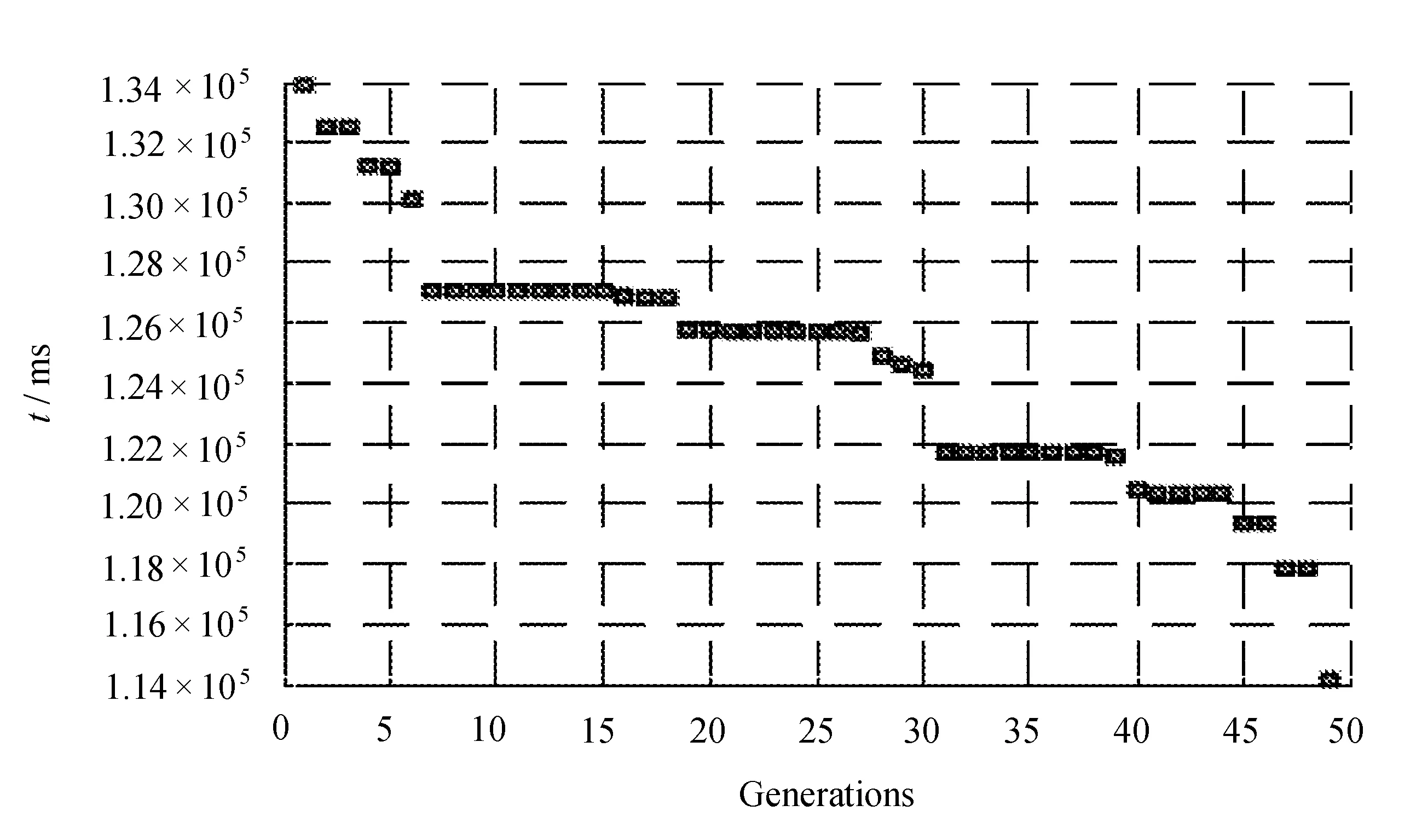
图6 最小完工时间减少(Fabrication room)

图7 最小完工时间(conditioner shop)

图8 最小完工时间(company)

在图8中，可以看出平均最好完工时间在减少。

最优解的甘特图如图9～图11所示(本公司制造车间和空调车间)。

在SAIDAL和NGA之间最小完工时间比较如图12所示。

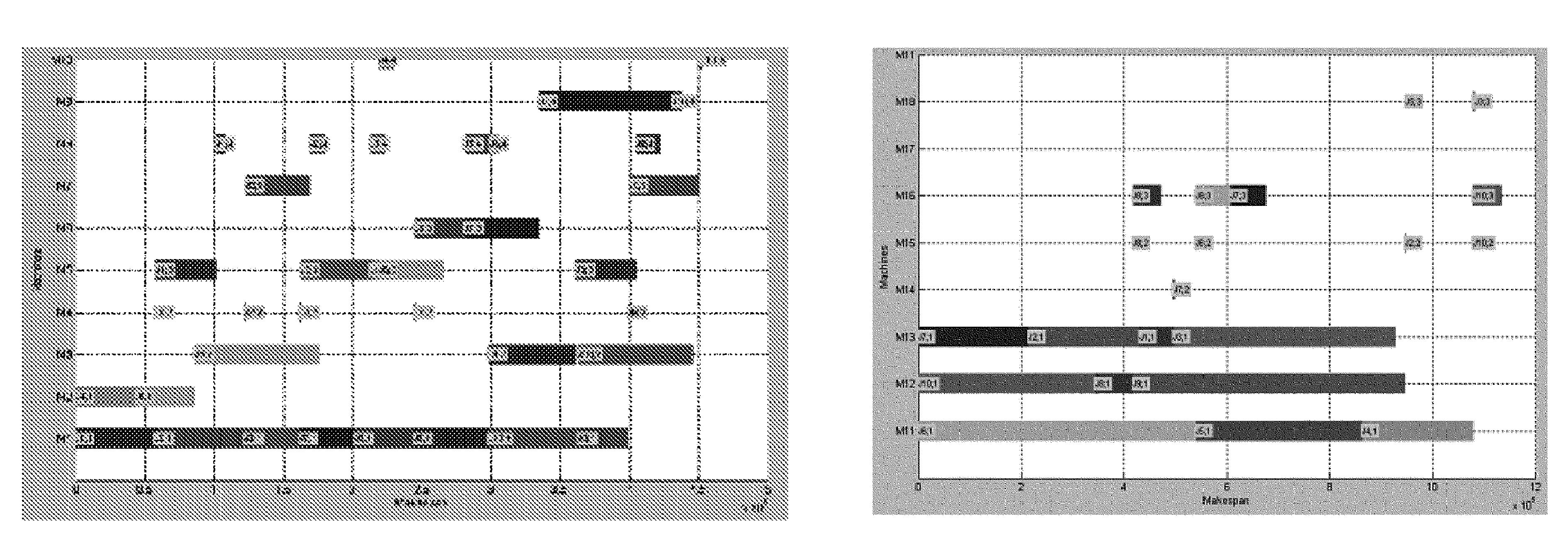
图9 甘特图(weighingroom) 图10 甘特图(fabricationshop)

图11 甘特图(conditioner shop)

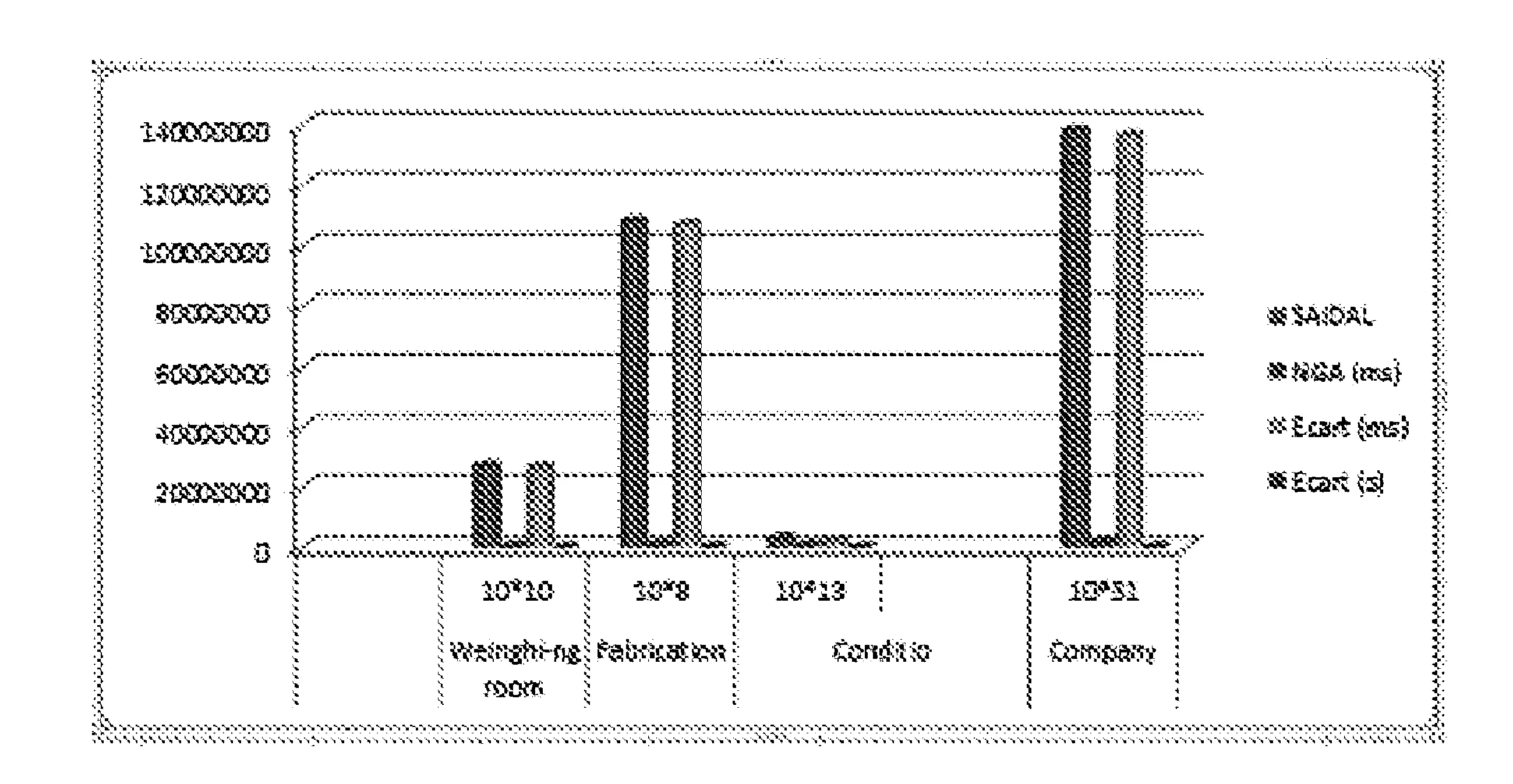
图12 SAIDAL和NGA之间最小完工时间比较

最后，整个公司的甘特图如图13所示。

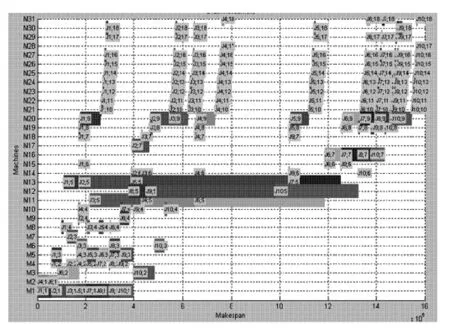
图13 整个公司的甘特图

3.2附加性能评价

进行了一系列的实验来评估所提出的NGA算法的性能。设计的各因素水平和最佳的完工时间比较见表5。

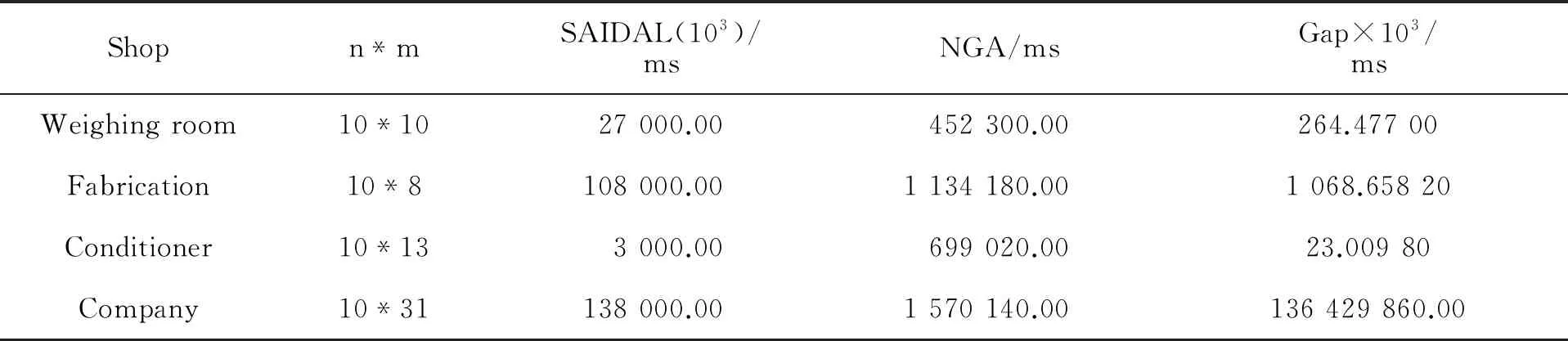
表5 SAIDAL和NGA之间最小完工时间比较

根据研究结果，为提出的遗传算法提供了最佳的计算时间的结果(文中方法和该公司的处理时间之间的差距图形见图12)。

4 结论与未来研究

提出了一个新的染色体表示方案和各种交叉和变异算子策略。此外，从参考文献的实例来看，该算法已经过测试，我们用属于药品制造公司的真实的应用数据检查了该算法。计算结果表明，文中提出的新的遗传算法(NGA)有效地解决了FJSP问题。

在未来的研究中，我们打算在优化算法和解决方案的过程中考虑多个目标，如预定时间、平均流量时间的要求和如更换工具类似的其他约束。

[1] M R Garey, D S Johmson， R Sethi. The complexity of flow shop and job shop scheduling[J]. Mathematics of Operational Research,1976(1):117-129.

[2] P Brucker, R Schile. Job-shop scheduling with multipurpose machines[J]. Computing,1990,45(4):369-375.

[3] P Brandimarte. Routing and scheduling in a flexible job shop by tabu search[J]. Annals of Operations Research,1993,41:157-183.

[4] H Chen, J Ihlow, C A Lehmann. Genetic algorithm for flexible Job shop scheduling[J]. IEEE International Conferenceon Robotics and Automation Detroit,1999(2):1120-1128.

[5] I Kacem, S Hammadi, P Borne. Approche by localization and multiobjective evolutionary and optimization for flexible job shop scheduling problems[J]. IEEE Transations Man and Cybernetrics,2002,32(1)：1-13.

[6] N B Ho, J C Tay. GENACE: An efficient cultural algorithm for solving the flexible job shop problem[J]. Proceeding of IEEE Congress on Evolutionary Computation,2004(1):1759-1766.

[7] H P Zhang, M Gen. Multistage-based genetic algorithm for flexible job shop scheduling problem[J]. Journal of Complexity International,2005,48:409-425.

[8] P Fattahi, M S Mehrabad, F Joli. Mathematical modeling and heuristic approaches to flexible job shop scheduling problems[J]. Journal of Inteligent Manufacturing,2007,18:331-342.

[9] B S Girish, N Jawahar. Scheduling job shops associated with multiple routings with genetic and ant colony heuristics[C]//[S.l.]:Thiagarajar College of Engineering,2008.

[10] F Pezzela, G Margenti, G Ciaschetti. A genetic algorithm for flexible job shop scheduling problem[J]. Computers and Operations Research,2007,35(10):3202-3212.

[11] W Sun, Y Pan, X Lu, et al. Research on flexible job shop scheduling problem based on a modified genetic algorithm[J]. Journal of Mechanical Science and Technology,2010,24(10):2115-2119.

[12] A Motaghedi, K Sabri Laghare, M Heydari. Solving flexible job shop scheduling problem with multi objectives[J]. International Journal of Industrial Engineering and Production Research,2010,21:197-209.

[13] G Zhang, L Gao, Y Shi. An effective genetic algorithm for the flexible job shop scheduling problem[J]. Expert System with Application,2011,38:3563-3573.

[14] Q Zhang, H Manier, A Manier. A genetic algorithm with tabu search procedure for flexible job shop scheduling with transportation constants and bounded proceding times[J]. Computers and operations Research,2012,39:1713-1723.

[15] J C Chen, C C Wu, C W Chen. Flexible job shopwith parallel machines using genetic algorithm and grouping genetic algorithm[J]. Expert Systems with Application,2012,39:10016-10021.

[16] N Kim, H Kim, J Lee. Damage detection of truss structures using two stage optimization based on micro genetic algorithm[J]. Journal of Mechanical Science And Technology,2014,28(9):3687-3695.

[17] R N Yadar, V Yadar, G H Singh. Application of non dominated sorting genetic algorithm for multi objective optimization of electrical discharge diamond face grinding process[J]. Journal of Mechanical Science and Technology,2014,28(6):2299-2306.

[18] L N Xing, Y U Chen, K W Yang. Multi population interactive coevolutionnary algorithm for flexible job shop scheduling problems[C]//Comput. Optim. Appl., DOI 10.1007//S 10589-009-9244-7,2009.

[19] F N Defersha, M Chen. A coase-grain parallel genetic algorithm for flexible job shop scheduling with lot streaming[C]// In IEEE International Conference on Computational Science and Engineering,2009.

[20] Y K Park, J M Yang. Optimization of mixed casting processes considering discrete ingot sizes[J]. Journal of Mechanical Science and Technology,2009,23:1899-1910.

[21] S F Hwang, Y Hsu, Y Chen. A genetic algorithm for the optimization of fiber angles in composite laminates[J]. Journal of Mechanical Science and Technology,2014,28(8):3163-3169.

Flexiblejobshopschedulingbasedonimprovedgeneticalgorithm

WANG Dan, ZHOU Lianzhe*

(School of Computer Science & Engineering, Changchun University of Technology, Changchun 130012, China)

A new genetic algorithm (NGA) is put forward to solve the minimized completion time for FJSP. We apply a new chromosome representation and adopt different crossover operations and mutation operation. The algorithm is verified based on both the benchmark and tested data sets.

FJSP； genetic algorithm； crossover operator； mutation operator.

TP 18

A

1674-1374(2017)04-0361-10

2017-04-15

王 丹(1989-)，女，汉族，河南信阳人，长春工业大学硕士研究生，主要从事人工智能应用方向研究,E-mail:wd1037407198@163.com. *通讯作者：周连喆(1971-)，女，汉族，吉林长春人，长春工业大学副教授，主要从事人工智能与数据挖掘方向研究,E-mail:zhoulianzhe@ccut.edu.cn.

10.15923/j.cnki.cn22-1382/t.2017.4.08