双馈风电机组低电压穿越非线性变结构控制策略研究

高鲁峰， 王奔， 李晓， 张锐

(西南交通大学 电气工程学院，四川 成都 610031)

双馈风电机组低电压穿越非线性变结构控制策略研究

高鲁峰， 王奔， 李晓， 张锐

(西南交通大学 电气工程学院，四川 成都 610031)

提出一种基于精确线性化变结构控制的双馈感应风力发电机(DFIG)的低电压穿越控制器设计方法。建立了DFIG在同步旋转dq坐标系下的非线性数学模型，在此模型基础上，采用精确线性化将原非线性系统模型转化为线性系统模型。应用变结构控制原理设计DFIG的发电机转子侧及电网侧变流器的控制器，同时通过PI控制以稳定直流侧电容电压。最后，利用MATLAB仿真软件搭建了6×1.5 MW的DFIG系统仿真模型，仿真结果表明，所设计的控制器能够在电压跌落后抑制转子过电流以及直流母线过电压现象，实现了DFIG的低电压穿越。

双馈感应风力发电机；电压跌落；低电压穿越；精确线性化；变结构控制

0 引 言

双馈感应风力发电机(Double-Fed Induction Generator，DFIG)并网运行时，定子绕组直接与电网相连，当电网出现故障导致发电机出口端电压骤降时，由于定子磁场的耦合作用，在转子侧会感应出较大的过电流，同时对接在发电机转子侧的变流器造成严重影响，特别是引起变流器直流母线过电压[1]。因此风力发电机的低电压穿越(Low Voltage Ride Through，LVRT)能力是一个需要解决的问题。

电网故障或扰动导致DFIG并网点电压跌落，确保风电机组安全的同时，在电压跌落范围内，风电机组继续并网运行称为风力发电机的低电压穿越。本文主要研究电压对称跌落DFIG的低电压穿越控制策略。

文献[2-3]采用PI控制，其控制器设计简单，但参数整定复杂，增加了设计难度。文献[4-5]采用定子磁链法，这种控制方法的不仅能应对三相对称故障，在不对称故障时同样能达到控制目标，但是这种方法的复杂性增加了设计难度。文献[6-7]增加转子侧撬棒电路以保证变流器安全，但撬棒电路在工作期间，DFIG将运行在异步电机状态，从而吸收大量的无功功率，不利于电网电压的恢复。撬棒电路电阻值的选取对控制效果影响明显，通常是通过仿真和实验选出合适的阻值[8]。

本文根据DFIG的数学模型，通过精确线性化将原非线性系统转化为线性系统，并应用鲁棒性更为优越的变结构原理来设计LVRT时变流器的控制器。最后，利用MATLAB搭建仿真模型，验证所提出控制策略的正确性及有效性，实现电网电压跌落后，抑制变流器直流母线过电压和发电机定转子过电流现象。

1 DFIG数学模型

1.1 风力发电机数学模型

DFIG系统模型如图1所示

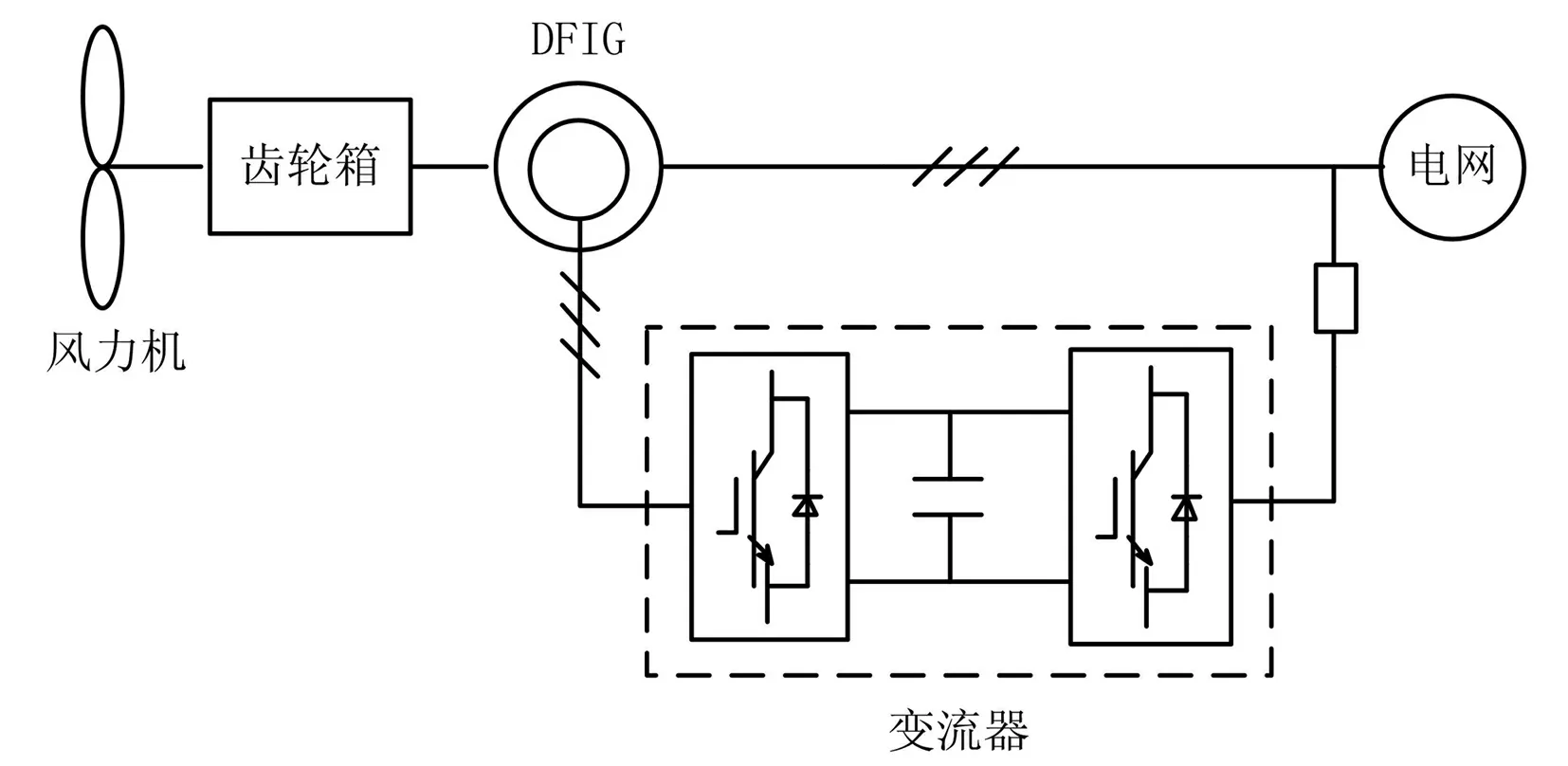
图1 DFIG系统模型

在同步旋转dq坐标系下，根据DFIG的工作原理及坐标变换，将定子电压定向到d轴后得[9]：

(1)

其中

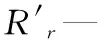
1.2 变流器电网侧数学模型

变流器电网侧主电路如图2所示。

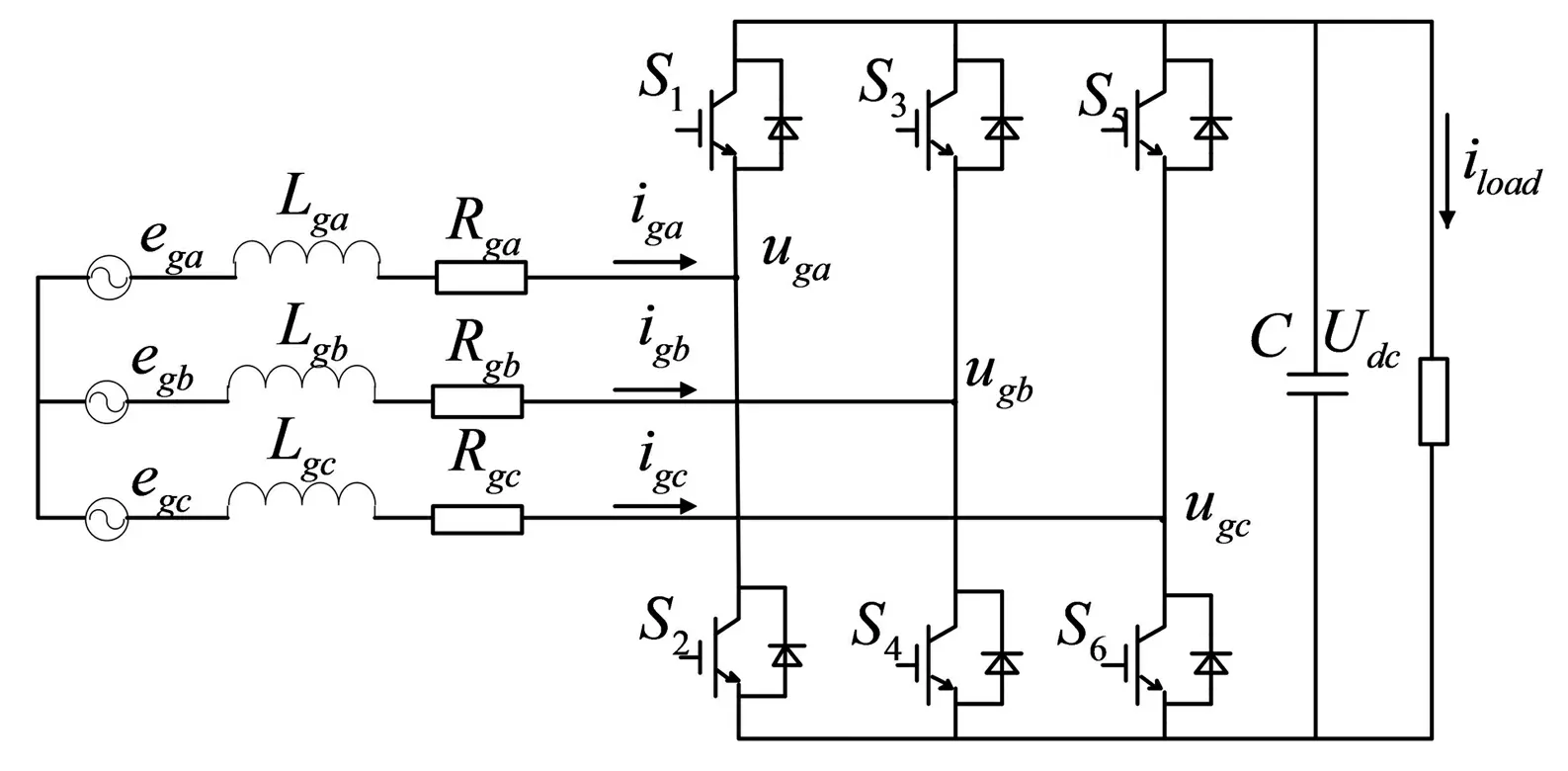
图2 变流器电网侧主电路

其在同步旋转dq坐标系下的数学模型如下式：

(2)

其中egd，egq—三相电网电压dq分量；igd,igq—流入变换器电流的dq分量；ugd，ugq—变换器交流侧电压dq分量；Rg—每相进线电阻的阻值；Lg—每相进线电抗器的电感；Udc—变流器直流侧电容电压；Pg—电网侧变流器的有功功率；Pr—发电机转子侧变流器的有功功率；

电网电压定向到d轴时有:egd=Eg，egq=0。Eg为电网相电压幅值。

将定子电压定向到d轴时，定子输出有功、无功功率和转子电流之间的关系如下式所示[10]:

(3)

2 DFIG低电压穿越控制器设计

2.1 系统模型的精确线性化

为便于应用微分几何法对系统进行精确线性化处理，令：

联立式(1)和式(2)，得仿射非线性标准形式:

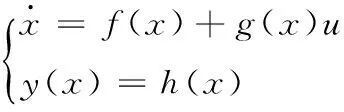
(4)

其中

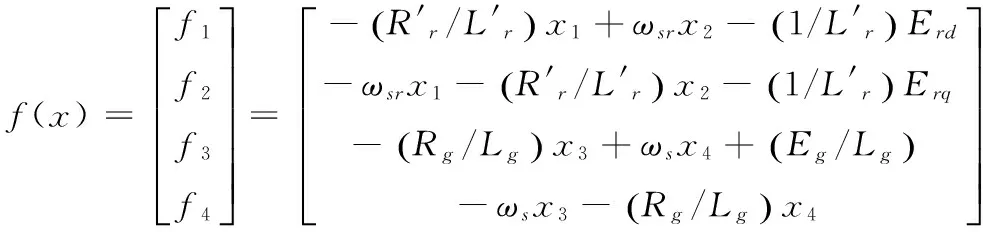
考虑到电网电压跌落、转子侧功率不平衡以及维持变流器直流侧电压稳定，选取系统控制输出量为Ps，Qs，igd，igq，则y(x)可以写成：

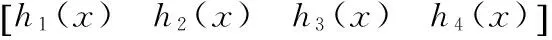
(5)

为了对DFIG模型精确线性化，首先要验证该模型是否满足精确线性化条件。根据精确线性化原理，对于式(4)求取输出y(x)的各阶不等于零的李导数，求解过程及结果为:

(6)

根据所求李导数的结果与系统关系度可知，对于系统的四个输出y(x)对应的关系度均为1，所以该控制系统的关系度集合为r=[r1r2r3r4]=[1 1 1 1]，且r=r1+r2+r3+r4=4，关系度总数与系统阶数相等，因此精确线性化条件成立。

根据李导数的求解结果，有矩阵：

根据精确线性化设计原理及坐标映射选择原则，可以求出以下坐标变换Z=Z(x)为：

(7)

因此，在新坐标系Z=Z(x)下的原系统状态方程转化为线性标准型：

(8)

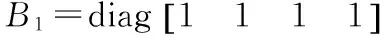
v=[vi]T=[Lfhi(x)+Lghi(x)·u]T，i=1，2,3,4；

则新控制量v和原控制量u的关系如下：

v=α(x)+B(x)u

(9)

由式(9)得:

u=B(x)-1(-α(x)+v)

(10)

其中

(11)

上式即为系统精确线性化之后线性系统控制量v与原非线性系统控制量u的关系。由此系统化为4个子系统，非常方便应用变结构控制理论设计控制器。

2.2 变结构控制器的设计

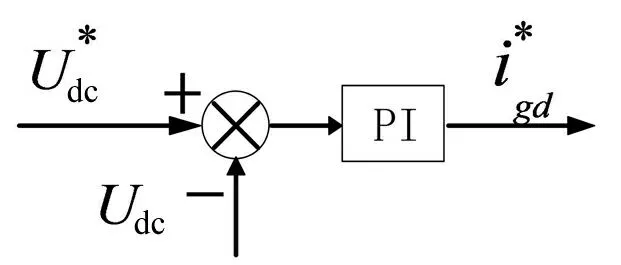
图3 电压外环控制

根据变结构控制理论，选取指数趋近率来设计系统的控制律[11-12]。因此取四个切换面分别为：

(12)

变结构指数趋近率为：

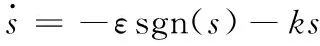
(13)

其中ε和k为变结构控制率的调节参数,sgn(·)为符号函数。

联立式(8)、式(12)和式(13)得:

(14)

由式(3)、式(11)、式 (14)得到采用精确线性化变结构控制器实现双馈风电机组LVRT转子侧与电网侧变流器控制原理框图分别如图4和图5所示。

图4 转子侧低电压穿越控制框图

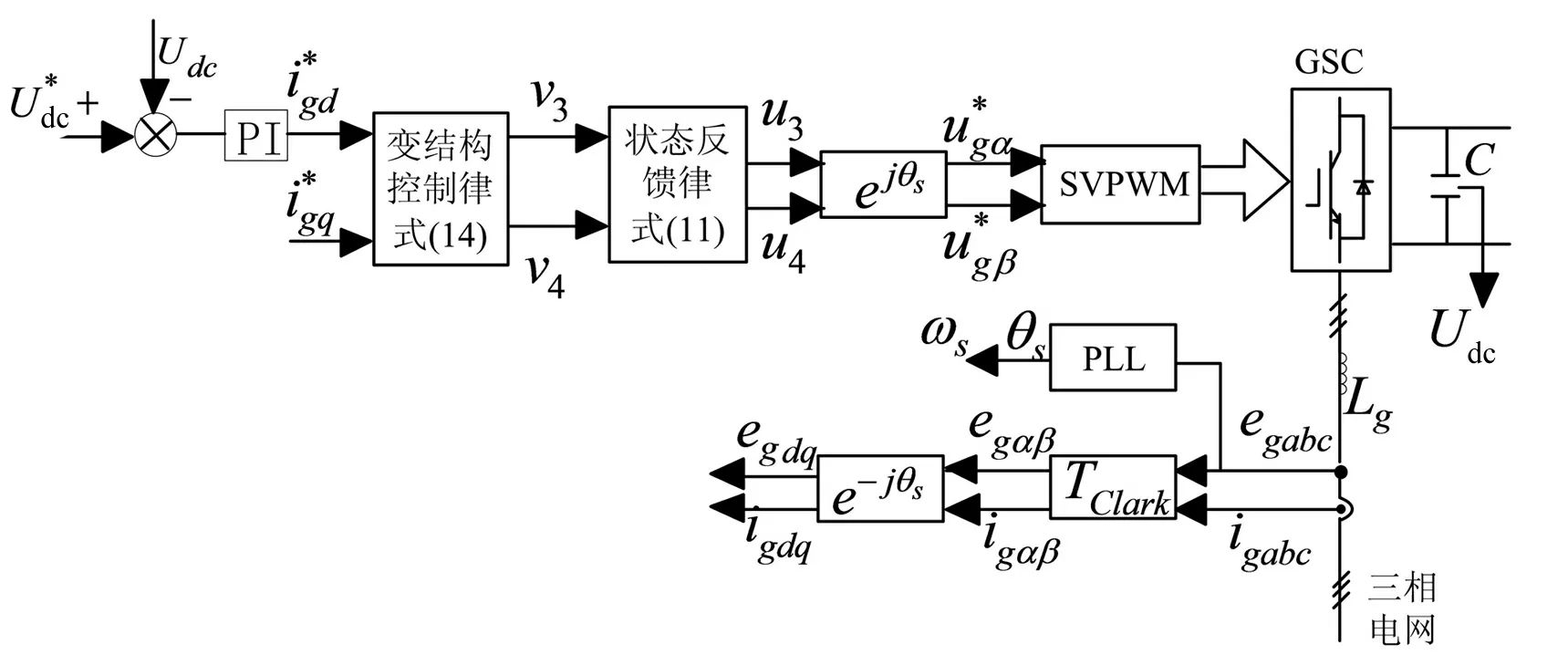
图5 电网侧低电压穿越控制框图

3 仿真验证

设故障后电压Us2=bUs，0≤b≤1，则低电压穿越过程中有功功率和无功功率参考值变为：

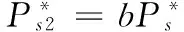
(15)

根据并网导则，在电压跌落后，风电场应输出无功功率以支撑电网电压恢复，且规定输出无功电流:IT≥1.5×(0.9-UT)IN。本文设置电压跌落50%，即UT=0.5 pu，则有：UNIT≥0.6UNIN，输出无功功率Qs2≥0.3S0，所以本文取K=0.3。

为验证控制器的有效性，本文基于MATLAB建立了仿真模型进行仿真验证。 DFIG系统仿真参数如表1所示。

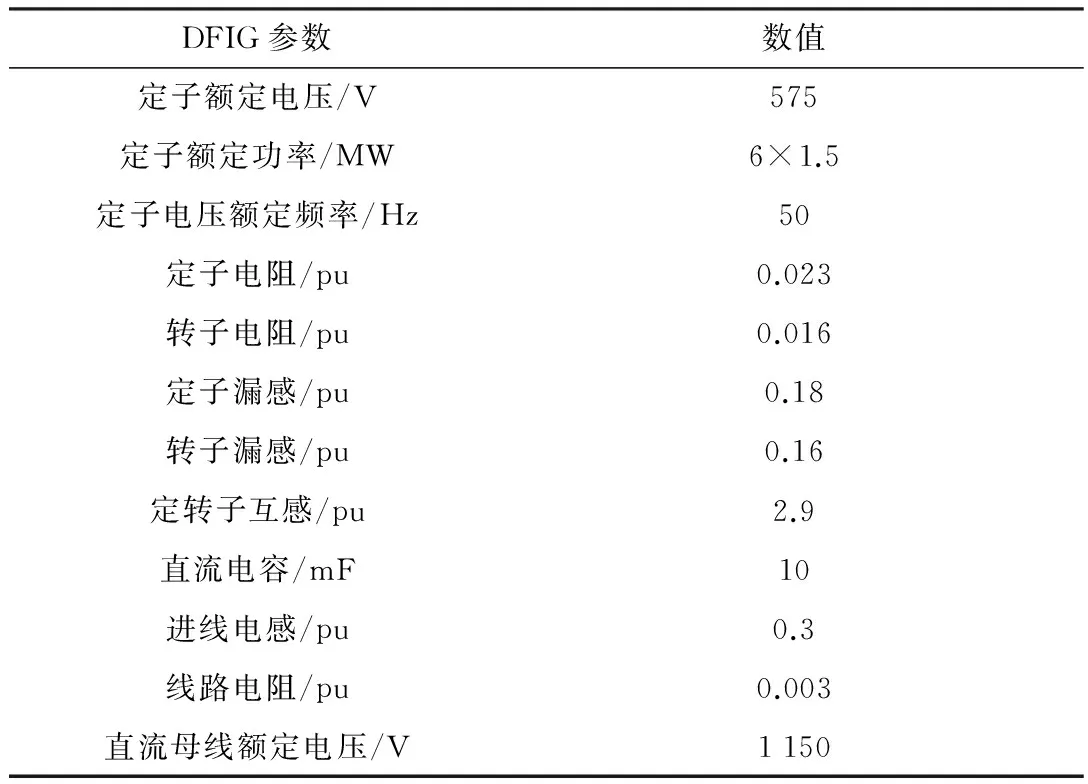
表1 DFIG系统仿真参数

4 精确性化变结构控制策略仿真分析

图6给出了基于精确线性化变结构控制策略和传统PI控制策略下仿真结果的对比图。

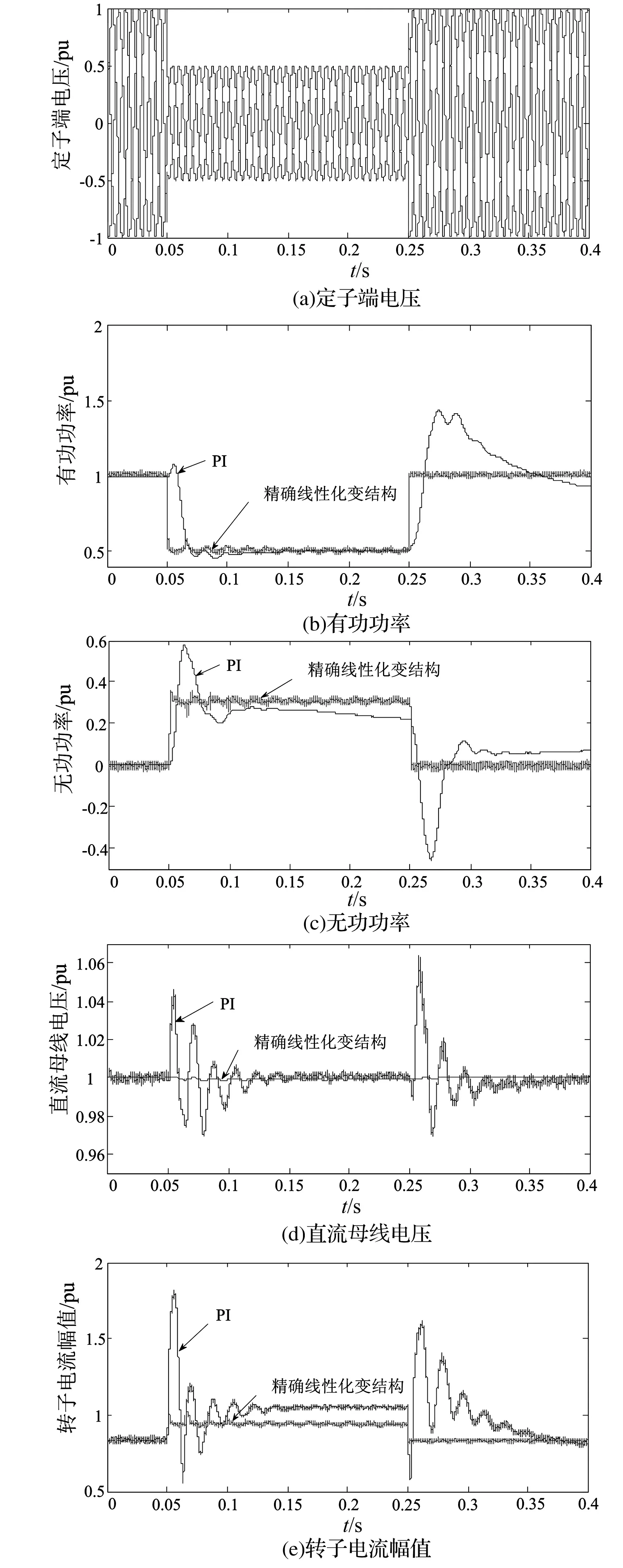
图6 反馈线性化变结构控制仿真结果

在PI控制策略下，定子端电压跌落到0.5 pu时(a)，系统有功功率逐渐跟随参考值，在故障后0.05 s稳定，定子端电压恢复时，有功功率明显超调(b)，引起转子过电流；系统在故障后为电网提供0.25 pu左右的无功功率支撑(c)，但电压恢复时，系统从电网吸收无功0.5 pu左右(c)，这不利于电压恢复。故障前后直流母线电压波动幅度均在7%左右(d)；在电压恢复瞬间，转子电流幅值达到稳态值的2倍以上(e)，长时间的转子过流将导致变流器损坏。

在精确线性化变结构控制策略下，定子端电压跌落到0.5 pu时(a)，系统有功功率迅速减小到0.5 pu左右(b)，且故障消除后，有功功率没有出现超调，避免了转子过电流，同时能够为电网提供0.3 pu的无功功率支撑(c)，在电压恢复时，无功功率为0，从而防止系统从电网吸收无功，避免了不利于电压恢复的问题。直流母线电压保持恒定1.0 pu左右(d)，转子电流幅值上升是因为系统向电网提供无功功率导致(e)，但并未超出安全界限。

5 结束语

本文首先采用微分几何理论将多输入多输出的非线性系统的数学模型进行精确线性化，得到线性标准型，在此基础上，采用鲁棒性更强的变结构控制理论来最终完成变流器的控制器设计。通过仿真分析表明：

(1)采用精确线性化方法，虽然其数学理论推导过程较为复杂，但对系统参数依赖性弱，且通过对比传统PI方法，精确线性化后的系统能更真实的反映原非线性系统。通过变结构理论设计的控制器比传统PI控制器具有更快的动态响应能力。

(2)通过本文提出的精确线性化变结构控制方法设计的控制器，在最大限度的输出有功功率的同时向电网提供一定的无功功率以支撑电压恢复。

(3)在电压跌落时，有功功率迅速减小，避免了转子过电流，电压恢复后，系统功率迅速恢复到稳态运行时的状态，仅有轻微的超调，表明本文控制策略较传统PI能够更有效的抑制发电机转子过电流和变流器直流母线过电压。

[ 1 ] 徐海亮, 章玮, 贺益康,等. 双馈型风电机组低电压穿越技术要点及展望[J]. 电力系统自动化, 2013, 37(20):8-15.

[ 2 ] 张隆, 杨俊华,吴捷. 基于自抗扰矢量控制的DIFG系统低电压穿越策略[J]. 电机与控制应用, 2015,28(10): 6-11.

[ 3 ] YANG L, XU Z, OSTERGAARD J, et al. Advanced control strategy of DFIG wind turbines for power system fault ride through[J]. IEEE Transactions on Power Systems, 2012, 27(2):713-722.

[ 4 ] 吴国祥, 刘鸿泉,顾菊平,等.基于磁链追踪的双馈风力发电系统低电压穿越[J]. 电测与仪表, 2016, 53(7):61-65.

[ 5 ] LIMA F K, LUNA A, RODRIGUEZ P A. Rotor voltage dynamics in the doubly fed induction generator during grid faults[J]. IEEE Transactions on Power Electronics,2010, 25(1): 118-130.

[ 6 ] 凌禹, 高强,蔡旭.紧急变桨与撬棒协调控制改善双馈风电机组低电压穿越能力[J].电力自动化设备, 2013, 33(4):18-23.

[ 7 ] 姚兴佳, 董鹤楠, 刘颖明,等. 基于撬棒保护的双馈风力发电机组低电压穿越控制策略研究[J]. 可再生能源, 2013, 31(2):52-57.

[ 8 ] 姜惠兰, 姜哲, 李天鹏,等. 风机转子撬棒投切对电力系统暂态稳定性的影响[J].电网技术, 2016, 40(8):2383-2388.

[ 9 ] 赵霞等. 双馈感应风力发电系统低电压穿越控制策略研究及其分析[J]. 电力系统保护与控制, 2015,42(16): 57-64.

[10] 丁贵立,王奔. 双馈风电机组的非线性变结构功率解耦控制[J]. 中国电力, 2013,46(8): 64-69.

[11] 高为炳. 变结构控制的理论及设计方法[M].北京: 科学出版社,1996．

[12] 刘向向, 李新宇, 王奔,等.变结构控制策略在直驱永磁同步风力发电机中的应用[J].电网技术, 2013, 37(2):520-525.

A Study on the Non-linear Variable Structure Control Strategy for the Low Voltage Ride Through of the Doubly-fed Induction Generator

Gao Lufeng, Wang Ben, Li Xiao, Zhang Rui

(College of Electrical Engineering, Southwest Jiaotong University, Chengdu Sichuan 610031, China)

This paper presents a design method for the low voltage ride through controller of the doubly fed induction generator (DFIG) based on variable structure control of exact linearization. A nonlinear DFIG mathematical model is established in the synchronous rotating dq coordinate system. On that basis, the original nonlinear system model is transformed into a linear system model by means of exact linearization. A DFIG controller for the generator rotor side and the grid side is designed in the principle of variable structure control, and the DC side capacitor voltage is controlled through PI. Finally, a 6×1.5MW DFIG system simulation model is built through MATLAB simulation software. Simulation results show that the designed controller can suppress rotor over-current and DC bus over-voltage after voltage drop, thus realizing low voltage ride through for the DFIG.

doubly-fed induction generator；voltage drop；low voltage ride through； exact linearization；variable structure control

10.3969/j.issn.1000-3886.2017.04.015

TM614

A

1000-3886(2017)04-0052-04

定稿日期: 2017-02-14

高鲁峰(1988-)，男，山东临沂人，硕士生，研究方向为双馈风机低电压穿越，非线性变结构控制。 王奔(1960-)，男，湖南长沙人，教授，博士，研究方向为电力系统非线性和变结构控制。