迪恩涡影响弯管流体运动能量耗散的数值研究

钟 乐， 肖乃玉

(仲恺农业工程学院 轻工食品学院，广东 广州 510225)

迪恩涡影响弯管流体运动能量耗散的数值研究

钟 乐， 肖乃玉*

(仲恺农业工程学院 轻工食品学院，广东 广州 510225)

生态农业设施中存在大量的弯管，无论是气态还是液态物质在弯管中都存在大量的能量消耗，降低能耗是农业节能减排的重要环节之一.在笛卡尔坐标系下，利用数值方法对弯管流动能量耗散进行公式描述.在此基础上以不同几何尺寸的弯管为例，从迪恩涡的影响因素(弯管几何尺寸和离心力)出发对弯管中流体运动的能量耗散进行数值模拟，并得出了能量耗散随迪恩数的变化曲线.为了更精确地描述迪恩涡对能量耗散的影响，借助有限体积法(FVM)模拟管内流场，并采用带旋流修正的realizable k-e双方程模型和SIMPLE算法来求解控制方程组.研究结果表明：r/Rc越大，能量耗散越显著；在层流区和过渡区由离心力所引起的能量耗散相对较低，而在湍流区剧增；迪恩数以5 000为分界点，小于5 000时能量耗散呈一定规律变化，而大于5 000时能量耗散急剧增大.图6，参10.

迪恩涡；能量耗散；弯管；数值方法

近几十年来,农业已成为中国主要消耗能源产业之一.在当前全球能源危机的背景下,如何减少农业生产过程中能源的使用以保持农业未来可持续发展已经成为各国关注的重点和热点问题.随着农业技术的发展,农业结构由传统农业向设施农业转变,设施农业成为农业的重要组成部分,也是高耗能的农业生态系统之一.生态农业设施中存在大量的弯管，无论是气态还是液态物质在弯管中都存在大量的能量消耗，降低能耗是农业节能减排的重要环节.

在曲率效应条件作用下，弯管内存在较大的概率产生迪恩涡.迪恩涡能极大地提高流体的传质和传热性能，但同时也会引起流体的能量耗散，是一种利害兼备的运动.在实际应用中，弯管的能量耗散是必须考虑的重要因素之一.

弯管流体的能量耗散受几何尺寸、流体粘度、主流速度等因素的影响[1,2].Felipe Gallego发现弯管流体能量耗散是由二次流所引起，并且三个方面(管壁粗糙度、弯管曲率和流体温度)进行了实验，结果表明增大管壁粗糙度和弯管曲率能提升立刻能量耗散，流体温度则在一定程度上会影响能量耗散量[3,4]，文献[5]在Boussinesq模型中新引入了能量耗散项.国内也有学者分别就牛顿流体和幂律流体两种情况对圆管内湍流的能量耗散率的计算方法进行了研究和对比[6].

考虑弯管中的迪恩涡及其影响因素，本研究借助数值方法弯管内流体能量耗散的变化规律进行研究，可以在一定程度上减小弯管阻力、降低能耗，对工业应用中弯管的设计有着一定的指导作用.

1 迪恩涡运动及其引起能量耗散的数学描述

迪恩涡在离心力的作用下，弯管中的粘性流体在一定的主流速度下所产生的反向对称涡旋(见图1)[7].

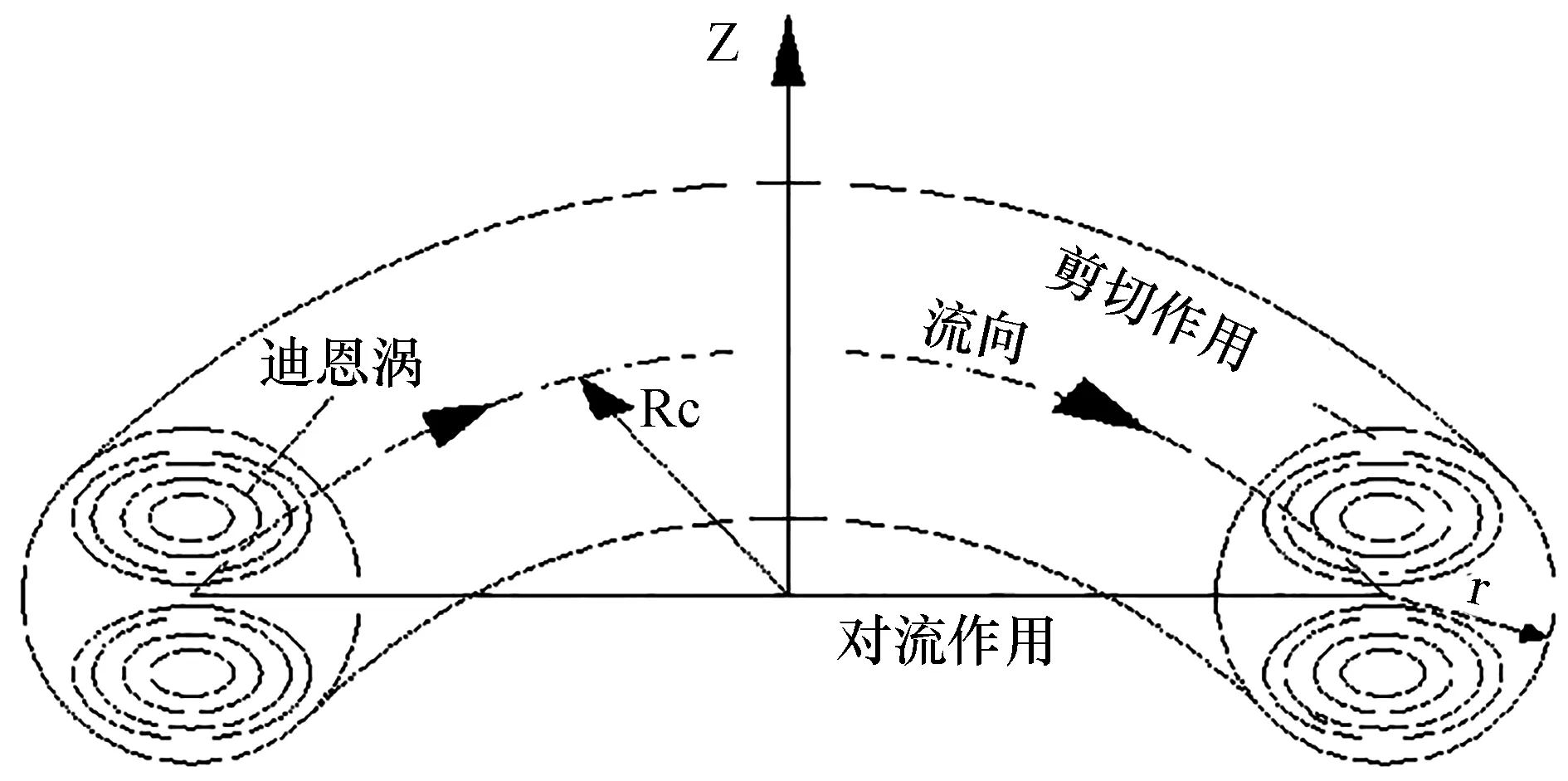
图1 迪恩涡Fig.1 Dean vortex

文献[8]指出迪恩涡对的产生是由于管内流体所受的离心力和粘性力相互作用的结果，在此基础上提出了一无量纲数——迪恩数，通常迪恩数可表示为：

De=Re·(r/Rc)0.5=V·2r·υ-1·(r/Rc)0.5

(1)

由此可看出，迪恩涡主要受到几何尺寸r/Rc、流体粘度υ以及由曲率半径Rc和速度V共同引起的离心力的影响.

假设弯管为圆环的一部分，在笛卡尔坐标系下建立其物理模型(图2).取弯管内任意固定微元体δV，分别从x，y，z三个方向对其进行受力分析，其中x方向上所受表面力可由图2b表示.

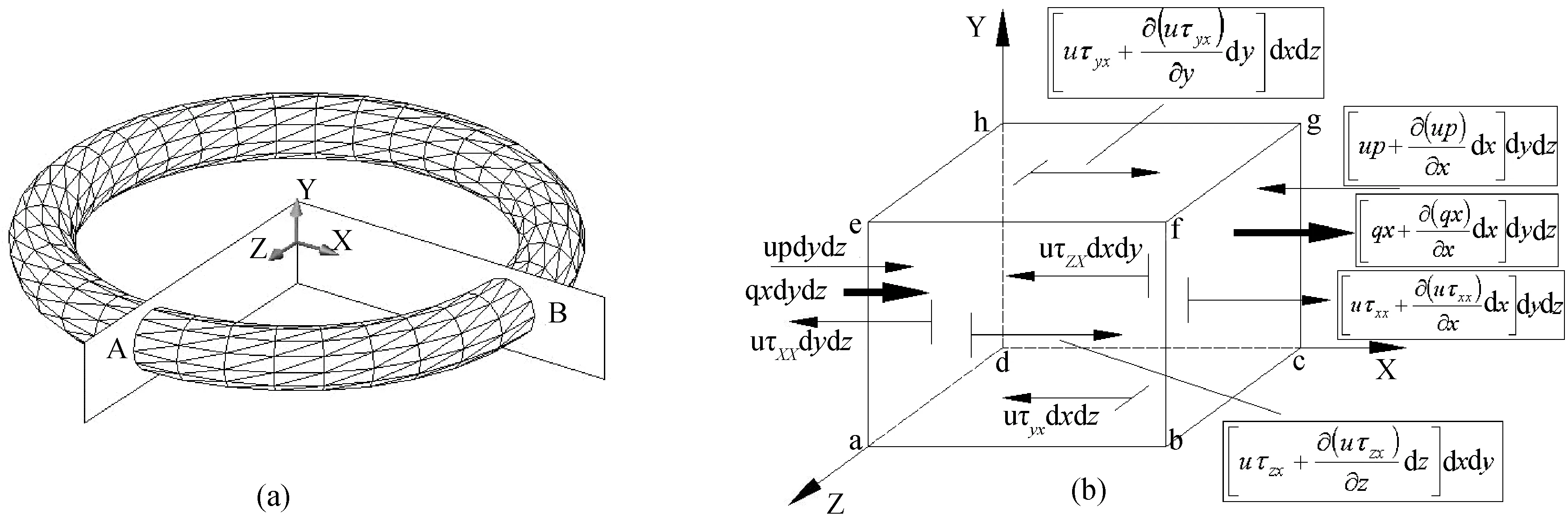
图2 弯管模型(a)及其微元体δV的能耗分析(b)Fig.2 energy consumption analysis of bend model (a) and its micro body Delta V (b)

忽略重力因素的影响，将x方向上的受力分析推广到y，z方向上，得到弯管内迪恩涡运动的能量方程[9]：

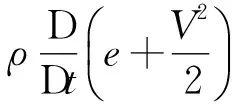
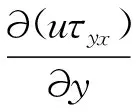
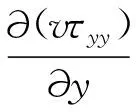
(2)

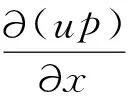
2 迪恩涡引起能量耗散的数值模拟

2.1 控制方程和Realizable k-e模型

迪恩涡为一具有旋流特性的内流运动，对于一定的密度和粘度条件下的不可压缩流体的内流运动，连续性方程(即质量守恒方程)、Navier-Stocks方程(即动量守恒方程)和能量方程共同组成了迪恩涡运动的控制方程.

其中,动量守恒方程可表示为：

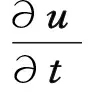
(3)

质量守恒方程表示为：

·u=0

(4)

能量方程如式(2).

式中,D/Dt为物质导数；为Hamilton梯度算子；v为运动粘度；u为速度矢量；2为Laplace算子；P为压力梯度.

考虑到迪恩涡运动的旋流特性，利用标准k-e湍流模型无法得到理想的计算结果.带旋流修正的Realizablek-e模型不仅为湍流粘性增加了一个公式，并且为耗散率增加了新的传输方程.带旋流修正的Realizablek-e方程的湍动能传输方程可表示为：

Gk+Gb-ρε-YM+Sk

(5)

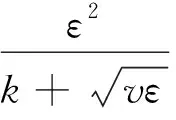
(6)

方程中Gk是由层流速度梯度而产生的湍流动能；Gb是由浮力而产生的湍流动能；C2和C1ε是常量；YM是过渡扩散产生的波动；σk和σε是k方程和e方程的湍流Prandtl数，Sk和Sε为用户自己定义选项.而C1可以通过下式来计算：

(7)

上述模型常量为：C1=1.44，C2=1.9，σk=1.0，σε=1.2.

2.2 模型尺寸及初始条件

根据迪恩涡的影响因素，模拟对象为不同几何尺寸的长600 mm、直径60 mm的弯管(表1)，流体介质选用常温水，在不同的进口速度下进行模拟.层流区(Re≤2500)、过渡区(25001.38×104)各取2个速度值.层流区速度取0.03 m/s、0.05 m/s；过渡区取0.15、0.3 m/s；完全湍流区取0.4、0.9 m/s.

表1 弯管几何参数Tab 1 geometric parameters of bent pipe

2.3 网格和边界条件

采用非结构网格进行网格划分，设置三类边界类型(见图3)：进口采用速度入口边界；管壁为壁面边界；出口采用自由出流边界，并且在靠近管壁面处设置边界层.其中速度入口为“边界法向”方式；指定湍流描述为“水力直径”和“湍流强度”；边界为“无滑移壁面” 和“静止壁面”，粗糙度常数取0.5.借助有限体积法[10]对控制方程组进行离散化并利用SIMPLE算法求解控制方程，在对动量方程和湍流方程进行离散化时，采用一阶迎风格式.

图3 模型的网格划分图(a：截面网格；b-f分别为Rc=477.5mm， 318mm， 239mm， 212mm，159mm时的弯管网格)Fig.3 mesh diagram of model (A:cross section mesh,B-F,Rc=477.5mm,318mm,239mm,212mm,159mm)

3 模拟结果及分析

数值模拟以标准状态下的水为介质，从迪恩涡的影响因素——几何尺寸(r/Rc)和离心力两方面研究能量耗散的变化规律，并综合考虑迪恩涡的影响因素，对能量耗散与迪恩数的关系进行分析.模拟结果如下.

3.1 弯管几何尺寸对能量变化的影响

对于5种不同几何尺寸的弯管，从进口开始每10°取一截面，在不同的进口速度vi下监测各个截面上的平均能量的变化(模拟结果见图4).结果表明：在不同的进口速度条件下，5种弯管截面平均能量均呈降低趋势，并且r/Rc越大，能量降低得越快.此外还发现，流体在层流区运动时(即vi=0.02 m/s和0.04 m/s时)，各截面平均能量变化较平缓；当流体运动到过渡区(vi=0.1 m/s和0.25 m/s)时，对于r/Rc=0.052和0.079的弯管，截面平均能量降低趋势更明显，并且r/Rc=0.079的弯管能量在50°截面附近有突然降低的趋势，而对于r/Rc=0.105，0.118和0.157的弯管，截面平均能量在80°～100°截面上也出现突然降低的现象，但是能量的降低值较小；在完全湍流区(vi=0.3 m/s和0.8 m/s)，截面平均能量降低最快，并且对于r/Rc=0.105，0.118和0.157的弯管，在80°～100°截面上平均能量出现显著的“骤降”现象.

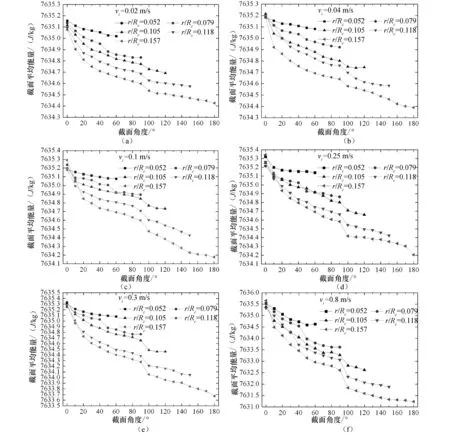
(a：vi=0.02 m/s； b：vi=0.04 m/s； c：vi=0.1 m/s； d：vi=0.25； e：vi=0.3 m/s； f：vi=0.8 m/s)图4 截面平均能量随弯管几何尺寸的变化Fig.4 average energy of section changes with bend geometry

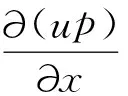
3.2 截面能量耗散量随离心力的变化

(a：r/Rc=0.052； b：r/Rc=0.079； c：r/Rc=0.105； d：r/Rc=0.118； d：r/Rc=0.157)图5 离心力对弯管能量耗散的影响Fig.5 Effect of centrifugal force on energy dissipation of bend pipe

另外，流体处于层流区和过渡区时，由于离心力所引起的能量耗散虽呈升高的趋势，但是总体较平缓而且耗散量相对较低；而当流体处于完全湍流区时，流体运动的能量耗散值陡增.引起这种现象的原因在于，当流体处于层流区和过渡区时，在离心力的作用下，弯管内产生迪恩涡，且此时流体主要运动形式为迪恩涡，能量耗散主要由迪恩涡引起.当流体进入完全湍流区后，迪恩涡开始扭曲变形，并分裂为更小尺度的涡旋甚至是Kolmogorov尺度的微涡旋，最后在粘性力的作用下微涡旋消失，能量转化为热能.湍流引起的能量耗散远大于迪恩涡引起的能量耗散.

3.3 能量耗散值随迪恩数的变化

由式(1)计算不同几何尺寸及进口速度的迪恩数：

表2 不同几何边界及进口速度的迪恩数

Tab 2 Dean numbers at different inlet velocities and geometric boundaries

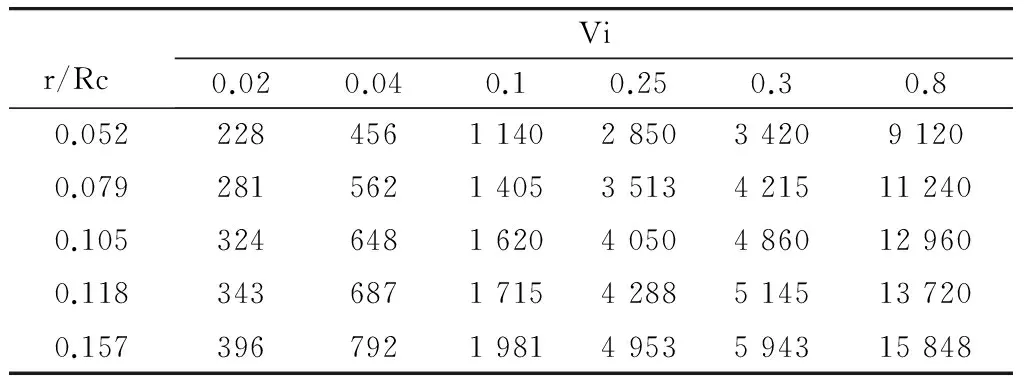
r/Rc Vi0.020.040.10.250.30.80.05222845611402850342091200.079281562140535134215112400.105324648162040504860129600.118343687171542885145137200.15739679219814953594315848

综合以上的结论，得到迪恩数与弯管流动能量耗散的关系(见图6).由图6知，在迪恩数小于5 000附近的某一值时，能量耗散呈近似的周期性变化；当迪恩数大于5 000后，虽然能量耗散出现一定的回落，但是在大于迪恩数大于9 000后，能量耗散持续递增.其原因在于，当迪恩数小于5 000时，流动状态处于层流区或者过渡区，弯管内的流动主要以迪恩涡为主，迪恩涡的周期性运动引起了能量耗散的波动；而在迪恩数大于5 000的范围内，迪恩涡开始扭曲破裂，分裂为小尺度的涡旋，能量耗散程度更剧烈，此时能量耗散值显著增大.

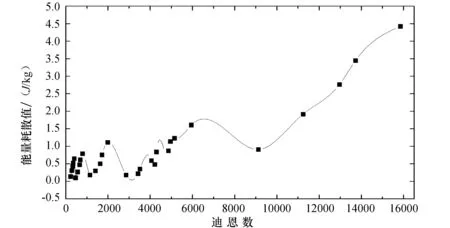
图6 能量耗散随迪恩数的变化Fig.6 the change of energy dissipation with Dean number

4 结 论

在笛卡尔坐标系下对迪恩涡引起能量耗散进行数学描述，并利用数值方法从迪恩涡的影响因素——弯管几何尺寸、离心力两个方面对弯管流动能量耗散的变化规律进行了研究.综合考虑几何尺寸和离心力的影响，分析了能量耗散随迪恩数的变化规律.研究结果表明：

(1)在不同的进口速度条件下，5种不同几何尺寸弯管的截面平均能量呈降低的趋势，并且r/Rc越大，能量降低得越快.并且r/Rc=0.105，0.118和0.157的三种弯管在80°～100°截面上平均能量出现显著的“骤降”现象.

(2)在离心力的作用下弯管的能量耗散均呈降低的趋势，离心力越大，能量耗散值也越大.并且能量耗散在层流区和过渡区较低，在完全湍流区剧增.

(3)在迪恩数小于5 000附近的某一值时，能量耗散呈近似的周期性变化；当迪恩数大于5 000后，虽然能量耗散出现一定的回落，但在大于迪恩数大于9 000后，能量耗散持续递增.

[1] Samy M,Ei-behery,Mofreh H,Hamed,M.A.EI-KADI,et al.CFD prediction of air-solid flow in 180° curved duct.[J]Powder Technology,2009 (191):130-142.

[2] K.A.Ibrahim,M.A.EI-KADI,M.H.HAMED,et al,Effect of bend orientation and flow direction on the behaviour of gas-solid flow,[C] Proc.8th Int.Conf.of Fluid Dynamics and Propulsion,December,2006:14-17.

[3] Felipe Gallego,Subhash N.Shah.Friction pressure correlations for turbulent flow of drag reducing polymer solutions in straight and coiled tubing.[J]Journal of Petroleum Science and Engineering,2009 (65):147-161.

[4] Lamb.H.Hydrodynamics.[M]Dover:NY,USA.1932.

[5] Madsen P A,Sorensen O R,Schaffer H A.Surf zone dynamics simulated by Boussinesq type model.Part 1.Model description and cross-shore motion of regular waves.[J]Coast.Eng.1997,32,255-287.

[6] 张劲军,严大凡.圆管内湍流流动能量耗散率近似算法的可靠性分析.[J]石油大学学报(自然科学版),2002,26(6):82-85.

Zhang Jinjun,Yan Da.Reliability analysis of energy dissipation rate approximation algorithm for turbulent flow in cylindrical tubes.[J] Journal of Petroleum University (NATURAL SCIENCE),2002,26 (6):82-85.

[7] 湛含辉,成 浩,刘建文,等.二次流原理.[M]长沙：中南大学出版社，2006:8-9.

Zhan,Zhan Hui,Cheng Hao,Liu Jianwen,et al.Two principles of flow.[M]:Central South University press,2006:8-9.

[8] W.R.Dean.Note on the motion of fluid in a curved pipe.[J]Philosophical Magazine.1927 (20):208-223.

[9] John D,Anderson,Jr.Computational fluid dynamics:The basic with application.[M] McGraw-Hill Companies,Inc.1995.

[10] Patankar S V.Numerical heat transfer and fluid flow.[M]Hemisphere Publishing Co,New York,1980:11-21.

Abstract：Mathematics descriptions of the energy dissipation of fluid motion in curved pipes were performed under Cartesian Coordinates by means of numerical methods.On the base of the mathematics description,numerical simulation was carried out to study the energy dissipation from the influencing factors of Dean Vortices (geometry size and centrifugal force),and the relationship between Dean Number and energy dissipation was analyzed afterward.During the simulation,the Finite Volume Method,SIMPLE algorithm and realizable k-e equations were adopted to solve the Dean Vortices more precisely.The results showed that the energy dissipation increased with the geometry sizer/Rcand the centrifugal force.And the energy dissipation varied according to certain rules before the Dean number reached 5 000,while increased significantly when Dean numbers were larger than 5 000.6figs.,10refs.

Keywords：dean vortices;energy dissipation;curved pipe; numerical simulation

Biography：Zhong Le ,male,born in 1984,master,lecturer,research direction:environmental engineering.

NumericalsimulationofEnergydissipationbyDeanVorticesincurvedpipes

ZHONGLe，XIAONai-yu*

(Zhongkai University of Agriculture and Engineering,Guangzhou 510225,China)

TB126

A

2017-05-22

国家自然科学基金项目(编号：51403245)、广东省教育厅育苗项目 (编号：KKA13412Q)

钟 乐(1984-)，男，江西宜春人，硕士，讲师,研究方向：环境工程.

*通讯作者：lionel_Z@126.com

10.3969/j.issn.2095-7300.2017.03-034