基于车联网的轻型汽油车排放估计

胡 杰，曾德昌，孙自圆，韦天文，黎业辉

（1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070；2.上汽通用五菱汽车股份有限公司，广西 柳州 545000；3.汽车零部件技术湖北省协同创新中心，湖北 武汉 430070）

基于车联网的轻型汽油车排放估计

胡 杰1，曾德昌1，孙自圆2，韦天文2，黎业辉3

（1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070；2.上汽通用五菱汽车股份有限公司，广西 柳州 545000；3.汽车零部件技术湖北省协同创新中心，湖北 武汉 430070）

针对目前汽油车排放无法实施有效远程监控的问题，提出了一种基于车联网的汽油车排放估计方法。选用径向基神经网络作为排放估计模型建立的基础，以速度、加速度和发动机功率作为模型的输入量，以不同工况的仿真数据为训练样本，采用资源分配网络算法（RAN）确定隐层节点数，通过剪枝策略简化网络，以改进的粒子群算法（MPSO）对网络参数进行全局最优搜索优化模型。结合自主研发的车辆信息远程采集系统实现远程数据采集，将远程采集的状态数据导入排放估计模型实现远程排放估计。最后，通过车辆实际道路排放测试实验，将排放估计模型输出结果实验数据对比分析，验证了该排放估计方法的有效性。

车联网；RBF神经网络；排放估计

1 前言

随着我国汽车保有量的迅速增长，汽车尾气排放物对环境造成的污染问题日益严重。为此，相关政府部门不断制定越来越严格的排放法规。如国家检测单位对汽车的尾气排放水平进行实验认证，新车强制要求搭OBD-II系统。但排放认证实验并不能完全反映汽车在实际道路上行驶时的真实排放水平，同时OBD-II系统对于汽车在实际使用中的排放水平缺乏有效监管。因此，需要一种更为准确有效的途径实现车辆实时道路的排放估计。

目前，国内外的研究人员对此做了大量研究。发达国家对车辆排放模型的研究以美国为代表，经历了从传统的MOBILE模型到比较适合现代交通情况的CMEM，MOBILE用FORTRAN语言编写，能够估计在平均用车时的排放因子CO、HC、NOX，该模型主要表达为平均速度的函数，对如加速、怠速、急减速过程不敏感，不能代表车辆实时道路的排放情况。CMEM以大量车型的瞬时排放数据为研究基础，考虑了车辆排放潜在影响因素，对排放估计较为准确，但此方法需要大量数据和繁琐的实验支持，对模型参数的高精度要求和对数据量的过高要求使模型难以建立。董刚，陈达良考虑瞬态车速和加速度的影响，利用回归分析的方法对HC、CO、NOX的排放因子进行估算得到的模型准确性较高，但难以处理复杂的输入参数，不利于实际应用[1]。刘玉长、李君[2]建立了基于RBF神经网络的汽油机稳态排放模型，辨识效果较好，但无法对动态过程进行辨识。

由此可知，国内对于排放模型的研究集中于实验室以及排放因子模型的研究，没有基于实时道路的排放估计研究。本文提出了一种基于车联网的轻型汽油机排放估计方案。

2 基于RBF神经网络排放估计模型的建立

考虑到尾气排放数据随着速度和加速度的变化呈严重的非线性振动变化；排放估计模型需要应用到汽车实际道路行驶过程中的尾气排放监测，需要一个快速的预测模型来计算出尾气排放数据。本文以RBF径向基神经网络为基础，仿真数据为样本，构建排放估计模型，并通过剪枝策略和改进的粒子群算法（MPSO）优化模型。

2.1 确定模型输入/输出量

汽车运行状态是影响其尾气排放情况的主要因素之一，通常是以汽车运行状态和尾气排放水平之间的关系建立机动车微观排放模型。作为模型的输入，汽车运行状态的准确表示在很大程度上决定了模型的有效性。汽车运行状态受到驾驶行为、交通状态等因素影响而呈现出复杂多变[3]，不能仅仅依靠汽车速度、加速度来表示汽车运行状态。

本文采用ADVISOR仿真软件建立仿真模型，实验车型为某MPV车型，汽车主要性能参数见表1。

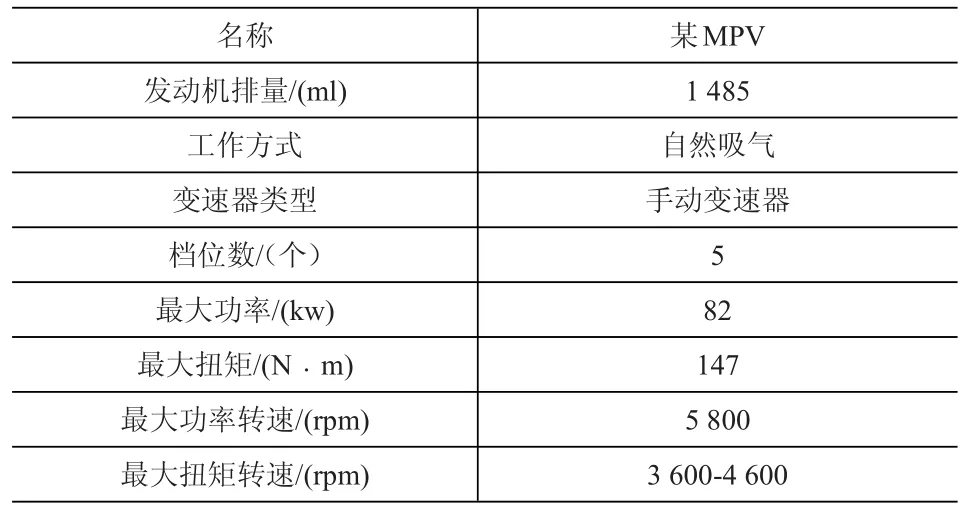
表1 汽车主要性能参数

以汽车性能参数为依据，在ADVISOR软件中建立仿真模型。对汽车初始状态、行驶循环、路面坡度等参数进行设置。合理改变行驶循环以便仿真汽车的不同工况，如怠速、加速、减速和匀速，同时软件可以通过Interactive Simulation功能实现实际驾驶汽车仿真。模型建立完成后，运行不同工况或状态仿真模型可得到相应的仿真数据，该数据可作为分析排放影响因素的理论依据和排放估计模型的训练样本。

通过改变行驶循环和控制变量法可分别得到行驶工况、速度、加速度、载重和路面坡度五个主要因素与排放物（HC、CO、NOX）的关系数据。通过对数据的处理得到关系曲线，对其定性分析。考虑到现有的排放估计模型多以速度和加速度作为估计模型的输入参数。但当汽车以相同的速度、加速度在不同坡度的道路上行驶，其尾气污染物排放率明显是不同的，不同的载重量也类似，所以还需考虑发动机的输出功率。因此，可以总结为速度、加速度和发动机功率三个因素。

2.2 排放估计模型建立

由于不同物理量之间数值相差悬殊，达到多个数量级上的差异。为了避免同一维中较大数据因数值差异过大对较小数据的支配作用，防止因各维数据之间差异过大影响模型的预测效果，同时也为了加快训练速度，在建模之前需要对训练集和测试集样本进行归一化处理。

2.2.1 确定隐含节点个数。RBF神经网络的隐层节点个数对网络的泛化能力起着决定性作用。隐层节点个数过多会造成网络结构过度冗余，将会导致在网络训练和测试时需要消耗大量的软硬件资源，而且容易导致网络出现过拟合的现象；隐层节点个数过少，导致网络结构太小，不足以将所描述的问题表达清楚，造成部分关键信息丢失。

本文采用了资源分配网络算法（RAN），根据“新颖性”条件来选择隐层节点。

设样本数据集A(j)={(xj,yj),j=1,2,…,n}，开始时由于网络还没有隐层节点，需要初始化网络参数，本文利用第一、第二组样本数据(x1,y1)和(x2,y2)进行初始化：

w0=y1,w1=y2-y1,c1=x2,σ1=μδ2max（1）

其中0＜μ＜1，δmax为输入样本，xj之间的最大距离。

其中，ek为误差，ε为期望的精度，cnearest为距离xj最近的隐层节点中心，δj=max{γδmax,δmin}，γ∈(0,1)，δmax和δmin分别为输入空间xj之间的最大和最小误差。

如果上述式（2）或者式（3）任一不满足，则不增加隐层节点；否则增加一个隐层节点，并将该节点的参数设置为：

wL+1=ek,cL+1=xj,σL+1= γdj（4）

在选择隐层节点时，虽然得到的隐层节点满足式（2）和式（3），但其中往往还存在一些对网络输出贡献不大的节点，它们的存在有可能会导致所构造的网络变得冗余。所以还需要对隐层节点作进一步的筛选，本文采用剪枝策略来删除不必要的节点，从而对网络的结构起到简化的作用。具体步骤如下：

（1）对于每次的输入输出的(xn,yn)，隐层节点的输出为：

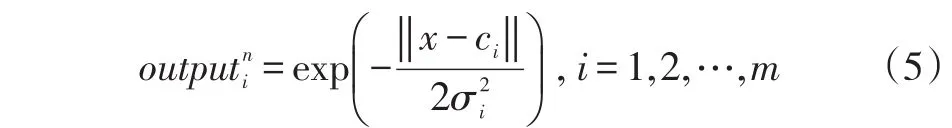
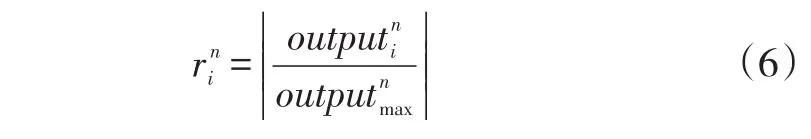
2.2.2 寻找网络参数最优解。本文使用改进粒子群算法求解网络参数的最优解。基本粒子群算法（BPSO）是一种基于迭代模式的优化方法。在该算法中，当搜索最优解的过程进行到后期时，粒子群的种群多样性会逐渐降低，容易陷入局部最优的状态。所以如何实现粒子种群在寻优的后期保持一定的多样性将是优化基本粒子群算法的关键。本文对粒子群算法提出如下改进，形成改进粒子群算法（MPSO）：

①对加速常数和惯性权值进行动态自适应改变，随着迭代次数的增加，加速常数c1从初始值c1max非线性减小至c1min，相反c2从初始值c2min非线性增加至c2max。过程如下：

其中，Maxlter为最大迭代次数，lter为当前迭代次数，α,β∈{0.5,1,1.5,2.0}。

为了让粒子群在后期能够收敛到全局最优，必须阻止粒子群在前期就已经陷入局部最优。通过以上改进，粒子速度更新公式中的加速常数和惯性权值将会进行动态改变，表现为粒子的飞行速度和飞行方向更加多变，这样便使得粒子群在前期能够在全局空间内飞行搜索，保证了在后期收敛到全局最优的可能性。

②在寻优的后期增加种群的多样性，由于对后期的概念并没有一个准确的定义，也没有判断种群多样性的明确标准。本文采用通过进化停滞步数来判断增加种群多样性的时机。首先确定停滞步数的阈值T，一般取值范围为4-7，当进化停滞步数超过了阈值的时候，对种群进行变异，产生一组变异粒子。保持原速度更新公式不变，但是位置更新如式（10）：

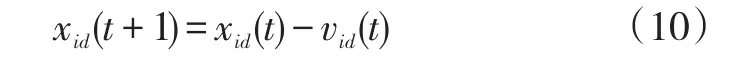
变异粒子将会沿着pg的反方向飞行，其余粒子按原公式更新其位置和速度，向着pg飞行。这样种群的多样性就可以得到提高，从而防止陷入局部最优。种群数量与变异率的乘积即可以得到变异粒子的数量，变异率一般取0.3-0.6，T的取值范围为4-7。

利用前文所述的改进粒子群算法求解网络参数的最优解，具体步骤如下：

①初始化粒子群的参数。以基函数的中心c、基函数的方差σ、隐含层到输出层的连接权值ω为粒子的参数编码，并在一定范围内产生粒子的速度vi和位置xi的一个随机值作为初始值。进化代数t取初始值为1。

②按归一化均方根误差的形式计算各个粒子的适应度，计算公式如下：

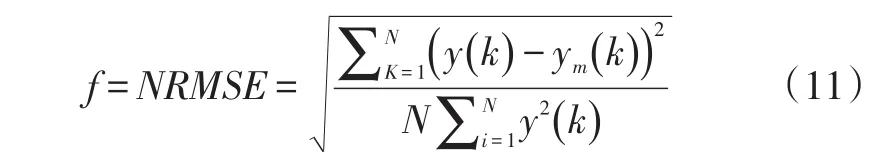
③对于每一个粒子，利用式（11）计算得到适应度后，与其pi所对应的适应度进行比较，若更好则更新pi。

④对于每一个粒子，得到对应的pi后，对比pi和全局最优pg对应的适应度，若更好则更新pg。

⑤结合基本粒子群算法与公式（7）-（9），不断改变粒子的速度vi和位置xi，同时对加速常数和惯性权值进行动态自适应改变。

⑥若T代的最优值没有明显变化，则开始对粒子群进行变异，按照变异率选取一定数量的变异粒子，变异粒子的位置按式（10）进行更新，变异粒子的速度以及其余粒子的位置与速度均按照步骤⑤更新。

⑦判断是否结束寻优过程，判断条件与其他迭代模式算法一样是最大迭代次数或者目标精度。若条件符合，则结束寻优过程，得到网络参数的最优解；否则当前代数增加1，并转向步骤④继续进行迭代。

2.2.3 模型建立。利用仿真分析得到的数据，得到3 353个样本，考虑到短时实际工况，形成(3 353-m)个样本，m取初值为5。所有输入向量组成(m+3)*(3 353-m)维的输入矩阵，所有输出向量为3*(3 353-m)维的输出矩阵。通过randperm()函数将1到(3 353-m)的顺序数列随机打乱，得到数列randnum数列，再由此取1 100个训练样本、1 100个测试样本和500个监视样本。

建立模型过程中用到的重要参数设置如下：RAN中 ε=0.01，γ=0.9，μ=0.6，MPSO中 m=40，α=β=2.0，γ=1.5，c1max=c2max=2.5，c1min=c2min=0.5，ωmax=0.9，ωmin=0.4。

本文对比了利用不同短时实际工况作为模型输入的预测结果均方根误差，见表2。最终决定选取工况点前3s内的速度以及工况点的速度为短时实际工况，即m=3。这也与其他研究中对加减速工况的普遍定义相符合，即加速度或减速度连续3s均大于0.45m/s2则认为是加速工况或减速工况。为了表示汽车行驶工况，并不是m取值越大越好。因为汽车在城市中行驶时，大多数情况持续加速一般在4s以内，当m=4时，短时实际工况已经考虑了5s内的速度情况，可能不能准确表征汽车运行状况，对模型来说会造成干扰。

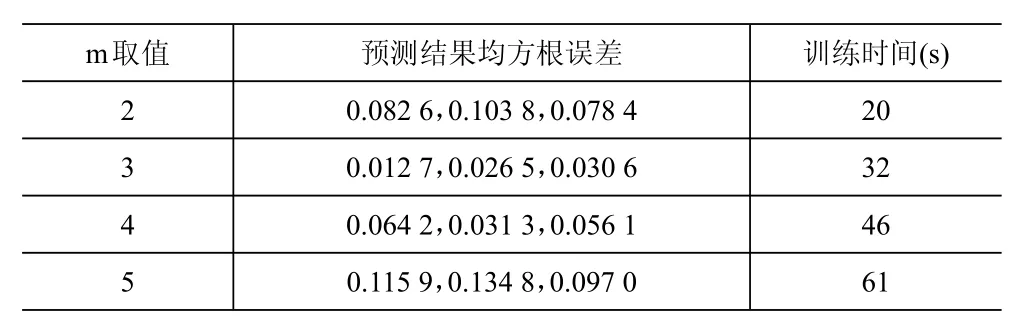
表2 模型预测结果均方根误差对比表

2.3 排放估计模型测试

利用ranperm()函数在仿真数据中随机选取1 100个样本点，经过本排放估计模型的计算得到对应的预测值，根据仿真数据中对应的实际值得到均方根误差，各污染物排放率预测值均方根误差分别见表3：

表3 各污染物排放率预测值均方根误差

为了更直观地展示测试样本预测值与实际值的拟合效果，将模型输出结果与样本实际值绘于同一张图中，并将各个样本点按排放率大小进行排序，同时采用了主次纵轴，较大预测值与较大实际值对应次纵轴，以图1-图3分别对应HC、CO、NOx三种污染物的排放率预测结果。三种污染物的预测值均方根误差均小于5%，预测效果良好。

同时还将本算法与MATLAB的神经网络工具箱newrb()建立的近似(approximate)径向基神经网络以及通过基本粒子群算法（BPSO）优化的径向基神经网络进行对比，见表4。

从对比结果来看，本文通过运用RAN算法和MPSO算法使得RBF神经网络结构得到了较大的优化效果，仅通过使用23个隐层节点和34次迭代就在一定程度上降低了各项误差指标，训练时间也大幅下降。

图1 HC排放率预测效果

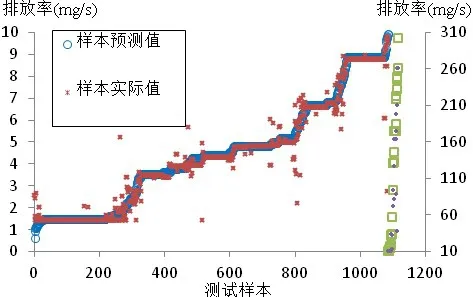
图2 CO排放率预测效果

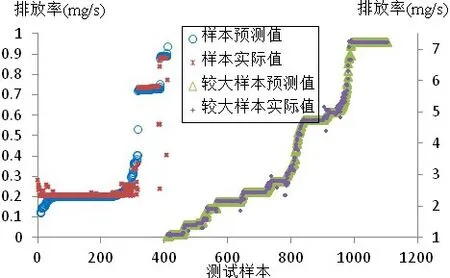
图3 NOx排放率预测效果

表4 三个网络性能比较

3 汽车实际道路排放测试实验

采用基于车联网的车辆运行状态信息采集系统和基于RBF神经网络的排放估计模型，通过实车在实际道路的排放测试实验来验证该信息采集系统和排放估计模型的可行性。

3.1 实验方案

本实验采用对比实验的方法。使用课题组自主研发的车载终端实时采集汽车运行数据，车载终端硬件部分包括微处理器芯片（MCU）、CAN收发器、2G模块、GPS模块、电源模块、启动检测模块。其硬件实物如图4所示。使用SEMTECH-DS车载排放分析仪来进行实际道路车辆尾气污染物排放率测试，实物如图5所示。在实验路线的选择上，为了采集到车辆在不同行驶工况下的排放数据，实验路线应包含城市路段、快速路段和高速路段。

图4 车载终端

图5 SEMTECH-DS车载排放分析仪车内布置图

实验过程中，SEMTECH-DS车载排放分析仪以1Hz的频率实时测量汽车尾气中NO、NO2、THC、CO、CO2和O2的质量浓度，SENSOR Tech-PC软件结合EFM流量计的实时数据计算出尾气各成分的质量排放率，同时排放分析仪以相同的频率OBD接口请求车辆状态信息数据。车载终端通过OBD接口与车辆CAN总线通信，以1Hz的频率向该模块发送标准CAN帧来请求车辆状态信息数据，然后接收该模块返回的带有所需信息数据的标准CAN帧。最后车载终端通过移动互联网将这些原始数据实时发送至后台服务器，将服务器获取的车辆状态信息导入排放估计模型，得到排放估计值。由于本课题需要分析这两方面数据之间的关系，所以必须保证两方面数据在时间上严格同步，这就需要在实验之前将笔记本电脑和服务器进行时间同步。

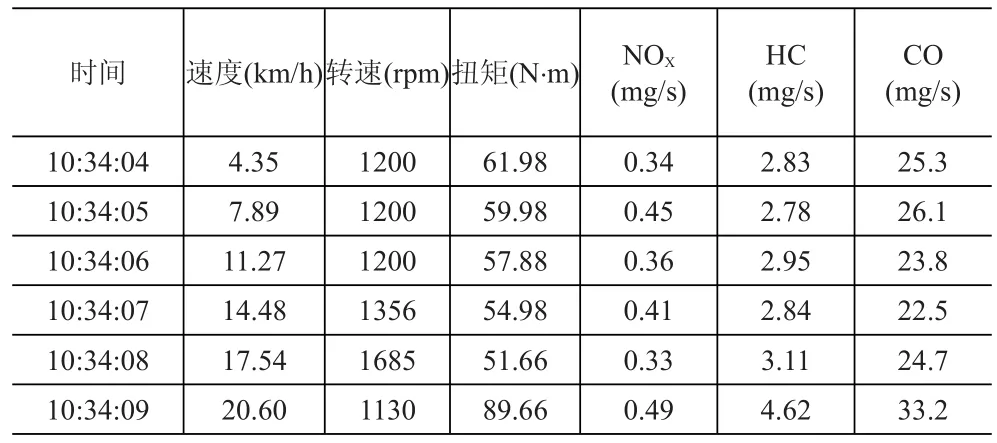
表5 实验数据表

通过比较排放仪采集的车辆状态信息和车载终端采集的车辆状态信息，验证基于车联网的数据采集系统的可行性；通过比较排放仪检测的排放值和排放估计模型的排放值，验证排放估计模型的可靠性。

3.2 实验结果及分析

从服务器调出实验车辆在实验过程中上传的车辆状态信息数据，并按照本文提出的短时实际工况进行整理，共5426组有效数据，部分数据见表5。

利用前文所述建模方法，选取1 000组实验数据作为训练集，建立模型过程中用到的重要参数如下设置：RAN中 ε=0.01，γ=0.9，μ=0.6，MPSO中 m=40，α=β=2.0，γ=1.5，c1max=c2max=2.5，c1min=c2min=0.5，ωmax=0.9，ωmin=0.4。选取800组实验数据对所建立的模型进行测试，预测效果达到了第2节中模型的预测水平。具体见表6。

表6 各污染物排放率预测值均方根误差

图6至图8为各污染物排放率预测效果图。可以观察到，预测效果良好，对各范围内的排放率，预测值与实际值吻合程度较高，基本保持在实际值上下一定范围内波动。

预测结果相比第2节中的模型预测效果有所降低，

原因可能是：

图6 HC排放率预测效果

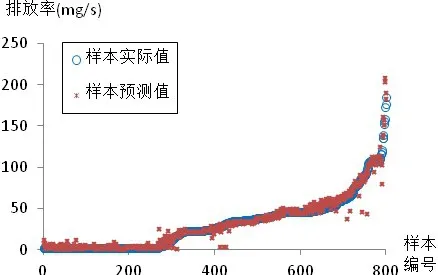
图7 CO排放率预测效果图

图8 NOx排放率预测效果

①实际实验的数据相比仿真所得数据更复杂，仿真分析中采用的循环是ADVISOR自带的标准工况循环，车辆速度等参数基本按照循环准确改变，而实际实验中车辆行驶在实际道路上，驾驶员对车辆的控制相当复杂且不稳定，波动范围因人而异。

②由于发动机排气到采样管这个过程需要一段时间，排放分析仪采集的尾气样本可能是发动机在前一个不确定时刻运行产生的废气。加之车联网信息采集系统得到的数据与实际存在一个微小时间差，车辆运行状态数据与车辆尾气污染物排放数据的对应关系欠缺更精细的考虑。

4 结束语

本文通过理论分析，确定了轻型汽油车在实际道路行驶过程中影响排放水平的关键因素，建立了由转速、加速度和功率3个参数为输入的RBF神经网络排放估计模型。基于车联网开发车辆信息采集系统，将排放估计模型和车辆信息采集系统相结合实现远程排放估计。经验证，车辆信息采集系统运行稳定，能够采集到准确的车辆运行信息，所建模型能够较准确地估计轻型汽油机的实时排放率。同时所建立估计模型在精度上略有不足。若要提高模型精度和模型对工况的适应性，还应考虑其他影响因素，如发动机冷却液温度、大气温度、发动机老化程度等。

[1]夏韡.城市道路轻型车微观排放模型研究[D].长春:吉林大学,2005.

[2]刘玉长,李君.基于人工神经网络的汽油机稳态排放模型辨识[J].现代车用动力,2009,(2):32-35.

[3]周斌.基于BP神经网络的内燃机排放性能建模与应用研究[D].成都:西南交通大学,2004.

[4]李骏.汽车发动机节能减排先进技术[M].北京:北京理工大学出版社,2011.

[5]陈军辉,范武波,钱骏,等.利用IVE模型建立成都市轻型汽油客车排放清单[J].环境科学学报,2015,35(7).

[6]田灵娣,樊守彬,张东旭,等.行驶速度对机动车尾气排放的影响[J].环境工程学报,2016,10(11):6 541-6 548.

[7]Chen M,Xu Z,Winberger K Q,Sha F.Marginalized denoising autoencoders for domain adaptation[A].The International Conference on Machine Learning[C].Edinburgh,UK,2012.

[8]祁凯.面向车联网的车载故障诊断系统的设计与实现[D].杭州:浙江工业大学,2015.

[9]张辉,柴毅.一种改进的RBF神经网络参数优化方法[J].计算机工程与应用,2012,48(20):146-149.

[10]Jie Hu,Yehui Li,Jun Cai,et al.The Driving Behavior Data Acquisition and Identification Based on Vehicle Bus[A].SAE-TONGJI 2016 Driving Technology of Intelligent Vehicle Symposium[C].2016.

Estimation of Emissions of Light-duty Gasoline Vehicles Based on Internet of Vehicles

Hu Jie1,Zeng Dechang1,Sun Ziyuan2,Wei Tianwen2,Li Yehui3
(1.Hubei Key Laboratory for Modern Automobile Spare Parts&Technology at Wuhan University of Technology,Wuhan 430070;2.SGMW Co.,Ltd.,Liuzhou 545000;3.Hubei Collaborative Innovation Center for Automobile Spare Parts&Technology,Wuhan 430070,China)

In this paper,in view of the unavailability of effective remote monitoring over the gas emissions of gasoline vehicles,we proposed a gasoline vehicle emissions estimation method based on the Internet of Vehicles.Selecting the RBFNN as basis,speed,acceleration and motor power as input,and simulation data under different working conditions as training sample,we used the RAN to determine the number of nodes on the implicit strata,reduced the network using the pruning strategy and carried out the global optimization over the network parameters using MPSO.At the end,by comparing the simulation outcome with the empirical data,we demonstrated the validity of the estimation method.

Internet of Vehicles;RBFNN;emissions estimation

F253.9;F407.471

A

1005-152X(2017)09-0160-07

10.3969/j.issn.1005-152X.2017.09.037

2017-08-05

柳州市科学研究与技术开发计划项目（2016B050101）

胡杰，男，博士，武汉理工大学汽车工程学院副教授，研究方向：发动机电子电控、汽车智能网联技术等；曾德昌，通讯作者，男，硕士研究生，研究方向：汽车智能网联技术、汽车诊断及其应用等。