基于最小二乘支持向量机的黏着状态辨识
刘林凡,何 静
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
基于最小二乘支持向量机的黏着状态辨识
刘林凡,何 静
(湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
针对重载机车黏着状态辨识中分类准确率不高的问题,提出采用布谷鸟遗传算法对最小二乘支持向量机的参数进行优化,并采用交叉验证原理提高该模型的整体泛化性能。首先,采用布谷鸟算法寻找惩罚因子和核参数的初始值;然后,采用遗传算法对最小二乘支持向量机进行训练,从而得到具有最佳参数的最小二乘支持向量机的分类模型。该分类模型将重载机车黏着状态分为正常、故障征兆、微小故障和严重故障4个状态。实验结果表明,提出的最小二乘支持向量机模型在黏着状态辨识中的分类准确率高达94.59%,高于极限学习机的分类准确率(84.61%),证明布谷鸟遗传算法能够有效提高最小二乘支持向量机的分类准确率。
最小二乘支持向量机;布谷鸟遗传算法;重载机车;黏着状态;准确率
1 研究背景
重载机车是实现中长距离大宗货物运输的最佳途径,在实际应用中由于道岔、局部轨面油污、线路不平整等因素,往往出现轮轨黏着状况瞬间恶化的情形。此时,由于轮轨黏着特性的突变,使轮轨间黏着被破坏,机车往往会出现空转或滑行。及时辨识机车的黏着状态,可以防止重大事故的发生[1]。机车复杂作业环境的特点造成辨识黏着状态的难度较高,给黏着状态辨识带来了困难。
近年来,卡尔曼滤波器、人工神经网络和支持向量机等人工智能方法被引入机车黏着状态的研究。文献[2]提出一种基于多速率扩展卡尔曼滤波器的状态识别方法用于检测机车打滑,但提出的检测量仅限于电气量,虽然该方法缩短了检测时间,但检测样本存在局限。文献[3]提出采用神经网络解决机车空气制动过程中的黏着性能优化问题,但神经网络存在收敛速度慢、易产生震荡、易陷入局部最优等问题。文献[4]提出基于二分类支持向量机的高速列车车轮空转预测方法。多分类最小二乘支持向量机的分类性能较好,现已被应用在多个领域。然而,多分类最小二乘支持向量机(least square support vector machine,LS-SVM)在重载机车黏着状态辨识的应用,尚未见公开的文献报道。
根据机车黏着状态采集数据具有小样本的特点,且机车黏着系数和蠕滑速度的关系呈现高度非线性[5],本文提出采用布谷鸟遗传算法最小二乘支持向量机(cuckoo genetic algorithm least square support vector machine,CS-GA-LS-SVM)模型对重载机车黏着状态进行辨识。分类模型将机车黏着状态分为正常、故障征兆、微小故障和严重故障4个状态。通过布谷鸟遗传算法(cuckoo genetic algorithm,CSGA)优化最小二乘支持向量机的惩罚因子和核参数,利用交叉验证方法提高分类模型的整体泛化性能。通过实验,将该算法与基于遗传算法的支持向量机(genetic algorithm support vector machine,GASVM)以及极限学习机(extreme learning machine,ELM)进行比较,以验证本文所提出方法对重载机车黏着状态辨识的有效性。
2 系统描述
在机车轴重的作用下,轮轨接触部位发生弹性形变,形成椭圆形接触区,接触区分为黏着区和滑动区。由于黏着区的相对速度为零,滑动区相对速度不为零产生了蠕滑速度,其大小用蠕滑速度表示:

式中:vs为蠕滑速度;
vd为轮对速度;
vt为列车前进速度。
蠕滑速度的大小决定轮轨间的切向力大小。通常定义黏着牵引力和垂向荷重之比为黏着系数[6],其公式如式(2)所示:

式中:F为机车牵引力,N;
W为轴重,kg;
g为重力加速度,m/s2。
文献[7]提出了黏着系数的经验计算公式,即
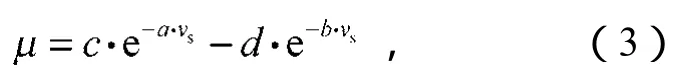
式中a,b,c,d为相关计算参数。
图1为黏着特性曲线。

图1 黏着特性曲线Fig. 1 Adhesion characteristic curve
如图1所示,图中给出了通过大量实验获得的蠕滑速度和黏着系数的经验曲线,也就是黏着特性曲线。黏着特性曲线存在最大黏着系数μmax以及与其对应的最优蠕滑速度vopt。峰值点左右两侧区域分别称为重载机车运行的稳定区域和非稳定区域,在黏着特性曲线的稳定区(安全区)和非稳定区(非安全区)机车车轮状态分别称作车轮蠕滑状态和车轮故障状态,课题组提出将机车黏着状态分为正常、故障征兆、微小故障和严重故障4个状态。运用最小二乘支持向量机进行黏着状态辨识就是利用离线训练得到的最小二乘支持向量机模型,然后利用该模型在线区分当前机车黏着状态。
3 最小二乘支持向量机
将黏着系数μ和蠕滑速度vs作为最小二乘支持向量机模型的输入量xi,黏着状态标签{1,2,3,4}作为模型的输出量yi,因此训练样本集为,i=1, 2, …,n,n为样本数。d维空间中分类决策函数为
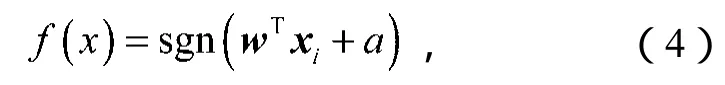
式中:w为权值向量;
a为偏置。
最小二乘支持向量机非线性分类模型可通过求解优化函数[8]来表示:
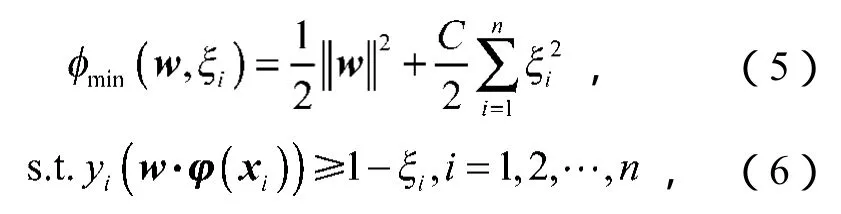
式中:ξi为松弛变量;
C为惩罚因子;
φ(xi)为将数据集映射到高维空间的非线性映射。
则最小二乘支持向量机的分类决策函数为
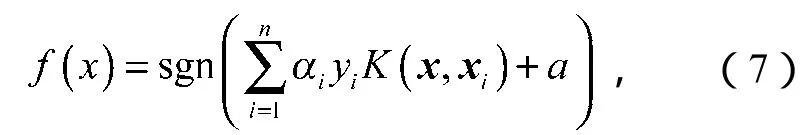
式中:x为样本;
αi为Lagrange乘子;
K为核函数。
本文采用最小输出编码方法实现最小二乘支持向量机多分类。目前在工程实践中,SVM常用的核函数种类主要有如下4种[9]。

以上各式中δ、r和d为核参数。
4 布谷鸟遗传算法
4.1 布谷鸟算法概述
布谷鸟搜索算法(cuckoo search,CS)也被称作杜鹃算法,是基于布谷鸟种群自身所具有的寄生繁衍策略发展而来的一种智能算法。
CS使用的是随机性较强的Levy飞行的搜索方式。Levy飞行是一种随机游走模式,它的步长服从Levy分布,常用的简化[10]表示为
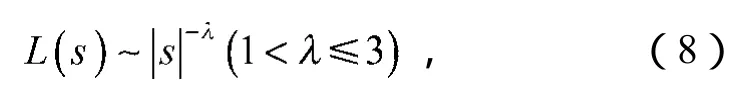
式中:s为步长;
L(s)为步长为s时的概率;
λ为幂次数。
设第i鸟巢在第t代鸟巢位置是,随机搜索路径采用的概率函数为Levy(λ),则布谷鸟寻找鸟巢的路径和位置的更新公式[11]为
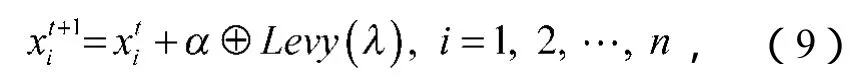
式中:α为步长控制;
位置更新后,随机产生一个[0 1]的数r1,如果r1>Pa(Pa为鸟巢中外来卵被发现的概率),鸟巢位置发生改变;反之则不变,最后保留效果最好的一组鸟巢位置。
4.2 布谷鸟遗传算法
CS-GA-LS-SVM包含了两个步骤:首先,利用布谷鸟算法来寻找最小二乘支持向量机的惩罚因子和核参数较优的初值;然后,利用遗传算法继续对最小二乘支持向量机进行训练,寻找最小二乘支持向量机的最优参数。
CS-GA-LS-SVM算法的流程如图2所示。
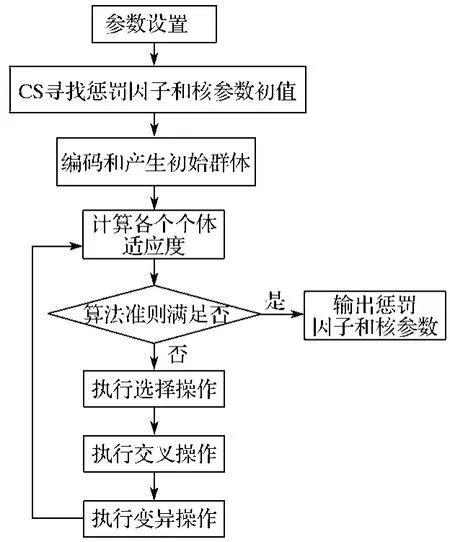
图2 CS-GA-LS-SVM流程图Fig. 2 CS-GA-LS-SVM fl ow chart
4.3 基于CS-GA-LS-SVM模型的分类步骤
采用最小二乘支持向量机分类方法与CS-GA相结合的重载机车黏着状态识别步骤如下。
1)数据样本归一化。由于采集到的重载机车数据样本中各变量差异较大,在建立LS-SVM分类模型前对训练集和预测集样本归一化到[0, 1]区间,计算公式[12]为
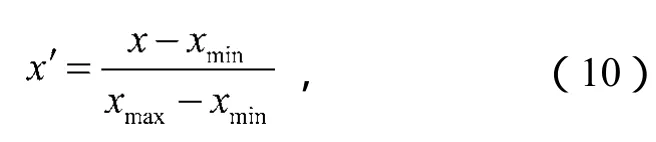
式中:x、x′分别为归一化前、后的值;
xmax为样本最大值;
xmin为样本最小值。
2)CS-GA寻优LS-SVM参数。将训练集样本作为控制量仿真,参数初始化后用布谷鸟搜索算法寻找惩罚因子和核参数初值;进行二进制编码并创建初始种群,适应度定标,进行选择、交叉、变异操作,判断是否满足终止精度或当前迭代次数是否等于最大迭代次数,若满足则解码输出惩罚因子C和核参数δ,否则重新进行遗传操作。
3)建立LS-SVM模型及分类。根据第(2)步得到最佳参数,采用最佳参数训练LS-SVM分类模型,把训练集得到的模型对测试集样本进行分类,并对数据反归一化处理。
4)评价分类模型性能指标分类准确率和耗时,如不符合要求则转至第(2)步,重新寻找惩罚因子C和核参数δ。
5)比较真实值和预测值,得到模型对应的分类准确率。
5 结果对比与分析
课题组提出CS-GA-LS-SVM并实现了此方法,为验证该方法的有效性,搜集了重载机车黏着状态数据集,剔除冗余样本和一些奇异数值数据后,最终选择了300组数据进行研究。分别采用不同的核函数得到的分类准确率如表1所示。

表1 不同核函数的分类准确率对比Table 1 Classi fi cation accuracy comparison of different kernel functions
表1的准确率结果表明,采用高斯径向基核函数在重载机车黏着状态辨识中,分类准确率最高,因此课题组采用此核函数。
5.1 布谷鸟遗传算法的最小二乘支持向量机
在解决重载机车黏着状态辨识的问题中,采用高斯径向基核的LS-SVM模型有2个参数(即δ和C)需要进行优化。课题组提出采用布谷鸟遗传算法来进行此优化工作,并且将其应用于机车的黏着状态识别。最后将CS-GA-LS-SVM多分类结果与GA-SVM和ELM多分类结果进行比较。CS-GA寻参的适应度曲线和测试集分类结果如图3~4及表2所示。
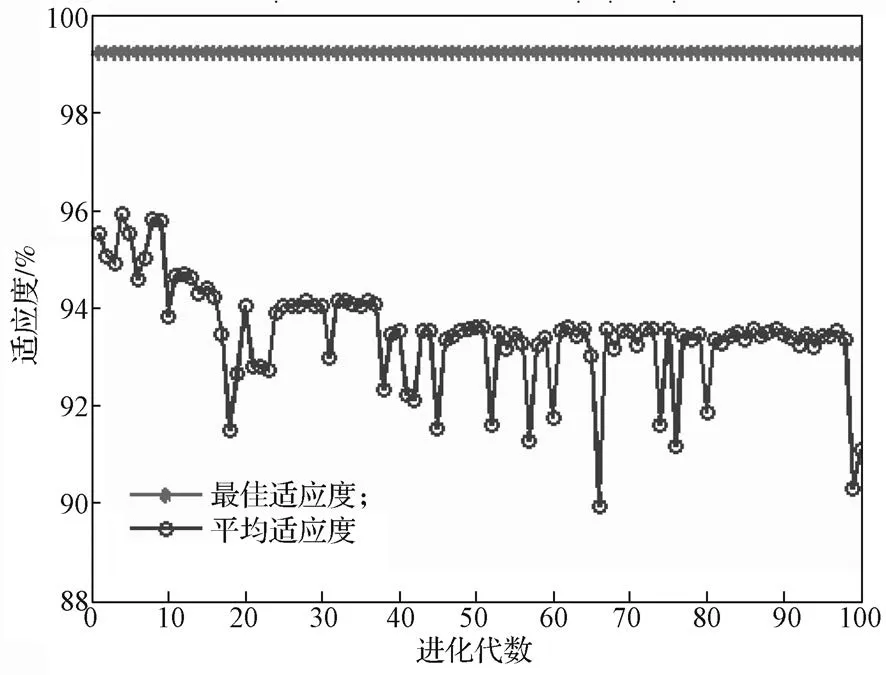
图3 CS-GA寻参的适应度曲线Fig. 3 Fitness curve of CS-GA
图3表明,CS-GA进化代数为100代时终止进化,此时平均适应度值为90.8%,接近理想最优值。
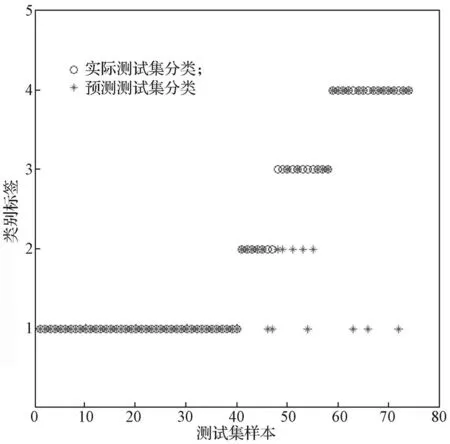
图4 测试集分类结果图Fig. 4 Classi fi cation results of test sets

表2 CS-GA-LS-SVM模型对各种黏着状态类别的分类准确率Table 2 CS-GA-LS-SVM model for the classi fi cation of various types of adhesion accuracy
表2的分类结果表明,CS-GA-LS-SVM能够很好地辨识重载机车的黏着状态,其中类别1的分类准确率达到100.00%,类别4测试集分类准确率达到96.00%。类别2和类别3测试集分类准确率略低于类别1和类别4的分类准确率。
5.2 遗传算法的支持向量机
遗传算法是一种基于自然选择和基因遗传学原理的随机并行搜索算法,是一种寻求全局最优解且不需要任何初始化信息的高效优化方法[13]。它将问题的解集看作一个种群,通过不断地进行选择、交叉、变异等遗传操作,使解的质量越来越好。该算法具有全局寻优能力、适应性强、能解决非线性问题、较强的鲁棒性等特点。课题组采用遗传算法优化支持向量机,并将此模型运用于重载机车黏着状态辨识。遗传算法寻找最佳参数的适应度曲线和测试集分类结果,如图5~6及表3所示。
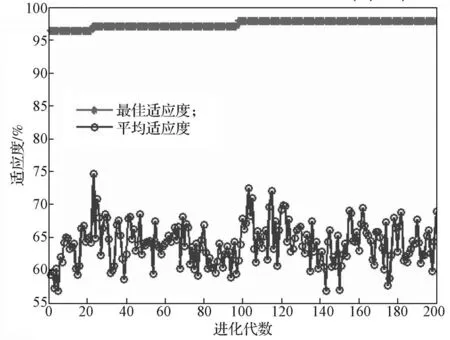
图5 遗传算法寻找最佳参数的适应度曲线Fig. 5 Determination of the fi tness curve of the best parameters based on genetic algorithm
由图5知,在90代左右,遗传算法的平均适应度达到稳定,进化代数为200代时终止进化,此时平均适应度值为68.5%。
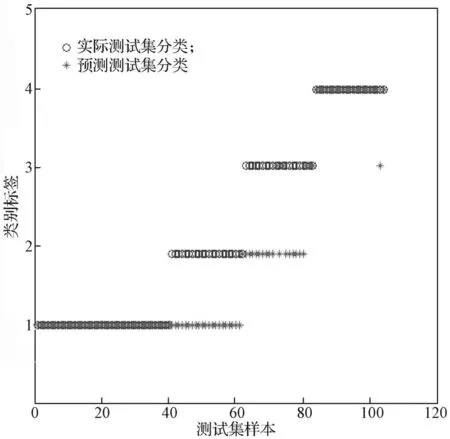
图6 测试集分类结果图Fig. 6 Classi fi cation results of test sets

表3 GA-SVM模型对各种黏着状态类别的分类准确率Table 3 GA-SVM model for the classi fi cation of various types of adhesion accuracy
由表2和表3的分类结果表明,采用多分类支持向量机可以有效地辨识重载机车的黏着状态,采用CS-GA-LS-SVM具有更高的准确率。
采用不同算法得到支持向量机的相关参数和分类准确率分别如表4所示。

表4 不同算法支持向量机的相关参数和分类准确率Table 4 Correlation parameters and classi fi cation accuracy of different algorithm support vector machines
表4的结果表明,CS-GA-LS-SVM对机车黏着状态识别具有较高的分类准确率,GA-SVM分类准确率最低。
5.3 极限学习机
极限学习机[14-15]是一种新型的单隐层前馈神经网络学习方法,它对大量非结构性、非精确性规律具有自适应能力、自主学习和优化计算的特点,只需训练前设置合适的隐层节点数,在执行过程中为输入权值和隐层偏置随机赋值,整个过程一次完成,无需迭代,并且产生唯一的最优解。课题组将多分类最小二乘支持向量机模型与极限学习机对比,所得结果如表5所示。

表5 不同分类器得到的分类结果Table 5 Classi fi cation results obtained from different classi fi ers
表5表明,CS-GA-LS-SVM训练集和测试集分类准确率均高于极限学习机,虽然极限学习机分类时间较短,但是其稳定性较差。
6 结语
课题组将多分类最小二乘支持向量机应用于重载机车黏着状态辨识,并提出将机车的黏着状态分为正常、故障征兆、微小故障和严重故障4个状态。课题组提出采用布谷鸟遗传算法优化最小二乘支持向量机的相关参数,避免了以往研究中选择参数的盲目性和随机性。通过与极限学习机算法和遗传算法寻优结果的对比分析,该方法能够获得较高的分类准确率,充分说明此方法在工程上具有更高的黏着状态辨识准确率。
近年来深度学习不断发展,黏着状态的数据特征差异细微,深度学习可以深度提取并分类,将会是黏着状态辨识的发展趋势。
[1]胡亚东. 我国铁路重载运输技术体系的现状与发展[J].中国铁道科学,2015,36(2):1-10.HU Yadong. Current Status and Development Trend of Technology System for Railway Heavy Haul Transport in China[J]. China Railway Science,2015,36(2):1-10.
[2]WANG S,XIAO J,HUANG J,et al. Locomotive Wheel Slip Detection Based on Multi-Rate State Identification of Motor Load Torque[J]. Journal of the Franklin Institute,2016,353(2):521-540.
[3]ZHAO Y. Low Adhesion Detection and Identification in a Railway Vehicle System Using Traction Motor Behaviour[D]. West York:University of Hudders fi eld,2013.
[4]陈慧楠. 基于输入约束在线辨识的高速列车主动粘着防滑牵引控制[D]. 北京:北京交通大学,2015.CHEN Huinan. Active Adhesion and Anti-Skid Based Traction Control of High Speed Trains Via Online Identification of Input Constraint[D]. Beijing:Beijing Jiaotong University,2015.
[5]李江红,胡云卿,彭辉水,等. 轨道交通粘着利用控制的关键技术与方法[J]. 机车电传动,2014(6):1-5.LI Jianghong,HU Yunqing,PENG Huishui,et al. Key Techniques and Design Methods of Adhesion Control in Rail Transportation[J]. Locomotive Electric Drive,2014(6):1-5.
[6]ALLOTTA B,MELI E,RIDOLFI A,et al. Development of an Innovative Wheel-Rail Contact Model for the Analysis of Degraded Adhesion in Railway Systems[J].Tribology International,2014,69(1):128-140.
[7]任 强. 重载机车粘着控制方法的研究与设计[D]. 成都:西南交通大学,2014.REN Qiang. Study and Design of Adhesion Control Methods of Heavy-Hual Locomotive[D]. Chengdu:Southwest Jiaotong University,2014.
[8]刘 帮,秦 斌,王 欣,等. PSO-LIBSVM在污水水质建模中的应用[J]. 湖南工业大学学报,2015,29(2):89-93.LIU Bang,QIN Bin,WANG Xin,et al. Application of PSO-LIBSVM in Modeling of Sewage Water Quality[J].Journal of Hunan University of Technology,2015,29(2):89-93.
[9]王 欣,宋翼颉,秦 斌,等. 基于LSSVM的污水处理过程建模[J]. 湖南工业大学学报,2016,30(1):59-63.WANG Xin,SONG Yijie,QIN Bin,et al. Modeling of Sew Age Treatment Process Based on MIMO-LSSVM[J].Journal of Hunan University of Technology,2016,30(1):59-63.
[10]薛浩然,张珂珩,李 斌,等. 基于布谷鸟算法和支持向量机的变压器故障诊断[J]. 电力系统保护与控制,2015(8):8-13.XUE Haoran,ZHANG Keheng,LI Bin,et al. Fault Diagnosis of Transformer Based on the Cuckoo Search and Support Vector Machine[J]. Power System Protection and Control,2015(8):8-13.
[11]KAVEH A,BAKHSHPOORI T,AZIMI M. Seismic Optimal Design of 3D Steel Frames Using Cuckoo Search Algorithm[J]. The Structural Design of Tall and Special Buildings,2015,24(3):210-227.
[12]SU Z,TANG B,LIU Z,et al. Multi-Fault Diagnosis for Rotating Machinery Based on Orthogonal Supervised Linear Local Tangent Space Alignment and Least Square Support Vector Machine[J]. Neurocomputing,2015,157:208-222.
[13]ROBERGE V,TARBOUCHI M,LABONTE G.Comparison of Parallel Genetic Algorithm and Particle Swarm Optimization for Real-Time UAV Path Planning[J]. IEEE Transactions on Industrial Informatics,2013,9(1):132-141.
[14]LI S,YOU Z H,GUO H,et al. Inverse-Free Extreme Learning Machine with Optimal Information Updating[J].IEEE Transactions on Cybernetics,2016,46(5):1229-1241.
[15]LU X,ZOU H,ZHOU H,et al. Robust Extreme Learning Machine with Its Application to Indoor Positioning[J]. IEEE Transactions on Cybernetics,2016,46(1):194-205.
(责任编辑:申 剑)
Adhesion State Identi fi cation Based on Least Square Support Vector Machines
LIU Linfan,HE Jing
(School of Electrical and Information Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China)
In view of the low classification accuracy in the identification of heavy duty locomotive adhesion state, a genetic algorithm based on cuckoo has been proposed to optimize the parameters of least squares support vector machines, with the cross validation method adopted to improve the overall generalization performance of the model.First, the cuckoo algorithm is used to fi nd the initial values of penalty parameters and kernel functions. Next, the genetic algorithm is used to train the least squares support vector machines (SVM), thus obtaining the best parameters of the least squares support vector machines (SVM) model. Under this classi fi cation model, the adhesion states of heavy duty locomotive can be divided into four categories: normal condition, fault symptom state, minor fault state and serious fault state. Experimental results show that the classi fi cation accuracy of the proposed least squares support vector machine model can reach as high as 94.59%, much higher than that of the limit learning machines with its classi fi cation accuracy only being 84.61%. Therefore it is proved that the genetic algorithm can effectively improve the classi fi cation accuracy of the least squares support vector machines.
least square support vector machine;cuckoo genetic algorithm;heavy haul locomotive;adhesion state;accuracy
TP181
A
1673-9833(2017)04-0044-06
10.3969/j.issn.1673-9833.2017.04.008
2016-12-09
湖南工业大学研究生科研创新基金资助项目(CX1707)
刘林凡(1989-),男,湖北黄梅人,湖南工业大学硕士生,主要研究方向为电力传动技术及其故障诊断,E-mail:xiaomumu@stu.hut.edu.cn
何 静(1971-),女,湖南株洲人,湖南工业大学教授,硕士生导师,主要从事机电系统和工业过程控制方面的教学与研究,E-mail:hejing @ 263.net

