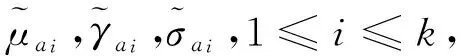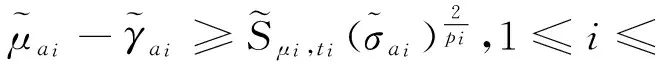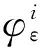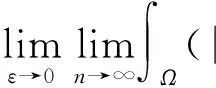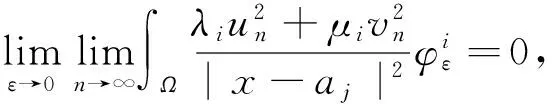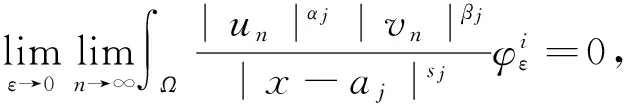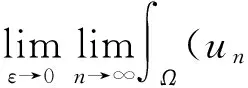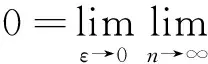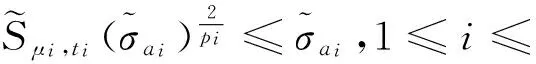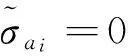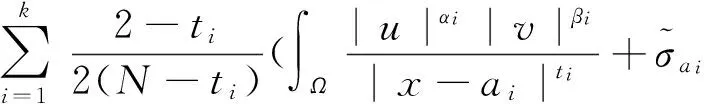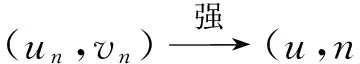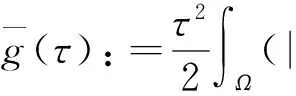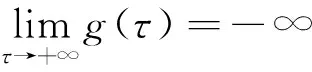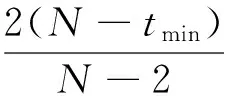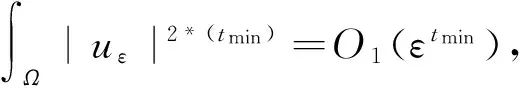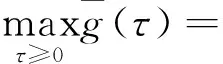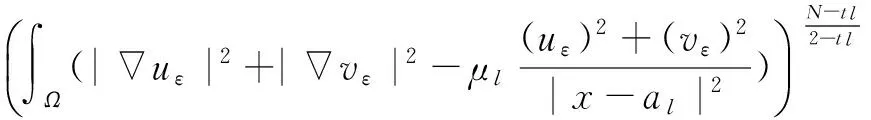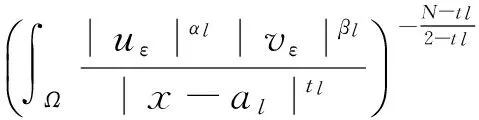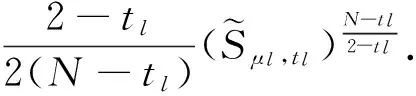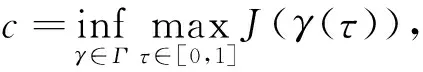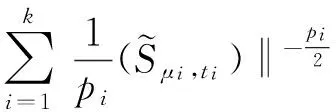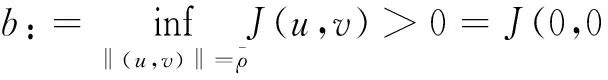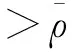一类带有多重Hardy项和多重强耦合Hardy-Sobolev临界项的椭圆方程组的正解

康东升，李 静，徐良顺

(中南民族大学 数学与统计学学院,武汉430074)

一类带有多重Hardy项和多重强耦合Hardy-Sobolev临界项的椭圆方程组的正解

康东升，李 静，徐良顺

(中南民族大学 数学与统计学学院,武汉430074)

研究了一类带有多重Hardy项和多重强耦合Hardy-Sobolev临界项的椭圆方程组，运用集中紧性原理和山路定理，控制Hardy项系数和强耦合临界项指数，证明了在一定条件下方程组正解的存在性，首次把带有多重Hardy项的临界椭圆方程的相关方法应用到带有多重Hardy项和强耦合Hardy-Sobolev临界项的椭圆方程组.

多重Hardy项；强耦合Hardy-Sobolev临界项；集中紧性原理；山路定理

AbstractIn this paper, an elliptic system is investigated, which involves multiple Hardy-type terms and strongly-coupled critical Hardy-Sobolev terms. By the concentration compactness principle and the Mountain Pass Theorem and by controlling the coefficients of Hardy-type terms and the exponents of strongly-coupled critical terms, the existence of positive solutions to the system is verified under certain conditions, and for the first time, the related methods for the critical elliptic equation involving multiple Hardy-type terms are extended to the system of critical elliptic equations involving multiple Hardy-type terms and strongly-coupled Hardy-Sobolev critical terms.

Keywordsmultiple Hardy-type terms; strongly-coupled critical Hardy-Sobolev term; concentration compactness principle; Mountain Pass theorem

1 相关知识

本文研究如下带有多重Hardy项和多重强耦合Hardy-Sobolev临界项的椭圆方程组：

(1)

其中Ω⊂N(N≥3)是有界光滑区域，方程组中的参数满足如下假设：

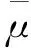
方程组(1)与下面的Hardy-Sobolev不等式密切相关[1]：

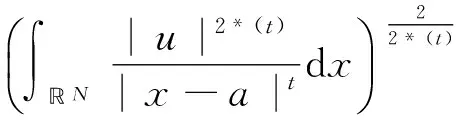
(2)

关于对应的最佳常数和极值函数，参见文献[2]和[3]．当t=2时(2)式就变成了著名的Hardy不等式[1]：

(3)

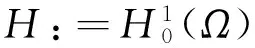
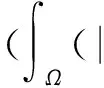
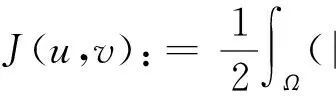
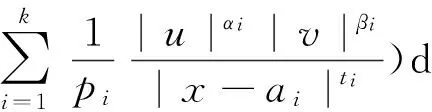
则J∈C1(H×H,).如果(u,v)≠(0,0)满足

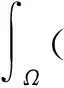
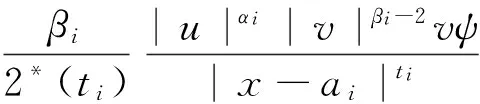
则称(u,v)∈H×H是方程组(1)的一个解.此时由椭圆方程的正则性理论可知:

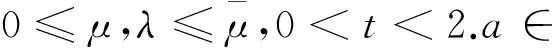
(4)

(5)

其中D1,2(N)是N)关于范数的完备化空间. 由文献[3]可知Sμ,t与a无关,并且Sμ,t有如下形式的达到函数：

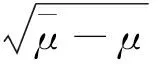
不失一般性，假设：

(M3) 存在l,1≤l≤k,使得0≤λl=μl<μ*，并且

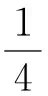
本文的主要结果可以归纳为下面的定理1.

定理1 假设条件(M1)，(M2)和(M3)成立，则方程组(1)在H×H中至少存在一个正解.

2 正解的存在性

首先需要建立几个定义和引理.

设泛函I∈C1(H×H,).如果对于任意满足下列条件的{(un,vn)}⊂H×H：

I(un,vn)→c,I′(un,vn)→0 在(H×H)*中，{(un,vn)}在H×H中都存在一个强收敛的子列，则称I满足(P.S.)c条件.

证明当n→∞时，假设{(un,vn)}⊂H×H满足：

J(un,vn)→c

其中δx是点x处的Dirac质量.由Hardy-Sobolev不等式，得出：

(6)

因此有：

(7)

于是由(6)、(7)式可得：

另一方面，推出：

证明证明过程与文献[6]的定理5类似，这里略去.

引理3[7]当ε→0时，有：

引理4 设：

则在定理1的假设条件下有：

证明考虑下面两个函数：

当ε→0时，由引理3可知，存在不依赖于ε的常数C1，C2>0，使得：

C1<τε

为了简单，假设：

tmin=min{tj:1≤j≤k,j≠l}∈(0,4).

直接通过计算得：

μl<μ*⟺2b(μl)>tmin.

(8)

另外，

由(8)式和引理3可得：

另一方面，

由引理2和3可以得出：

(9)

再由(9)式、引理3可得：

Γ={γ∈C([0,1],H)|γ(0)=0,J(γ(1))<0}.

对任意u∈H{0}，由不等式(2)和(3)可得：

J(un,vn)→c,J′(un,vn)→0.

由引理4可得出：

由引理1知在{(un,vn)}中存在子序列(仍记为{(un,vn)})，使得在H×H中(un,vn)→(u,v). 因此J存在一个临界点(u,v)满足方程组(1). 设u+=max{u,0},v+=max{v,0}，分别用u+,v+来替换方程组(1)中等式右边的u,v，重复上述过程可以得到方程组(1)的一个非负解(u,v)．由最大值原理[9]可以推出在Ω{0}中u,v>0.定理1证毕．

[1] Caarelli L, Kohn R, Nirenberg L. First order interpolation inequality with weights[J]. Compositio Mathematica, 1984, 53(1): 259-275.

[2] Catrina F, Wang Z. On the Caffarelli-Kohn-Nirenberg inequalities:sharp constants,existence(and nonexistence), and symmetry of extremal functions[J]. Communications on Pure and Applied Mathematics, 2001, 54(2): 229-257.

[3] Kang D, Peng S. Positive solutions for singular critical elliptic problems[J]. Applied Mathematics Letters, 2004, 17: 411-416.

[4] Lions P L. The concentration compactness principle in the calculus of variations, the limit case(II)[J]. Revista Mathematical Iberoamericana, 1985, 1(2): 45-121.

[5] Lions P L. The concentration compactness principle in the calculus of variations, the limit case(I)[J]. Revista Mathematical Iberoamericana, 1985, 1(1): 145-201.

[6] Alves C, Filho D, Souto M. On systems of elliptic equations involving subcritical or critical Sobolev exponents[J]. Nonlinear Analysis, 2000, 42(5): 771-787.

[7] Kang D, Li G. On the elliptic problems involving multi-singular inverse square potentials and multi-critical Sobolev-Hardy exponents[J]. Nonlinear Analysis, 2007, 66 (8): 1806-1816.

[8] Ambrosetti A, Rabinowitz H. Dual variational methods in critical point theory and applications[J]. Journal of Functional Analysis, 1973, 14(4): 349-381.

[9] Vazquez J. A strong maximum principle for some quasilinear elliptic equations[J]. Applied Mathematics and Optimization, 1984, 12(3): 191-202.

PositiveSolutionstoanEllipticSystemInvolvingMultipleHardy-TypeTermsandMultipleStrongly-CoupledCriticalHardy-SobolevTerms

KangDongsheng,LiJing,XuLiangshun

(College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China)

O175.25

A

1672-4321(2017)03-0137-05

2017-04-11

康东升(1967-)，男，教授，博士，研究方向：偏微分方程，E-mail:dongshengkang@scuec.edu.cn

国家自然科学基金资助项目(11601530);中南民族大学研究生科研创新项目(2017sycxjj083)