基于拟牛顿法改进的3D正态分布变换点云配准算法
王 鹏,李少达,赵 雪
(1.成都理工大学 地球科学学院,四川 成都 610059;2.西南交通大学 地球科学与环境工程学院,四川 成都 611756)
0 引 言
地面激光扫描技术以速度快,高精度获取3维数据的特点,广泛应用于3D重建,滑坡监测,文物保护,城市规划等领域[1]。由于地面激光扫描仪需固定设站的缺陷,目标物体的完整数据需要进行不同角度的多次扫描才能获取。因为每次扫描数据都是基于仪器默认的局部坐标系,因此需要将不同坐标系下的扫描数据统一到同一坐标系,即点云配准。
3D正态分布算法(3D Normal Distribution Transform,3D-NDT)于2009年被首次提出[2-3],并成功应用在3D点云配准中,而且相对于经典的ICP[4]算法有更好的精度和收敛速度。但是3D-NDT仍然有需要较好的初始值,参数难以确定等问题。随后,多层NDT(MLNDT)算法[5]被提出,并在一定程度上降低了参数难确定性的复杂性。同时针对3D-NDT算法需要较好初始值的问题,基于SIFT特征的3D-NDT点云自动配准算法[6],基于曲率特征的3D-NDT点云配准算法[7],结合NARF的3D-NDT自动配准算法[8]被相继提出。虽然与3D-NDT算法相比ICP[4]算法能够快速高精度地进行点云配准,但是面对不断增加的大量高密度点云数据,配准效率仍然是一个难题[9]。因此,本文在已有研究的基础上,针对3D-NDT算法在大型点云配准中效率低的问题,提出基于拟牛顿法的3D-NDT算法。
1 拟牛顿法改进的3D-NDT算法
1.1 3D-NDT算法原理
3D-NDT的目标是找到当前扫描点在参考扫描点云表面匹配的似然函数最大化时的姿态。3D-NDT算法首先将三维点云数据集均匀地划分为规则立方体,每个立方体内包含一定数量的点x={x1,x2,…,xn}。对于立方体中每一个点xi的概率密度函数可以表示为:

式中,x-和V分别表示立方体内点云的均值和方差。
3D-NDT算法通过当前扫描点云经过初始坐标转换参数映射到参考扫描点云中的概率密度之和s(p)作为坐标变换参数的分数值进行评价。因此两视点云的最优转换参数求解过程,就转换成了概率密度之和s(p)的最优化问题。

式中,xi'表示当前扫描点映射到参考扫描表面的坐标。T(p,xi)表示当前扫描点的坐标转换。
1.2 拟牛顿法改进
最优化问题通常被看成最小化问题,因此,3D-NDT求解最优参数的过程即s(p)最小化过程。3D-NDT是通过牛顿迭代法求解最优参数,令ƒ=s(p)为目标函数,为使目标函数最小需求解以下方程:

其中g为f的梯度,用一阶导数表示,H为Hessian矩阵,用ƒ的二阶导数表示。
从式(3)可以看出,Hessian矩阵的求解需要计算目标函数的二阶导数。但是目标函数的二阶导数计算复杂,特别是随着点云数量的增加,二阶导数的计算需要消耗大量的时间。而拟牛顿法(Quasi-Newton Methods)作为求解非线性优化问题最有效的方法之一[10]。他通过近似Hessian矩阵的方式代替通过二阶导数求解Hessian的过程,能够解决牛顿迭代法需要计算复杂二阶导数的问题。因此,本文具体采用拟牛顿法中的DFP方法对3D正态分布变换算法进行优化。
DFP算法首先假设Heissian矩阵为单位阵I,计算搜索方向Δp=-Hkgk(Hk为Hessian矩阵,gk为梯度)。然后通过校正方程更新Hessian的值,不断逼近Hessian的真实值,直到算法收敛。校正方程如下:

式中,sk=λkΔp,λk=argminƒ(xk+λΔp),yk=gk+1-gkgk+1,gk表示参数为xk+1,xk时,函数ƒ对应梯度值。
1.3 拟牛顿法改进的3D-NDT算法步骤
针对3D-NDT算法中Hessian矩阵计算复杂,导致配准效率降低的问题,提出拟牛顿法改进的3D-NDT点云配准算法。假设x为源点云,y为参考点云,将源点云x配准到参考点云y的具体步骤如下:
①建立参考点云y的正态分布变换;
②根据转换参数 将点云x中的点转换到到点云y中,得到x';
③计算点云x'中每一个点的正态变化分布;
④计算点云x'中每一个点的概率之和s(p)。
⑤根据式(4)得到Hessian矩阵优化s(p),得到Δp;
⑥若算法达到收敛条件Δp<ε则停止,否则更新转换参数p=p+Δp继续转至步骤②如图1所示。

图1 算法流程图Fig.1 Algorithm flowchart
2 实验结果
在ubuntu16.04操作系统(内存3G,处理器1核)上,采用C++语言结合点云数据库(point cloud library,PCL)实现编程,为验证本文算法的精度和效率,实验数据采用PCL官方网站(www.pcl.org)提供的一组室内采集的样例数据(两视点云cloud1、cloud2数据量分别为112,586,112,624),对本文算法与3D-NDT算法进行对比测试,参数设置中最大迭代次数50,收敛条件为两次迭代参数结果之差小于0.01,配准精度采用均方根误差(Root Mean Squared Error,RMSE)进行对比。
在试验中分别对点云cloud1进行尺寸分别为0.1,0.2,0.3的三维体素格网采样,得到3组不同数量的点云数据(见表1)。实验结果见表2。通过拟牛顿法改进的3D-NDT算法大大提高了算法的配准效率,而且随着点云数量的增加本文算法在配准效率方面的优势更加明显,。同时,本文算法的配准精度与原算法基本保持不变。

表1 实验数据Tab.1 Experimental data
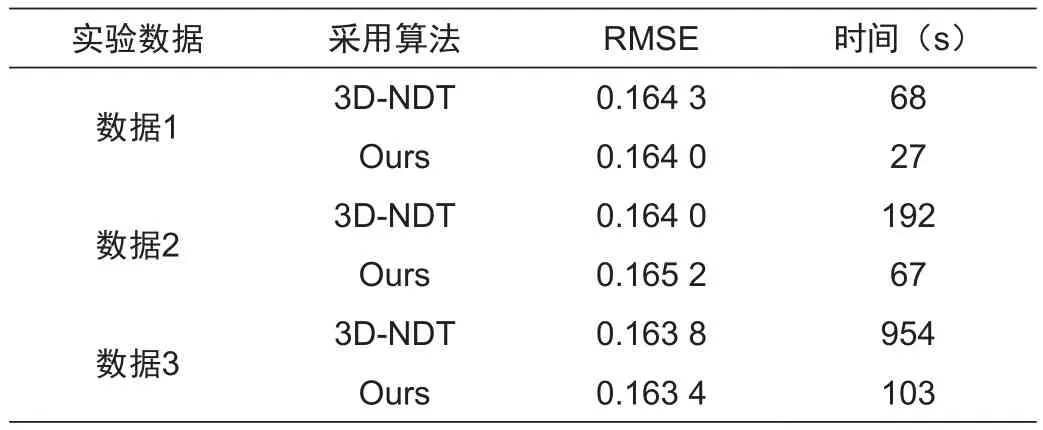
表2 点云数据采样配准算法实验结果对比Tab.2 Comparison of experimental results of sample point cloud registration algorithm
3 结束语
本文针对牛顿法Hessian矩阵计算复杂的特点,提出了基于拟牛顿法的3D正态分布变换算法,在精度保持不变的情况下,提高了3D正态分布算法进行点云配准的效率。但是,3D正态分布算法的参数如最大步长,格网大小很难快速确定最优值,这些参数的快速确定将是下一步的研究方向。

