弱混合陆相河口的河床稳定性判据

高仕赵冀自清尤再进

(1.鲁东大学 土木工程学院,山东 烟台264025;2.清华大学 水沙科学与水利水电工程国家重点实验室,北京100084)

弱混合陆相河口的河床稳定性判据

高仕赵1,冀自清2,尤再进1

(1.鲁东大学 土木工程学院,山东 烟台264025;2.清华大学 水沙科学与水利水电工程国家重点实验室,北京100084)

针对弱混合陆相河口的河床稳定性问题,应用雷诺时均化法将潮流和径流的振荡效应以雷诺切应力的形式反映出来,利用由雷诺切应力构造出的广义力、广义流以及最小能耗率原理建立了弱混合陆相河口的能耗率,应用变分原理对弱混合陆相河口的能耗率进行极值分析得出河床的稳定性判据。根据河床的稳定性判据可得：河床的稳定性与流速梯度以及平均流速相关。另外,应用楔形水槽模型计算了不同坡度下的单位体积水流能耗率的变化。结果表明：当楔形水槽内的水体发生扰动时,能耗率增加,但随着水体的自我调整,能耗率随之减小,最后达到能耗率最小的稳定状态,因此水槽中的水体遵循最小能耗率原理。进而也间接验证了稳定性判据的适用性。

弱混合陆相河口;最小能耗率原理;河床稳定性判据;雷诺时均法

稳定的河口河床是能够保证其河口形式不发生剧烈变化以及河床能够较长时间维持冲淤平衡,这对于在海岸河口地区建设港口、开挖航道、修建防波堤非常重要。而河口河床稳定性又受潮流和径流等外界动力因素的影响。这些动力因素也同时影响着河口形式。由于我国的独特地理位置导致了南方地区的河口多以潮流为主、径流为辅,而北方地区的河口却多以径流为主、潮流为辅,因此北方地区的河口形式以弱混合陆相河口特点为主[1-2]。弱混合陆相河口具有3个明显的特征：1)潮流较小且较弱,径流相对较强,受潮汐影响的河段较短;2)洪水季节潮汐影响只在河口附近,泥沙主要来自流域;3)在来沙比较丰富的情况下,径流携带大量泥沙,往往就在口门附近淤积,使河床抬高,河床的纵剖面向上游倾斜呈显著的倒比降。基于弱混合陆相河口的特点,可知影响其河床变化的主要因素是径流场和潮流场。因此,在建立弱混合陆相河口的数学模型时,可以主要考虑径流场和潮流场的影响,并对简化后的模型进行时均化处理,将反复变化的振荡流以时均处理后的雷诺切应力反映出来。另外,弱混合陆相河口系统(简称为“河口系统”)属于开放系统,主要受来自径流场、潮流场联合作用的影响。当河口河床的底坡适应来水来沙时,河口系统处于平衡状态。河口系统这种宏观的平衡态实际建立在无数微观沙粒冲淤平衡的基础上,此时的河口系统符合“经典热力学理论”模型(即宏观表现是由大量微观粒子的“平均表现”所决定的)。当河口系统处于扰动(如上游来水来沙量发生变化)所引起的非平衡态时,河口系统内各个组成部分的性质不再均匀,它的流场、输沙率也会随时间变化,河口系统不再符合“经典热力学理论”模型。此时的河口系统从整体上看是处于非平衡态,但如果将河口系统等效成由很多微小局域子系统所组成,并且每个局域子系统都处于平衡态。而这些局域子系统之间确存在着差异,从整体来看整个河口系统仍然处于非平衡态。因此,处于扰动状态的河口系统符合“最小能耗率原理”模型。

Helmholtz最早将最小能耗率原理(最小熵产生原理与最小能耗率原理是等价的)应用于流体研究,他于1868年提出了适用于缓慢黏性流动的最小能耗率原理。经过半个多世纪之后,非线性热力学在流体方面的研究进展缓慢[3]。直到20世纪50年代前苏联学者维里坎诺夫(ВепикановMA)才将最小能耗率原理扩展到河流动力学领域[4]。目前应用非平衡态热力学于河流动力学研究最具影响力的当属Chang[5],Yang[6],Yang和Song[7-8],Song和Yang[9],Yang和Molins[10]运用变分极值方法从力学角度推导的河流最小能耗率原理。但Yang[6],Yang和Song[7-8],Song和Yang[9]提出的最小能耗率原理适用条件为不与外界进行任何物质和能量交换的封闭孤立系统,而孤立系统不存在最小能耗率。徐国宾和杨志达[11]对最小能耗率原理适用条件进行了完善,将其适用条件扩展到开放系统,并运用最小能耗率原理解释了河流成因,同时建立了显示河相关系并将其应用于稳定渠道的优化设计以及渠首引水防沙工程中[12-14]。而河口系统属于开放系统,因此,弱混合陆河口系统的河床稳定性问题仍然适用于最小能耗率原理。

(王 燕 编辑)

1 理论分析

弱混合陆相河口的河床演变问题必然遵循连续方程和Navier-Stokes方程,但由于潮流的振荡效应直接应用以上方程进行求解非常困难。目前,普遍采用的方法是对瞬时的Navier-Stokes方程进行时均化处理,将振荡量通过湍流模型在时均化的方程中体现出来,即雷诺平均法。

流体运动的连续性方程：

式中,ui(i=1,2,3)为速度分量;xi(i=1,2,3)为坐标分量。

Navier-Stokes方程：

式中,t为时间;fi为体积力分量;p为压强;ρ为密度;υ为运动黏度系数;i=1,2,3;j=1,2,3。

根据式(1)和式(2)的等号左侧,可变为

将式(4)代入式(2)并结合式(3),再对式(1)和式(2)进行时均化处理,得：

根据普朗特混合长度理论以及类比牛顿内摩擦定理,可得雷诺附加应力τ'ij：

式中,i=1,2,3;j=1,2,3;l为普朗特混合长度;μt为紊动动力黏滞系数。

雷诺附加应力：

将式(7)代入式(6)得：

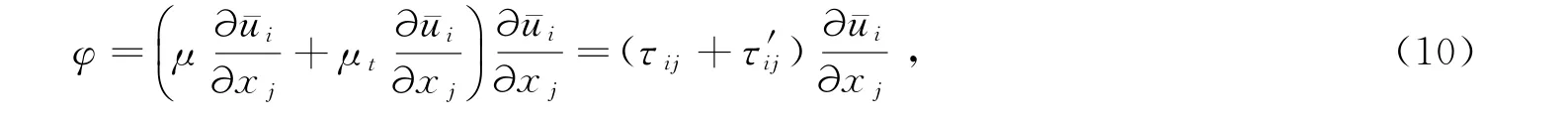
式中,τij(i=1,2,3;j=1,2,3)为流体黏度引起的切向应力。

流体在单位时间内的总能耗率Φ为

式中,dV为单位体积元;ni为面积元dΩ的外法线方向的单位矢量的分量。

设流体的长期平均效果为恒定流,即所有的时均参量不随时间变化(如u-i,p-等),流体运动具有稳定边界条件,此时,式(11)等号右侧曲面积分为零。因此,流体在单位时间内的总能耗率Φ为

又由于：

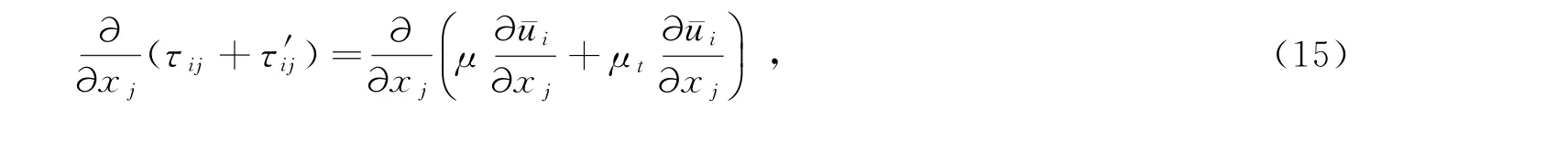
因此,式(13)可变为

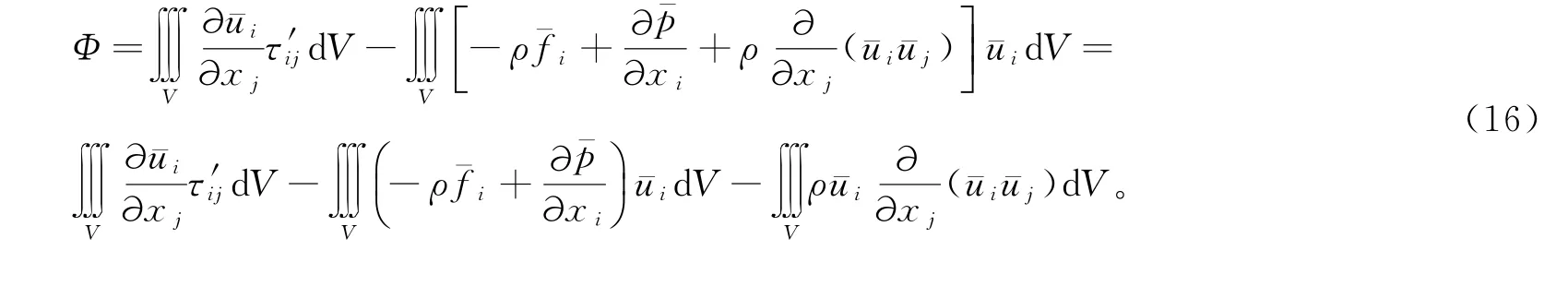
应用高斯公式,式(16)可化简为

所以,式(18)为零,式(16)可简化为

式中,h为铅垂方向的向量(向上为正);g为重力加速度。由于h和g与坐标轴共线,因此在后面推导过程中直接采用h和g的模。

则式(19)可表示为

因此,局域能耗率函数φ为

弱混合陆相河口系统符合最小能耗率原理,因此,可以应用超能耗率δXΦ来判断弱混合陆相河口稳定性。计算超能耗率δXΦ的公式为

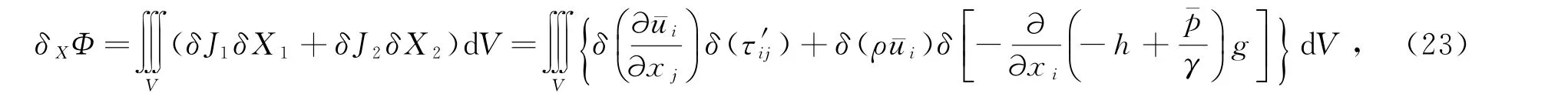
式中,δJ1和δJ2为广义流变的分;δX1和δX2为广义力的变分。

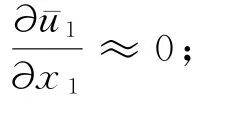
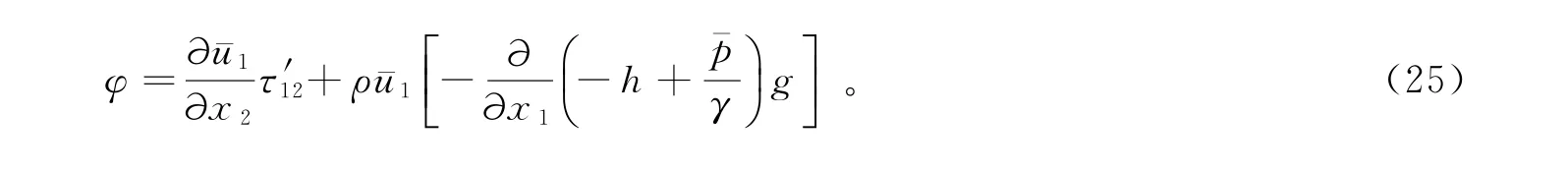
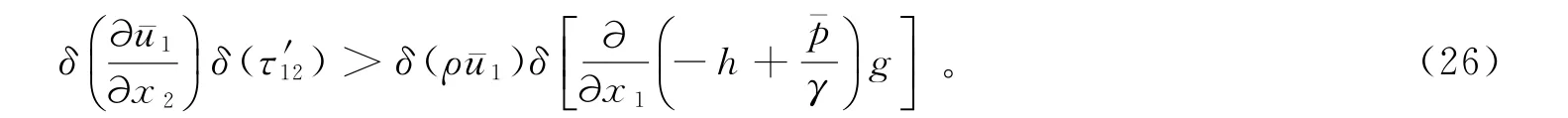
根据变分法则以及谢才公式(本文整个推导过程中所有参量都取一段时间的平均效果,因此符合谢才公式应用条件),得[11]：

依据式(25),当弱混合陆相河口稳定时,即δxφ＞0,可得：

雷诺剪切应力的变分：

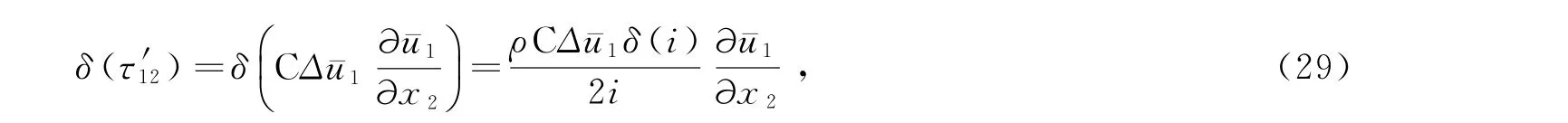
式中,C为普朗特经验常数;Δu-1为同一点沿深度方向最大速度变化量。

质量流的变分：

水力梯度的变分：

根据式(28)～式(31),式(26)可化简为

即当式(32)成立时,弱混合陆相河口处于稳定状态。

同理,弱混合陆相河口处于临界状态的判据为

弱混合陆相河口处于不稳定状态的判据为

2 数值模型计算

式(32)～式(34)是本文中最小能耗率原理的推论结果,但直接检验它们存在困难。为了论证结果的准确性,本文进而建立了楔形水槽数值模型,检验最小能耗率原理在弱混合陆相河口系统中的适应性[12],并间接论证本文结论的准确性。

建立的数值水槽长度为100m,上游入口处尺寸为15m×10m,下游出口处尺寸为20m×10m(图1)。基于图1,建立数值模型,其边界条件如图2所示,上下游采用压力边界条件,入口处水深为7.5m,出口处的水深为6.5 m,其他边界采用对称边界条件。水槽按照底坡(i)变化情况(图3)进行数值仿真计算,本文采用5种底坡(i1,i2,i3,i4,i5)变化形式对能耗率进行考察。在计算过程中,水槽中的水体随着底坡的不断变化,将由计算开始的恒定流逐渐变化为非恒定流,最后再变为恒定流。

图1 水槽尺寸示意图Fig.1 Dimension sketch map of the flume

图2 楔形水槽边界条件Fig.2 Boundary conditions of the wedge-shaped flume

本文采用5种底坡变化形式对能耗率进行了分析(图4),结果表明：楔形水槽中的水体随着底坡的变化呈现恒定流—非恒定流—恒定流的流动趋势。当水流初次达到恒定流时,单位体积水体能耗率为常值。当楔形水槽底坡发生变化后,其内的流体开始由恒定流变为非恒定流,单位水体的能耗率也开始增加。当楔形水槽底坡停止变化时,楔形水槽内的水体会自动调节各水力要素,使其逐渐恢复恒定流,此时单位体积水体能耗率又恢复为常值。由于施加在前后2次恒定流上的底坡条件不同,所以,2次恒定流的能耗率数值也不同。同时也可以看出,负向底坡越大,能耗率越大,这主要是由底坡增大流速降低所导致的。

图3 楔形水槽底坡时间变化图Fig.3 Changes of the bottom slope of the wedge-shaped flume with time

图4 总能耗率随底坡变化图Fig.4 Changes of the total energy consumption rate with the bottom slope

另外,通过对楔形水槽的数值分析表明：由于受外界干扰因素的影响,水体由稳态变为非稳态时,能耗率也随之增加;当外界干扰因素消退时,水体会自我恢复到能耗率最小的状态。因此,最小能耗率原理适用于弱混合陆相河口系统。

3 结 语

目前,河口河床稳定性问题仍然是河流动力学领域待解决的难题之一,本文从非平衡态热力学的角度对弱混合陆相河口进行了研究。通过将河口系统与热力学开放系统建立起联系,应用最小能耗率原理得出了河床底坡与平均流速以及流速梯度之间的关系式。运用此关系式可以初步判断弱混合陆相河口河床的稳定状态。需要指出的是,本文提出的河口河床稳定性判据是针对弱混合陆相河口,对于其他类型的河口,如强混合海相河口、缓混合海相河口等,不再适用,主要是由于其他类型河口的径流和潮流的强弱发生了改变,理论上推导的假设条件(即以雷诺切应力反映潮流和径流的振荡效应)不再成立。

[1] YING M,LI J F,CHEN S L,et al.Dynamics characteristics and topographic profile shaping process of Feiyan shoal at the Yellow River delta[J].Marine Science Bulletin,2008,10(2)：74-88.

[2] BAI Y C.Estuarine sediment movement mechanics[M].Tianjin：Tianjin University Press,2011.白玉川.河口泥沙运动力学[M].天津：天津大学出版社,2011.

[3] HOU H C.Basic problems of river dynamics[M].Beijing：Water Resources Press,1982.侯晖昌.河流动力学的基本问题[M].北京：水利出版社,1982.

[4] XU G B.Theory of non-equilibrium thermodynamics and its application for field of river dynamics[D].Tianjin：Tianjin University,2002.徐国宾.非平衡态热力学理论在河流动力学领域中的应用[D].天津：天津大学,2002.

[5] CHANG H H.Energy expenditure in curved open channels[J].Journal of Hydraulic Engineering,1983,109(7)：1012-1022.

[6] YANG C T.Unit stream power equation for gravel[J].Journal of Hydraulic Engineering,1984,110(12)：1783-1797.

[7] YANG C T,SONG C C S.Theory of minimum energy and energy dissipation rate[J].Encyclopedia of Fluid Mechanics,1986,1(11)：353-399.

[8] YANG C T,SONG C C S.Theory of minimum rate of energy dissipation[J].Journal of the Hydraulics Division,1979,105(7)：769-784.

[9] SONG C C S,YANG C T.Minimum energy and energy dissipation rate[J].Journal of the Hydraulics Division,1982,108(5)：690-706.

[10] YANG C T,MOLINAS A.Sediment transport and unit stream power function[J].Journal of the Hydraulics Division,1982,108(6)：774-793.

[11] XU G B,YANG Z D.Analysis of river bed changes based on the theories of minimum entropy production dissipative structure and chaos[J].Journal of Hydraulic Engineering,2012,43(8)：948-956.徐国宾,杨志达.基于最小熵产生与耗散结构和混沌理论的河床演变分析[J].水利学报,2012,43(8)：948-956.

[12] XU G B,ZHAO L N.Analysis of channel pattern changes in the lower Yellow River based on the rate of energy dissipation[J].Journal of Hydraulic Engineering,2013,44(5)：622-626.徐国宾,赵丽娜.基于能耗率的黄河下游河型变化趋势分析[J].水利学报,2013,44(5)：622-626.

[13] ZHAO L N,XU G B.Discriminant of stability for channel pattern based on excess entropy production[J].Journal of Hydraulic Engineering,2015,46(10)：1213-1221.赵丽娜,徐国宾.基于超熵产生的河型稳定判别式[J].水利学报,2015,46(10)：1213-1221.

[14] CHANG M,XU G B.Numerical simulation of fluid motion in flume based on theory of minimum rate of energy dissipation[J].Journal of Sediment Research,2013(2)：67-71.常美,徐国宾.最小能耗率原理的数值水槽模拟验证[J].泥沙研究,2013(2)：67-71.

Abstract：For the stability criteria of the riverbed in the weakly mixed terrestrial estuary,the oscillation effect of tidal current and run-off is reflected in the form of Reynolds shear stress by using Reynolds time average method.The energy consumption rate of the weakly mixed terrestrial estuary is established by using the generalized force and generalized flow constructed through Reynolds shear stress and according to the principle of minimum energy consumption rate.And then,the stability criteria of the riverbed are obtained by the external value analysis of the energy consumption rate of the weakly mixed terrestrial estuary by using the variance principle.According to the criteria,the stability of the riverbed is correlated to the flow velocity gradient and the mean flow velocity.Moreover,the changes of energy consumption rate per unit volume flow at different slope are calculated by using a wedge-shaped flume model.The results indicate that the energy consumption rate of the flow will increase when the water body in the wedge-shaped flume is disturbed,and with the self-adjustment of the water body,the energy consumption rate decreases and finally reaches to the minimum energy consumption steady state.Therefore,the water body in the flume follows the principle of minimum energy consumption rate.These have also indirectly verified the applicability of the stability criteria of the riverbed.

Key words：weakly mixed terrestrial estuary;principle of minimum energy consumption rate;riverbed stability criteria;Reynolds time average method

Received：March 28,2017

Stability Criteria of the Riverbed in the Weakly Mixed Terrestrial Estuary

GAO Shi-zhao1,JI Zi-qing2,YOU Zai-jin1
(1.School of Civil Engineering,Ludong University,Yantai 264025,China;2.State Key Laboratory of Hydroscience and Engineering-Tsinghua University,Beijing 100084,China)

TV143

A

1002-3682(2017)03-0001-08

10.3969/j.issn.1002-3682.2017.03.001

2017-03-28

山东省优秀中青年科学家科研奖励基金项目——基于非平衡态热力学理论的潮汐河口泥沙演变研究(BS2014SF016);山东省“泰山学者”人才工程项目——海岸侵蚀和淹没灾害数据采集和预测技术(+shw201502050)

高仕赵(1983-),男,副教授,博士研究生,主要从事水利水电工程方面研究.E-mail：wooden20030044@126.com