罗布麻纤维混纺织物综合性能分析与混纺比优选设计
顾秦榕 谢春萍 吉宜军 苏旭中 刘新金
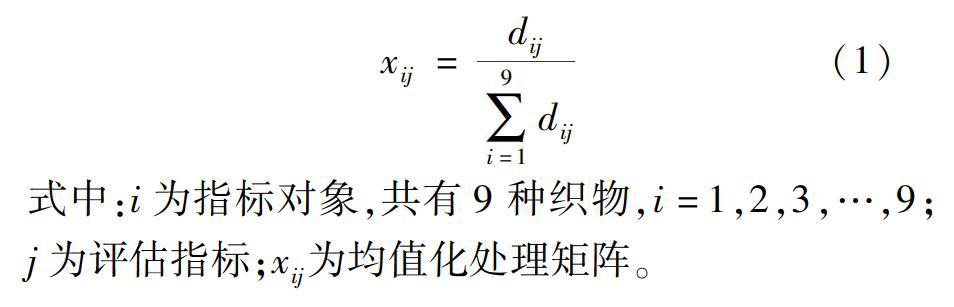
摘要: 罗布麻纤维是一种天然纤维,其功能保健性混纺产品的开发正愈来愈受到人们的欢迎。文章采用灰色聚类分析法对罗布麻/腈纶/莫代尔混纺针织物与亚麻/棉混纺针织物的综合性能进行研究,优选出罗布麻/腈纶/莫代尔混纺针织物性能良好。采用线性加权和法建立一种多目标化函数的优化模型,求解出用于不同生产用途的织物的最佳混纺比。结果表明:罗布麻/腈纶/莫代尔织物的综合性能优于亚麻/棉混纺织物与纯棉织物;当罗布麻纤维理论含量为20%、29%及50%时分别可以达到织物加工性能优良、外观效应佳、保健性好的设计效果。
关键词: 灰色聚类分析;线性加权和法;罗布麻;混纺比;优化
中图分类号: TS102.229
文献标志码: A
文章编号: 1001-7003(2017)12-0054-05
Abstract: Apocynum fiber is a natural fiber. The development of functional blended products is becoming more and more popular. In this paper, grey clustering analysis was used to study combination properties of apocynum/ acrylic fibers/ modal blended fabrics and linen/cotton blended fabrics, and the performance of apocynum/ acrylic fibers/ modal blended fabrics was good. The linear weight sum method was applied to establish an optimization model of multi-target function so as to solve the optimal blending ratio of different fabrics. The results show that, the comprehensive performance of the apocynum/ acrylic fibers/ modal blended fabrics is better than that of linen /cotton blended fabric. The design effect of good processing property, appearance and health keeping can be achieved when theoretical content of apocynum fiber is 20%,29% and 50%, respectively.
Key words: grey clustering analysis; linear weight sum method; apocynum; blending ratio; optimization
目前,在研究具有多個要素的对象时,传统的科学研究思维方式正逐步向系统论方法过渡[1]。系统论方法主要以把握整体性、综合性、相关性、动态性为基本原则,它是一种在多个要素彼此制约、相互联系的关系中,系统地分析研究对象的方法。
本文将灰色聚类分析[2]与线性加权和法[3]这两种思想引入到织物混纺比设计中,灰色聚类分析是指在信息不完全与非唯一的情况下,通过对少量的已知信息延伸并研究,进而上升到对系统的探究,寻找优化方法获得最佳效果的算法。线性加权和法是按照加工目标的重要性分别赋予其对应的权系数,通过线性组合求最优的一种多目标规划问题的方法。以罗布麻、亚麻混纺织物为例,采用灰色聚类分析法综合评定两类织物的优劣性,先对比优选出较优的织物。然后将麻纤维含量视为决策变量,将麻类混纺织物的各项基本性能视为目标函数,采用Matlab软件Cftool工具箱对实验数据进行拟合,得到目标函数。分别从织物的不同用途赋予目标函数不同的加权系数,将多目标函数转化成单目标函数,对函数进行求解,得到不同用途时织物的最佳混纺比。通过灰色聚类分析及Matlab优化模型的建立,从新的角度对纺织产品混纺比进行优化设计,为混纺织物的设计与开发提供理论性的依据。
1 织物的优选
1.1 仪器与材料
仪器:YG301破裂试验机、YG(B)522型耐磨试验机(南通宏大实验仪器有限公司),HH-4型数显恒温水浴锅芯吸效应测试仪(江苏盛蓝仪器制造限公司),YG(B)416E型数字式测试仪测量织物的透气性(宁波纺织仪器厂),PhabrOmeter织物手感评价系统(美国欣赛宝科技有限公司)。
织物:织物组织采用平针,平方米质量146g/m2,厚度0.37mm,横密62线圈数/5cm,纵密49线圈数/5cm。
1.2 实 验
由于织物的性能较多,且每种性能代表不同的含义,彼此之间联系较少,很难简单地评价织物性能的好坏,因此采用灰色聚类分析法来综合评价织物的性能。本文分别采用YG 301破裂试验机测量织物的顶破性,YG(B) 522型耐磨试验机测量织物的耐磨性,HH-4型数显恒温水浴锅芯吸效应测试仪测量织物的毛细芯吸性能,YG(B) 416E型数字式测试仪测量织物的透气性,PhabrOmeter织物手感评价系统测试织物的风格效应,按照纺织品抗菌性能测试标准GB/T209944.3—2008《纺织品 抗菌性能的评价 第3部分:振荡法》测试织物对大肠杆菌的抑菌效应。每块试样测试10组数据取平均值,测试数据如表1所示,其离散系数在5%~15%范围内。
1.3 矩阵的构建
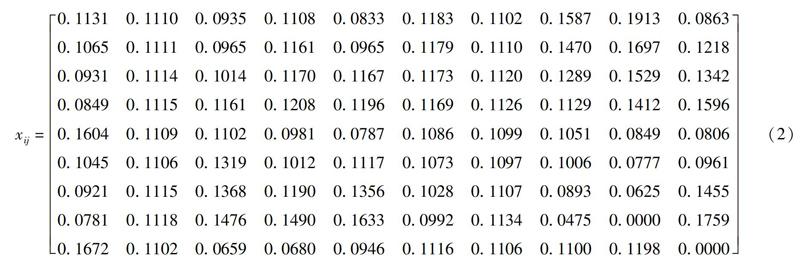
本文选取9种织物的顶破性、耐磨性、芯吸效应、透气性、硬挺度、柔软度、光滑度、悬垂性、手感值、抗菌性这10个评价因子构造矩阵dij。由于耐磨性的评价指标是失重率,失重率越大耐磨性越差,可以看出耐磨性与聚类指标呈负相关,为了使所有的评价因子与聚类指标关系保持统一性,将耐磨性数值以100减去失重率记录,得到织物剩余重量百分率,使得织物耐磨性与聚类指标呈正相关。其次测试的数据彼此之间没有联系,因此需要将它进行均值化处理从而变成无量纲数值[4]。利用Matlab软件将矩阵dij根据公式(1)均值化处理后得到一个9×10的均值化处理矩阵,如式(2)所示。
1.3 聚类系数的确定
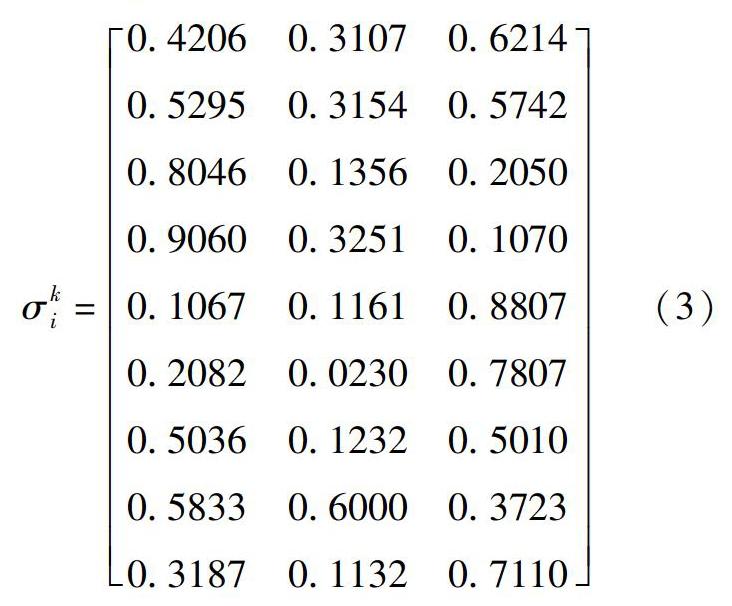
聚类系数表示一个图形中节点聚集程度的系数,聚类系数越大,相当于在这个灰度区间内出现的概率越大。将各因子的评价等级分为高类、中类、低类三种灰度等级[5],记为K1、K2、K3,即灰度s为3。根据边界值λjk与白化权函数fkj(x)确定指标j在聚类中的聚类系数[5],从而确定织物的综合性能,灰色聚类系数矩阵σki如式(3)所示。
根据综合聚类系数,即公式(3),在同一灰度下比较各织物的优劣等级,可以看出罗布麻48/腈纶20/莫代尔32与罗布麻40/腈纶33/莫代尔27织物的高类灰度区间的聚类系数分别是0.9060与0.8046,相比于其他混纺织物优势明显。9种织物的综合性能的排名依次是:罗布麻48/腈纶20/莫代尔32>罗布麻40/腈纶33/莫代尔27>罗布麻34/腈纶43/莫代尔23>罗布麻30/腈纶50/莫代尔20>亚麻43/棉57>纯亚麻>棉>亚麻30/棉70>罗布麻30/棉70。当罗布麻含量达到40%及以上时,织物的综合性能最佳;且罗布麻/腈纶/莫代尔的综合性能比亚麻混纺织物与棉织物好。由此可以进一步研究根据不同的生产用途,设计罗布麻/腈纶/莫代尔混纺织物的理论最优混纺比。
2 优化模型的建立
2.1 目标函数
本文研究的目标织物为罗布麻/腈纶/莫代尔混纺织物。研究对象是织物的综合性能,而不是单一的性能,把每个性能看成一个目标,研究多目标的最优问题。因此需要建立一个多目标函数,设有n个目标,目标函数分别为F1(x)、F2(x)、F2(x)……Fn(x)[6]。多目标函数的优化设计就是求解max{F1(x)、F2(x)、F3(x)……Fn(x)}。其中,X表示决策变量,Fn(x)表示目标函数。本次实验设计决策变量X就是罗布麻纤维含量,目标函数Fn(x)就是罗布麻/腈纶/莫代尔混纺织物的综合性能。
本文以影响生产加工的耐磨性,与外观息息相关的悬垂性及决定织物保健性能的抗菌性三者为研究目标,建立多目标优化函数。织物的耐磨性越好,经过摩擦前后的质量损失率应当越小,加工过程中越不易断头;织物悬垂性越好其外观效应更好;织物抑菌率愈大,保健性能便愈佳。
将织物耐磨性能看做目标函数F1(x),悬垂性看做目标函数F2(x),抗菌性看做目标函数F3(x)。构成多目标优化函数max{F1(x)、F2(x)、F3(x)}。将实验数据归一化处理,采用Matlab软件Cftool工具箱进行多项式拟合,得到的函数关系表达式如表2所示。表2中置信区间表示的是某个参数的实际值在函数曲线结果范围内的程度,它是一种概率,置信区间值越大,表示函数表达式的可信程度越高[7]。
2.2 加权系数
所谓加权,即是为强调某一要素在整个要素体系中的重要程度而賦予的某一特征值,特征值一般用数值表示,称为这一要素的加权系数[8]。纺织品的设计过程中,根据纺织品的不同用途,其所需的特性也会有所不同。对于内衣型织物,由于其经常与手肘、膝盖摩擦,要求其耐磨性凸出;对于外穿织物,为了追求完美的视觉效果,要求其悬垂性能较好;对于袜子等容易滋生细菌的织物,要求其具备一定的抗菌保健性能。在基于多目标化的纺织品设计中,可以根据纤维间特性的不同,通过调节混纺比来达到纺织品的不同加工需求。
在本实验中,采用层次分析法确定每一类需求的纺织品各性能指标占所有性能指标的权重[9],用wn表示,n=1、2、3,满足0≤wn≤1,且∑3n=1ωn=1。y1表示耐磨性占织物性能的比重,y2表示悬垂性占织物性能的比重,y3表示保健性能占织物性能的比重。根据生产设计经验,加权系数设计值如表3所示。
2.3 混纺比优化计算
线性加权和法,又称“加法”合成法或加权算术平均算子,它是采用线性模型进行综合评价的[10]。利用线性加权和法,通过公式(4),求解各项评价指标值与其对应的权系数的积之和的最大值,其对应的罗布麻纤维含量即是理论最优含量,利用Matlab软件对多目标化函数进行求解。
Y=∑3i=1Fi(x)ωi(4)
式中:Y为织物的综合评价值,Fi(x)为织物的评价指标,wi为织物各项指标的权重系数。
求解得到三种不同设计方案的罗布麻纤维含量依次是20%、29%、50%。因此,当织物要求加工性能优良的时候,其罗布麻理论最优含量应为20%;要求织物外观风格效应好的时候,罗布麻理论最优含量应为29%;要求保健性优良的时候,罗布麻理论最优含量应为50%。本文不讨论莫代尔纤维与腈纶纤维的含量,而将两者视为一个整体,主要考虑罗布麻纤维的含量对织物综合性能的影响。由于实验局限性的存在,目前无法生产出罗布麻纤维含量分别为20%、29%、50%的纱线与织物,所以目前尚不能对理论设计结果进行验证,这将是下一步的研究目标与重点。
运用Matlab软件进行多目标函数模型的建立可以寻找出不同用途时罗布麻纤维的理论最优含量,此最优混纺比可能目前在实际生产过程中开发较困难,但是推进了罗布麻混纺织物的生产研究。同时由于罗布麻纤维长度短,难以成网;其次罗布麻纤维价格昂贵,因此控制罗布麻纤维含量有利于在织物综合性能较好的基础上控制好生产成本,企业在实际应用中可以进行更有针对性的设计生产,提高生产效率,为罗布麻混纺织物的设计与开发提供新的理论性依据。
3 结 论
1)采用灰色聚类分析法发现,罗布麻/腈纶/莫代尔混纺织物的综合性能优于亚麻/棉混纺织物与纯棉织物。
2)基于多目标函数求最优采用线性加权和法是直接从织物的综合性能出发,优选最优的混纺比织物,概念最为清晰,得出的评估结论非常直观。当织物分别要求加工性能优良、外观风格效应良好、保健性优良时,罗布麻纤维理论最优含量分别为20%、29%、50%,为罗布麻混纺织物的生产与开发提供了很好的借鉴作用。
参考文献:
[1]常绍舜.从经典系统论到现代系统论[J].系统科学学报,2011,19(3):1-4.
CHANG Shaoshun. From classical system in the case of modern system theory[J]. Chinese Journal of Systems Science,2011,19(3):1-4.
[2]王永刚,胡开元.一种基于改进灰色聚类分析的综合评价方法[J].中国民航大学学报,2010,28(1):48-51.
WANG Yonggang, HU Kaiyuan. Comprehensive evaluation method based on improved gray-clustering analysis[J]. Journal of Civil Aviation University of China,2010,28(1):48-51.
[3]张罗漫,陈飞,胡琳.综合评价中各指标加权系数确定方法的探讨[J].中国卫生统计,1992,9(3):21-25.
ZHANG Luoman, CHEN Fei, HU Lin. An approach to determing the weighted coefficient of indexes in comprehensive evaluation[J]. Chinese Journal of Health Statistics,1992,9(3):21-25.
[4]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1992:112-114.
DENG Julong. Microbiology[M]. Wuhan: Huazhong University of Science & Technology Press,1992:112-114.
[5]刘思峰,谢乃明.基于改进三角白化权函数的灰评估方法[C]//第16届全国灰色系统学术会议论文集,2008:118-129.
LIU Sifeng, XIE Naiming. A new grey evaluation method based on reformative triangular whitenization weight function[C]//Proceedings of the 16th National Conference on Grey Systems,2008:118-129.
[6]LEUNGA S Y S, WONGA W K, MOK P Y. Multiple-objective genetic optimization of the spatial design for packing and distribution cartoon boxes[J]. Computers & Industrial Engineering,2008,54(4):889-902.
[7]蔣增强,刘明周,赵韩,等.基于多目标优化的产品协同开发任务调度研究[J].农业机械学报,2008,39(3):154-158,162.
JIANG Zengqiang, LIU Mingzhou, ZHAO Han, et al. Task scheduling of product cooperative development based on multi-objective optimization[J]. Transactions of the Chinese Society for Agricultural Machinery,2008,39(3):154-158,162.
[8]李辉芹,巩继贤,黄故.基于MatLab优化工具的混纺织物混纺比设计[J].纺织学报,2009,30(10):62-65.
LI Huiqin, GONG Jixian, HUANG Gu. Design of blending ratio based on Matlab toolbox[J]. Journal of Textile Research,2009,30(10):62-65.
[9]李辉芹,巩继贤,黄故.基于多目标优化的混纺织物设计研究[J].棉纺织技术,2009,37(6):20-23.
LI Huiqin, GONG Jixian, HUANG Gu. Research of blended fabric based on multiple objective optimization[J]. Cotton Textile Techology,2009,37(6):20-23.
[10]孙玮玮,李雷.基于线性加权和法的大坝风险后果综合评价模型[J].中国农村水利水电,2011(7):88-90.
SUN Weiwei, LI Lei. The comprehensive hazard assessment model for the consequences caused by the dam failure based on the linear weighted method[J]. China Rural Water and Hydropower,2011(7):88-90.

