考虑负荷可调节度的年综合峰谷电价模型研究
朱少林 郑仲海 高敏捷 温步瀛
考虑负荷可调节度的年综合峰谷电价模型研究
朱少林1郑仲海1高敏捷1温步瀛2
(1. 国网福建省电力有限公司,福州 350003; 2. 福州大学电气工程与自动化学院,福州 350108)
目前涉及峰谷电价的文献对全年峰谷电价的综合模型缺乏研究,且传统的电价模型仍存在一些不合理的地方,需要继续完善和改进。本文考虑一年4个季度的用电差异性,按各个季度对供电压力的大小来取其权值,提出运用加权二范数对全年的峰谷时段进行划分,从而得到全年综合时段划分方案。提出地区负荷用电可调节度的概念,并将其引入模型作为新的约束条件,提出采用变权重加权法进行多目标优化,建立全年的峰谷电价优化模型。结合某地区实例分析,证明本文模型比已实施的峰谷电价方案具有更好的削峰填谷效果。
峰谷电价;用电差异性;加权二范数函数;负荷可调节度;变权重加权法
近年来,峰谷分时电价制度已在世界各地大范围普及和推行,为缓解电力供应紧张局面作出了巨大贡献[1-3]。峰谷分时电价属于电力需求侧管理范畴,通过有效的激励措施来引导用户减少高峰用电并增加低谷用电,从而优化用电方式和用电结构,提高电网运行可靠性和经济性[4-7]。
峰谷电价的合理制定既要促使负荷曲线平稳化,又要确保各方的经济利益,具有较强的可实施性。峰谷时段的正确划分和峰谷电价调节水平的科学制定非常重要。文献[8-9]利用模糊聚类的方法对时段进行划分。文献[10-11]采用电价弹性矩阵度量用户对峰谷电价的响应,达到了较好的效果[12-15]。
然而,目前的峰谷电价模型研究还存在着一些不足之处,仍有改进的空间。一方面,现行的峰谷电价研究一般都是以某一典型日的负荷曲线作为研究对象,对不同季度的负荷曲线特性缺乏综合考虑。实际上,许多地区峰谷电价的制定通常是以一年为周期,需要对全年的负荷曲线特性进行全面分析。另一方面,传统的峰谷电价模型通常都默认负荷完全可调,没有考虑地区负荷的可调节程度。所以这种假设不太合理,不太符合实际情况。
本文考虑不同季度的用电差异性,采用加权二范数函数[16-17]解决年综合负荷曲线时段划分问题,引入负荷可调节度作为新增约束条件,建立年综合峰谷电价模型。
1 峰谷时段重新划分的方法
根据各季度用电量的比重大小可以确定其权重系数(),即

式中,Q为第季度所选择代表日的总用电量。
本文将各时段对应的负荷看做空间上的点,以负荷最小值和最大值作为定点,计算各点分别到它们间的距离,以空间距离长度作为衡量依据来划分时段。运用二范数可以有效地结合权重系数[18],通过对各个季度负荷用电加权融合,建立全年综合时段划分模型。其中加权二范数函数定义为

(3)
式中,()为第季度时段的负荷功率;a为第季度各时段的最小负荷功率;b为第季度各时段最大负荷功率。
其中,()确定时段处于峰时段的可能性,对()值排序,从数值较高的时间点取起,将最高的16个归为峰时段;()确定时段处于谷时段的可能性,对()值排序,从数值较高的时间点取起,将最高的16个归为谷时段。
2 全年峰谷电价数学模型
本文提出的全年峰谷电价模型是建立在基于用户响应的峰谷电价模型的基础上,通过考虑季节用电差异性,提出峰谷电价的全年综合定价方法。该模型基本假设是,调整峰谷电价前后典型日的用电总量保持不变。
1)峰谷电价目标函数
执行峰谷分时电价制度的主要目的是减小负荷曲线的最大峰值和峰谷差值,起到削峰填谷、平稳负荷曲线的作用。以最小化负荷曲线最大峰负荷和峰谷差为目标,采用自适应变权重加权法进行多目标优化,结合权重系数后,构造全年峰谷电价模型的优化目标函数为

式中,Q为第季度典型日各时段的平均负荷电量;max()为第季度典型日各时段负荷电量中的最大负荷电量;min()为第季度典型日各时段负荷电量中的最小负荷电量;1()、2()分别为第季度的两个优化目标;1()、2()为第季度的变权重系数;(Q)为第季度的目标函数;min(D)为全年的综合优化目标函数。
式(4)作为全年峰谷电价模型的目标函数需要考虑内外两层的权重,外层的权重系数由各季度在全年的用电比重决定,内层的权重系数由每季度各自典型日的峰谷差和平均负荷电量所决定。
2)传统约束条件
为保证峰谷分时电价制度能持续、有效地执行,应确保实施峰谷电价后电力的供需双方均受益或者均不受损害。目前峰谷分时电价模型的约束条件主要从电网公司收益、用户收益和边际成本3个方面来考虑。
(1)用户的收益约束
用户进行峰谷电价调整后的电费支出应该小于或等于峰谷电价调整前的电费支出。
(2)电网公司的收益约束
实施峰谷电价可以减少电网投资,假设执行峰谷电价电网公司节省的成本为w,则电网公司的收益约束为

式中,so为峰谷电价调整前电网公司的收入;s为调整后电网公司的收入。
(3)边际成本约束
为保证电网成本的合理回收,低谷电价水平应不低于电网谷时段的边际成本。
3)新增约束条件
传统的峰谷电价模型通常默认实施地区的负荷用电都可以进行调节,这种假设显然过于理想。实际上,不是所有执行对象都可以或愿意实施峰谷电价制度,如钢铁厂普遍全天候运作,实行峰谷分时电价制度对其改善用电方式的作用有限。所以,本文以可调节度作为新增约束条件来限制执行峰谷电价的有效对象,提高模型的准确性。
一个地区负荷用电的可调节度与该地区的气候、产业结构、居民用电习惯等诸多因素有关。可以对地区用电情况进行调研,通过统计各类大用电客户的用电量和用电方式来评估该地区负荷用电的可调节度。可调节度越大,表明执行峰谷分时电价的有效对象越多,有利于峰谷分时电价制度的实施。若用表示最大可调节度,则可调节度约束的表达式为

式中,max、min分别为调整后典型日各时段的最大和最小负荷电量;、分别为调整前典型日各时段的最大和最小负荷电量;为典型日各时段的平均负荷电量。
3 算例分析
3.1 峰谷时段的划分
某地区已执行峰谷电价政策多年,近年来实施的时段划分方案见表1。

表1 峰谷时段划分
该地区2015年各个季度的典型日负荷曲线如图1所示。数据以30min为截取点,一日为48个点。
全年的综合负荷曲线需要兼顾4个季度的用电差异,以权重系数()表示各季度用电量占全年总用电量的比重。经过计算可得4个季度的权重系数见表2。

图1 各个季度典型日的负荷功率曲线

表2 权重系数
通过对各个季度典型日相应电量进行加权分析,可得整年综合典型日负荷功率曲线如图2所示。

图2 整年综合典型日负荷功率曲线
利用式(2)和式(3)可以得到各时间点处于高峰时段和低谷时段的隶属度值,见表3。
初步判断后结合已实施方案特点进行适当调整,得到重新划分结果见表4。选取了48点数据计算,得到的时段划分结果以半小时为单位。
研究表明,该地区用电时段特性与历史对照发生了较大的改变[18]。
3.2 全年峰谷电价调整
由于该省已实施峰谷电价多年,所以现存的可调负荷很有限,构建峰谷电价的调整优化模型时,可调节度不宜设置得过大。
若设该省现存的可调负荷占地区总负荷的9%,则设置可调节度=0.1。取该省已实施方案的平时段电价作为本文方案的平时段电价,在约束条件下,以最小化负荷曲线最大峰负荷和峰谷差为目标进行优化,通过仿真计算可以得到全年综合峰谷电价调整方案,即峰时段电价在平时段电价的基础上上调45.37%,谷时段电价在平时段电价的基础上下调43.29%。
以该年综合峰谷电价调整结果进行负荷电量预测,得到调整前后4个季度的典型日负荷曲线如图3—图6所示。

表3 各时段的峰/谷隶属度值

表4 峰谷时段划分结果
从调整前后4个季度的典型日负荷曲线图可以看出,可调节度设置为9%的改进模型对负荷曲线形状的改善效果不错。根据模型计算结果显示:峰谷电价调整后至少可以减少峰谷差约7.5%,最多可以减少近10%的峰谷差,使得负荷用电更趋于平稳。

图3 第一季度典型日负荷曲线

图4 第二季度典型日负荷曲线

图5 第三季度典型日负荷曲线
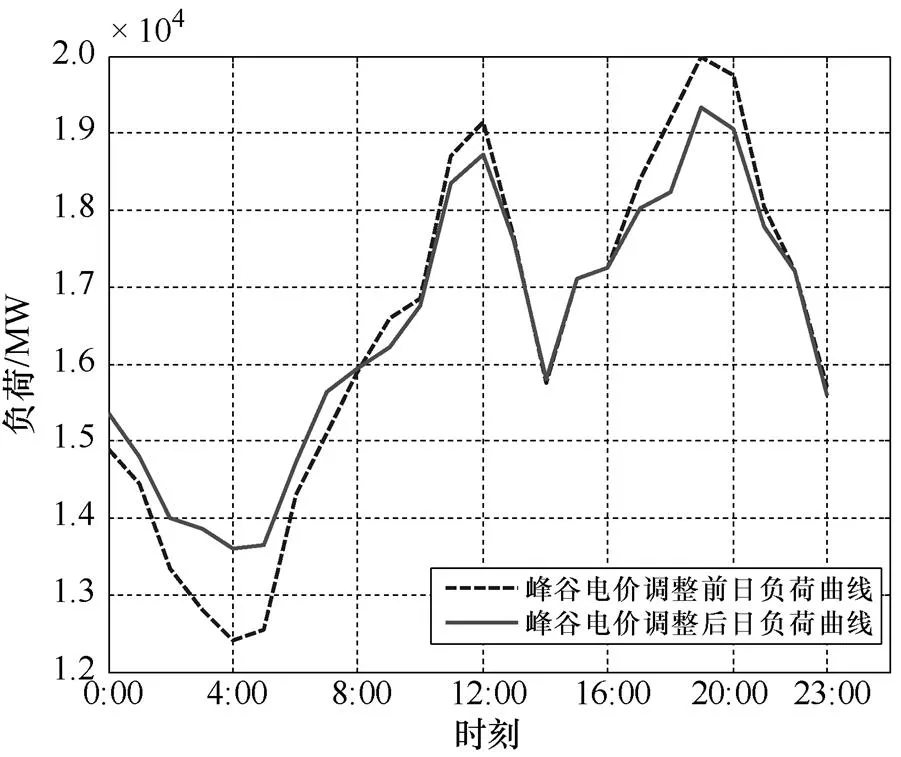
图6 第四个季度典型日的负荷特性曲线
4 结论
本文考虑4个季度的用电差异性,利用加权二范数函数法,对某地区的4个季度的典型日负荷曲线进行峰谷时段划分,得到年综合时段划分方案。
在此划分基础上,考虑地区负荷用电的可调整程度,提出引入负荷可调节度作为峰谷电价模型新增约束条件,并采用变权重加权法构建新的目标函数。按各个季度对供电压力的大小来取其权值进行年度综合调价,得到全年的峰谷电价调整方案。与已实施峰谷电价方案相比,本文模型可以更好地引导用电用户削峰填谷,效果更佳,可以一定程度地改善负荷曲线的形状。
[1] 李昌. 基于分时电价的办公建筑中央空调最优起动时间计算[J]. 电气技术, 2015, 16(8): 34-39.
[2] 赵娟, 谭忠富, 李强. 我国峰谷分时电价的状况分析[J]. 现代电力, 2005, 22(2): 82-85.
[3] 翁桂萍, 潘夏, 邵振国. 计及峰谷电价和启发式运行策略的风光储联合发电用户容量优化[J]. 电气技术, 2016, 17(5): 1-6.
[4] 别朝红, 李更丰, 谢海鹏. 计及负荷与储能装置协调优化的微网可靠性评估[J]. 电工技术学报, 2014(2): 64-73.
[5] Roos J G, Lane I E. Industrial power demand response analysis for one-part real-time pricing[J]. IEEE Trans on Power Systems, 1998, 13(1): 159-1641.
[6] Kirschen D S. Demand-side view of electricity markets[J]. IEEE Transactions on Power Systems, 2003, 18(2): 520-527.
[7] 茆美琴, 金鹏, 张榴晨, 等. 工业用光伏微网运行策略优化与经济性分析[J]. 电工技术学报, 2014, 29(2): 35-45.
[8] 丁宁, 吴军基, 邹云. 基于DSM的峰谷时段划分及分时电价研究[J]. 电力系统自动化, 2001, 25(23): 9-12, 16.
[9] 程瑜, 翟娜娜. 基于用户响应的分时电价时段划分[J]. 电力系统自动化, 2012, 36(9): 42-46, 53.
[10] Sheen J N, Chen C S, Wang T Y. Response of large industrial customers to electricity pricing by voluntary time-of-use in Taiwan[J]. IEE Proceedings-Generation, Transmission and Distribution, 1995, 142(2): 157-166.
[11] 秦祯芳, 岳顺民, 余贻鑫, 等. 零售端电力市场中的电量电价弹性矩阵[J]. 电力系统自动化, 2004, 28(5): 16-19, 24.
[12] 郑成, 田宇, 陈一怀. 基于模糊聚类的峰谷时段划分[J]. 电气技术, 2016, 17(6): 13-17.
[13] 郭联哲, 谭忠富, 李晓军. 基于用户响应下的分时电价优化设计模型与方法[J]. 电网技术, 2006, 30(5): 24-28.
[14] 项顶, 宋永华, 胡泽春, 等. 电动汽车参与V2G的最优峰谷电价研究[J]. 中国电机工程学报, 2013, 33(31): 15-25.
[15] 孙近文, 万云飞, 郑培文, 等. 基于需求侧管理的电动汽车有序充放电策略[J]. 电工技术学报, 2014, 29(8): 64-69.
[16] Auscher P, Martell J M. Weighted norm inequalities, off-diagonal estimates and ellipticoperators[J]. Part II: Off-diagonal Estimates on Spaces of Homogeneous Type. J. Evol. Equ, 2007, 7(2): 265-316.
[17] Auscher P, Martell J M. Weighted norm inequalities, off-diagonal estimates and ellipticoperators[J]. Part I: General Operator Theory and Weights. Adv. Math, 2007, 212(1): 225-276.
[18] 连振洲, 温步瀛, 江岳文. 基于负荷曲线分布特征的峰谷时段划分和修正策略研究[J]. 电网与清洁能源, 2014(7): 15-19.
Annual Comprehensive Peak-valley Price Model Considering the Load Adjustable Degree
Zhu Shaolin1Zheng Zhonghai1Gao Minjie1Wen Buying2
(1. State Grid Fujian Electric Power Company, Fuzhou 350003; 2. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108)
Currently, the literature on peak-valley price is lack of research on the annual comprehensive model of TOU. In consideration of the differences between the four quarters of electricity service condition, according to the electricity amount of each quarter to take the weight, using a weighted two-norm function method to divided peak-valley time periods of the year. This paper considers regional electricity load adjustable, taking it as a new constraints of the new mode. The year’s peak-valley price model uses the adaptive variable weight weighting method to solve the multi-objective problem.Through the study of the cases of a certain area to prove that the model has better peak effect than the peak-valley price scheme has been implemented.
peak-valley price; the difference of electricity; weighted two-norm function; load adjustable degree; variable-weight weighting method
朱少林(1979-),男,福建泰宁人,硕士,高级工程师,主要研究方向为电力市场。

