基于超级电容储能的船舶电力推进系统鲁棒控制策略
张大闯,王锡淮,肖健梅
基于超级电容储能的船舶电力推进系统鲁棒控制策略
张大闯,王锡淮,肖健梅
(上海海事大学,上海201306)
在船舶电力推进系统中加入超级电容储能装置,能够实现对电网电能的回馈与吸收,从而使整个电网运行于最佳状态。因此如何实现对同步发电机及超级电容的控制关系到整个电网的质量。本文运用鲁棒控制理论设计出H∞混合灵敏度控制器对同步发电机及超级电容进行跟踪控制,然后在simulink中建立模型来验证所设计控制器的控制效果。结果表明,所设计控制器能够实现很好的跟踪效果。
超级电容 同步发电机 H∞控制 鲁棒控制
0 引言
解决船舶电力系统的不确定性和非线性问题,是控制理论应用于实际电力系统的重要问题。大量的不确定性因素,如各种故障的发生,设备和负荷的随即投切等,都可视为对控制系统的某种扰动,它们会影响发电机的端电压的变化。鲁棒控制理论能够很好地解决上述不确定性因素的影响[1]。控制界将H∞鲁棒控制理论的发展过程分为两个阶段,分别以加拿大学者Zames[3]和美国学者Doyle[4]等人发表的两篇著名论文为标志。称前一阶段的理论为经典H∞鲁棒控制理论,称后一阶段的理论为状态空间H∞鲁棒控制理论[2]。在文献[5]中提出了一种改进的显模型跟踪H∞回路成形控制方法,利用H∞回路成形算法补偿显模型跟踪算法中前馈模型逆的不确定性。文献[6]运用μ综合方法提出了一种收敛性更强的“隐式欧拉加外推”算法。通过对比平衡截断法和Hankel范数逼近法对控制器进行降阶优化处理,对比降阶效果进行偏差估计,分析降阶前后与降阶方法差异导致的闭环系统鲁棒性。本文将运用鲁棒控制理论中H∞混合灵敏度优化方法,对具有不确定性的发电机及超级电容进行控制,以达到跟踪所给参考电压的目的。
1 系统建模
同步发电机及超级电容的控制框图如图1所示,下面就各个模块的建模做如下介绍。
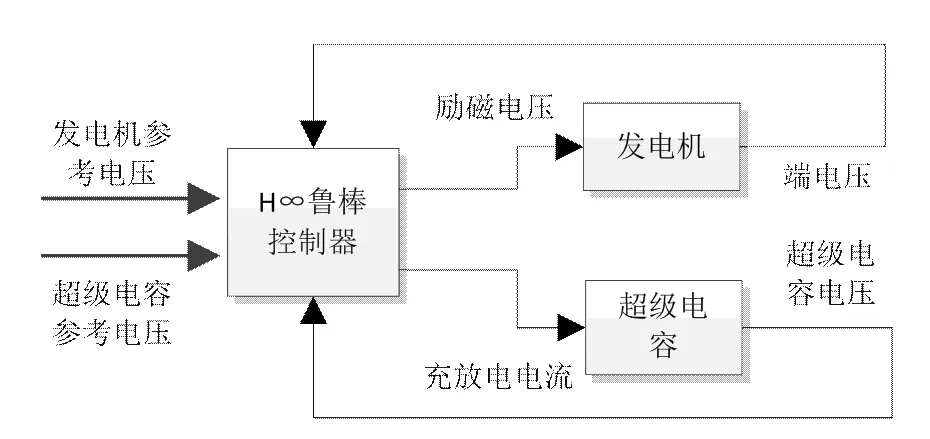
图1 控制框图
1.1发电机励磁模型
同步发电机将原动机的热能转化为电能,供给船舶电力系统,是船舶电力系统的核心。建立合适的数学模型,对整个船舶电力系统的动态特性分析至关重要。通过对发电机励磁进行控制,目前被认为是提高电力系统稳定性较为经济、可靠的方法。本文利用磁链及电压平衡方程在同步电机dq0坐标系通过帕克变换建立了以v、i、i为输入量,i、v、v为输出量的三阶状态方程[7-9]:
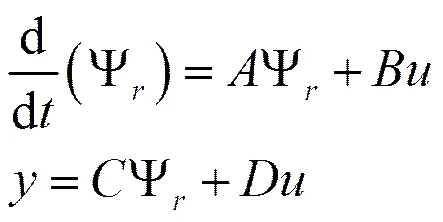
其中

采用H∞控制器的交流无刷励磁控制系统框图如图2所示:

图2 H∞交流无刷励磁控制系统框图
从图2可以看出,控制信号是通过交流励磁机及旋转整流器转换为励磁电压E的,其传递函数满足式
其中,代表励磁机的积分常数,取值为2.198,为增益,取值为8.9,则可由上式推得其微分方程如下
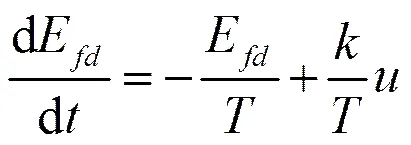
联立(1)、(2)推得交流无刷励磁系统的状态空间方程如下式:
其中
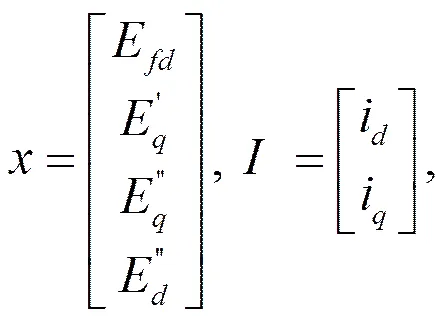
1.2超级电容模型
超级电容器是船舶储能系统关键部分,且成本也非常高[10],鉴于此,超级电容的模型结构应尽量简单,超级电容都是由电阻、电容的串并联而成,经典的超级电容模型如图3所示,它结构简单且最实用。
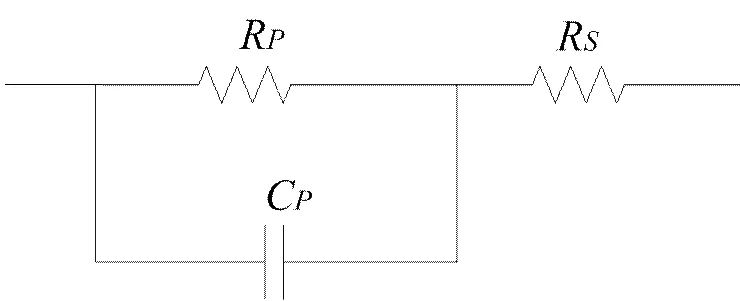
图3 经典模型
超级电容的等效电气模型如图4所示:
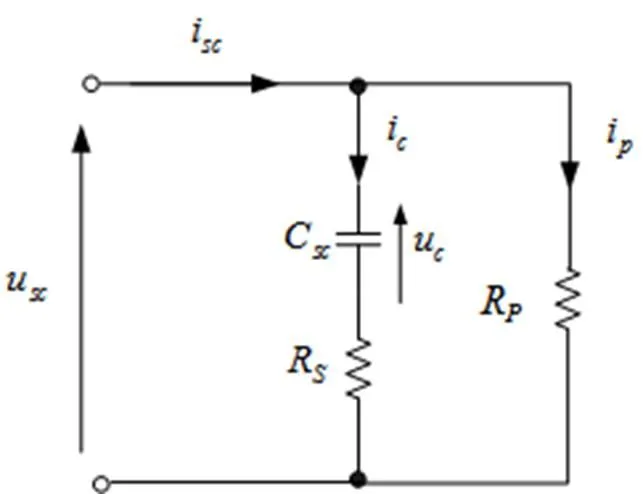
图4 超级电容等效电路图
由基尔霍夫电压电流关系可得:

以u为状态变量,i为控制变量,u为输出变量,可得该模型的状态空间方程为:
其中

2 H∞混合灵敏度鲁棒控制器
为了使发电机及超级电容拥有足够的干扰抑制和信号跟踪能力,采用H∞混合灵敏度控制方法。它采用的是一种迂回策略,即不去具体研究在各种显式的作用下H∞控制器的设计方法,而是把的影响换成某种加权函数,从而给优化问题带来很大的灵活性。H∞控制的混合灵敏度优化方法原理框图如图5:
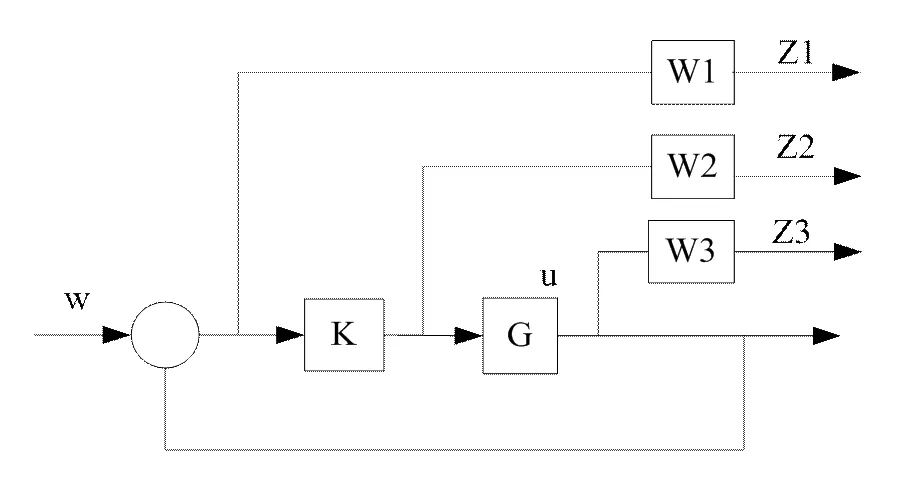
图5 H∞混合灵敏度鲁棒控制框图
引入灵敏度函数及补灵敏度函数如下:
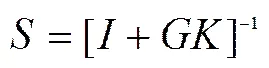

求解H∞控制器就是寻找一个控制律K满足
鲁棒控制器设计的关键是在于加权函数的选取,往往需要多次尝试才能选择好合适的加权函数,在这里同步发电机的加权函数选为:
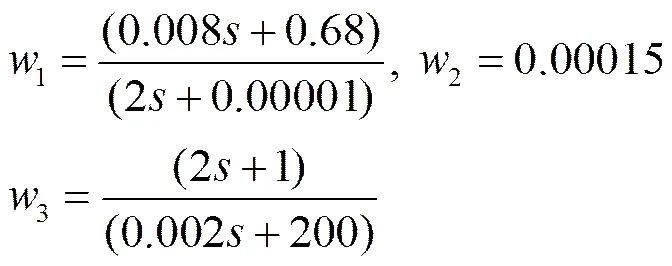
超级电容的加权函数选为:
所设计的同步发电机及超级电容的控制器分别为:
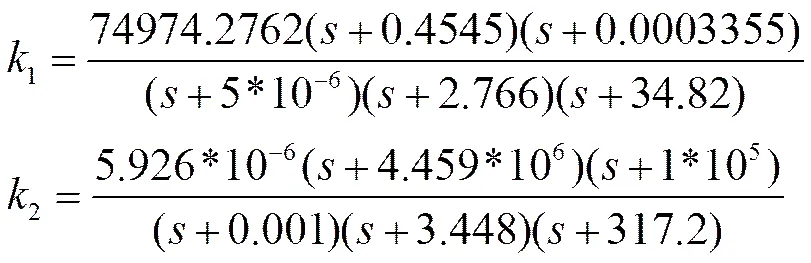
3 仿真与分析
根据以上分析,为验证本文方法的有效性,利用Matlab/Simulink建立了仿真模型。
同步发电机主要参数如表1:
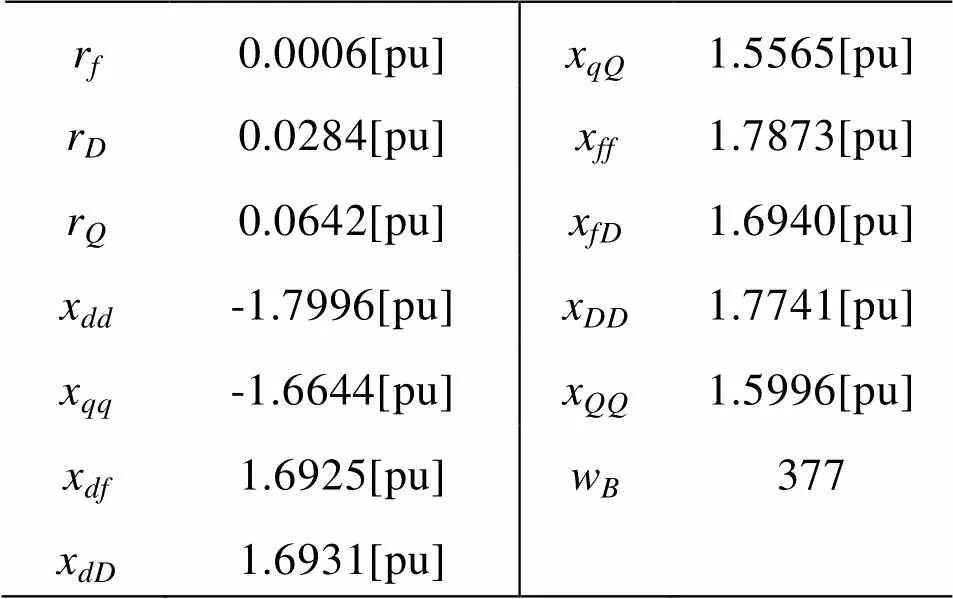
表1 同步发电机主要参数
本文所用到的超级电容为法国电力公司和BOLLORE集团合资生产。其详细参数为:超级电容并联电阻p=200 Ω;超级电容串联电阻R=3 mΩ;超级电容电容C=375 F;超级电容额定电压=65 V。
仿真结果如下:
图6为发电机系统灵敏度函数及其加权函数的奇异值曲线,因为W1与S的乘积反映了系统的性能,所以必须满足,由图6可以看出,符合设计要求。
图7为发电机补灵敏度函数T与W3的奇异值曲线,因为T与W3的乘积表示系统的鲁棒性要求,应满足,由图7可以看出,,可以满足系统鲁棒稳定性的要求。
同理超级电容灵敏度函数及其加权函数的奇异值曲线、补灵敏度函数T与W3的奇异值曲线分别如图8、9所示,从图中可以看出也达到了与发电机相似的设计效果,在这里不再赘述。
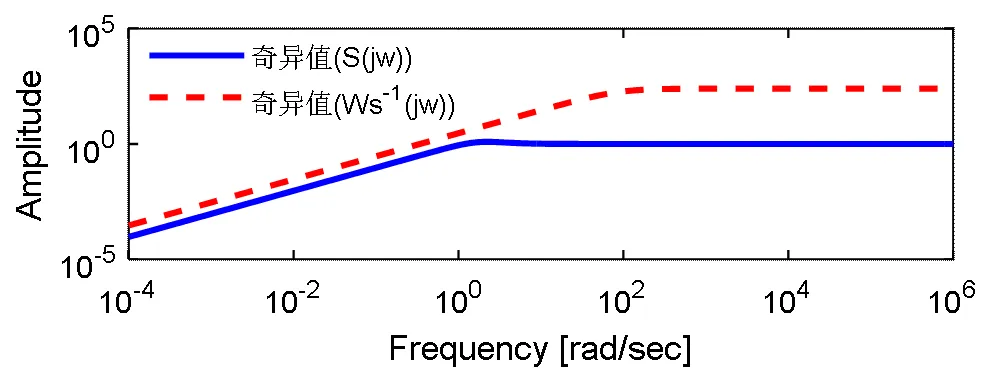
图6 发电机灵敏度及其加权函数奇异值曲线
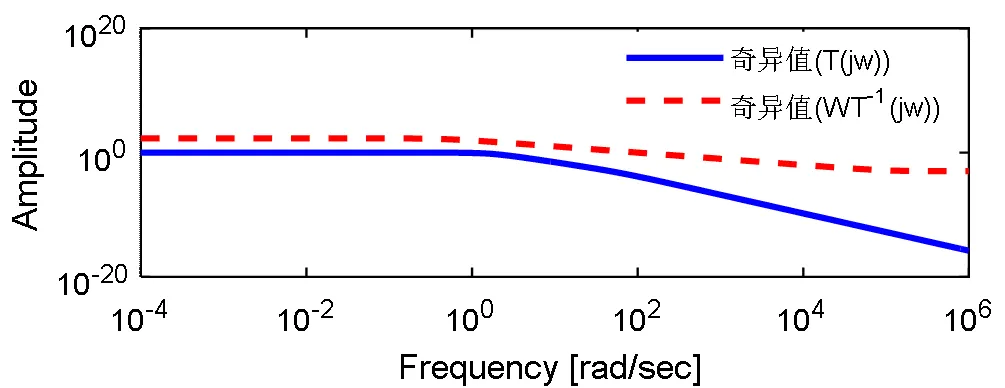
图7 发电机补灵敏度及其加权函数奇异值曲线
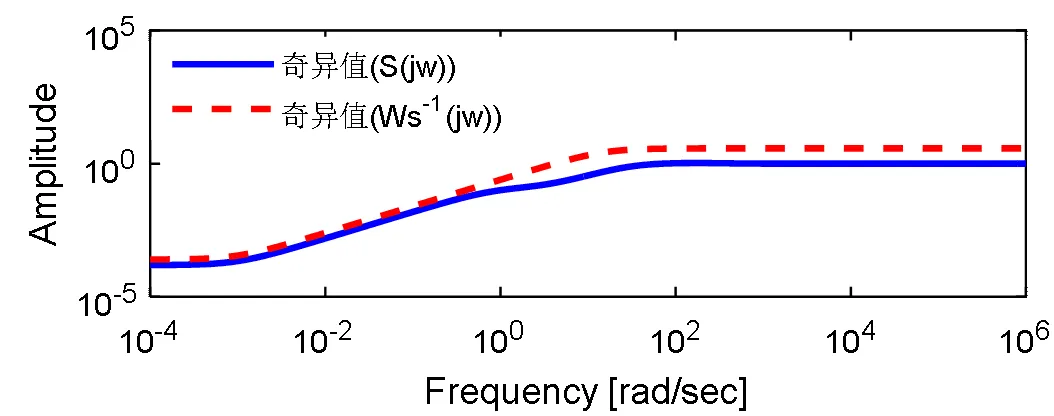
图8 超级电容灵敏度及其加权函数奇异值曲线
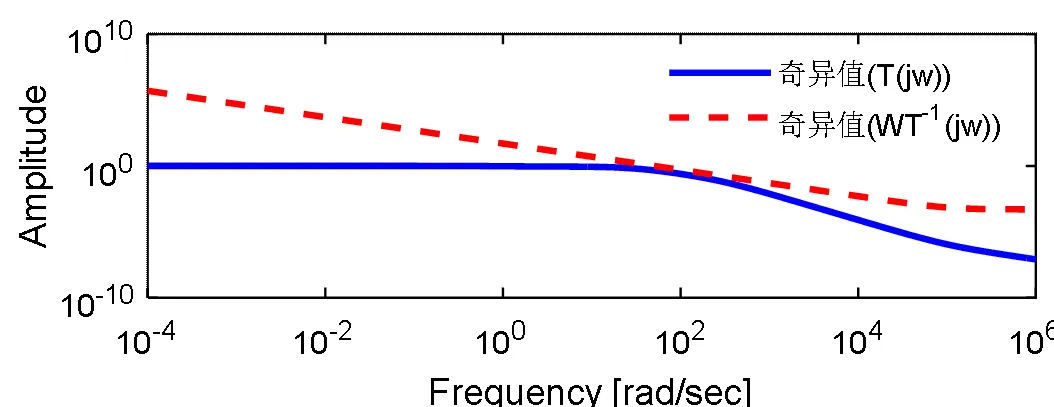
图9 超级电容补灵敏度及其加权函数奇异值曲线
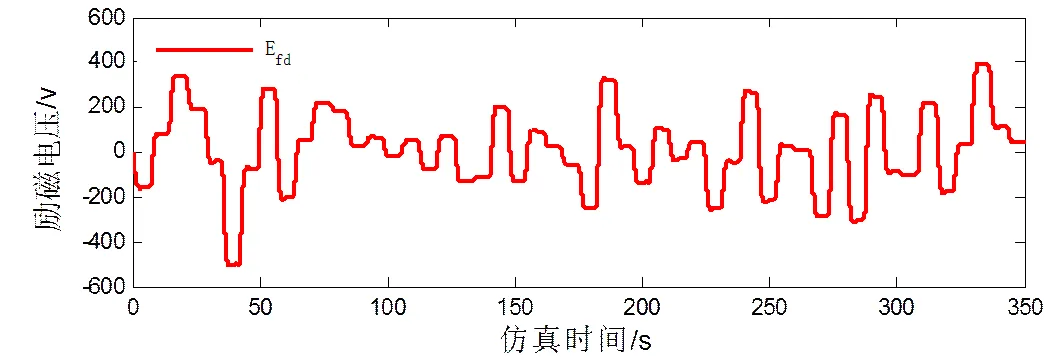
图10 发电机励磁电压曲线

图11 超级电容充放电电流曲线
发电机励磁电压曲线、超级电容充放电电流曲线如图10、11所示,发电机及超级电容的电压跟踪曲线如图12、13所示。从图中可以看出,通过对发电机励磁电压及超级电容充放电电流进行控制可以实现对给定参考电压的跟踪,且跟踪效果良好。
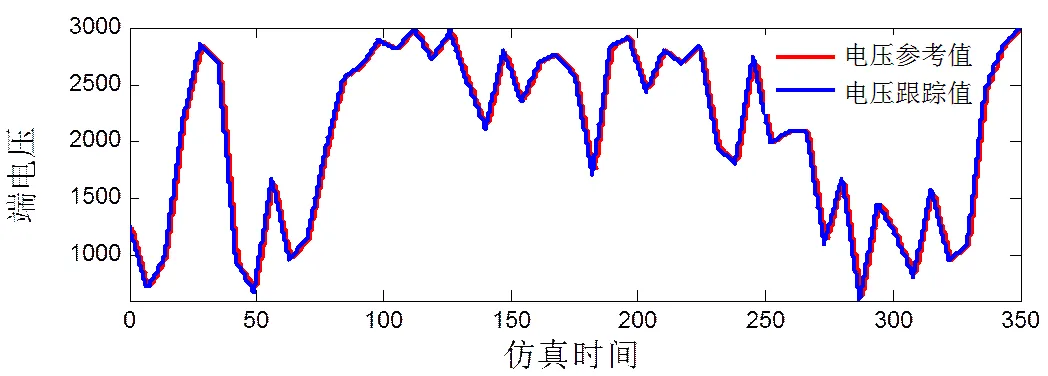
图12 发电机电压跟踪曲线
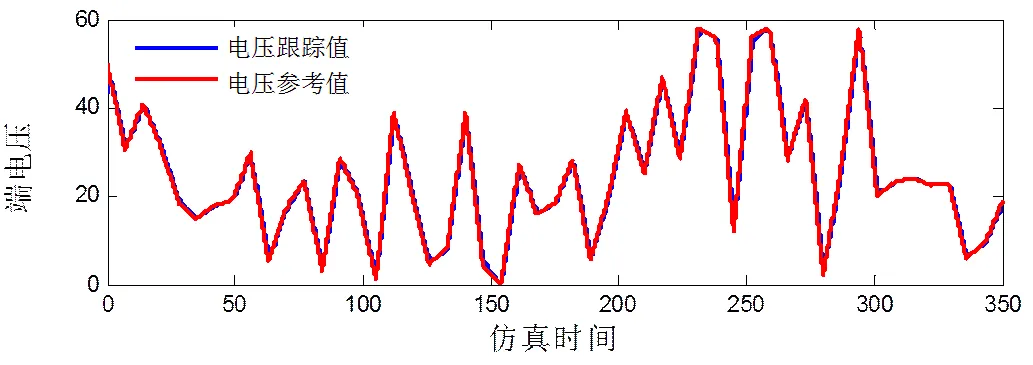
图13 超级电容电压跟踪曲线
3 结论
含超级电容储能的电力系统中,超级电容要缓和负载的高频波动,从而保证发电机在负载发生变化时只有很小的波动,因此可控制其充放电电流来实现对电网电能的回馈与吸收,通过以上分析,可以看出所设计的控制器能够实现很好的跟踪给定电压参考值,以满足负载的变化。
[1] 张敏, 罗安, 王华昕. 基于线性化的发电机励磁鲁棒控制器[J]. 电工技术学报, 2002(17): 85-87.
[2] 张显库. H∞鲁棒控制理论发展的十年回顾[J]. 控制与决策, 1999(14): 289-296.
[3] Zames G.. Feedback and optimal sensitivity: Model reference transformations, multiplicative seminorms and approximate inverses. IEEE T ran s AC, 1981, 26( 4) : 301- 320.
[4] Doyle J C, K Glover, P P Khargonekar. Stat e- space solution s to standard H2 and H∞ control problems. In : ACC′88. Atlanta, 1988. 817- 823.
[5] 王晓燕. 基于MOGA算法的H_回路成形直升机姿态控制器设计[J]. 控制与决策, 2016, (1): 59-65.
[6] 臧月进. 空-空导弹μ综合控制降阶与算法[J]. 兵工自动化, 2011,(30): 5-8.
[7] Tommy Andy Theubou Tameghe.’ Modélisation et Simulation d'un Système de Jumelage éolien-diesel Alimentant Une Charge Locale’, Université du québec.2012.8: 85-90, 93-108.
[8] RenÉ Wamkeue ; Frederic Baetscher ; Innocent Kamwa, “Hybrid-State-Model-Based Time-Domain Identification of Synchronous Machine Parameters From Saturated Load Rejection Test Records”, IEEE Journals &Magazines, 2008 (23): 68-77.
[9] 刘勇智, 刘聪. 基于状态空间法的航空同步发电机建模方法研究[J]. 微电机, 2011,(44): 48-51.
[10] S.Trieste, S.Hmam, J. -C. Olivier, S. Bourguet, L. Loron’ Techno-economic optimization of a supercapacitor-based energy storage unit chain: Application on the first quick charge plug-in ferry’, Applied Energy, 153 (2015): 3–14.
Robust Control Strategy of Ship Electric Propulsion System Based on Supercapacitor Energy Storage
Zhang Dachuang, Wang Xihuai, Xiao Jianmei
(Shanghai Maritime University, Shanghai 201306, China)
N945.12
A
1003-4862(2017)08-0028-05
2017-04-14
张大闯(1991-),男,硕士研究生。研究方向:复杂系统控制与优化。Email: 1369104602@qq.com

