基于悬臂板扭转模态测试材料剪切模量
王 正 曹 瑜 王韵璐 李敏敏
(南京林业大学材料科学与工程学院 南京 210037)
基于悬臂板扭转模态测试材料剪切模量
王 正 曹 瑜 王韵璐 李敏敏
(南京林业大学材料科学与工程学院 南京 210037)
【目的】 探讨基于悬臂板扭转模态测试正交各向异性材料(木材)和各向同性材料剪切模量的原理和方法。【方法】 首先根据ANSYS计算的悬臂板一阶扭转振形,应用优化原理分别得到垂直和平行于板中面位移w和u的一阶扭转振形函数,然后借助能量法导出悬臂板一阶扭转频率与板材弹性模量和剪切模量的关系式,该式中的2个振形系数通过与动能、扭转应变能和拉压应变能相关积分计算,从振形系数计算值的二元线性回归得到振形系数依赖于悬臂板宽长比和厚宽比的相关式。【结果】 导出的悬臂板一阶扭转频率与板材弹性模量和剪切模量的关系式,只有在测出悬臂板一阶弯曲频率得到弹性模量后,才能应用这个关系式由悬臂板一阶扭转频率推算出剪切模量。【结论】 导出了悬臂板一阶扭转频率与弹性模量和剪切模量之间的关系式,其中振形系数依赖于悬臂板宽长比和厚宽比。该关系式动态测试剪切模量的正确性不仅得到低碳钢、轧制铝、桃花心木、白蜡木和轻木剪切模量仿真计算的验证,还得到低碳钢、西加云杉(径切面和横切面)、蒙古栎(顺纹)和油松(弦切面和径切面)等材料剪切模量的动态和静态试验的验证,且基于悬臂板一阶扭转模态与自由板扭转振形法测试木材或各向同性材料的剪切模量相当吻合。基于悬臂板一阶扭转模态提供了一个应用悬臂板频谱动态测试剪切模量的简便和快速的方法,该方法不仅适用于测试木材的3个主向剪切模量GLT、GLR和GRT,还适用于测试各向同性材料的剪切模量。
悬臂板; 扭转振形系数; 动态测试; 剪切模量
Abstract: 【Objective】 The principle and method of testing shear modulus of orthotropic materials(wood)and isotropic materials based on the torsional mode of cantilever plate are discussed.【Method】 Firstly, based on the first-order torsional vibration shapes of the cantilever plate according to the ANSYS calculation, the first-order torsional vibration shape function of the displacementwandu, which are perpendicular and parallel to the middle of the plane respectively,are obtained by applying optimization principle. Then, the energy method is used to derive the relational expressions between the first-order torsional frequency and elastic/shear modulus of the cantilever plate, the two vibration shape coefficients are calculated through the integral related with kinetic energy, torsion/tension/compression strain energy, and the binary linear regression of the calculated value of the vibration shape coefficient depends on related expressions of the width-to-length ratio and thickness-to-width ratio.【Result】 The relational expressions derived between the first-order torsion frequency and elastic/shear modulus of the cantilever plate, it can be used to calculate shear modulus by the first-order torsional frequency only after obtaining elastic modulus through measuring the first-order bending frequency of the cantilever plate.【Conclusion】 The relationship between the first-order torsional frequency and the elastic/shear modulus of the cantilever plate is derived, and the vibration shape coefficient is dependent on the width-to-length ratio and the thickness-to-width ratio. The correctness of relational expressions are verified not only by the dynamic shear modulus determined from low carbon steel, rolling aluminum,Swieteniamahagoni,FraxinusamericanaandOchromapyramidale, but also by the dynamic and static shear modulus tested from low carbon steel,Piceasitchensis(radial section and transverse section),Quercusmongolica(parallel to grain),Pinustabulaeformis(tangential section and radial section)and so on. Based on the first-order torsional mode of the cantilever plate and the torsional vibration shape method of the free plate, shear modulus of wood or isotropic materials are in good agreement. The first-order torsional mode based on the cantilever plate provides a simple and rapid method to determine the dynamic shear modulus using cantilever plate. This method can be used not only to test wood shear modulusGLT,GLRandGRTin the three main directions, but also be applied in testing shear modulus of isotropic materials.
Keywords: cantilever plate; torsional vibration shape coefficient; dynamic test; shear modulus
弹性模量是材料特性的基本参数之一, 北美产的成材上均标有弹性模量值,木材加工业中实现了通过成材的弹性模量值导出其成材强度指标的目标。早期曾用连续测试机装置测试成材的弹性模量, 但由于连续测试机需要巨额投资, 显然不能成为合适的测试成材弹性模量设备。20世纪80年代以来,国内应用无损检测的应力波法和动态振动法测试成材的弹性模量(王志同, 1991; 王志同等, 1995; 刘镇波等, 2005; 张厚江等, 2005; 王正, 2007; 王正等, 2013; 2015),其中,动态振动法因具有快速、简便、重复性好等优点,被广泛应用于刨花板、密度纤维板等准各向同性材料以及木材弹性模量值的动态测试。实际上,剪切模量也是材料特性的基本参数之一, 反映了材料或构件的抗剪切能力,已应用于新一代重型木结构交错层积材(CLT)的刚度、强度计算和设计中(Gulzowetal., 2011)。但由于剪切模量动态测试的原理高深,技术困难,使得木材和木质复合材料剪切模量动态测试的进展速度较为缓慢,在此方面所发表的文献也较少。胡英成等(2001a)应用应力法测试了刨花板、胶合板的剪切模量; 胡英成等(2001b)采用考虑剪力和梁截面的回转效应对梁弯曲频率影响的TGH法测试了胶合板的剪切模量。周海宾等(2007a)考虑剪力和回转惯性对自由梁自振频率的影响, 在一阶和二阶自振弯曲频率中包含弹性模量E和剪切模量G2个弹性常数, 采用迭代方法得到了剪切模量G; 周海宾等(2007b)引用一个悬臂矩形杆件扭转振动方程,并通过检测悬臂杆件的一阶扭转频率推算出了木质复合板的剪切模量G。王正等(2014)和程可等(2015)分别用自由板扭转振形法测试了木材和各向同性材料的剪切模量,其正确性得到剪切模量仿真计算、动态试验和静态试验3方面的验证,但其采用自由板为试件测试各向同性材料和木材剪切模量的方法,是不同于用悬臂梁或悬臂板为试件测试刨花板和胶合板等木质复合材料剪切模量的。
木材加工业中对弹性模量和剪切模量的测试通常采用悬臂梁作为试件,因此本文以悬臂板为试件,提出了另一种动态测试木材和各向同性材料剪切模量的方法。悬臂板的扭转不像自由板,属于约束扭转, 即扭转时横截面上不但存在扭转剪应力, 还存在拉伸或压缩正应力。从能量角度来说, 当悬臂板扭转时, 不仅要考虑动能和扭转应变能, 还要考虑与横截面上拉(压)正应力相应的拉(压)应变能,因此应用能量法导出的是剪切模量与悬臂板一阶扭转频率和弹性模量的耦合关系式,只有在确定了材料的弹性模量后,才能应用这个耦合关系式从悬臂板的一阶扭转频率测试值推算出剪切模量。但幸运的是,较易用材料的悬臂板一阶弯曲频率值推算得到其弹性模量。用悬臂板测试剪切模量, 引入了2个振形系数,其中一个振形系数C1与悬臂板作一阶扭转振动时的扭转应变能和动能比值有关,另一个振形系数C2与悬臂板作一阶扭转振动时的拉(压)应变能和扭转应变能比值有关。若只用与振形系数C1相关项的计算值估计其剪切模量,会过高地估计剪切模量,要得到正确的剪切模量测试值必须要用与C1相关项的计算值减去与C2相关项的计算值。当以长宽比等于1或2的悬臂板为试件测试剪切模量时,必须计入与C2相关项。本文的特色之一是引入振形系数C2,从而保证了通过悬臂板试件一阶扭转频率测试值推算其剪切模量的正确性。文中,通过悬臂板扭转模态方法测试材料剪切模量的正确性得到了静态方板扭转试验和剪切模量仿真计算的验证。此外,还比较了同一材料、同一试件用自由板扭转振形法(王正等, 2014; 2016)和基于悬臂板扭转模态法所测试的剪切模量。基于悬臂板扭转模态测试剪切模量是一个应用悬臂板频谱简便、快速测试剪切模量的方法,适用于测试各向同性材料和正交各向异性的木材剪切模量。
1 剪切模量与悬臂板一阶扭转频率关系
1.1悬臂板的一阶扭转振形函数
设悬臂板长为l(x向), 宽为b(y向), 厚为h(z向), 见图1。

图1 悬臂板坐标系Fig.1 Cantilever plate coordinates
悬臂板一阶扭转振动的z向位移w(x,y,t)=W(x,y)sinωt, 其中振形函数W(x,y)可表示为:
W(x,y)=A(x+B/Ax2/l+C/Ax3/l2+

或用角点位移W(l,b/2)表示为:
W(x,y)=kwW(l,b/2)(x+awx2/l+bwx3/l2+

kw按x=l、y=b/2的W(x,y)=W(l,b/2)决定。在模态分析时若采用单位长度归一, 即W(l,b/2)=1, 则kw=A。系数aw、bw、cw和dw由优化原理和悬臂板振形沿其长边z向分量w确定。
截面扭转角为:
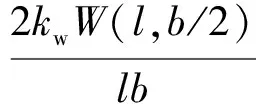
cwx4/l3+dwx5/l4)sinωt。
悬臂板扭转属约束扭转, 矩形横截面上除扭转剪应力外,还存在正应力。正应力与悬臂板x向位移u有关。考虑x向位移u沿板厚度的变化,根据计算的振形,杆件一阶扭转模态的轴向位移u相应的振形函数U(x,y,z)可表示为:
u(x,y,z,t)=U(x,y,z)sinωt
U(x,y,z)=kuU(l,b/2,h/2)(x+aux2/l+

ku按x=l、y=b/2、z=h/2的U(x,y,z)=U(l,b/2,h/2)决定,ku=1/(1+au+bu+cu+du)。系数au、bu、cu和du由优化原理和悬臂板振形沿其长边x向(轴向)分量u确定。
1.2动能
;

1.3应变能

1.3.2 拉压应变能 考虑矩形截面杆件扭转时与截面上正应力相关的应变能(Uσ)max:
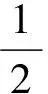
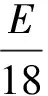

根据Tmax=(Uφ)max+(Uσ)max, 有
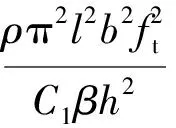
(1)
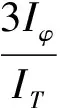
式(1)右边第1项是未计入正应力影响、仅考虑扭转剪应力时推算G的关系式(为今后叙述方便, 其推算值称为Guncorrected), 第2项是计入正应力影响的修正项(其计算值称为Gcorrected),G=Guncorrected-Gcorrected。由于悬臂板在扭转时截面上存在正应力, 故可由扭转频率值推算剪切模量, 式(1)右边第2项Gcorrected计入是必需的。
式(1)表明: 对于悬臂板利用一阶扭转频率推算剪切模量时, 要用一阶弯曲频率推算出弹性模量E后, 将其代入式(1), 才能用一阶扭转频率推算出剪切模量G。
2 振形系数 C1、C2
振形系数与板材料和尺寸有关。下面分别给出各向同性材料(低碳钢)和正交各向异性材料(木材)振形系数依赖于悬臂板宽长比和厚宽比的关系式。2.1低碳钢振形系数
对于低碳钢l/b=1~7、b/h=4~50等24种不同长宽比和宽厚比的悬臂矩形杆件, 应用ANSYS软件solid45单元进行模态分析, 输入材料特性参数: 弹性模量E=200 GPa, 泊松比μ=0.28, 密度ρ=7.8 g·cm-3。从模态分析的一阶扭转振形得到C1、C2, 并应用二元回归分析得到C1、C2依赖于悬臂板宽长比和厚宽比的相关式。低碳钢的弹性模量、剪切模量和悬臂板一阶扭转频率的关系可表示为:
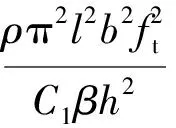
(2)
式中:C1=7.278 2+2.244 0b/l-1.332 9h/b(R=0.995 0,n=24);C2=-0.002 3+0.129 2b/l-0.113 0h/b(R=0.995 2,n=24)。
2.2木材振形系数
在进行ANSYS模态计算时, 对云杉(Piceaasperata)、山毛榉(Faguslongipetiolata)和欧洲赤松(Pinussylvestris)3个树种的弦切面、径切面和横切面(水平面)试件送入相应的主向弹性常数(王正等, 2014; 2016; 尹思慈, 1996)。
弦切面、径切面试件计算的悬臂板尺寸为l/b=5、4、3和2,b/h=5、6.83、10.08和13.67, 每个树种的试件尺寸有16种组合。横切面试件计算的悬臂板尺寸为l/b=4、3和2,b/h=5、6.83、10.08和13.67, 每个树种的试件尺寸有12种组合。
采用ANSYS软件solid45单元, 输入材料特性参数, 进行ANSYS模态分析。从模态分析结果中取出一阶扭转振形, 根据一阶扭转振形的z、x向位移分量w、u拟合得到云杉、山毛榉和欧洲赤松在不同宽长比和厚宽比下的悬臂板振形系数C1、C2。
为寻求适用于不同树种, 即适用于木材的C1、C2随b/l、h/b的变化规律, 首先将同一宽长比、同一厚宽比下的3个树种C1、C2取平均值作为木材在该宽长比、厚宽比下的C1、C2数值, 再对其作二元回归分析,得到木材振形系数C1、C2依赖于悬臂板宽长比、厚宽比的回归关系式。对于木材有:
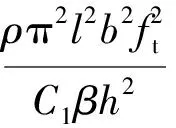
(3)
式中:弦切面C1=7.343 7+5.689 0b/l-2.185 9h/b(R=0.996 5,n=16);C2=0.004 82+0.040 78b/l-0.034 15h/b(R=0.988 5,n=16)。径切面C1=7.480 9+4.462 4b/l-2.998 0h/b(R=0.991 7,n=16);C2=0.007 63+0.040 32b/l-0.053 51h/b(R=0.963 8,n=16)。横切面C1=7.089 6+6.021 2b/l-0.512 1h/b(R=0.999 8,n=12);C2=-0.000 5+0.064 26b/l-0.007 31h/b(R=0.999 6,n=12)。
这里需说明的是,式(2)或式(3)的导出仅用了悬臂板一阶扭转模态中的振形模态参数, 尚未用一阶扭转频率这一模态参数, 因此式(2)或式(3)的正确性还有待于验证。以下从剪切模量仿真计算、剪切模量动态和静态测试3个方面加以验证,动态试验验证实质是测试悬臂板的一阶扭转频率和一阶弯曲频率。
先用测试的一阶弯曲频率fb按下式推算弹性模量E(提摩盛科, 1963):
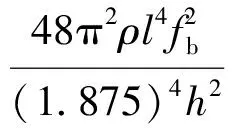
(4)
式中:fb为悬臂矩形杆件一阶弯曲频率。
然后将推算的E代入式(2)或式(3), 再用测试的一阶扭转频率ft推算出剪切模量G。
3 剪切模量仿真计算
3.1低碳钢和轧制铝
为验证式(2)的正确性,选用低碳钢和轧制铝对其进行剪切模量的仿真计算。ANSYS模态计算输入的材料特性参数如下: 低碳钢E=200 GPa,μ=0.28,ρ=7.8 g·cm-3;轧制铝E=68 GPa,μ=0.34,ρ=2.7 g·cm-3。先用计算的一阶弯曲频率fb按式(4)推算弹性模量E,然后将推算的E代入式(2), 再用测试的一阶扭转频率ft推算出剪切模量G, 剪切模量仿真计算过程及其结果如表1所示。
由表1可知:Gcorrected随悬臂板长宽比减小而快速增加,为得到正确的剪切模量仿真值Gcorrected是必需的; 式(2)中振形系数虽由低碳钢得到,但也适用于推算轧制铝的剪切模量。
3.2木材
选择桃花心木(Swieteniamahagoni)、白蜡木(Fraxinusamericana)和轻木(Ochromalagopus)3个树种进行弦切面剪切模量的仿真计算以验证式(3)的正确性。应用ANSYS程序输入各自与弦切面相关的9个材料常数和密度(王正等, 2016),计算出不同试件尺寸(试件宽度皆为123 mm)下的一阶弯曲频率fb和一阶扭转频率ft, 用fb按式(4)推算出各自的弹性模量E后, 再将ft代入式(3)推算出剪切模量。计算过程和结果如表2所示。
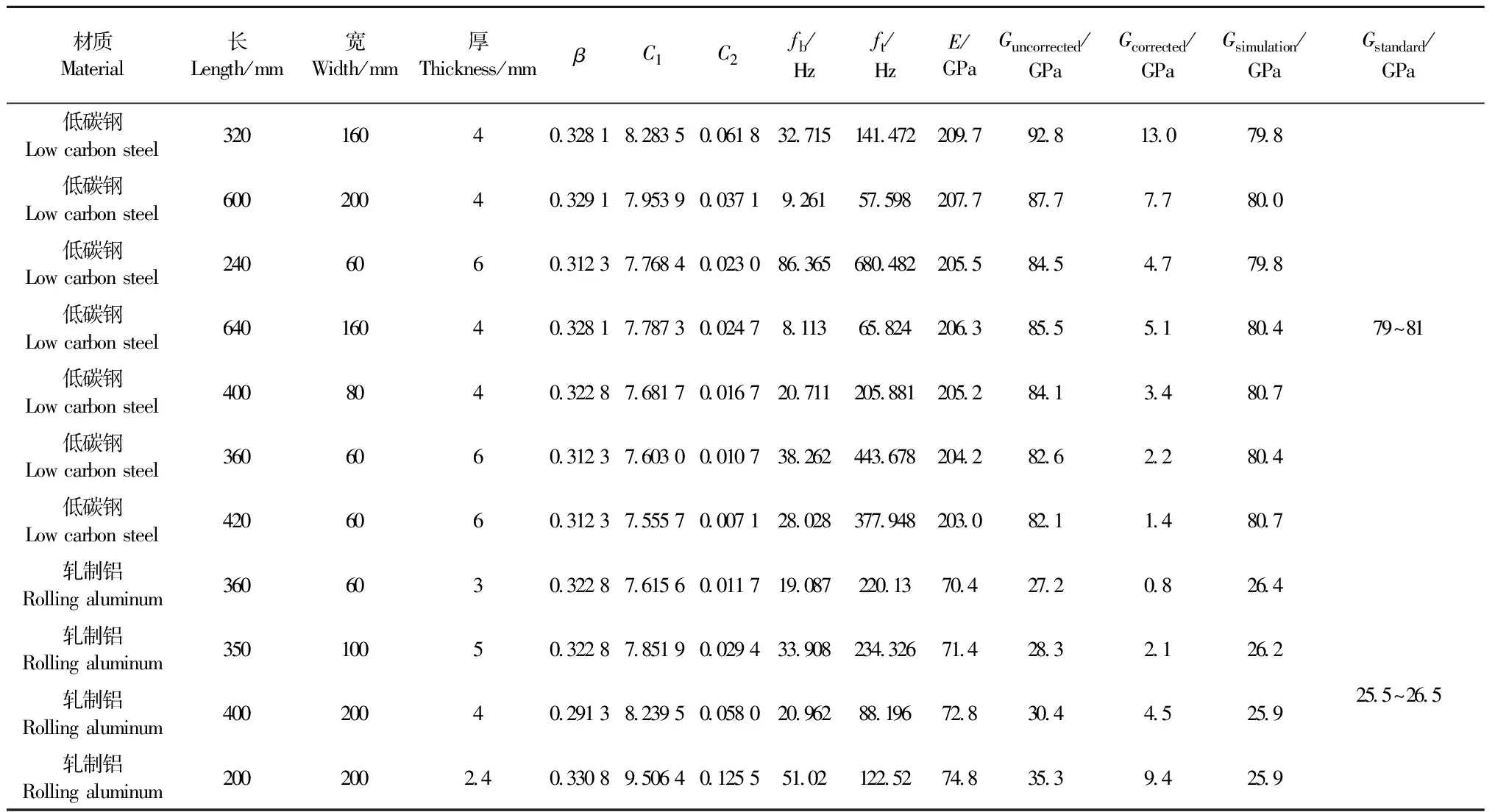
表1 低碳钢和轧制铝剪切模量仿真过程及其仿真值Tab.1 Shear modulus simulation process and values of low carbon steel and rolling aluminum

表2 桃花心木、白蜡木和轻木剪切模量仿真值及其规范值①Tab.2 Shear modulus simulation and standard values of Swietenia mahagoni, Fraxinus americana and Ochroma lagopus
①括号内的数据表示剪切模量仿真值与规范值的比值。The data in parentheses represent the radio of the shear modulus to the standard value.
由表2可知: 1) 对于3个树种, 长宽比2~6.83、宽厚比6.83~13.67的悬臂板, 仿真计算的剪切模量与其规范值相差均小于7%; 2) 随着杆件长宽比减少,Gcorrected项影响快速增加,说明G的修正项是必需的。这就从仿真角度验证了式(3)的正确性。从表2所列的弹性模量数据还发现,用计算的一阶弯曲频率代入到式(4)推算出的弹性模量与应用ANSYS模态程序送入的弹性模量数值几乎是相同的。
4 剪切模量试验
4.1动态试验框图
图2为测量悬臂矩形杆件频谱的试验框图。加速度计安装于悬臂板长边距固定端0.2~0.3l处。锤击试件角点,激励悬臂板自由振动, 通过加速度计接收振动信号并转换为电信号输出, 再经AZ-802型调理仪将电信号放大、滤波后输入到采集箱,经AD转换将模拟信号变为数字信号, 最后应用信号和系统分析软件SsCras处理并在计算机屏幕上显示试件频谱,从频谱上可读取试件的一阶弯曲频率和一阶扭转频率。
推荐用互功率法识别悬臂板试件频谱图上的一阶弯曲频率和一阶扭转频率。
4.2测量对象及其试件尺寸
低碳钢剪切模量的动态测试: 钢板试件公称尺寸360 mm×60 mm×3 mm, 实现悬臂夹持, 外伸长度300 mm(l/b=5)。
西加云杉(Piceasitchensis)顺纹-径切面剪切模量GLR动态测试: 实测西加云杉的气干密度为0.373 g·cm-3,对500 mm×123 mm×12.2 mm的矩形板, 其夹持深度为50 mm, 以实现450 mm×123 mm×12.2 mm的悬臂板试件。

图2 测量悬臂矩形杆件频谱的试验框图Fig.2 Test diagram for measuring spectrum of rectangular cantilever bar
西加云杉水平面剪切模量GRT的动态测试: 试件公称尺寸300 mm×60 mm×12.2 mm,其夹持深度60 mm,实现l/b=4的悬臂板试件。
蒙古栎(Quercusmongolica)剪切模量的动态测试: 自由板试件公称尺寸 910 mm×130 mm×18 mm,悬臂板试件公称尺寸717 mm×130 mm×18 mm,其悬臂外伸长度650 mm。自由板试件借助王正等(2014)方法测得剪切模量后,将自由板试件截短作悬臂板试件。蒙古栎试件来自地板毛坯料,既不是弦切也不是径切向下料,故称为蒙古栎顺纹剪切模量。
油松(Pinustabulaeformis)剪切模量GLT和GLR的动态测试: 试件公称尺寸360 mm×60 mm×12.2 mm,其夹持深度60 mm,实现300 mm×60 mm×12.2 mm的悬臂板试件。
4.3方板剪切模量静态扭转试验
采用方板静态扭转试验测试剪切模量,以验证基于悬臂板扭转模态测试剪切模量原理和方法的正确性。方板扭转试验受力和粘贴应变片位置如图3所示。

图3 方板扭转试验示意Fig.3 Diagram of square plate torsion test
试件树种与切面: 西加云杉径切面和横切面; 油松径切面和弦切面; 蒙古栎顺纹。
为验证动态测试剪切模量原理和方法的正确性,考虑同一树种因产地不同引起材料弹性常数差异,故采用从悬臂板试件截取方板试件,且方板试件与悬臂板试件取相同的试件编号。
测试仪器设备为上海华东YD-28A型动静态应变仪、BX120-5AA型应变片(阻值120 Ω、灵敏系数: 2.08%±1%、应变栅长度和宽度分别为5 mm和3 mm)和南京安正AZ308R型信号采集箱以及数据采集软件。
砝码加载:设定下限载荷和上限载荷, 若载荷差值记作ΔP, 相应的应变差值记作Δε, 则方板扭转试验测试的剪切模量计算式为:
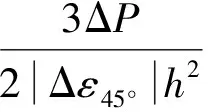
每一试件进行3次测试, 取后2次剪切模量测试值的平均值作为该试件的剪切模量测试值。
5 结果与分析
5.1低碳钢剪切模量的动态测试
悬臂钢板1号试件频谱如图4所示。悬臂钢板一阶弯曲频率推算弹性模量见式(4)、一阶扭转频率推算钢材剪切模量见式(2),钢材弹性模量和剪切模量测量值如表3所示。

图4 悬臂钢板1号试件频谱Fig.4 Frequency spectrum of the first specimen of the cantilever steel plate

表3 钢材弹性模量和剪切模量测量值Tab.3 Measured values of elastic modulus and shear modulus of steel
由表3可知,钢材试件的弹性模量测量均值为191.2 GPa,变异系数为2.8%; 剪切模量测量均值为79.4 GPa,变异系数为3.0%。
5.2西加云杉剪切模量的动态测试
5.2.1 西加云杉顺纹-径切面剪切模量GLR动态测试 西加云杉径切面X4悬臂板试件频谱如图5所示,从频谱图的第一高峰与第二高峰可读取一阶弯曲频率为49.06 Hz、一阶扭转频率为165.94 Hz。一阶扭转频率测试值推算剪切模量的公式见式(3),测试西加云杉顺纹-径切面剪切模量结果见表4。
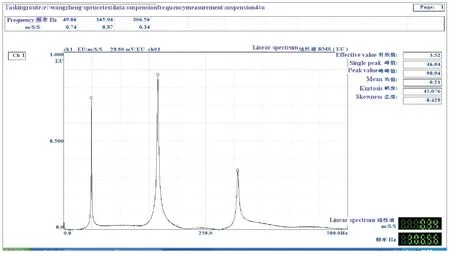
图5 西加云杉径切面X4悬臂试件频谱Fig.5 Spectrum of the cantilever specimen X4 made by Picea sitchensis(radial section)

表4 西加云杉顺纹-径切面剪切模量GLR动态测试值(实测密度373 kg·m-3)Tab.4 Dynamic test value GLR which is the shear modulus of radial section parallel to grain of Picea sitchensis (measured density=373 kg·m-3)
表4中最后一列括号内数值为自由支承状态用500 mm×123 mm×12.2 mm试件按王正等(2014)方法测得的剪切模量: 平均值=0.682 GPa,标准离差=0.023 GPa,变异系数=3.3%。而表4中悬臂支承状态测试剪切模量:平均值=0.673 GPa,标准离差=0.033 GPa,变异系数=4.9%。
5.2.2 西加云杉水平面剪切模量GRT的动态测试西加云杉水平面(横面)XH1悬臂试件频谱如图6所示。从图6频谱图的第一高峰与第二高峰可读取一阶弯曲频率为51.88 Hz、一阶扭转频率为150.63 Hz。
测试西加云杉水平面剪切模量结果见表5。

图6 西加云杉水平面(横面)XH1悬臂试件频谱Fig.6 Spectrum of the cantilever specimen XH1 made by Picea sitchensis(cross section)
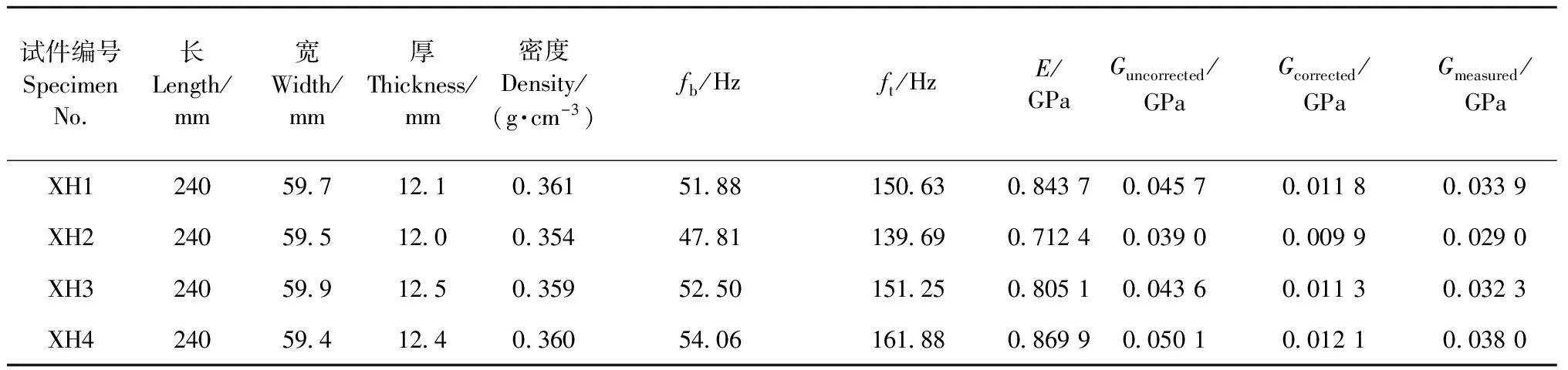
表5 西加云杉水平面剪切模量GRT动态测试值Tab.5 Dynamic test value GRT which is the shear modulus in cross section of Picea sitchensis
表5中,悬臂支承状态测试西加云杉水平面剪切模量GRT:平均值=0.033 6 GPa,变异系数=11.2%; 而自由状态测试西加云杉水平面剪切模量GRT:平均值=0.034 3 GPa,变异系数=12.3%(王正等, 2014)。
5.3蒙古栎剪切模量的动态测试
蒙古栎2号试件在悬臂板支承测得的频谱如图7所示。表6显示了在悬臂支承下测得的蒙古栎剪切模量。

图7 蒙木栎2号悬臂试件频谱Fig.7 Spectrum of the secondcantilever specimen made by Quercus mongolica
表6中,用悬臂板支承状态测得蒙古栎剪切模量均值为1.40 GPa, 变异系数为14.6%; 按王正等(2014)借助自由板测得蒙古栎剪切模量均值为1.39 GPa, 变异系数为14.3%(见表6最后一列括号内数据)。
5.4油松剪切模量GLT和GLR的动态测试
由表7得知,油松径切面剪切模量GLR在悬臂支承状态下测试的均值为1.074 GPa,变异系数为9.7%。而在自由支承状态下(见表7最后一列括号内数据,下同)测试油松径切面GLR剪切模量的均值为1.041 GPa, 变异系数为10.6%(王正等, 2016); 油松弦切面剪切模量GLT在悬臂支承状态下测试的均值为0.757 GPa, 变异系数为10.7%; 弦切面剪切模量GLT均值为0.777 GPa,变异系数为15.2%(王正等, 2016)。
5.5方板剪切模量静态扭转试验
结果见表8。
5.6动态测试和静态方板扭转测试的剪切模量比较
动态测试剪切模量包括基于悬臂板扭转模态法和自由板扭转振形法测试的剪切模量,其与方板静态扭转法测试的剪切模量如表9所示。

表6 蒙古栎动态剪切模量测试值Tab.6 Test value of dynamic shear modulus of Quercus mongolica

图8 油松(径切面)悬臂试件Y4频谱Fig.8 Spectrum of the cantilever specimen Y4 by Pinus tabulaeformis(radial section)

表7 国产油松径切面GLR和弦切面GLT剪切模量动态测试值Tab.7 Dynamic test value of the shear modulus in radial sections GLR and shear modulus in tangential sections GLT of Pinus tabulaeformis

表8 蒙古栎、油松弦切面和径切面以及西加云杉径切面和横切面方板扭转试验测试的静剪切模量Tab.8 The square plate torsion testing static shear modulus of the radial section and the tangential section by Quercus mongolica, Pinus tabulaeformis and the radial section and the cross section by Picea sitchensis
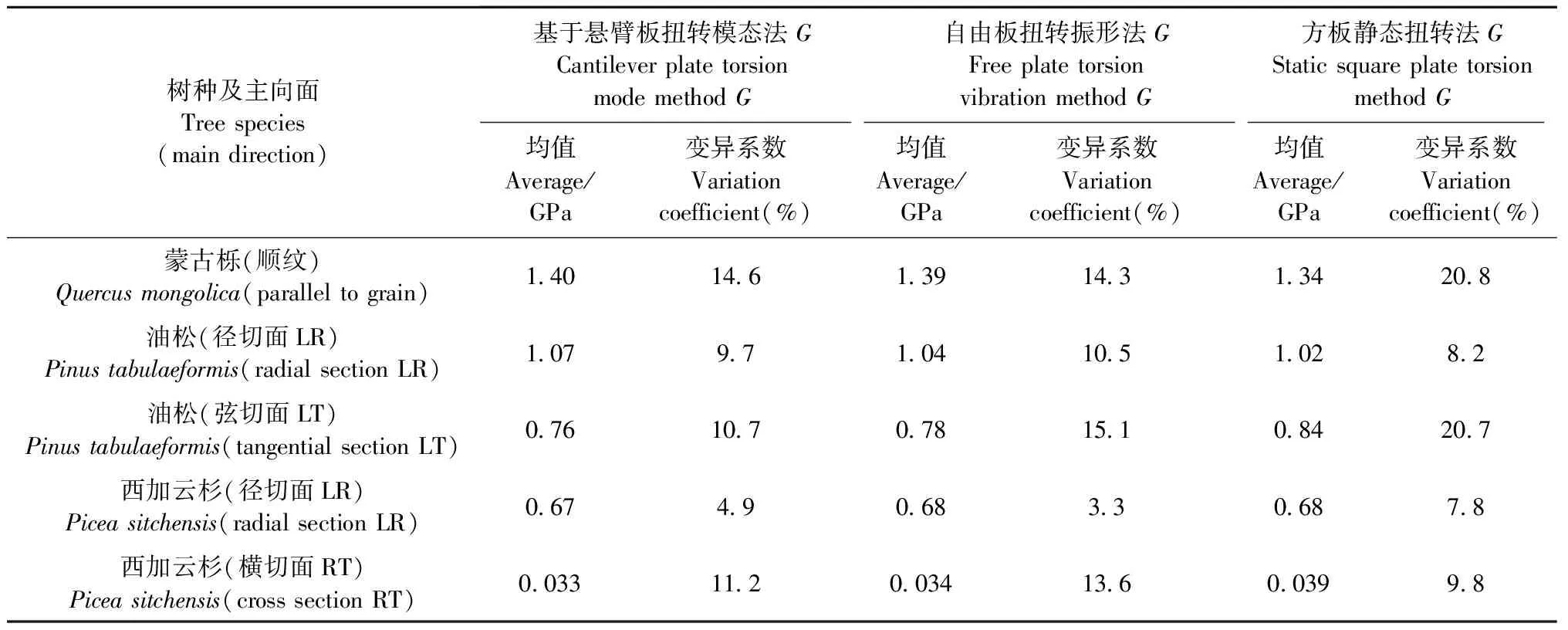
表9 蒙古栎、油松和西加云杉剪切模量动态、静态测试值对比Tab.9 The comparison of shear modulus by static and dynamic methods of Quercus mongolica, Pinus tabulaeformis and Picea sitchensis
由表9可知: 自由板扭转振形法和基于悬臂板扭转模态法测出的剪切模量相当吻合,说明测量参数与约束状况无关,体现了测量参数是材料特性, 也说明了悬臂板的振形系数C1、C2用于测试剪切模量是正确的。基于悬臂板扭转模态法、自由板扭转振形法和方板静态扭转法测得的剪切模量从均值意义来说相当一致, 但就数据分散性而言, 动态测试的分散性小于静态,其原因为自由板和悬臂板皆是测试一阶扭转频率获得剪切模量测量值, 而频率反映的是试件整体刚性, 对于静态方板扭转法是通过测量应变推算剪切模量, 应变是局部特性, 而且木材又是正交各向异性, 分散性大些就不难理解。从此意义上说, 动态测试G比静态要优越些。
对于金属材料, 例如悬臂钢板用本文方法测得的弹性模量和剪切模量均与规范值一致, 说明基于悬臂板扭转模态的方法适用于测量金属(各向同性材料)剪切模量。
对于木材,动态测试的主向剪切模量和方板扭转试验测得的主向剪切模量一致,说明基于悬臂板扭转模态法适用于测试木材3个主向剪切模量。
5.7悬臂板一阶扭转频率、弹性模量和剪切模量耦合关系式分析
悬臂板一阶扭转频率推算剪切模量由2部分组成:
G=Guncorrected-Gcorrected。
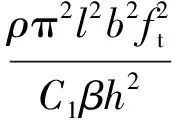
从仿真计算结果(表1、表2)看到, 计入Gcorrected项后,G的仿真值才能与其规范值一致; 从动态测试和静态测试结果(表9)看到,计入Gcorrected项后,G的动态测试值才能与静态测试值或自由板动态测试值一致,这充分说明用悬臂板测试剪切模量,不能只用Guncorrected项加以计算,必须计入Gcorrected项。
从西加云杉、蒙古栎和油松等树种动态测试的剪切模量(表4~7)考查Gcorrected/Guncorrected(用百分数%表示), 其结果见表10, 从表10看到Gcorrected/Guncorrected与树种、试件主向面和试件长宽比有关, 随着试件长宽比增加,Gcorrected/Guncorrected下降。
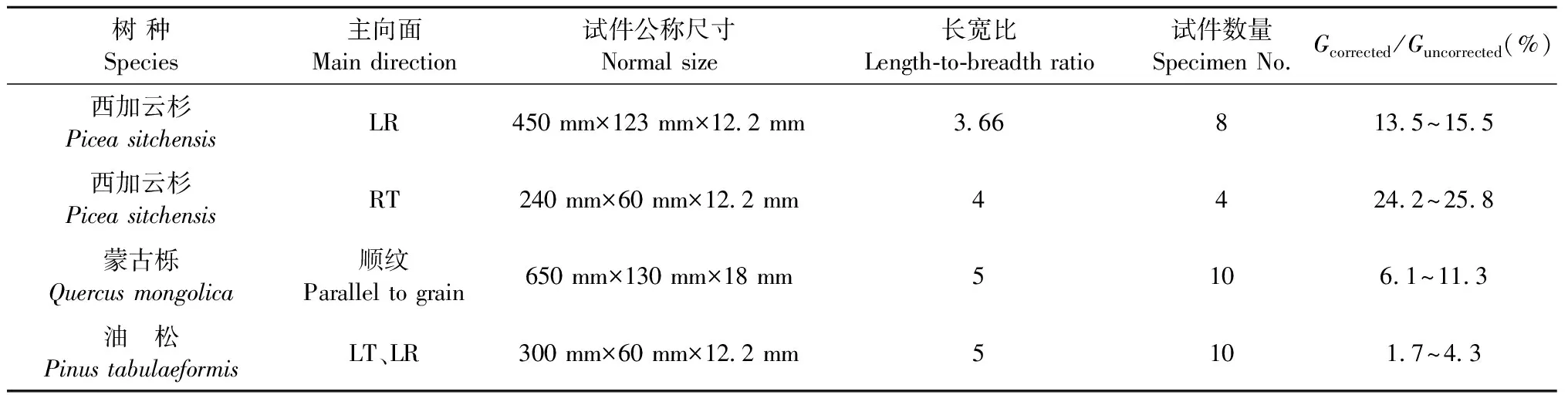
表10 西加云杉、蒙古栎与油松剪切模量G中Gcorrected项占Guncorrected项的百分数Tab.10 Gcorrected/Guncorrected of Picea sitchensis, Quercus mongolica and Pinus tabulaeformis
对于木质刨花板和胶合板,可视为准各向同性材料, 可近似用各向同性材料式(2)计算不同长宽比和宽厚比下的C1和C2, 宽厚比等于30(b/h=30)的不同长宽比悬臂板的C1和C2值如表11所示。
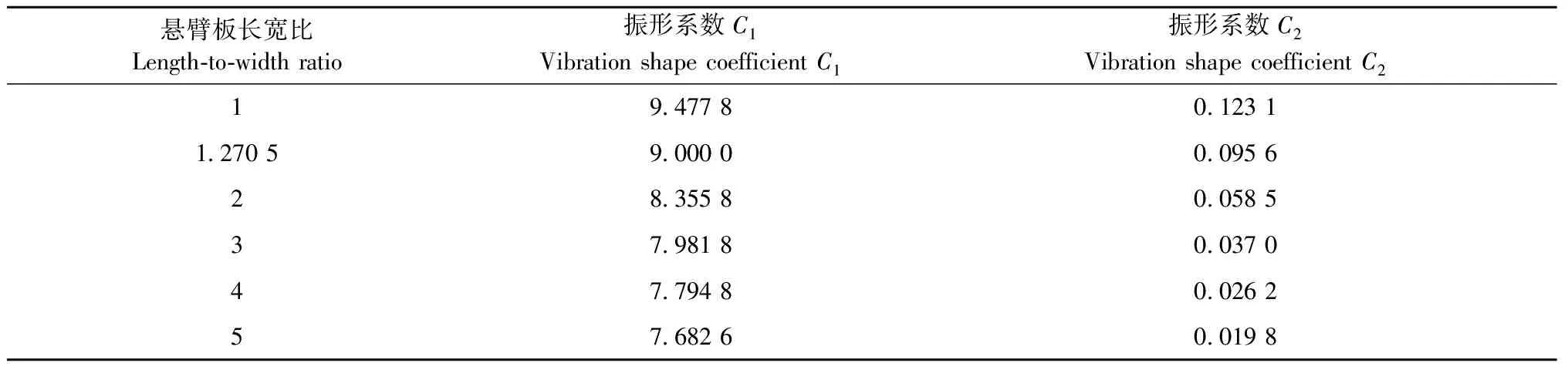
表11 宽厚比b/h=30的各向同性悬臂板振形系数Tab.11 Vibration shape coefficients of isotropic cantilever plates(b/h=30)
6 结论
1) 弹性模量、剪切模量和悬臂板一阶扭转频率之间满足耦合关系式,其中的振形系数C1和C2可用悬臂板宽长比和厚宽比的相关式计算。
2) 悬臂板一阶扭转模态导出的弹性模量、剪切模量和悬臂板一阶扭转频率之间耦合关系式的正确性得到金属材料和木材剪切模量仿真计算的验证。
3) 对于各向同性材料的金属材料和各向异性材料的木材,以悬臂板为试件用动态法测试的剪切模量与用静态方板扭转法测试的剪切模量吻合得较好,静态方板扭转试验验证了基于悬臂板扭转模态测试材料剪切模量的方法是正确的。
4) 悬臂板扭转模态法与自由板扭转振形法动态测试木材或各向同性材料的剪切模量相当吻合。
5) 悬臂板扭转模态法提供了一种用悬臂板频谱测试材料剪切模量的简便、快速方法,该方法不但适用于测试木材3个主向剪切模量GLT、GLR和GRT,还适用于测试各向同性材料的剪切模量。
程 可,王 正. 2015. 基于自由板扭转振形测试剪切模量的一个新方法. 南京工业大学学报: 自然科学版,37(5):61-66
(Cheng K,Wang Z. 2015. New method for testing shear modulus based on torsional vibration shape of free plate. Journal of Nanjing Tech University: Natural Science Edition,37(5):61-66.[in Chinese])
提摩盛科. 1965. 机械振动学. 北京: 机械工业出版社,316-333.
(Cheng Ke Timothy. 1965. Mechanical vibrational science. Beijing: Mechanical Industry Press,316-333.[in Chinese])
胡英成,王逢瑚,刘一星,等. 2001a. 利用振动法检测胶合板的剪切弹性模量. 木材工业,15(4):12-14.
(Hu Y C,Wang F H, Liu Y X,etal. 2001a. Study on modulus of elasticity in bending of plywood by vibration method. China Wood Industry,15(4):12-14. [in Chinese])
胡英成,王逢瑚,刘一星,等. 2001b. 刨花板的动态剪切弹性模量的无损检测. 东北林业大学学报,29(2):17-20.
(Hu Y C,Wang F H, Liu Y X,etal. 2001b. Nondestructive testing of the dynamic shear modulus of elasticity for panticleboard. Journal of Northeast Forestry University,29(2):17-20. [in Chinese])
刘镇波,刘一星,于海鹏,等. 2005.实木板材的动态弹性模量检测. 林业科学,41(6):126-131.
(Liu Z B,Liu Y X,Yu H P,etal. 2005. Research on the dynamic modulus of elasticity measurement of lumber. Scientia silvae sinicae, 41(6):126-131. [in Chinese])
王 正. 2007. 两种木质复合材料弹性模量与阻尼比的动态测量. 南京林业大学学报,31(3):147-149.
(Wang Z. 2007. Dynamic measure of elasticity model and damp ratio to HDF and OSB. Journal of Nanjing Forestry University,31(3):147-149.[in Chinese])
王 正,饶 鑫,杨小军,等. 2013. 轻型木结构规格材抗弯弹模的两种无损法检测与评级. 林产工业,40(5):30-33.
(Wang Z,Rao X,Yang X J,etal. 2013. Non-destructive testing and ratings of MOE of SPF stock lumbers by the frequency method and sound velocity method. China Forest Products Industry,40(5):30-33. [in Chinese])
王 正,顾玲玲,高子震,等. 2015. SPF规格材弹性模量的动态测试及其概率分布. 林业科学,51(2):105-111.
(Wang Z,Gu L L,Gao Z Z,etal. 2015. Dynamic testing and probability distribution of elastic modulus of SPF dimension lumbers. Scientia Silvae Sinicae, 51(2):105-111. [in Chinese])
王 正,高子震,顾玲玲,等. 2014. 测试木材剪切模量的自由板扭转振形法. 林业科学,50(11):122-128.
(Wang Z,Gao Z Z,Gu L L,etal. 2014.Torsional vibration shape method of free plate for testing shear modulus of lumber. Scientia Silvae Sinicae, 50 (11): 122-128. [in Chinese])
王 正,王韵璐,曹 瑜,等. 2016. 自由板扭转振形法测定木材剪切模量、GLT、GLR和GRT. 林业工程学报,1(3): 10-17.
(Wang Z,Wang Y L,Cao Y,etal. 2016. Torsional vibration method for free board determining the shear modulus of woodGLT,GLRandGRT. Journal of Forestry Engineering,1(3): 10-17.[in Chinese])
王志同. 1991. 无损测试技术在木材工业中的应用. 世界林业研究,(4):64-68.
(Wang Z T. 1991. Application of the non-destructive testing technique to wood industry. World Forestry Research,(4):64-68. [in Chinese])
王志同,曹志国,袁卫国. 1995. 用应力波非破损检测技术检测中密度纤维板弹性模量的研究. 木材工业,9(5):21-25.
(Wang Z T,Cao Z G,Yuan W G.1995.The testing research on the elastic modulus of medium density fiberboard by the nondestructive examination (NDE)technique of stress wave.China Wood Industry, 9(5):21-25. [in Chinese])
尹思慈. 1996. 木材学. 北京: 中国林业出版社.
(Yin S C. 1996. Wood science. Beiing: China Forestry Publishing House. [in Chinese])
张厚江,申世杰,崔英颖,等. 2005.振动方式测试木材弹性模量. 北京林业大学学报,27(6):91-94.
(Zhang H J,Shen S J,Cui Y Y,etal. 2005. Measuring elastic modulus of wood vibration method. Journal of Beijing Forestry University, 27(6):91-94.[in Chinese])
周海宾,任海青,殷亚方,等. 2007a. 横向振动评估木结构建筑用规格材弹性性质. 建筑材料学报,10(3):272-275.
(Zhou H B,Ren H Q,Yin Y F,etal. 2007a. Evaluating static elastic properties of wood structure building dimension lumber using transverse vibration. Journal of Building Materials,10(3):272-275. [in Chinese])
周海宾,任海青,费本华,等. 2007b. 木质复合板弯曲、剪切弹性模量动态测试. 建筑材料学报,10(5):561-565.
(Zhou H B,Ren H Q,Fei B H,etal. 2007b. Dynamical test on flexural and shear modulus of composite wood panels. Journal of Building Materials,10(5):561-565. [in Chinese])
Gulzow A,Klaus R,René S. 2011. Influence of wood moisture content on bending and shear stiffness of cross laminated timber panels. Wood Prod, 69(2):193-197.
(责任编辑 石红青)
TestingShearModulusofMaterialsBasedonTorsionalModeofCantileverPlate
Wang Zheng Cao Yu Wang Yunlu Li Minmin
(CollegeofMaterialsScienceandEngineering,NanjingForestryUniversityNanjing210037)
TS643
A
1001-7488(2017)08-0101-12
10.11707/j.1001-7488.20170812
2016-03-21;
2016-06-20。
江苏省高校优势学科建设工程项目资助(PAPD); 2017年江苏省林业科技创新与推广项目(LYKJ[2017]41); 2015年江苏省大学生创新训练计划项目(201510298111X)。

