变量加权型主元分析算法及其在故障检测中的应用

蓝艇，童楚东，史旭华



变量加权型主元分析算法及其在故障检测中的应用

蓝艇，童楚东，史旭华

（宁波大学信息科学与工程学院，浙江宁波 315211）

传统主成分分析（PCA）算法旨在挖掘训练数据各变量间的相关性特征，已在数据驱动的故障检测领域得到了广泛的研究与应用。然而，传统PCA方法在建模过程中通常认为各个测量变量的重要性是一致的，因此不能有效而全面地描述出变量间相关性的差异。为此，提出一种变量加权型PCA（VWPCA）算法并将之应用于故障检测。首先，通过对训练数据进行加权处理，使处理后的数据能够充分体现出变量间相关性的差异。然后，在此基础上建立分布式的PCA故障检测模型。在线实施故障检测时，则通过贝叶斯准则将多组监测结果融合为一组概率指标。VWPCA方法通过相关性大小为各变量赋予不同的权值，从而将相关性差异考虑进了PCA的建模过程中，相应模型对训练数据特征的描述也就更全面。最后，通过在TE过程上的测试验证VWPCA方法用于故障检测的优越性。

主元分析；过程系统；过程控制；故障检测

引 言

在整个综合自动化系统中，故障检测系统可谓是必不可少的组成部分，因为实时监测生产过程的运行状态是保证生产安全和维持产品质量稳定的必要手段。近年来，得益于各种先进仪表与计算技术的广泛应用，工业过程可以测量和存储海量的数据样本。实施故障检测不再依赖于基于机理模型的过程监测方法，取而代之的是以生产过程采样数据为核心的数据驱动的过程监测方法[1-4]。作为数据驱动的过程监测方法的一个重要研究分支，多变量统计过程监测（multivariate statistical process monitoring, MSMP）方法于近年来受到了工业界和学术界的广泛关注，其核心思想在于利用过程正常数据建立能描述过程正常运行状态的统计模型，从而实现对过程是否发生故障进行监测的目的[5-8]。

在现有的多变量统计过程监测方法体系中，主元分析（principal component analysis, PCA）是最常用的数据分析算法，已被广泛用于工业过程监测实践中，各种延伸拓展形式层出不穷[9-12]。通常来讲，PCA算法旨在挖掘原始高维数据变量间的相关性特征，使提取的低维特征子空间最大化保留方差信息。在建模过程中，为了消除各变量变化幅值对方差的影响，基于PCA的过程监测方法需将采样数据按变量进行标准化处理，即所有的测量变量都被归一化。从某种角度上看，所有测量变量其实都是被赋予了相同的权值，各个测量变量在投影变换过程中的重要性是一致的。这种数据预处理方式对PCA这类旨在挖掘数据变量相关性的分析算法而言，有一个缺陷：数据变量间的相关性是存在差异的，若不对数据变量间的相关性差异进行有效地权衡，PCA模型所提取的潜藏信息无法全面而有效地描述过程运行的状态。针对这一问题，Ge等[13-16]从数据统计特性角度出发对变量进行分块处理，进而提出基于分布式PCA（distributed PCA, DPCA）的过程监测方法。DPCA方法能在一定程度上区分变量间的相关性，而且还利用了多模型的泛化能力，因此能取得优越于传统PCA方法的故障检测效果。

然而，分布式PCA方法在建模过程中有两个问题还未得到深入研究探讨。首先，变量分块需要一个截断阀值将相关性较大的变量区分出来，截断阀值的选取无章可循，而且对模型监测结果影响较大。其次，每个测量变量与其他变量间的相关性大小存在差异，这种差异未能得到充分的体现。因此，基于PCA尤其是基于分散式PCA的过程监测方法所能取得故障检测效果还有待进一步的商榷。为此，本文提出一种变量加权PCA（variable weighted PCA, VWPCA）算法并将之应用于工业故障检测。具体来讲，VWPCA首先依据每个测量变量与其他变量间的相关性大小对训练数据中各变量进行加权处理，然后对加权处理后的数据建立相应的PCA模型。也就是说，若过程对象有个测量变量，VWPCA会存在种不同的方式对训练数据进行变量加权处理，并相应建立种不同的PCA模型。最后，对在线新测量数据实施故障检测，调用每个PCA模型前需对其进行同样的变量加权处理。VWPCA方法通过相关性大小为各变量赋予不同的权值，将相关性差异考虑进了PCA的投影变换过程中，相应的PCA模型就能更全面地挖掘出原始数据中的相关性特征。可以说，基于VWPCA的过程监测方法综合考虑了分布式建模的优势与采样数据各变量相关性的差异。相比于传统的PCA或分布式PCA方法，它理应取得更好的故障检测效果。这一点，可在Tennessee Eastmann（TE）[9,17-18]仿真实验平台上的通过对比分析得到验证。

1 基于PCA的故障检测模型

1.1 传统PCA方法

假设经过标准化处理后的正常过程训练数据为∈R×m（为样本数，为变量数），对的协方差矩阵

进行特征值分解即可得到PCA统计模型，即[1]

=T+(2)

=(3)

=(-T) (4)

式中，∈R×d和∈R×d分别是得分矩阵和载荷矩阵，∈R×m为残差矩阵，<为选取的主元个数。载荷矩阵中各载荷向量[1,2,…,]即是协方差矩阵前个最大特征值1,1,…,所对应的特征向量。因此，PCA算法旨在挖掘训练数据中各变量间的相关性。

传统PCA模型主要依赖如下两个统计量监测新样本是否出现故障，即

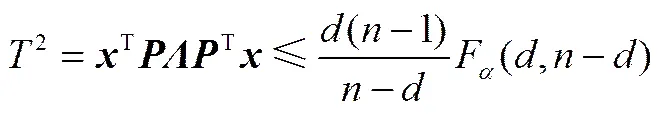
(6)

其中，=diag{1,2,…,}，为置信限，(,-)表示自由度为与-的分布，2,表示权重为=/2、自由度为=22/的加权2分布，与分别是统计量的估计均值和估计方差[19]。

1.2 分布式PCA方法

相比于传统PCA方法采用单个PCA模型监测过程运行状态而言，分布式PCA监测模型因采用多个PCA子模型而能显著提升故障检测效果。近年来，从数据统计特性角度出发设计DPCA故障检测模型得到了研究者们的青睐。其基本特点就是依据相关性强弱将测量变量划分为重叠或不重叠的变量子块，然后建立相应的子PCA故障检测模型。例如，Ge等[13,20]曾利用PCA模型的载荷向量区分变量间的相关性。依据各变量在载荷向量上的贡献程度来得到每个变量子块，即

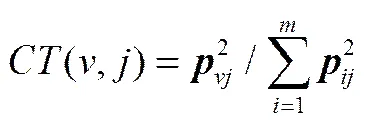
(8)

其中，=1,2,…,表示第变量，=1,2,…,表示第个子块，∈R×1是{+1,+2,…,}的均值向量。在线实施故障检测时，则利用贝叶斯准则将+1个PCA模型的监测结果融合为一个概率型指标（即：BIC2与BIC）[8,13]。

2 基于VWPCA的故障检测方法

2.1 变量加权PCA算法

过程变量间的相关性是存在差异的，对中某个变量（如∈R×1）而言，它与其他各变量的相关性大小差异如图1所示。考虑到PCA算法旨在挖掘变量间相关性特征，为了更好地体现出每个测量变量的相关性特征，需要对变量进行加权处理，具体的实施步骤介绍如下。

（1）针对第(=1,2,…,)个测量变量，计算其与中各个变量（=1,2,…,）间的相关性大小，即

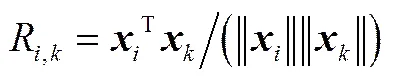
（2）根据相关性数值大小确定对应于第个变量的权向量=[|R,1|,|R,2|,…,|R,m|]，并对原始数据矩阵进行加权处理得到加权后的矩阵，即

=×diag() (10)

（3）利用训练数据建立基于PCA算法的故障检测模型，即

=PT+(11)

（4）重复步骤（1）～步骤（3）直至得到个PCA故障检测模型。

2.2 在线故障检测流程

利用VWPCA模型实施在线故障检测的流程如图2所示。首先，需利用节2.1节中的加权向量1,2,…,将新时刻的采样数据并行进行加权处理（即：=×diag()），对应得到1,2,…,。然后，利用相应PCA模型计算监测统计量2和Q

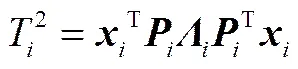
(13)

最后，采用贝叶斯准则[21]将组统计量融合为一组概率型指标。以统计量2为例，样本的故障概率为

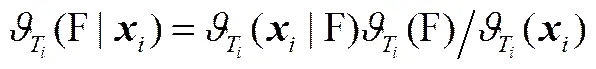
式中，=1,2,…,，概率定义如下

(15)

其中，C为统计量对应的控制限，其计算方式如式（5）所示。实际上，其他文献中也常采用式（16）中计算条件概率的方式[22-24]。最后，可按加权形式融合得到最终的概率监测指标BIC2

(17)

对统计量Q同样进行贝叶斯融合，同理可得到相应的BIC概率型指标。当BIC2>1-或BIC>1-时，为非正常样本，反之，过程处于正常工作状态。

3 仿真实验研究

TE仿真模型因其结构的复杂性，已成为不同控制方法和过程监测策略的标准实验平台[25-26]。TE过程主要有连续搅拌反应器、产品冷凝器、气液分离塔、汽提塔和离心式压缩机5个生产单元组成，可连续测量22个过程变量和12个操作变量，还可以仿真模拟如表1所列的21种不同的故障，详细资料可参考文献[17]。在本文的研究中，选取过程可连续测量的33个变量作为监测变量，详情可参考文献[13]。离线建模阶段，利用正常工况下的960个样本建立PCA、DPCA和VWPCA的过程监测模型以作对比分析用，置信限统一取值99%。其中，PCA模型涉及保留的主成分个数统一通过累计方差贡献率（CPV≥85%）准则确定。

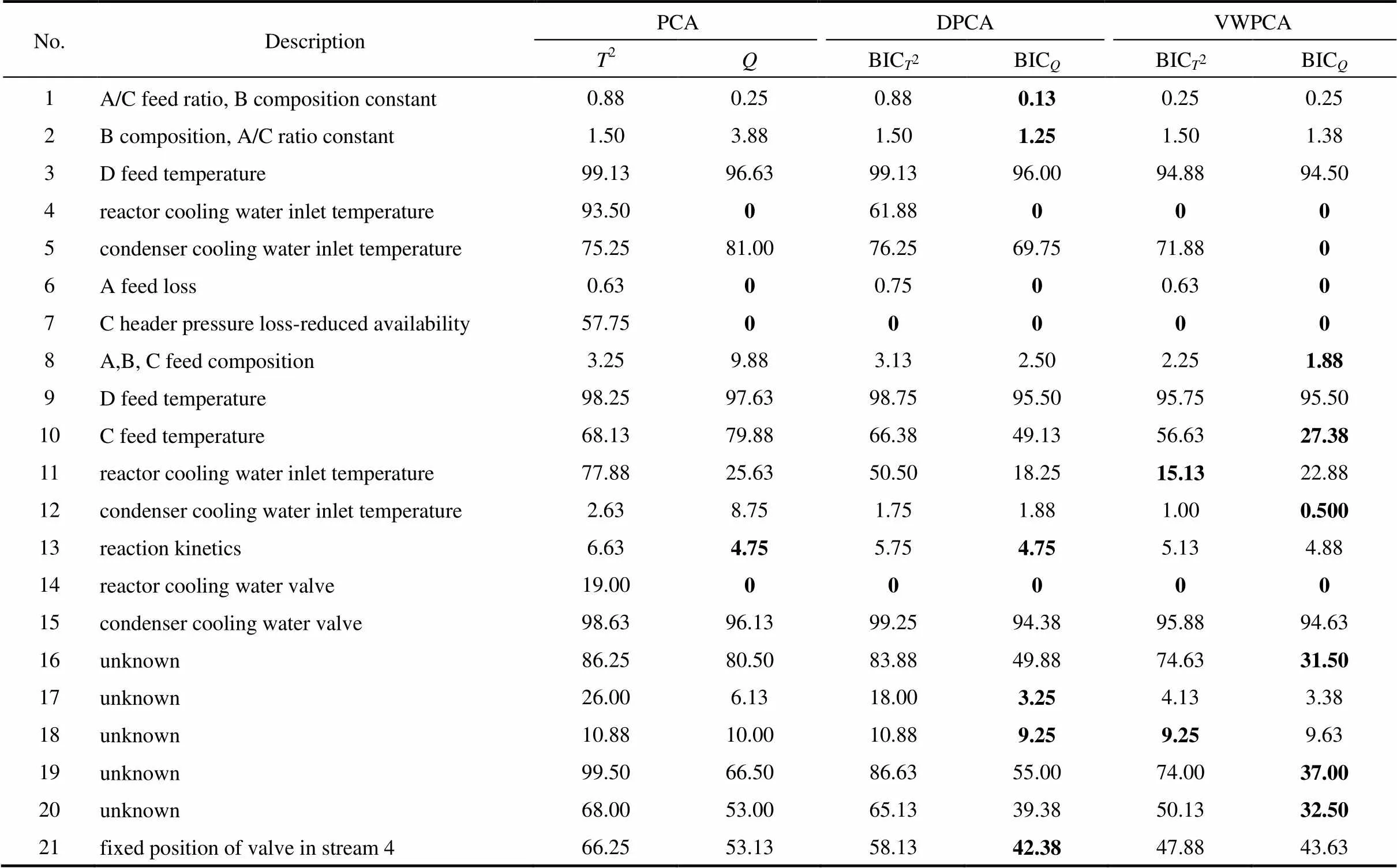
表1 TE过程故障漏报率

首先，将3种故障检测模型用于监测TE过程21种故障工况，并计算针对每种故障监测的故障漏报率，详情列于表1中。值得注意的是，故障3、9和15由于对过程的影响甚微，很多文献都证实这3种故障是很难被有效地检测出来的[27-29]。因此，在本研究中不予考虑。在表1中，取得最小漏报率的监测指标已用黑体标出。显而易见，本文所提出的VWPCA方法在绝大多数故障类型上能取得优越于传统PCA以及DPCA方法的故障检测结果。尤其是针对故障5、10、16、和19，故障漏报率得到大幅度的下降。为了更好地体现VWPCA相对于PCA与DPCA方法的优越性，特将故障5的过程监测图显示于图3中，可以较直观地看出3种方法在监测故障5时的漏报情况。此外，虽然VWPCA方法未在故障1、2、13、17和21上取得最佳监测效果，但相应的漏报率值相差微乎其微。

其次，为进一步说明VWPCA方法的可靠性，还需对比3种方法的故障误报率，即将正常数据样本错误的判别为故障。通常来讲，较低的故障漏报率会对应着较高的故障误报率。因此，利用另外一组500个正常样本组成的测试数据集测试PCA、DPCA以及VWPCA方法对正常工况的误报率。从表2中所列的故障误报率可以看出，VWPCA方法的两个统计量都能取得最低的故障误报率。相比于其他两种方法而言，本文所提出的VWPCA方法更可靠。通过上述对比分析，充分验证了基于VWPCA的过程监测方法的优越性和有效性。

表2 TE过程故障误报率

4 结 论

本文提出了一种基于分布式变量加权PCA模型的统计过程监测方法，旨在解决传统PCA方法或分布式PCA方法在建模过程中未曾体现出变量间相关性差异的问题。由于PCA算法旨在挖掘变量间的相关性特征，可通过对变量赋予不同的权值而将相关性差异充分体现出来。而在传统PCA建模方法中，各变量可认为被赋予了相同的权值，未能全面地描述变量间的相关性差异。相比之下，VWPCA方法能针对每个测量变量区分出其与其他变量间相关性差异，并建立最能描述该变量相关性特征的PCA模型。此外，该方法还利用了分布式建模方式，充分发挥了多模型的泛华能力，可取得更加可靠而有效的故障检测效果。然而，VWPCA仍旧是一种线性方法，传统PCA监测模型的缺陷同样存在于VWPCA中。如何应对非线性、非高斯、多工况的复杂过程对象对下一步的工作提出了挑战。此外，本文的研究只限于故障检测，还未涉及后续的故障诊断，未来需开展相应的研究工作。

References

[1] GE Z, SONG Z, GAO F. Review of recent research on data-based process monitoring[J]. Ind. Eng. Chem. Res., 2013, 52(10): 3543-3562.

[2] YIN S, DING S X, XIE X,. A review on basic data-driven approaches for industrial process monitoring[J]. IEEE Trans. Ind. Electron., 2014, 61(11): 6418-6428.

[3] 周乐, 宋执环, 侯北平, 等. 一种鲁棒半监督建模方法及其在化工过程故障检测中的应用[J]. 化工学报, 2017, 68(3): 1109-1115. ZHOU L, SONG Z H, HOU B P,. Robust semi-supervised modelling method and its application to fault detection in chemical processes[J]. CIESC Journal, 2017, 68(3): 1109-1115.

[4] 王磊, 邓晓刚, 徐莹, 等. 基于变量子域PCA的故障检测方法[J]. 化工学报, 2016, 67(10): 4300-4308. WANG L, DENG X G, XU Y,. Fault detection method based on variable sub-region PCA[J]. CIESC Journal, 2016, 67(10): 4300-4308.

[5] 童楚东, 史旭华. 基于互信息的PCA方法及其在过程监测中的应用[J]. 化工学报, 2015, 66(10): 4101-4106. TONG C D, SHI X H. Mutual information based PCA algorithm with application in process monitoring[J]. CIESC Journal, 2015, 66(10): 4101-4106.

[6] 江伟, 王振雷, 王昕. 基于混合分块DMICA-PCA的全流程过程监控方法[J]. 化工学报, 2017, 68(2): 759-766. JIANG W, WANG Z L, WANG X. Plant-wide process monitoring based on mixed multiblock DMICA-PCA[J]. CIESC Journal, 2017, 68(2): 759-766.

[7] TONG C, LAN T, SHI X. Double-layer ensemble monitoring of non-Gaussian processes using modified independent component analysis[J]. ISA Trans., 2017, 68: 181-188.

[8] 胡永兵, 高学金, 李亚芬, 等. 基于仿射传播聚类子集主元分析的间歇过程监测方法[J]. 化工学报, 2016,67(5): 1989-1997. HU Y B, GAO X J, LI Y F,. Subset multiway principal component analysis monitoring for batch process based on affinity propagation clustering[J]. CIESC Journal, 2016,67(5): 1989-1997.

[9] RATO T J, REIS M S. Fault detection in the Tennessee Eastman benchmark process using dynamic principal components analysis based on decorrelated residuals (DPCA-DR)[J]. Chemom. Intell. Lab. Syst., 2013, 125(7): 101-108.

[10] 韩敏，张占奎. 基于改进核主成分分析的故障检测与诊断方法[J]. 化工学报, 2015, 66(6): 2139-2149. HAN M, ZHANG Z K. Fault detection and diagnosis method based on modified kernel principal component analysis[J]. CIESC Journal, 2015, 66(6): 2139-2149.

[11] 童楚东, 蓝艇, 史旭华. 基于互信息的分散式动态PCA故障检测方法[J]. 化工学报, 2016, 67(10): 4317-4323. TONG C D, LAN T, SHI X H. Fault detection by decentralized dynamic PCA algorithm on mutual information[J]. CIESC Journal, 2016, 67(10): 4317-4323.

[12] LIU Y, ZHANG G, XU B. Compressive sparse principal component analysis for process supervisory monitoring and fault detection[J]. J. Process Control, 2017, 50: 1-10.

[13] GE Z, SONG Z. Distributed PCA model for plant-wide process monitoring[J]. Ind. Eng. Chem. Res., 2013, 52(5): 1947-1957.

[14] TONG C, LAN T, SHI X. Fault detection and diagnosis of dynamic processes using weighted dynamic decentralized PCA approach[J]. Chemom. Intell. Lab. Syst., 2017, 161: 34-42.

[15] TONG C, SONG Y, YAN X. Distributed statistical process monitoring based on four-subspace construction and Bayesian inference[J]. Ind. Eng. Chem. Res., 2013, 52(29): 9897-9907.

[16] JIANG Q, WANG B, YAN X. Multiblock independent component analysis integrated with Hellinger distance and Bayesian inference for non-Gaussian plant-wide process monitoring[J]. Ind. Eng. Chem. Res., 2015, 54(9): 2497-2508.

[17] DOWNS J J, VOGEK E F. A plant-wide industrial process control problem[J]. Comput. Chem. Eng., 1993, 17(3): 245-255.

[18] YIN S, DING S X, HAGHANI A,. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process[J]. J. Process Control, 2012, 22: 1567-1581.

[19] QIN S J. Statistical process monitoring: basics and beyond[J]. J. Chemom., 2003, 17(7/8): 480-502.

[20] GE Z, ZHANG M, SONG Z. Nonlinear process monitoring based on linear subspace and Bayesian inference[J]. J. Process Control, 2010, 20(5): 676-688.

[21] GE Z, SONG Z. Multimode process monitoring based on Bayesian method[J]. J. Chemom., 2009, 23(12): 636-650.

[22] LI N, YANG Y. Ensemble kernel principal component analysis for improved nonlinear process monitoring[J]. Ind. Eng. Chem. Res., 2015, 54(1): 318-329.

[23] GE Z, SONG Z. Bayesian inference and joint probability analysis for batch process monitoring[J]. AIChE J., 2013, 59(10): 3702-3713.

[24] HUANG J, YAN X. Dynamic process fault detection and diagnosis based on dynamic principal component analysis, dynamic independent component analysis and Bayesian inference[J]. Chemom. Intell. Lab. Syst., 2015, 148: 115-127.

[25] 杨健, 宋冰, 谭帅, 等. 时序约束NPE算法在化工过程故障检测中的应用[J]. 化工学报, 2016, 67(12): 5131-5139. YANG J, SONG B, TAN S,. Time constrained NPE for fault detection in chemical processes[J]. CIESC Journal, 2016, 67(12): 5131-5139.

[26] SEVERSON K, CHAIWATANODOM P, BRAATZ R D. Perspectives on process monitoring of industrial systems[J]. Annu. Rev. Control, 2016, 42: 190-200.

[27] ZHANG H, QI Y, WANG L,. Fault detection and diagnosis of chemical process using enhanced KECA[J]. Chemom. Intell. Lab. Syst., 2017, 161: 61-69.

[28] BERNAL-DE-LAZARO J M, LLANES-SANTIAGO O, PRIETO-MORENO A,. Enhanced dynamic approach to improve the detection of small-magnitude faults[J]. Chem. Eng. Sci., 2016, 14: 166-179.

[29] 薄翠梅, 韩晓春, 易辉. 基于聚类选择k近邻的LLE算法及故障检测[J]. 化工学报, 2016, 67(3): 925-930. BO C M, HAN X C, YI H,. Neighborhood selection of LLE based on cluster for fault detection[J]. CIESC Journal, 2016, 67(3): 925-930.

Variable weighted principal component analysis algorithm and its application in fault detection

LAN TingTONG ChudongSHI Xuhua

(Faculty of Electrical Engineering & Computer Science, Ningbo University, Ningbo315211, Zhejiang, China)

Traditional principal component analysis (PCA) algorithm, targeting to explore correlations among measured variables in training dataset, has been intensively investigated and applied to data-driven fault detection. However, all variables are considered equally important in modeling process of traditional PCA-based methods, the difference between variable correlations cannot be comprehensively described. A variable weighted PCA (VWPCA) algorithm was proposed and applied to fault detection. Weight calculations were performed on the training dataset so correlation differences among measured variables were fully reflected in the processed data and a distributed PCA-based fault detection model was constructed. When implemented in online fault detection, the Bayesian inference was used to combine multiple monitoring results into an ensemble of probability indices. VWPCA approach assigned different weights to different variables according to the correlation difference, thus PCA modeling took correlation difference into account and the models could completely describe characteristics of the training dataset. Finally, superiority of the proposed VWPCA method was validated by well-known TE process.

principal component analysis；process systems；process control；fault detection

10.11949/j.issn.0438-1157.20170281

TP 277

A

0438—1157（2017）08—3177—06

蓝艇（1976—），男，博士，讲师。

国家自然科学基金项目（61503204）；浙江省自然科学基金项目（Y16F030001）；宁波市自然科学基金项目（2016A610092）。

2017-03-22收到初稿，2017-04-11收到修改稿。

2017-03-22.

LANTing, lanting@nbu.edu.cn

supported by the National Natural Science Foundation of China (61503204), the Natural Science Foundation of Zhejiang Province(Y16F030001) and the Natural Science Foundation of Ningbo (2016A610092).