有界单连通区域上解析逆紧映射的拓扑度

戴作科,董新汉

(湖南师范大学数学与计算机科学学院，中国 长沙 410081)

有界单连通区域上解析逆紧映射的拓扑度

戴作科,董新汉

(湖南师范大学数学与计算机科学学院，中国 长沙 410081)

设Ω和G都是边界局部连通的有界单连通区域，假设f是Ω到G的解析逆紧映射. 通过将单连通区域提升至单位圆盘，本文得到了G的边界点的分支数和其逆象点分支数之间的等式关系，并讨论了f的拓扑度和逆象点个数之间的不等式关系.

割点；拓扑度；分支数

AbstractLettingΩandGbe two simply connected domains with locally connected boundary, lettingfbe a proper holomorphic mapping fromΩontoG, and liftingΩandGonto unit discs, in this work, we have obtained the equality relationship between component numbers of the point on ∂Gand those of its different inverse image points on ∂G. The inequality relationship between the topological degree offand the number of the different inverse image points is also obtained and discussed.

Keywordscut point; topological degree; component number

假设X和Y是两个拓扑空间，令Ω和G分别为X和Y中的两个子集，f:Ω→G为一个连续映射，如果G中每个紧子集的逆象集都是Ω中的紧集，则称f是Ω到G的逆紧映射[1]. 在分形几何与复分析的交叉研究中[2-6]，Cantor边界性质的专题研究必须借助全纯逆紧映射的性质. 对一般解析函数(非逆紧)，其定义域边界的象集分全平面C为若干个连通分支，则相关连通分支的个数、拓扑度和判别点个数又紧密联系着. 著名的Riemann-Hurwitz公式阐述了这个联系[7]. 为了更深入揭示Cantor边界性质中Cantor集C的性质，我们需要边界上割点的重数[8]和连通分支上的拓扑度之间的联系. 本文的目的就是刻画这种联系，至于它的应用我们将另文给出.

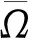
引理1[2-3]令f∈A(Ω)且f:Ω→f(Ω)是逆紧的，则存在k>0使得对于任意w∈f(Ω)都有

nf(w,Ω)≡k.

我们称上述引理中的k为映射f的拓扑度.

引理2[2-3]设f是一个在D内解析的函数. 如果f满足f(D)=D和nf(w,D)≡k<∞，∀w∈D,则f是一个拓扑度为k的有限Blaschke乘积，即

其中zn∈D，β为实数. 此外，f′(z)在D中有k-1个零点(按重数计算)，当|z|=1时，f′(z)≠0；当|w|=1时，nf(w,∂D)=k.

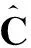
由定义1及割点的定义可知，当且仅当αE(a)>1时，a为E的割点.

1 主要结论

解析逆紧映射的拓扑度由象区域边界点的逆象点个数决定.

定理1设Ω和G都是边界局部连通的有界单连通区域，f∈A(Ω)是一个从Ω到G上的逆紧映射.设w0∈∂G不是∂G的割点，令

f-1({w0})={z0,z1,…,zk-1},

其中zi(i=0,1,…,k-1)互不相同. 如果每个zi都不是∂Ω的割点，则f的拓扑度为k.

证由于f的拓扑度为一常数，不妨设为m，下面证明m=k.

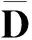
f-1({w0})={z0,z1,…,zk-1}，

可知ai(i=0,1,…,k-1)是∂D上满足f(φ(ai))=w0的k个不同点.

考虑映射h(η)=ψ-1(f(φ(η)))，η∈D. 由引理2可知，h是一个拓扑度为m的有限Blaschke乘积，且对任意|ξ|=1有nh(ξ,∂D)=m，可以断言，ai(i=0,1,…,k-1)是仅有的k个不同的使得h(ai)=ξ0成立的点. 事实上，假如∂D上还存在不同于ai(i=0,1,…,k-1)的点b满足h(b)=ξ0，则有

ψ(h(b))=ψ(h(ai))=ψ(ξ0)=w0，

从而

f(φ(b))=ψ(h(b))=ψ(h(ai))=w0=f(φ(ai))

成立，故b必然等于某个ai. 由此可以得出m=k且h是一个拓扑度为k的有限Blaschke乘积，即f的拓扑度为k.

解析逆紧映射象区域边界点的分支数和其逆象点的分支数之间有很好的对应关系. 在下面的引理中cardA表示A中不同元素的个数.

引理3设G是一个边界局部连通的有界单连通区域，f是一个从D到G上的共形映射. 令a∈∂G且

A=f-1({a})={ζ∈∂D:f(ζ)=a},m=cardA≤∞.

则有m=α∂G(a)成立.

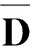
引理4设G是一个边界局部连通的有界单连通区域，f∈A(D)是一个拓扑度为k的从D到G上的逆紧映射. 令a∈∂G且有

A=f-1({a})={ζ∈∂D:f(ζ)=a},m=cardA≤∞.

则m=kα∂G(a)成立.

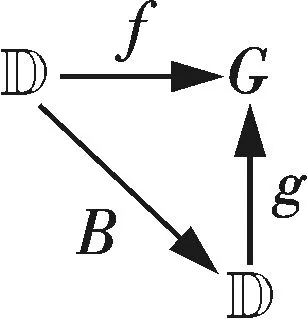
令m′=cardC，其中

C=g-1({a})={ζ∈∂D:g(ζ)=a}.

由引理3，m′=α∂G(a)成立.

下面证明f-1({a})=B-1(g-1({a})). 任取z0∈f-1({a})，有f(z0)=a，故B(z0)=g-1(f(z0))=g-1({a})，从而有z0∈B-1(g-1({a}))，因此f-1({a})⊆B-1(g-1({a})). 再任取z1∈B-1(g-1({a}))，有B(z1)∈g-1({a})，即g-1(f(z1))∈g-1({a})，故有f(z1)=a，即z1∈f-1({a})，这说明B-1(g-1({a}))⊆f-1({a}).

综合以上可知f-1({a})=B-1(g-1({a})).

由于B是拓扑度为k的有限Blaschke乘积，由引理2可知card(B-1(C))=kcardC，所以m=kα∂G(a)成立.

定理2设Ω和G都是边界局部连通的有界单连通区域，f∈A(Ω)是一个拓扑度为k的从Ω到G上的逆紧映射. 令w0∈∂G且

f-1({w0})={z0,z1,…,zq-1},

其中zi(i=0,1,…,q-1)互不相同. 我们有

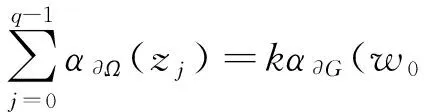
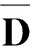
因为f∘g1=g2∘B，且都是拓扑度为k的解析逆紧映射，由引理3和引理4可知

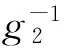
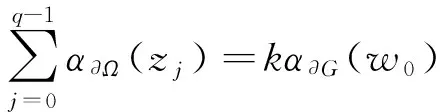
推论1设Ω和G都是边界局部连通的有界单连通区域，f∈A(Ω)是一个拓扑度为k的从Ω到G上的逆紧映射. 若w0∈∂G不是∂G的割点且有

f-1({w0})={z0,z1,…,zq-1}，

其中zi(i=0,1,…,q-1)互不相同，则有q≤k，且“=”成立的充分必要条件是每个zj都不是∂Ω的割点.

证因为α∂Ω(zj)≥1且α∂G(w0)=1，由定理2可知

显然“=”成立的充分必要条件是每个zj都不是∂Ω的割点.

推论2设Ω和G都是边界局部连通的有界单连通区域，f∈A(Ω)是一个拓扑度为k的从Ω到G上的逆紧映射. 若w0∈∂G是∂G的割点且有

f-1({w0})={z0,z1,…,zq-1}，

其中zi(i=0,1,…,q-1)互不相同，如果每个zj都不是∂Ω的割点，则有q≥2k.

证由割点的定义，我们有α∂G(w0)≥2和α∂Ω(zj)=1. 再由定理2可知

即q≥2k成立.

[1] RUDIN W. Function theory in the unit ball ofCn[M]. New York: Springer Verlag, 1980.

[2] DONG X H, LAU K S. Cantor boundary behavior of analytic functions. Recent development in fractals and related fields[J]. Birkhäuser, 2010,232(1):283-294.

[3] DONG X H, LAU K S, LIU J C. Cantor boundary behavior of analytic functions[J]. Adv Math, 2013,232(1):543-570.

[4] DONG X H, LAU K S, WU H H. Cauchy transform of self-similar measures: Starlikeness and univalence[J]. Trans Am Math Soc, 2017,369(7):4817-4842.

[5] DONG X H, LAU K S. Cauchy transforms of self-similar measures: the Laurent coefficients[J]. J Funct Anal, 2003,202(1):67-97.

[6] DONG X H, LAU K S. An integral related to the Cauchy transform on the Sierpinski gasket[J]. Exp Math, 2004,13(4):415-419.

[7] TEINMETZ N S. The formula of Riemann-Hurwitz and iteration of rational functions[J]. Complex Variables Theory Appl, 1993,22(3):203-206.

[8] POMMERENKE C. Boundary behaviour of conformal maps [M]. New York:Springer Verlag, 1992.

(编辑 HWJ)

重要启事

“优先数字出版”是以纸质版期刊录用稿件为出版内容，先于纸质期刊出版日期出版的数字期刊出版方式．我刊已于2012年起与中国学术期刊(光盘版)电子杂志社签订了优先数字出版协议．凡被我刊录用的稿件一经优先数字出版，读者即可在中国知网(CNKI)全文数据库进行检索和下载．凡向本刊投稿的作者，如无特别申明，均被视为作者授权本刊编辑部在纸质期刊出版前，可以在中国学术期刊(光盘版)电子杂志社主办的“中国知网”(www.cnki.net)上优先数字出版；也被视为作者同意并授权我刊与其他电子杂志社签订的协议，并许可其在全球范围内使用该文的信息网络传播权、数字化复制权、数字化汇编权、发行权及翻译权，并不再额外支付稿酬．

本刊编辑部

Topological Degree of Proper Holomorphic Mapping on Bounded Simply Connected Domains

DAIZuo-ke,DONGXin-han*

(College of Mathematics and Computer Science, Hunan Normal University, Changsha 410081, China)

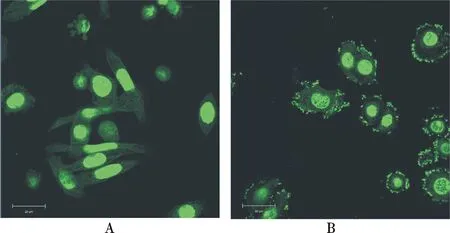
图1 跨界基因沉默菌株侵染细胞的吖啶橙染色图(P.34) Fig.1 Acridine orange staining showed that the Tk-RNAi bacteria invaded into mammalian cells(P.34)

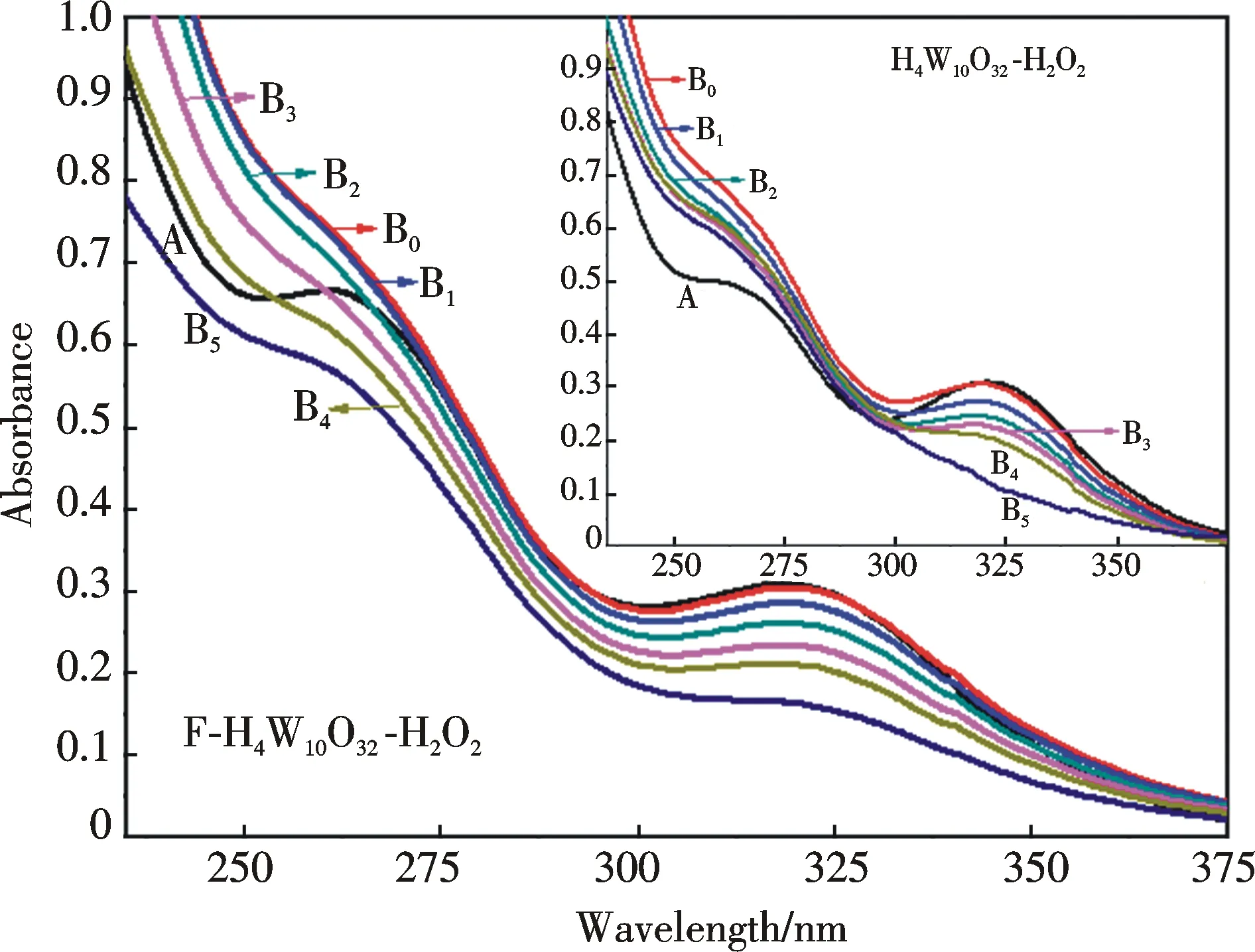
Fig.2 The UV spectra (200～375 nm) of F-H4W10O32(8.49×10-5 mol/L) in water containing H2O2. (A) The system in a pure water (0.1 mL),(B0)Adding 0.2 mol/L H2O2(0.1 mL) to the system A, (B1→B5 ) After the system was irradiated using UV light for 10, 30, 40, 50 and 80 min. Inset is the UV spectra (200～375 nm) of H4W10O32 in water containing H2O2 under the same conditions(P.66)

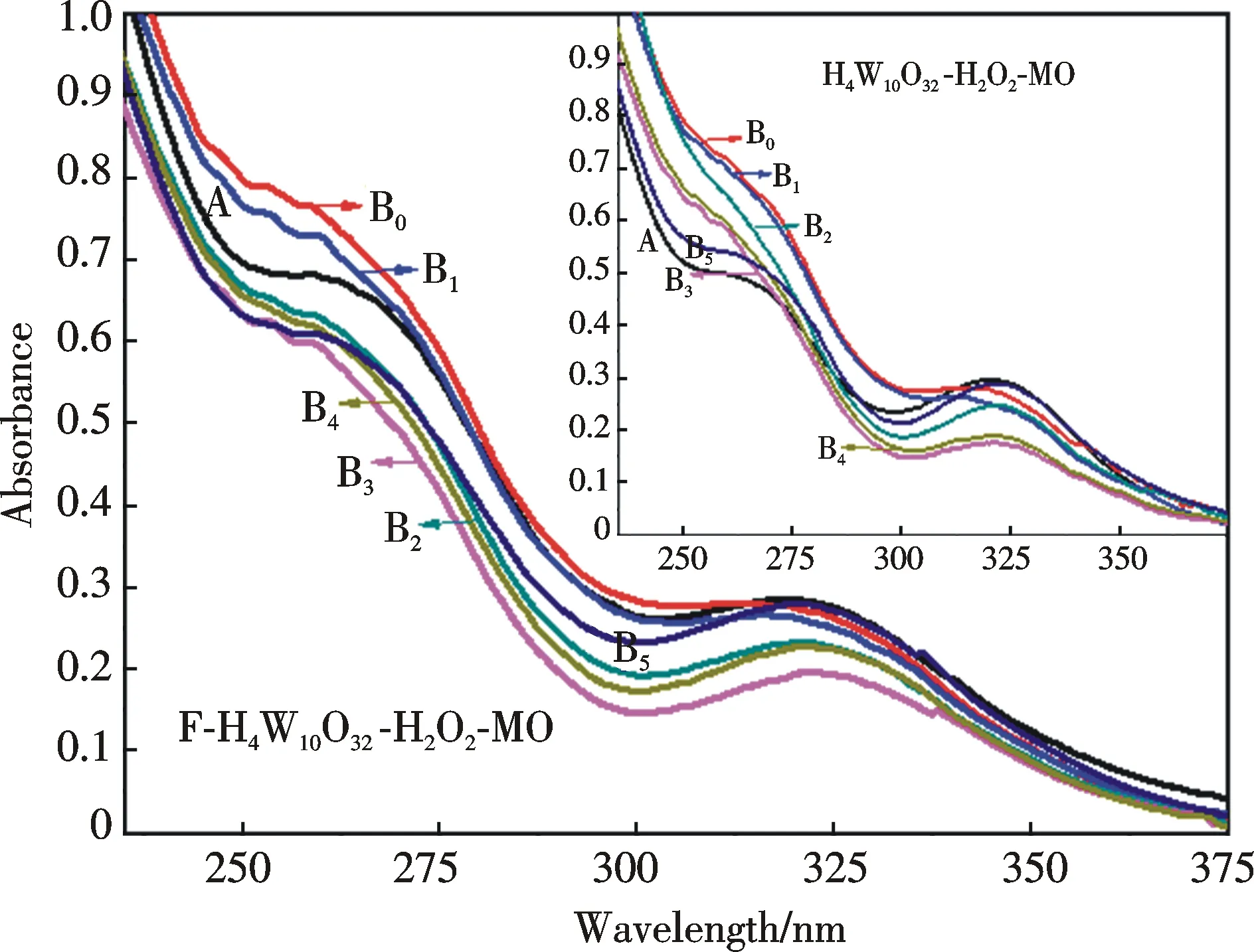
Fig.3 The UV spectra (200～375 nm) of F-H4W10O32(8.49×10-5 mol/L) in water containing H2O2 and MO. (A) The system in a pure water (0.2 mL),(B0)Adding 0.2 mol/L H2O2(0.1 mL) and 2.5 mg/L MO (0.1 mL) to the system A, (B1→B5 ) After the system was irradiated using UV light for 10, 20, 40, 50 and 80 min. Inset is the UV spectra (200～375 nm) of H4W10O32 in water containing H2O2 and MO under the same conditions(P.66)

G420; O174.5

A

1000-2537(2017)05-0077-03

2017-01-09

国家自然科学基金资助项目(11571099);高等学校博士学科点专项科研基金资助项目(20134306110003)；湖南省教育厅科研资助项目(14K057)

*通讯作者,E-mail：xhdong@hunnu.edu.cn

10.7612/j.issn.1000-2537.2017.05.011