空投装备缓冲气囊匹配设计与仿真计算研究

洪煌杰，王红岩，李建阳，吕哲源，芮强



空投装备缓冲气囊匹配设计与仿真计算研究

洪煌杰1，王红岩2，李建阳3，吕哲源2，芮强2

（1.工程兵科研一所，江苏 无锡 214035；2.装甲兵工程学院 机械工程系，北京 100072；3.装备学院 昌平士官学校，北京 102249）

目的解决缓冲气囊的研制周期长、成本高而设计效果却不够理想的问题。方法针对这个问题，对缓冲气囊的着陆缓冲过程进行解析建模，然后通过参数的无量纲化，将缓冲气囊的解析计算模型转化成无量纲动力学模型。借助缓冲气囊参数匹配图，根据试验需求对气囊缓冲系统进行匹配设计，然后采用有限元方法对气囊缓冲系统进行建模分析。结果搭建了气囊跌落缓冲试验系统，进行了气囊跌落缓冲试验，通过试验验证了参数匹配方法的有效性，并利用试验数据对有限元仿真计算结果进行了验证，配重平台最大加速度和气囊最大压强的误差分别为1.6%和3.1%。结论有限元仿真的精度可以满足分析要求，基本反映了实际的气囊缓冲特性。

缓冲气囊；参数匹配图；有限元方法；跌落缓冲试验

由于缓冲气囊具有缓冲效果好、结构简单、质量轻、折叠体积小、可回收利用、成本低廉等优点，在装备空投中得到了广泛的应用。我国主要经过反复的跌落试验来确定缓冲气囊参数，使得缓冲气囊的研制周期长、成本高而设计效果却不够理想。如果能在初始设计时计算出缓冲气囊参数的匹配范围，并对设计的缓冲气囊进行仿真分析，就能有效减少跌落试验次数，提高缓冲气囊设计效率和匹配成功率。因此，有必要对缓冲气囊匹配设计与仿真计算方法进行研究，使缓冲气囊能较好地保护装备。

最早对缓冲气囊的研究是从试验研究开始的，通过以投放为主的试验研究气囊缓冲性能，检验气囊缓冲系统是否有效。Wright-Patterson空军基地对三种桶型缓冲气囊进行了试验测试，对缓冲效果进行评估与对比，并通过35次圆柱形缓冲气囊的投放试验得到变排气孔面积缓冲气囊比固定排气孔面积缓冲气囊缓冲效率高的结论[1—2]。为了更方便快捷地研究气囊的缓冲特性，国内外专家学者采用解析方法建立了缓冲气囊的解析分析模型，对缓冲气囊进行了大量的研究。北京航空航天大学的杨春信等人基于热力学方法建立了气囊缓冲过程仿真模型，并且考虑了在实际缓冲过程中缓冲气囊的压缩变形情况和排气孔面积大小的变化，仿真计算了缓冲过程中的最大过载、缓冲时间等缓冲特性[3]。有限元技术随着计算技术的发展在气囊缓冲特性分析中被广泛地采用。美国的Taylor采用显式有限元方法对重装空投的气囊缓冲技术进行了仿真分析[4]。湖南大学的文桂林等人建立了双气室新型缓冲气囊的有限元模型，并以气囊体积为优化目标，对气囊的设计参数进行了优化设计[5]。从国内外的研究现状来看，对气囊缓冲技术的研究主要采用三种方法：试验方法、解析方法和有限元方法。试验方法能最直接和最真实地反映气囊缓冲特性，但是对于大型装备缓冲气囊的试验测试难度大、重复性差、成本高、周期长、安全性低，而且有些极端工况无法通过试验来实现。解析方法是通过分析缓冲气囊压缩过程中内部气体参数的变化规律来研究气囊缓冲特性，该方法简便易行，计算精度能满足一般工程需要，但无法准确计算缓冲气囊的变形。有限元方法通过对缓冲气囊划分网格，计算缓冲气囊压缩过程中任意时刻的变形，以及变形引起的内部气体参数的变化。该方法建模复杂、运算量大，但是计算较准确，可以模拟缓冲气囊的变形情况，而且可以计算在特殊着陆工况下气囊的缓冲特性。

文中基于解析方法对空投装备的缓冲气囊参数进行匹配设计，并建立气囊缓冲系统的有限元模型进行仿真计算，然后采用试验数据对模型进行验证。

1 缓冲气囊参数匹配方法

1.1 着陆缓冲过程的解析计算模型

装备经过空投着陆，缓冲气囊首先着地并被迅速压缩，缓冲气囊内气体压强升高，从而产生内外压差，使装备减速，起到缓冲作用。排气孔在满足条件时开启，缓冲气囊开始向外排气，以防止内部压力过高，装备仍继续下落，直至完成整个工作过程[6]。

缓冲气囊着陆缓冲过程的解析建模一般采用以下假设[7—8]：

1）缓冲气囊内气体遵从理想气体状态方程。

2）由于气囊壁导热较差，而且着陆缓冲过程时间极短，认为着陆缓冲过程为绝热压缩过程。

3）由于缓冲气囊内各处气体压强相差不大，假设缓冲气囊内各处气体压强始终处处相等。

4）由于气囊壁漏气量极小，假设缓冲气囊内气体仅从排气孔流出。

5）在低速情况下气动阻力极小，可以忽略不计。

根据上述假设，可以将单个缓冲气囊简化为类似汽缸的容器。

着陆缓冲过程装备受到缓冲气囊内气体压力、大气环境压力和重力的作用，因此装备的平衡方程为：

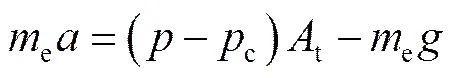
式中：e为装备质量；为装备加速度；为气囊压强；c为大气环境压强；t为装备底部与缓冲气囊顶部的接触面积；为重力加速度。

缓冲气囊内任意时刻气囊压强为：

式中：0为气囊初始压强；为气囊内气体质量；0为气囊内气体初始质量；为气囊内气体体积；0为气囊内气体初始体积。

缓冲气囊通过排气孔排气的过程可以近似为气体压缩经薄壁小孔排出，是可压缩流体的绝热流动[9]。

式中：为比热比；为流量系数；v为排气孔面积；为气体常数；0为缓冲气囊内气体初始温度。

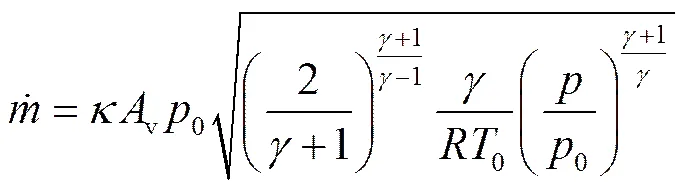
在临界流动状态下，气囊压强继续增加时，排气孔处气体流速仍为声速，排气孔处气体压强v等于临界压强cr，大于大气环境压强c，存在着一个压差，即排气孔外存在一个扰动。因为此时排气孔处气体流速已达声速，扰动不能穿越声速面，所以不能影响排气孔处气体的流动，此时排气孔处气体的状态称为超临界状态[10]。气流自排气孔流出后，遇到低压气流将会继续膨胀，使压强由排气孔处的临界压强降低到大气环境压强。此时的排气孔流量公式仍为式（4）。

1.2 无量纲动力学模型

缓冲气囊参数匹配是通过缓冲气囊参数（包括气囊尺寸和排气孔面积）的组合搭配使气囊缓冲性能满足实际要求。在参数的组合搭配中，由于各个参数量纲不同而不便于计算分析，因此，在缓冲气囊参数匹配中可以进行无量纲化处理。这样使得运算更为简单，进行数值计算更为方便，便于进行数学处理。

在对缓冲气囊的计算中，排气孔流量大小与任意时刻缓冲气囊内气体减少的质量相等，即：

式中：v为排气孔处气体密度；b为气囊底面积。

式中：c为大气环境密度；为气囊内外压强比。

式中：为时间因子；为气囊剩余高度比；0为着陆初速度。

式中：c为大气环境温度。

式中：为排气孔面积因子；，，为以为自变量的函数。

(11)

式中：为气囊高度因子；为物体质量因子。

1.3 缓冲气囊参数匹配范围

在无量纲动力学模型中，物体质量因子、气囊高度因子和排气孔面积因子为三个最主要的输入参量，根据设计要求则可以得到最大加速度因子max、着陆末速度比1和缓冲时间因子1。对于最大加速度因子，为满足减速要求，最大加速度应大于一定值，而为控制冲击，最大加速度不应过大，因此一般应在4~20之间，即4≤max≤20。对于着陆末速度比，通常着陆末速度应不超过着陆初速度的一半，即1≤0.5。对于缓冲时间因子，一般有1≤3。

对于给定的物体质量因子，将不同气囊高度因子和排气孔面积因子的组合输入无量纲动力学仿真模型进行求解计算，可以求得坐标图区域相应的最大加速度因子、着陆末速度比和缓冲时间因子，可在同一坐标图中标示出最大加速度因子、着陆末速度比和缓冲时间因子的等值曲线。当最大加速度因子、着陆末速度比和缓冲时间因子均在限定范围内时，由边界等值曲线围成的坐标图区域为缓冲气囊参数匹配范围，此图为缓冲气囊参数匹配图。物体质量因子为16.78时的缓冲气囊参数匹配如图1所示。

对于给定的物体质量，可以从缓冲气囊参数匹配范围中选取合适的气囊高度因子和排气孔面积因子的组合，然后转化为实际尺寸的气囊高度和排气孔面积。图1中所标五角星为某型空投装备缓冲气囊的参数组合位置，可以看出该参数组合位置位于缓冲气囊参数匹配范围中，但着陆末速度偏大，较可能与地面产生较大冲击，若设置较严格的边界条件如1≤0.4，该参数组合将位于缓冲气囊参数参数匹配范围外。

图1 W为16.78时的缓冲气囊参数匹配

2 气囊缓冲系统设计与有限元建模

2.1 气囊缓冲系统设计

根据缓冲气囊参数匹配方法设计一套满足小质量配重跌落缓冲要求的缓冲气囊系统。设定环境压力为标准大气压（101 325 Pa），温度为293.15 K，总配重质量为440 kg，着陆初速度为6 m/s，要求着陆末速度不大于2 m/s，着陆缓冲过程冲击加速度不大于15。在上述条件下对气囊缓冲系统进行设计。

为保证气囊缓冲系统的稳定性，气囊缓冲系统由四个独立、相同的缓冲气囊组成，对称分布地连接于配重下方。每个缓冲气囊均为长方体形充气式缓冲气囊，缓冲气囊上开设进气孔和排气孔。进气孔设于缓冲气囊顶部，通过配重上安装的进气阀由气瓶充气。排气孔由圆形钢圈与爆破膜组成，设于缓冲气囊外侧面中部。

假定缓冲气囊与配重接触面积c为900 mm×360 mm，结合单气囊配重质量110 kg，可以由物体质量因子公式得到物体质量因子为30.45。根据缓冲气囊参数匹配方法可以得到物体质量因子为30.45时的缓冲气囊参数匹配图，如图2所示。

图2 W为30.45时的缓冲气囊参数匹配

参考着陆末速度不大于2 m/s，着陆缓冲过程冲击加速度不大于15的设计要求，并以0.8的安全系数考虑，所需求的缓冲气囊参数匹配区域为由max=4，max=12，1=0.3以及1=3四条等值曲线包围而成的区域。在该区域中选取=0.1143，=0.8785的参数组合，如图3中的五角星位置，该位置点的参数组合满足设计要求。

由于缓冲气囊外侧面的排气孔由圆形钢圈与爆破膜组成，为防止配重与圆形钢圈在着陆缓冲过程中的碰撞，缓冲气囊外侧应超出配重侧面。因此缓冲气囊的底面积b应大于缓冲气囊与配重的接触面积c，设计为900 mm×480 mm。根据气囊高度因子与排气孔面积因子的公式，可以得到气囊高度0与排气孔面积v，如式（13）和式（14）所示。

(14)

因此通过缓冲气囊参数匹配可以得到气囊尺寸为900 mm×480 mm×420 mm，排气孔直径为100 mm。

2.2 缓冲气囊有限元建模

缓冲气囊的有限元建模中最早使用且最常用的方法是控制体积法[11]。控制体积法将缓冲气囊定义为不断变化的控制体积，如图3所示。与解析方法相同，控制体积法假设控制体积内的气体为理想气体，且与外部环境没有热交换，在任意时刻控制体积内各处的压强和温度是均一的。控制体积内的气体状态方程与解析方法是一致的。

图3 控制体积法

控制体积法中控制体积为控制表面包围的体积，控制表面则由气囊织物进行网格划分所得到的壳单元组成。在时刻，缓冲气囊的控制体积可以由气囊壁单元的位置、方向和表面积通过格林定理计算得到，即：

将时刻缓冲气囊内气体的均匀压力作用于气囊壁内表面，结合其他受力条件，可以计算得到缓冲气囊的变形。根据变形情况又可以计算出下一时刻缓冲气囊的控制体积。

文中研究气囊缓冲系统的着陆缓冲过程，对于空投前缓冲气囊的折叠状态与空投过程中缓冲气囊的展开过程不予考虑，只需建立已展开状态的缓冲气囊。实际的缓冲气囊含有进气孔和排气孔，但格林定理的应用需采用闭合表面，所以将孔洞处理为有限元单元，使单个缓冲气囊的有限元模型为封闭的模型，各面壳单元的法向方向均指向缓冲气囊外侧。划分有限元网格后的气囊缓冲系统如图4所示。

图4 配重平台-气囊缓冲系统的有限元模型

2.3 接触模型

接触和碰撞问题是一个典型且复杂的非线性力学问题，经常同时涉及到材料非线性、几何非线性和状态非线性三种非线性[12]。接触和碰撞问题的复杂主要在于接触碰撞中，边界条件不但是未知的，而且是不断变化的，需要在计算求解过程中确定，接触力的法向分量只能是压力、接触界面的摩擦条件和接触物体不可相互侵入这一些接触条件更是有别于普通约束条件。气囊缓冲系统在着陆缓冲过程中正存在这样的接触和碰撞问题，对接触模型的定义显得尤为重要。

由于缓冲气囊被固定在装备下面，假设装备与气囊缓冲系统上表面的连接是完全固定的，相互之间无滑动，可以采用绑定接触[13]对其进行描述。从严格意义上讲，绑定接触更大程度上是一种节点运动约束。装备底部定义为主表面，气囊缓冲系统上表面定义为从表面。从表面上的一系列从节点被刚性连接到主表面上。从节点的力和力矩被转移到主表面上，并根据主表面的运动强制运动，从节点的位移与主表面保持一致。

在着陆缓冲过程中，各个缓冲气囊会发生较大的压缩变形，各个缓冲气囊的不同部分以及邻近的缓冲气囊之间都会发生接触，从而影响缓冲气囊各个时刻的变化形状，进而影响气囊体积、气囊压强以及装备速度。采用点面接触对各个缓冲气囊的不同部分以及邻近的缓冲气囊之间的接触关系进行描述。对于不同的缓冲气囊，缓冲气囊之间互为主从表面。对于同一个缓冲气囊，缓冲气囊的各部分既是主表面又是从表面，其接触又可称为自接触[14]。另外，考虑到缓冲气囊与装备的其他部位可能产生的接触，对缓冲气囊侧面与装备侧面较接近的部位同样定义点面接触，以相对较硬的部分装备侧面为主表面。

上述点面接触采用罚函数法[15]进行求解。采用参考距离用于判断从节点是否与主表面发生接触，一般为主表面占据的厚度空间。当从节点穿透到主表面由参考距离决定大小的空间里，就认为该主表面和该从节点发生了接触，而从节点在参考空间之外时则不做任何处理。一旦接触发生，罚函数法就从发生接触的从节点在主表面的投影点上向该从节点施加一个使从节点向外离开参考空间的法向接触力。这个力的大小与从节点侵入参考空间的深度、主面刚度成正比：

式中：n为法向接触力；为穿透深度；n为主表面的外法线单位矢量；k为主表面的刚度。

3 气囊跌落缓冲试验与验证

3.1 气囊跌落缓冲试验系统

直接进行气囊缓冲系统空投试验的周期长且成本巨大，因此采用根据参数匹配方法设计缓冲气囊，配合小质量配重平台进行缓冲气囊的室内跌落缓冲试验，对仿真建模方法以及缓冲气囊设计方案进行验证。

整个气囊跌落缓冲试验系统由试验对象、悬挂释放装置、试验测试系统以及高速摄像系统四个部分组成。其中试验对象包括气囊缓冲系统和配重平台。

根据缓冲气囊参数匹配得到的气囊尺寸对缓冲气囊进行加工制作。缓冲气囊由两层织物制成，内层材料为涂层锦丝绸，透气量小，主要用于减少缓冲气囊内气体通过气囊壁泄漏。外层材料为锦丝帆绸，强度较大，主要用于使气囊壁能承受较大的压力。缓冲气囊外层缝有加强带，用以加强气囊织物的强度。

配重平台为长方体构型，钢板结构，中心位于平台几何中心。平台设置吊挂装置，通过四条吊绳与吊点连接，吊点在重心上方以保持配重平台姿态平衡。平台底部为长方形平面，连接固定四个均布的缓冲气囊。平台上四角布置并固定配重块，用于配重平台重量的调节。平台上还设有四个进气阀，连接四个缓冲气囊顶部的进气孔，用于分别对四个缓冲气囊充气。

跌落缓冲试验在光线照明充足的室内进行，室内环境为常温常压无风环境。气囊跌落缓冲试验系统各部分连接如图5所示。

图5 气囊跌落缓冲试验系统

3.2 有限元仿真结果验证

采用配重质量为435 kg、着陆初速度为6 m/s、充气情况为基本满的工况进行仿真计算，可以得到配重平台加速度和气囊压强的仿真曲线，并与相同工况的试验曲线进行对比，如图6和图7所示。

可以看出，配重平台加速度和气囊压强的仿真曲线与试验曲线的一致性较好。有限元仿真中配重平台最大加速度和气囊最大压强分别为13.51和0.1315 MPa，其试验值分别为13.30和0.1275 MPa，误差分别为1.6%和3.1%。同样地，对不同配重质量、着陆初速度的工况进行验证，气囊缓冲特性试验各工况误差对见表1。

可以看出各工况的误差很小，有限元仿真的精度可以满足分析要求，基本反映了实际的气囊缓冲特性。仿真的误差的产生主要来自于以下几点。

1）有限元仿真模型经过了一定的简化处理，与实际的配重平台-气囊缓冲系统有一定的差异，且为控制有限元仿真模型的规模，有限元网格划分控制在可接受程度。

2）仿真计算中假设排气孔面积为设计大小，未对可能影响排气孔面积大小的个别情况加以考虑。在试验中可能出现爆破膜未完全冲开的情况，导致排气孔面积大小与设计大小不一致。

3）试验中配重平台-气囊缓冲系统仍存在极小的姿态，不可能与仿真计算一样纯垂直下落，对缓冲气囊的缓冲效果造成一定的影响。

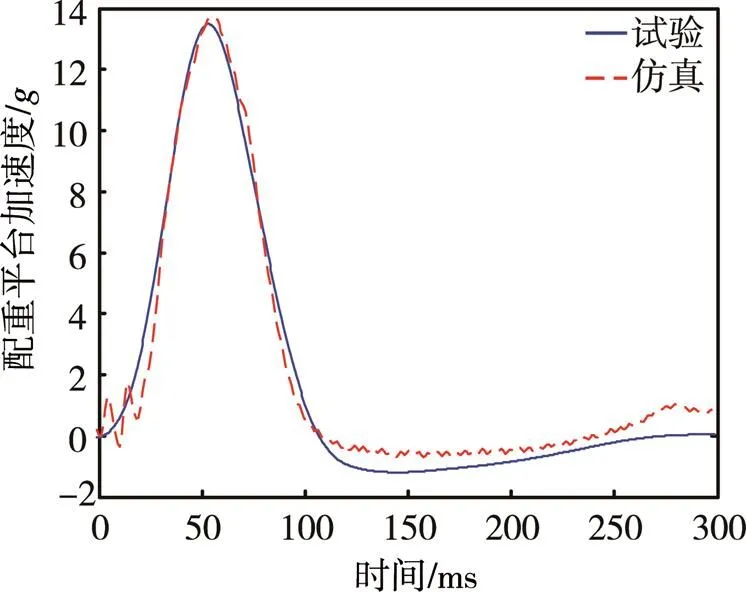
图6 配重平台加速度曲线对比

图7 气囊压强曲线对比

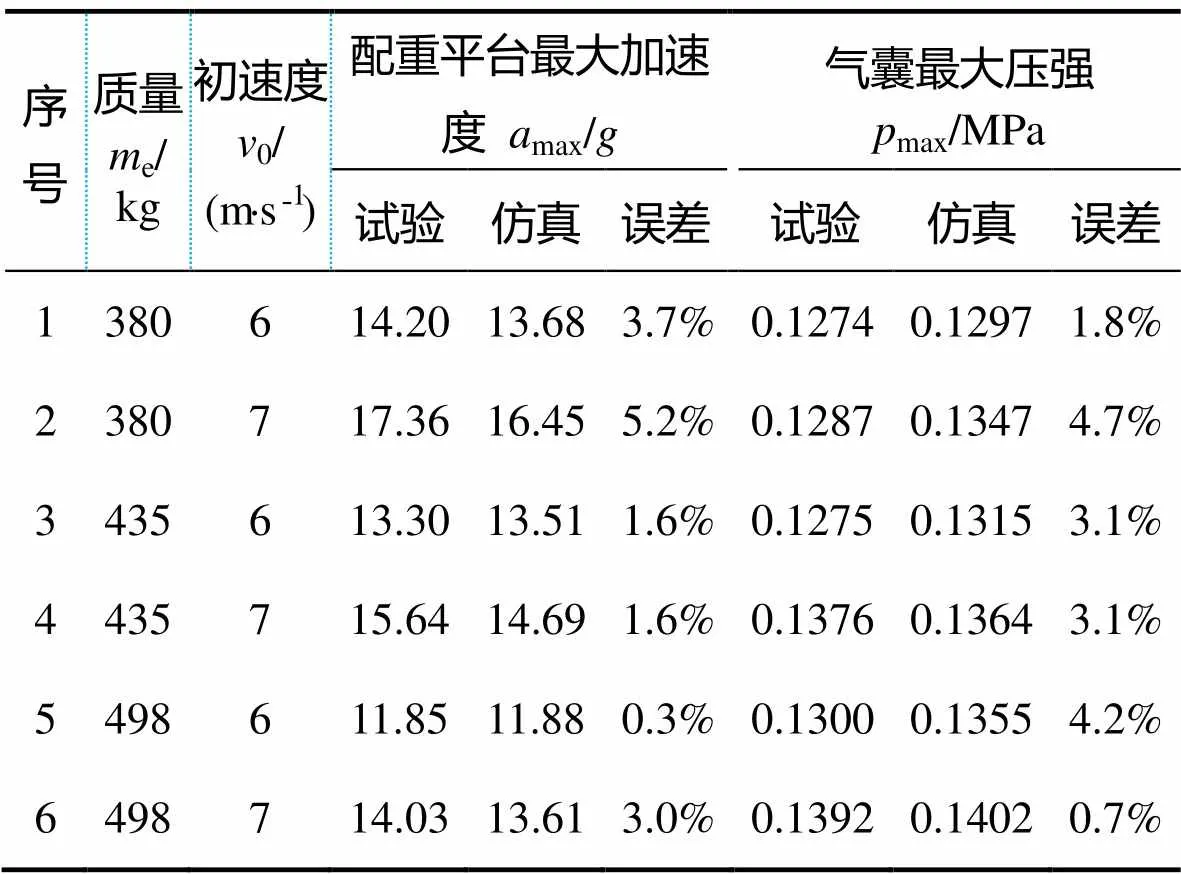
表1 气囊跌落缓冲试验各工况误差

4 结论

1）对缓冲气囊的着陆缓冲过程进行了解析建模，然后通过参数的无量纲化，将缓冲气囊的解析计算模型转化成无量纲动力学模型。借助缓冲气囊参数匹配图，得到适合给定物体质量因子的气囊高度因子和排气孔面积因子的可能参数组合。

2）利用缓冲气囊参数匹配方法，根据试验需求对气囊缓冲系统进行了匹配设计。搭建了气囊跌落缓冲试验系统进行了气囊跌落缓冲试验。

3）进行了气囊缓冲系统的有限元仿真分析。采用有限元方法对气囊缓冲系统进行建模分析，并利用相同工况的试验数据对仿真结果进行了对比验证。结果表明，有限元仿真的精度可以满足分析要求，基本反映了实际的气囊缓冲特性。

[1] MADAFER C. Evaluation of Three Types of Airbag Decelerators by Drop Tests[R]. Ohio: Wright Patterson AFB, 1953.

[2] TOMCSAK S. Decelerator Bag Study[R]. Ohio: Wright Patterson AFB, 1960.

[3] 王亚伟, 杨春信, 柯鹏, 等. 货台空投系统气囊缓冲过程仿真[J]. 系统仿真学报, 2007, 19(14): 3176—3179.

[4] [4] ANTHONY P T. Investigation of the Application of Airbag Technology to Provide a Softlanding Capability for Military Heavy Airdrop[J]. AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, 2016, 16: 2001—2045.

[5] 文桂林, 乐永祥, 尹汉锋, 等. 双气室缓冲气囊多学科设计优化[J]. 湖南大学学报(自然科学版), 2010, 37(7): 27—31.

[6] 李建阳, 王红岩, 芮强, 等. 自充气式气囊缓冲特性试验研究[J]. 振动与冲击, 2014, 33(4): 119—123.

[7] 李建阳, 王红岩, 芮强, 等. 空投缓冲气囊有限元模型修正方法[J]. 兵工学报, 2015, 36(4): 752—757.

[8] ZHANG Jun-yuan, JIN Yang, XIE Li-zhe, et al. Establishment and Validation for the Theoretical Model of the Vehicle Airbag[J]. Chinese Journal of Mechanical Engineering. 2015, 28(3): 487—495.

[9] 罗惕乾. 流体力学[M]. 北京: 机械工业出版社, 2003.

[10] 何立明, 赵罡, 程邦勤. 气体动力学[M]. 北京: 国防工业出版社, 2009.

[11] WANG J T, NEFSKE J. A New CAL3D Airbag Inflation Model [R]. SAE Paper No 880654, 1988.

[12] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.

[13] 欧贺国, 方献军, 洪清泉. RADIOSS理论基础与工程应用[M]. 北京: 机械工业出版社, 2013.

[14] 马志雄. 轿车台车试验方法及侧面约束系统数学仿真技术研究[D]. 武汉: 武汉理工大学, 2008.

[15] WANG Hong-yan, HONG Huang-jie, HAO Gui-xiang, et al. Characteristic Verification and Parameter Optimization of Airbags Cushion System for Airborne Vehicle[J]. Chinese Journal of Mechanical Engineering, 2014, 27(1): 50—57.

Matching Design and Simulating Calculation of Airbag for Airdropping Equipment

HONG Huang-jie1, WANG Hong-yan2, LI Jian-yang3, LYU Zhe-yuan2, RUI Qiang2

(1.Wuxi First Research Institute, Wuxi 214035, China; 2.Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China; 3.Academy of Equipment, Beijing 102249, China)

Objective To solve the problem of long development cycle, high cost and unsatisfactory design effect of airbag. Methods In view of this problem, the cushioning process of airbag was modeled by analytical method. Through the non dimensional parameters, the analytical model was transformed into a non dimensional dynamical model. By means of the airbag parameter matching chart, the airbag cushion system was designed for matching based on test requirement. Then the model of airbag cushion system was established and analyzed by the Finite Element Method. Results The airbag cushion test system was built to carry out the drop test. The parameter matching method and simulation result were validated by the drop test. The error of maximum acceleration of counterweight platform and Maximum pressure of airbag were 1.6% and 3.1% respectively. Conclusion The accuracy of the finite element simulation can meet the analysis requirements, basically reflects the accrual airbag buffer characteristics.

airbag; parameter matching chart; finite element method; drop test

10.7643/ issn.1672-9242.2017.04.001

TJ02；V244

A

1672-9242(2017)05-0001-07

2016-11-15；

2016-12-23

洪煌杰（1985—），男，福建人，博士，工程师，主要从事工程装备研究。