构建科学取向的数学教学设计能力培养体系

马晓丹，张春莉



构建科学取向的数学教学设计能力培养体系

马晓丹，张春莉

（北京师范大学教育学部，北京 100875）

构建科学取向的数学教学设计能力培养体系的重要意义在于指明数学教学设计能力培养的方向，建立数学教学设计中的三大联系．基于科学取向教学论培养数学教学设计能力，建议从以下4个方面寻求突破：首先，明确科学取向教学论指导数学教学设计的意义；其次，解决数学教师在提升教学设计能力的过程中遇到的困惑；再次，立足学科特点，突出学科特色；最后，基于科学取向教学论实施数学教学设计能力的评价．

科学取向教学论；数学教学设计；教学目标；教学过程；教学评价

教学设计能力是教师专业能力的一个重要组成部分，它是教师在专业活动与行动中表现出的专业品质[1]．教学设计的取向与定位决定了教学设计的路径与结果[2]．数学教学设计能力既包括数学教学设计的观念，还包括数学教学设计的知识与技能[3]．反观中国的数学教学设计，往往表现出各个教学活动之间是割裂的、独立的，若能从数学本质和数学学习心理的角度对接下来的教学活动给出承上启下的阐释，不但能促进教学设计者思考设计该教学环节或教学活动的新课标精神，还能促进教学设计的执行者充分理解并更好地贯彻新课标的理念[4]．进一步来说，若要使数学教学设计有法可依、有据可循，则应当在深入剖析不同学段、不同课型的数学教学设计存在的问题的基础之上，以认知心理学为理论基础，探寻数学教学设计能力培养的途径．正所谓“论立于此，若射之有的也，或百步之外，或五十步之外，的必先立，然后挟弓注矢以从之”．

1 明确当前数学教学设计存在的问题

2016年5月科学取向教学论在中小学学科教学中的应用研究（数学学科）课题组在广州市花都区开展调研工作，面向小学、初中、高中3个学段，搜集新授课、讲练课、复习课的数学教学设计共计70份．课题组对部分教师进行访谈，明确了当前不同学段、不同课型的数学教学设计存在的问题类型：

一是，教学目标模糊，具体表现为目标设置含糊不清，不能清晰地反映出希望学生达成的认知水平，混淆了学生经历或体验的过程与学习之后的学习结果．例如将目标表述为“进一步理解正数和负数的概念”，这里的“进一步理解”指的是“说出正数和负数的定义？”还是指“借助数轴解释正数和负数的含义？”又或是“用正数和负数解释生活中的问题？”可见，原先的表述并不清楚．再如设置诸如“增强观察能力”的目标，这里的“观察能力”究竟是学习结果？还是学习过程？若是学习结果，又该如何观测？若是学习过程，是否想表达学生在观察一段时间之后，能够说出、写出或画出具体的数学对象？显然，用“增强观察能力”来设置目标，对教师而言，是不易观测的；对学生而言，是不易操作的．

二是，教学过程随意，这一类型表现为没有遵循程序化的任务分析流程，缺少达成预期学习结果的学习条件，没有建立不同数学知识类型与教学方法之间的联系，教学方法的选择没有和学生的认知发展规律相结合．以“例1、例2、例3……”的形式呈现的是以“例题”为主线的教学设计，以“想一想”、“说一说”、“议一议”、“做一做”……的形式呈现的是以“活动”为主线的教学设计，将多个问题情境串成一个问题系列的是以“情境”为主线的教学设计．这只能说明近几年数学教学设计在形式上的多样性，并不意味着遵循了科学规范的教学步骤．以“圆的概念”为例，六年级将圆的定义概括为“到一个固定的点距离相等的所有点围成的图形”，九年级将圆定义为“到定点的距离等于定长的所有点的集合”，定义的变化反应出的是数学知识类型的变化，同时它们也应当遵循不同的学习规律．前者属于具体概念的学习，后者属于定义性概念的学习．相应地，前者应当将学生置于大量的事实例子中，形成圆的直观认识，从而概括出圆的本质特征（例规法）；后者则是在学生理解“定点”、“定长”、“集合”等下位概念的前提下，定义圆的概念，再结合具体的例子加以说明（规例法）．因此，如何根据不同数学知识类型的特点，设计合理的教学方式实现预期的教学目标，使学生达到最佳的学习效果，这是数学教学设计所要解决的问题[5]．

三是，教学评价盲目，表现为缺少有针对性和时效性的数学测评试题，缺乏自我反思的有效途径．如通过“指出在下列图形中的圆”（测评）来考查学生是否能“举例解释圆的特征”（目标）是不合适的．“指出”即辨认，能够胜任这一任务的学生达成的是概念性知识的记忆水平，这不足以说明学生已经达成高于记忆的理解水平，从而引发思考“车轮如何能滚动？井盖为什么是圆的？”等更能够测评出理解水平的试题．目标与测评在认知水平上是否一致是教学反思中的一项重要环节．

因此，目标的模糊性、过程的随意性、评价的盲目性是当前数学教学设计能力培养需要解决的关键问题．如何对数学知识内容和学生认知水平进行更为精准的定位；如何区分数学课程标准中提及的“结果目标”和“过程目标”；如何区分达成教学目标所需要的多个中间目标以及它们的上下位关系；如何确定学生的起点能力；如何为教学内容提供与之匹配的学习条件；如何设计遵循信息加工顺序的教学过程；如何根据不同的数学学习结果确定教学方法；如何确定学生已经达到既定的教学目标；如何对拟定的教学活动和评估试题进行调整等是对上述3个关键问题的进一步思考．

2 构建科学取向的数学教学设计能力培养体系的意义

国内外以研究教学规律为对象的理论，大致分为两大类：一类是依据哲学和经验总结所提出的理论，被称为哲学取向教学论；另一类是依据科学心理学，尤其是学习心理学和实证研究所提出的理论，被称为科学取向教学论[6]．“科学性”是高效教学行为的前提与归宿，是指数学教师在教心、导学与发挥数学的教育性方面更具有合理性[7]．因此，构建科学取向的数学教学设计能力培养体系是必要的，其重要意义主要体现在以下两方面．

2.1 指明了数学教学设计能力培养的方向

教学设计是运用系统方法分析教学问题和确定教学目标，建立解决教学问题的策略方案、试行解决方案、评价试行结果和对方案进行修改的过程[8]，是教师理论素养和学科素养的综合体现．数学教学设计能力培养既要考虑一般意义上对教学设计能力的要求，还要考虑到当前数学教学设计能力培养需要解决的关键问题．因此，数学教学设计能力的培养目标应当从能够设置精准的教学目标、设计科学规范的教学过程、组织及时有效的教学评价出发，自上而下地进行细化，最终形成数学教学设计能力培养体系（如图1所示）；而数学教学设计能力则应当以准确把握数学课程标准中的内容与目标为出发点，自下而上地进行培养．

图1 科学取向的数学教学设计能力培养体系（能力培养目标）

要想达成“准确地设置教学目标”、“科学规范地设计教学过程”需要诸多下位的培养目标作为前提条件．

在目标设置方面，首先要准确定位数学教材中静态的知识所属的类型，如表示“是什么”的基本事实与数学概念——“毕达哥拉斯定理就是我国的勾股定理”，“含有未知数的等式叫做方程”等；再如表示“怎么做”的程序性知识——“一元一次方程的求解分为5步：去分母、去括号、移项、合并同类项、系数化为1”等；其次要明确不同类型的数学知识在达成不同认知水平时（记忆、理解、运用、分析、评价、创造），将对应怎样的学习结果，如对“一元一次方程求解的5个步骤”进行记忆、理解时，所习得的学习结果属于数学基础知识，也就是认知心理学中的言语信息，而当这一程序性知识达到运用及以上水平时所对应的学习结果属于数学基本技能，也就是认知心理学中的智慧技能，这一程序性知识从较低的认知水平到较高认知水平的学习过程也是知识向技能转化的过程．最后，能够举例说明终点目标（学习结束时应达到的目标）、中间目标（学习过程中必须达到的目标）和起点能力（学习开始之前已经具备的数学基础知识、基本技能、基本思想方法、基本活动经验）之间的区别和联系，以“加权平均数”为例，要想达成“能用公式正确计算加权平均数，并利用计算结果来分析数据”这一终点目标，需要以“能够陈述出权的作用，并能够举例说明权的不同表达方式”、“能说出算术平均数和加权平均数的区别和联系”等中间目标为前提，归根究底要以“能够计算算术平均数”为达成上述中间目标的起点能力．

在过程组织方面，教师要分析不同数学学习结果所需的学习条件，这里的学习条件包括由学习者自身或数学知识本质决定的必要条件，如“全等三角形的性质和判定”是学习“相似三角形的性质和判定”的必要条件；还包括使学习更容易、更迅速、只起辅助作用的支持性条件，如学生在掌控圆规等数学工具时所需要的动作技能和数学学习过程中表现出的情感态度等；以及源于学习环境和教学者提供的外部条件，如图形计算器等技术工具以及教师配合概念学习给出的正反例证等．此外，教师还要根据数学学习结果的类型确定教学方法，如理解“哪一类数学学习结果一定要有正反例证，并加以强化和反馈”，“哪一类数学学习结果一定要结合样例学习，并设计变式练习”，等等．

2.2 建立数学教学设计中的三大联系

基于科学取向教学论的数学教学设计能力研究建立了数学学习结果类型与学习条件间的联系，数学学习结果类型与教学方法间的联系，以及教学目标、教学过程与教学评价的联系．

2.2.1 数学学习结果类型与学习条件间的联系

数学学习结果分为数学知识（即狭义的数学知识，对应认知心理学中的言语信息）、数学智慧技能、数学思想方法、数学问题解决和态度5种类型，每一类型下又分若干亚类，如数学知识包括符号表征学习、事实学习和数学关系的心理模型；数学智慧技能包括具体概念、定义性概念、规则和高级规则[9]．不同的数学学习结果需要不同学习条件的支持．如数学知识的学习以原有知识结构为基础，需要提供学习者辨别新旧知识的外部条件；数学具体概念的学习需要学生能够辨别认知结构中已有具体概念的例子，并在辨别的基础上总括出下位例子中蕴含的概念；数学定义性概念的学习以构成定义的相关具体概念为前提条件，或者学生的认知结构中具有同化下位概念的上位的一般概念或类似概念；数学规则的学习需要在概念的基础上学习；数学问题解决的学习是在简单规则基础上学习复杂规则；数学思想方法是在数学智慧技能达到相对自动化后形成的，并需要某些基本心理能力和认知发展水平的支持；数学情感态度的习得需要数学知识、数学智慧技能以及其它态度的支持[10]．

2.2.2 数学学习结果类型与教学方法间的联系

数学学习结果类型与学习条件建立联系的同时，也建立了与教学方法的联系．如对数学知识进行不断地强化，要把数学具体概念的学习暴露在充分的正反例证中；为数学定义性概念的学习提供揭示概念本质特征的例子；通过样例学习和变式练习来实现数学规则的迁移与运用，提供及时的反馈并在关键处给予指导；为数学问题解决提供突出图式的原型，将学生暴露在大量的图式例子当中并伴随及时的反馈；最终引导学生进行积极的归因以促进学生价值观的形成[11]．

2.2.3 教学目标与教学过程及教学评价的联系

修订后的布卢姆教育目标分类学能够有效地引领教师从知识类型和认知过程两个维度确定教学目标、设计教学过程，对提高教学品质与效率有重要的指导作用[12]．与此同时，教学目标的精准定位为教师的教学评价提供了有力的依据．这里的教学评价是指根据教学目标中的知识类型和认知水平制定的评价计划，并对评价结果做出解释[9]．高质量的教学需要伴随高质量的测评，否则高质量的教学也无助于提高学生的测评成绩[13]．因此，修订版分类学的重要成果之一就是将教学目标、教学活动以及教学评价置于同一个分类表中进行一致性的检验[14]．如表1所示，目标2、教学活动2和测评2三者出现在同一方格中，表示一致性程度高．目标1和测评1（目标3和活动3）二者出现在一个方格中，说明一致性程度较差，需要研究者重新审视这部分目标、活动和测评的设置．

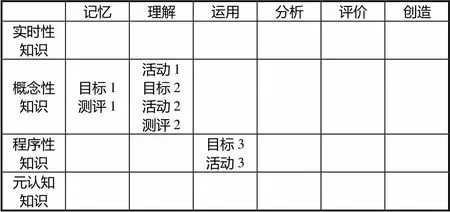
表1 “圆的认识”案例：目标与教学活动及测评的一致性问题

注：目标1=能够指出圆的各部分的名称．

目标2=能够用圆的知识来解释生活中的想象或用生活中的现象来解释圆的特征．

目标3=能使用工具画出圆．

活动1=折一折手中的圆形纸片，看看你都发现了什么？

活动2=给出长方形、正方形、平行四边形、梯形、三角形、长方体和圆柱体的图片，提问学生圆与他们相比，有什么不同的地方？

活动3=学生从扎钉、一根线、一个皮筋以及一根铅笔中选择材料制作画圆的工具．

测评1=指出圆的半径和直径．

测评2=生活中哪些地方离不开圆？

3 实施科学取向的数学教学设计能力培养的建议

3.1 明确科学取向教学论指导数学教学设计的意义

教师的教学设计观念根深蒂固，信念和知识影响着他们设定教学目标，处理教材，设计教学任务，实施教案[15]．认真分析一些优秀的教学设计后常能发现，这些教师往往潜在地运用任务分析等技术，只是没有得到理论层面的解释．当然，需要承认，不是所有优秀的教学设计都是在科学取向教学论的指导下完成的，但凡是优秀的教学设计都可以通过科学取向教学论进行解释并能经得起教育教学实践的检验．这些优秀的教学设计之所以没有达到技术层面，而仅仅停留在经验层面难以推广，就是因为缺乏基于教育学和心理学理论的诠释与概括．如上所论述的有关科学取向教学论对教学设计能力培养的重要意义，如果不能在相关培训中得以明确，而是直接进行教学设计技术上的指导，那么最终的培训效果无非是事倍功半．数学教学设计信念会指引教师开展教学设计，实施教学设计活动，教师拥有合理的数学教学设计信念是下一步进行教学实践的前提和保障[16]．因此，基于科学取向教学论培养数学教学设计能力的意义不仅在于对教师教学能力的提高，更是在寻求教师教学信念上的转变．

3.2 解决数学教师在提升教学设计能力的过程中遇到的困惑

随着现代认知心理学的发展，科学取向教学论取得了丰硕的成果，形成了更为科学、规范、具体的教学设计体系，为教师的教学设计提供了充分的心理学依据．与此同时，相对专业的话语体系对一线教师运用科学取向教学论指导自身教学设计带来困难．课题组在广州市花都区对一线数学教师进行了访谈，了解到教师对科学取向教学论存在的困惑主要包括：（1）知识类型与内容领域是什么关系？前者是根据信息加工学对信息编码方式的不同进行的划分，因此不同的知识类型对应不同的学习机制[11]，后者是按照知识表征的形式进行的划分，如中国义务教育阶段将数学学科划分为数与代数、空间与图形、统计与概率、实践与综合应用4大领域．事实上，并不是每一种教学方法都适用于所有的数学内容[17]．按照现代心理学的观点，如果不同的内容领域的知识具有相同的信息编码方式则对应相同的学习机制和相似的教学方法．（2）为什么要用“行为动词+名词”的形式描述教学目标？行为动词决定认知水平，名词决定知识类型，对知识类型和认知水平进行精准定位，可以形成可观察、可测量的教学目标，并能指导教学评价[14]．如将目标“进一步理解正数和负数的概念”改为“用生活中的实际问题解释（动词）正数和负数的意义（名词）”，则有助于教师了解学生应该达到的和已经达到的认知水平．（3）概念性知识与具体概念、定义性概念的区别是什么？概念性知识是修订版布卢姆教育目标分类学所提出的知识类型，如数学教材中表示“是什么”的知识；而具体概念、定义性概念属于智慧技能，是学习者在学习之后达成的学习结果．每一种学习结果都可以看作是教材中不同类型的知识在不同的认知水平上的表现．值得注意的是，教材中的概念性知识并不能在所有的认知水平上表现为数学智慧技能，如“=”、“”等概念在记忆、理解水平进行学习时所达成的学习结果只是一种数学符号语言．因此，适时、及时地解决好上述困惑对于数学教师运用科学取向教学论指导自身教学设计具有重要意义．

3.3 立足学科特点突出学科特色

依据数学课程标准的理念与要求，数学教师的专业素养应体现教师与数学学科的双重特性，需要与数学专业从业者和其它学科的教师有所区别，并同时体现出教师工作的实践取向[18]．数学教学设计能力作为数学教师的专业素养之一，需要构建有别于其它学科的数学学习结果分类系统，并给出具体的数学例子（如表2所示）．

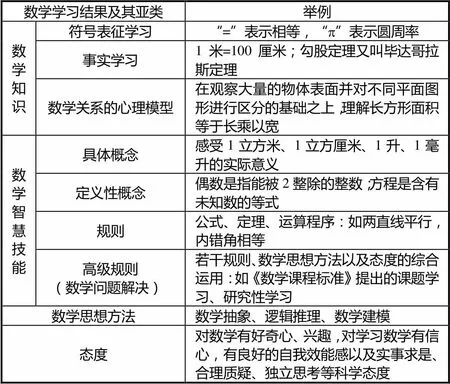
表2 数学学习结果及举例

学习“=”、“p”等符号的意义，都属于符号表征的学习；记住“1米=100厘米”，“勾股定理又叫毕达哥拉斯定理”等相对具体且不具有概括性的事件都属于事实学习；“在观察大量的物体表面并对不同平面图形进行区分的基础之上，理解长方形面积等于长乘以宽”，是客观事物在人脑中的表征，即数学关系的心理模型．符号表征学习、事实学习和数学关系的心理模型都属于数学知识的范畴[9]．

感受“1立方米”、“1立方厘米”等的实际意义，是运用一类事物的关键属性对事物进行分类的学习，属于数学具体概念；诸如“偶数是指能被2整除的整数”、“方程是含有未知数的等式”等以下定义的方式阐明概念的关键特征，属于数学定义性概念；数学学习过程中习得的公式、定理、运算程序等是学生运用若干概念之间的关系或程序对外办事的能力，即数学规则；若干数学规则的综合运用常伴随数学思想方法和态度的综合运用，如课题学习、研究性学习等都属于高级规则，相当于数学问题解决．数学具体概念与定义性概念、数学规则与高级规则都属于数学智慧技能的范畴[9]．

数学思想方法是指支配学习者如何学习、如何思考、如何问题解决的一套对内调控的能力．如分类思想、集合思想、归纳思想、演绎思想、函数思想、方程思想等都是数学思想方法．史宁中教授将抽象、推理和模型作为数学思想高度概括的结果，并称之为数学基本思想[19]．数学思想方法是数学基本思想下位的概念，具有一定的可操作性的，同时反映数学的某些思想，与一般意义上的具体方法不同[20]．态度是在数学学习过程中，对数学课程或数学知识技能本身形成的行为倾向，包括对数学有好奇心、兴趣、自信心，有良好的自我效能感以及实事求是、合理质疑、独立思考等科学态度[9]．

3.4 基于科学取向教学论实施数学教学设计能力评价

科学取向教学论为数学教学设计能力培养指明的方向也是为数学教师教学设计能力评价指明的方向．数学教学设计能力的评价从以下3个方面着手：一是要评价教师的目标设置和目标陈述，包括知识类型与认知过程的定位是否准确，目标是否具有可操作性和可观察性．二是要评价教师的教学过程，包括任务分析和教学步骤．对任务分析的评价包括能否将知识类型与认知水平准确地对应到数学学习结果；能否通过层级分析确定学生的中间目标和起点能力；能否分析习得数学学习结果所需要的学习条件；能否结合层级分析判断教学的重点和难点、选择需要的教具和学具等．对教学步骤的评价包括是否设置与教学目标相关的导入或情境，以达到“引起注意与告知目标”的目的；是否安排与起点能力相关的复习，以达到“提示学生回忆原有知识”的目的；是否遵循从起点能力到中间目标再到终点目标的层级顺序，以达到“呈现有组织的信息”的目的；是否建立起新旧知识的联系，将新知识建构在已有的认知图式中，以达到“阐明新旧知识关系，促进理解”的目的；是否针对关键属性设计变式练习，以促进数学知识认知结构的重组与改组，促进数学知识向数学智慧技能和思想方法的转化，以达到“对复习与记忆提供指导”的目的；是否提供提取数学知识的线索或应用数学智慧技能的新情境，以达到“知识的运用和迁移”的目的．三是对教师的教学评价进行评估，如所选择的数学试题是否与教学目标、教学活动在认知水平上是一致性的[11]．

科学取向的数学教学设计能力培养体系的建构为数学教师教学设计培训课程提供了依据．课题组从广州市花都区的调研中了解到，数学教师接受的培训内容主要围绕数学教学理论、数学方法论、数学教学设计研究、数学思想方法与教学研究、数学文化与数学课堂教学、数学教材教法、数学教学策略、数学教育技术以及中高考命题研究等．该调研结果与陈向明、王志明（2013）进行的“义务教育阶段教师培训调查：现状、问题与建议”中提到的：“较高比例的被调查者认为自己接受最多的培训内容前3位是教育教学理论、学科教学、教学方法及策略”的研究结论基本一致[21]．也就是说，大多数数学教师了解教材中的知识体系，清楚教材中例题习题的难易程度，理解教材的设计意图（章引言的作用、数学活动与本章内容的联系等），能够对学生进行学情分析，知道基本的教学方法（讲授法、发现法、探究法等），具备教学设计的基本教育经验．基于科学取向教学论的数学教学设计能力培养则是教师在基本教育经验的基础之上寻求更为行之有效的教学设计路径，如在教师研读教材的基础之上，明确数学学习结果的层级关系，引导教师组织教学内容；基于教师对学生的学情分析，指导教师设计符合学生认知发展规律的教学；根据教师对教法的了解，建立起数学学习结果与教学方法的联系等．

[1] 左坤．初中数学教师教学设计能力研究[J]．数学教育学报，2011，20（2）：41-44．

[2] 吴宝莹，陈敏．数学教学设计的取向与定位[J]．数学教育学报，2012，21（3）：89-90．

[3] 李孝诚，綦春霞，史晓锋．初中数学教师教学设计能力发展的实证研究——基于网络研修共同体教师专业发展的个案研究[J]．中国电化教育，2013，（3）：56-61．

[4] 沈威，卢建川，曹广福．美国纽约CCSSM背景下小学数学教学设计的特点与启示[J]．外国中小教育，2014，（10）：60-65．

[5] 王光生．知识类型与数学教学设计[J]．数学教育学报，2007，16（3）：27-31．

[6] 皮连生，吴红耘．两种取向的教学论与有效教学研究[J]．教育研究，2011，（5）：25-30．

[7] 王光明．高效数学教学行为的特征[J]．数学教育学报，2011，20（1）：35-38．

[8] 乌美娜．教学设计[M]．北京：高等教育出版社，1994．

[9] 张春莉，王小明．数学学习与教学设计（中学卷）[M]．上海：上海教育出版社，2004．

[10] 加涅．教学设计原理[M]．皮连生译．上海：华东师范大学出版社，1999．

[11] 皮连生．教育心理学（第四版）[M]．上海：上海教育出版社，2011．

[12] 李昌官．布卢姆认知目标新分类指导下的数学教学设计——以“数系的扩充和复数的概念”教学设计为例[J]．数学教育学报，2012，21（3）：67-71．

[13] 张春莉，马晓丹．布卢姆教育目标分类学修订版在数学学科中的应用[J]．课程·教材·教法，2017，（1）：119-124．

[14]  L·W·安德森．学习、教学和评估的分类学：布卢姆教育目标分类学修订版[M]．皮连生译．上海：华东师范大学出版社，2008．

[15]  Yang X.[M]. Conception and Characteristics of Expert Mathematics Teachers in China. Springer Fachmedien Wiesbaden, 2014.

[16] 冯振举，王惠扬子．职前数学教师教学设计信念转变的个案研究——以HPM视角下的勾股定理教学为例[J]．数学教育学报，2016，25（2）：59-65．

[17]  Soedjadi R.[C]. Proceedings of the Ninth International Congress on Mathematical Education. Springer Netherlands, 2004.

[18] 章勤琼，徐文彬．试论义务教育数学教师专业素养及其结构——基于教师专业标准与数学课程标准的思考[J]．数学教育学报，2016，25（4）：69-73．

[19] 史宁中．漫谈数学的基本思想[J]．数学教育学报，2011，20（4）：8．

[20] 马云鹏．关于数学核心素养的几个问题[J]．课程·教材·教法，2015，（9）：36-39．

[21] 陈向明，王志明．义务教育阶段教师培训调查：现状、问题与建议[J]．开放教育研究，2013，（4）：11-19．

Establishment of Cultivation System of Science-oriented Mathematics Instruction Design Competence

MA Xiao-dan, ZHANG Chun-li

(Faculty of Education in Beijing Normal University, Beijing 100875, China)

Establishing a cultivation system of science-oriented mathematics instruction design competence had important significance. It pointed out the direction of promotion and establishes three links in mathematics teaching-planning. Establishing a cultivation system of science-oriented mathematics instruction design competence included four suggestions: Firstly, we should make clear the value of science-oriented instructional theory to guide the design of mathematics teaching. Secondly, we should solve the problems which mathematics teachers encountered in the process of improving teaching design ability. Thirdly, we based on the characteristics of mathematics and highlight characteristics of the subject. Eventually, we implement evaluation of science-oriented mathematics instruction design competence.

science oriented teaching theory; mathematics teaching design; teaching goal; teaching process; teaching evaluation

[责任编校：周学智]

G420

A

1004–9894（2017）04–0056–05

2017–04–01

北京市教育科学“十二五”规划重点课题——专家教师原型观下课堂教学执行力的提升（AIA15226）

马晓丹（1989—），女，天津人，博士生，主要从事数学教育研究．