考虑处理机下线时间的可分任务调度优化模型

王晓丽，王宇平，蔡 坤，赖俊凡



考虑处理机下线时间的可分任务调度优化模型

王晓丽，王宇平，蔡 坤，赖俊凡

(西安电子科技大学计算机学院 西安 710071)

随着科学应用逐渐趋于数据密集型计算，为并行与分布式系统寻求高效的任务调度策略成了研究的热点问题。已有的可分任务调度模型均假设所有处理机都能100%的完成子任务的计算，即处理机在完成任务计算之前一直保持在线状态。实际上，并行与分布式系统中不同处理机的在线时间可能不同。若忽略处理机的在线时间，为其分配的任务量过大，则任务的完成时间可能超出处理机的下线时间，从而造成任务的计算无法按时完成。因此，为处理机分配任务时应充分考虑处理机下线时间的限制。为解决上述问题，该文提出了一种新的考虑处理机下线时间的可分任务调度优化模型，并设计了全局优化遗传算法求解该模型。最后，通过仿真实验结果验证了模型和算法的有效性。

可分任务调度; 遗传算法; 下线时间; 并行与分布式系统

随着大数据时代的来临，数据的规模呈爆炸式增长，如何高效快速处理并分析数据成了研究的重点和难点问题。大数据应用问题，如大规模矩阵运算、DNA测序分析、卫星图像处理等，虽然数据规模庞大，但是大都可以抽象为可分任务，即任务可以被划分为任意大小的子任务，子任务间相互独立且没有优先级关系[1]。并行与分布式系统下可分任务调度问题的目标是寻求最优的任务分配方案使得任务的完成时间最短。

针对并行与分布式系统下常见的线型拓扑结构、总线型拓扑结构和树型拓扑结构，已有很多文献对可分任务的最优调度策略进行了研究。文献[2]给出了同构线型网络下最优任务分配方案的紧式耦合解，文献[3]给出了同构树型网络与总线型网络下任务分配方案的渐近解。文献[4]给出了异构星型网络下任务分配方案的紧式耦合解，并且证明了处理机调度顺序在遵循通信速率递减的情况下任务的完成时间最短。对于异构树型网络，文献[5]的研究表明处理机的调度顺序只依赖于其通信速率而非计算速率。然而，这些研究成果都没有考虑处理机的计算启动开销和网络的通信启动开销。文献[6-7]在调度模型中引入了启动开销，分析了总线型网络下启动开销和处理机的调度顺序对任务完成时间的影响，证明了当处理机遵循计算速率递减的顺序时任务的完成时间最短。为了使可分任务调度模型更符合分布式平台的实际网络环境，文献[8]将可分任务调度模型扩展到多源网格环境中，文献[9]研究了云平台下处理机带宽受限的可分任务调度问题，文献[10]将其扩展到混合云计算平台环境中，文献[11-12]将其扩展到无线传感器网络中，文献[13-14]将其扩展到实时环境中。

但是，已有的可分任务调度模型均假设所有处理机都能100%的完成所分配的子任务，即处理机在完成所分配的子任务之前一直保持在线状态[15]。然而在实际的网络环境下这个假设并不成立，不同处理机的下线时间可能不同。若为处理机分配的任务量过大，则任务的完成时间可能超出处理机的下线时间，从而造成任务的计算无法按时完成。若处理机未完成计算就已下线，则为其分配的任务需要等待其他处理机完成计算空闲后，调度到其他仍在线的处理机上重新开始计算，从而导致任务的总完成时间增大。鉴于此，本文提出了一种新的考虑处理机下线时间的可分任务调度优化模型，并且设计了新的遗传算法对模型进行求解。

1 考虑处理机下线时间的可分任务调度优化模型

1.1 问题描述

(1)

1.2 可分任务调度优化模型

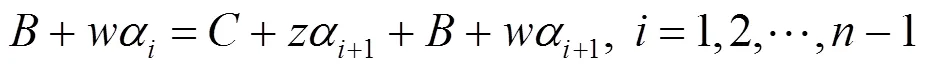
(3)

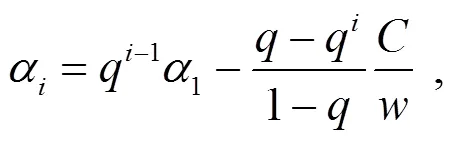
将式(4)带入式(1)可得：

(5)

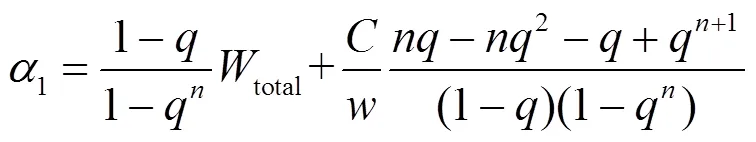
(8)

与情况1不同的是，对于情况2，无法直接通过计算得到所有处理机的最优任务分配方案，也就无法直接得到总任务的完成时间。这主要是因为可能只有部分处理机受下线时间的约束，因此无法通过式(7)得到所有处理机的最优任务分配方案。鉴于此，本文建立了以下考虑处理机下线时间的可分任务调度优化模型：

模型的目标是总任务的完成时间最短，变量是参与计算的最优处理机数目和处理机的最优任务分配方案。模型的约束条件1)表示并非所有的处理机都必须参与计算；约束条件2)表示每个处理机所分配的任务量必须非负，且不能超过总任务量；约束条件3)表示所有处理机分配的任务量之和为总任务量；约束条件4)表示所有处理机完成所分配任务的时间必须小于等于其下线时间。

2 全局优化遗传算法

为了求解建立的优化模型，本文设计了新的全局优化遗传算法，包括编码与解码规则、交叉与变异算子、修正算子和局部搜索算子。

2.1 编码与解码

2.2 交叉和变异算子

交叉算子采用三三交叉的方式，即3个父代两两交叉生成3个子代。具体操作步骤如下：首先，按照交叉概率从交叉池中选择3个个体作为父代，然后随机生成3个整数、和满足，按照图3所示的方法进行交叉，使得每个子代个体都包含3个父代个体的部分基因。通过三三交叉可以更大程度地增加种群的多样性，较常用的两两交叉而言，可以加快算法收敛于全局最优解，从而提高整个算法的执行效率。

图3 交叉示意图

2.3 修正算子

如前文所述，不论是种群的初始化，还是交叉及变异产生的新个体，都不能保证个体满足模型的全部约束条件，因此需要对个体进行修正。修正算子的主要思想如下：若处理机完成所分配的任务量的时间超出了其下线时间，则将超出下线时间的部分(又称为冲突部分)调整到相邻的下一台处理机上执行。若第一轮调整过后，处理机的完成时间也超出了其下线时间，则继续将的冲突部分调整到相邻的下一台处理机上执行，循环此过程，直至冲突完全消除。可见，修正的过程是一个迭代的过程。

图4给出了一种不满足模型约束的可分任务调度时序图。从该图可以看出，处理机完成任务所需要的时间超出了该处理机的下线时间，图中灰色部分即为冲突部分。因此，需要对处理机的任务量进行调整。首先，将冲突部分对应的任务量分配给处理机，图5给出了调整后的可分任务调度时序图。选择分配给相邻的下一台处理机是考虑到每台处理机的开始时间与其前面的所有处理机的任务分配量直接相关。如果将冲突部分调整到前面的处理机，调整后将推迟后续所有处理机的开始时间，导致新的冲突产生。从图5可以看出，将处理机的冲突部分调整给处理机后，处理机产生了新的冲突部分，因此需要继续迭代修正过程，直至冲突全部消除。

2.4 局部搜索算子

为了增强算法的局部搜索能力，提高算法的收敛速度，本文为遗传算法引入了局部搜索算子。

算子的设计思想如下：由于所有处理机是同构的，因此若不考虑处理机的下线时间，为达到总任务的完成时间最短，调度顺序靠前的处理机其分配的任务量应大于调度顺序靠后的处理机。鉴于此，可以通过置换相邻两台处理机的任务分配量来寻求更优的个体。局部搜索算子的具体执行过程如下：对所有处理机的任务量从后向前逐个进行比较，如相邻两个处理机中，前面处理机的任务完成时间小于其下线时间且后面处理机所分配的任务量大于前面处理机的任务量，那么将两个处理机的任务量进行交换。图6给出了一种可能的局部搜索执行过程。

2.5 可分任务调度遗传算法整体框架

基于前文设计的编码与解码规则、交叉与变异算子、修正算子和局部搜索算子，下面给出考虑处理机下线时间的可分任务调度遗传算法整体框架。

算法1 考虑处理机下线时间的可分任务调度遗传算法。

7) (终止条件)若算法达到终止条件，则终止；否则，转至2)。

3 实验与结果分析

为了验证本文提出的算法的有效性，将其与已有算法[15]进行了多组对比实验，其中并行与分布式系统的参数设置如下：，，，，；遗传算法的参数设置如下：种群大小，交叉概率，变异概率，精英保留个数，终止条件为进化代数。

实验1 固定处理机的下线时间，对比两个算法在不同任务量情况下求得的任务完成时间。20台处理机的下线时间分别为：

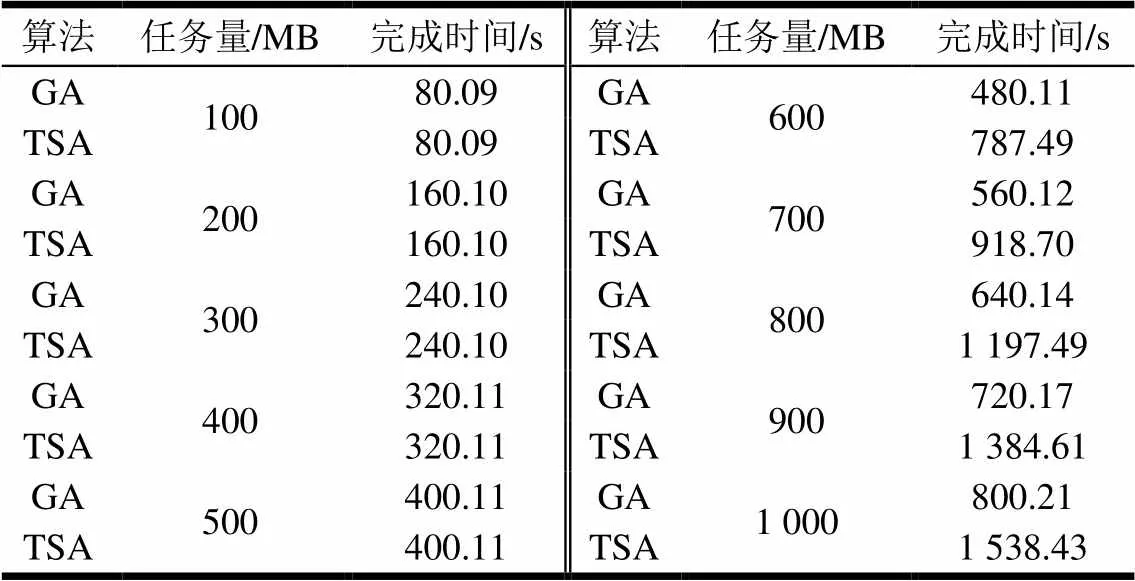
表1 不同任务量情况下两种算法对比的实验结果

为了更直观地反应表1中两种算法的对比结果，图7给出了两种算法的任务完成时间随任务大小的变化趋势。由图7可以看出，随着任务量的增大，两个算法求得的任务完成时间的差距越来越大。这主要是因为本文的算法在任务调度前充分考虑到各个处理机下线时间的限制，为下线时间较早的处理机分配合理的任务量，避免了任务的重新分配和重新计算，从而减少了总任务的完成时间。随着任务量的增大，处理机下线时间的影响越来越明显，因此两个算法求得的任务完成时间的差距就越来越大。

实验2 固定任务量，对比两个算法在不同下线时间情况下求得的任务完成时间。任务量，处理机～的下线时间～是指数分布的随机数。图8和图9分别给出了算法GA和TSA的任务完成时间随处理机下线时间的平均值(300～1 200)的变化趋势。

由图8和图9可以看出，随着处理机下线时间平均值的增大，两个算法求得的任务完成时间趋于平稳，结果趋于一致。这主要是因为针对固定大小的任务，随着下线时间的增大，处理机不再受下线时间的影响，当所有处理机同时完成计算时任务的完成时间最短，因此两个算法求得的任务完成时间相同。当下线时间的平均值较小时，部分处理机开始受到下线时间的影响，两个算法求得的任务完成时间不同且GA求得的任务完成时间要远小于对比算法TSA求得的任务完成时间。而且，针对固定大小的任务，处理机下线时间的平均值越小，对任务完成时间的影响越大，本文提出的算法GA相较于TSA的优势就越明显。

4 结束语

本文在考虑实际并行与分布式环境中处理机存在下线时间的基础上，分析了两种不同时间约束下的任务调度过程，提出了一种新的考虑处理机下线时间的可分任务优化调度模型，并设计了高效的全局优化遗传算法对其进行求解。实验结果表明本文提出的算法能够针对不同处理机的下线时间有针对性的为其分配任务，使得总任务的完成时间最短。

[1] BHARDWAJ V, GHOSE D, MANI V, et al. Scheduling divisible loads in parallel and distributed systems[M]. Los Alamitos CA: IEEE Computer Society Press, 1996.

[2] MANI V, GHOSE D. Distributed computation in linear networks: Closed-form solutions[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(2): 471-483.

[3] GHOSE D, MANI V. Distributed computation with communication delays: Asymptotic performance analysis[J]. Journal of Parallel and Distributed Computing, 1994, 23(3): 293-305.

[4] BHARADWAJ V, GHOSE D, MANI V. Optimal sequencing and arrangement in distributed single-level tree networks with communication delays[J]. IEEE Transactions on Parallel and Distributed Systems, 1994, 5(9): 968-976.

[5] KIM H J, JEE G I, LEE J G. Optimal load distribution for tree network processors[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(2): 607-612.

[6] SURESH S, MANI V, OMKAR S N. The effect of start-up delays in scheduling divisible loads on bus networks: an alternate approach[J]. Computers & Mathematics with Applications, 2003, 46(10): 1545-1557.

[7] VEERAVALLI B, LI X, KO C C. On the influence of start-up costs in scheduling divisible loads on bus networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2000, 11(12): 1288-1305.

[8] MURUGESAN G, CHELLAPPAN C. Multi-source task scheduling in grid computing environment using linear programming[J]. International Journal of Computational Science and Engineering, 2014, 9(1): 80-85.

[9] LIN W, LIANG C, WANG J Z, et al. Bandwidth‐aware divisible task scheduling for cloud computing[J]. Software: Practice and Experience, 2014, 44(2): 163-174.

[10] HOSEINYFARAHABADY M R, LEE Y C, ZOMAYA A Y. Randomized approximation scheme for resource allocation in hybrid-cloud environment[J]. The Journal of Supercomputing, 2014, 69(2): 576-592.

[11] SHI H, WANG W, KWOK N M, et al. Adaptive indexed divisible load theory for wireless sensor network workload allocation[J]. International Journal of Distributed Sensor Networks, 2013(1): 1-18.

[12] DAI L, SHEN Z, CHEN T, et al. Analysis and modeling of task scheduling in wireless sensor network based on divisible load theory[J]. International Journal of Communication Systems, 2014, 27(5): 721-731.

[13] HU M, VEERAVALLI B. Dynamic scheduling of hybrid real-time tasks on clusters[J]. IEEE Transactions on Computers, 2014, 63(12): 2988-2997.

[14] HU M, VEERAVALLI B. Requirement-aware strategies for scheduling real-time divisible loads on clusters[J]. Journal of Parallel and Distributed Computing, 2013, 73(8): 1083-1091.

[15] ROSAS C, SIKORA A, JORBA J, et al. Improving performance on data-intensive applications using a load balancing methodology based on divisible load theory[J]. International Journal of Parallel Programming, 2013, 42(1): 94-118.

编 辑 漆 蓉

Off-Line Time Aware Divisible-Load Scheduling Optimization Model

WANG Xiao-li, WANG Yu-ping, CAI Kun, and LAI Jun-fan

(School of Computer Science and Technology, Xidian University Xi’an 710071)

As scientific applications become more data intensive, finding an efficient scheduling strategy for massive computing in parallel and distributed systems has drawn increasingly attention. Most existing scheduling models assume that all processors can 100% finish computing, that is, they keep online during the completion of assigned workload fractions. In fact, in the real parallel and distributed environments, different processors have different off-line time. Therefore, off-line time constraints of processors should be taken into account before distributing of the workload fractions; otherwise, some processors may not be able to fish computing their assignments. To solve the above issue, this paper proposes an off-line time aware divisible-load scheduling model and designs an effective global optimization genetic algorithm to solve it. Finally, experimental results illustrate the effectiveness of the proposed model and the efficiency of the proposed algorithm.

divisible-load scheduling; genetic algorithm; off-line time; parallel and distributed systems

TP393

A

10.3969/j.issn.1001-0548.2017.01.014

2015-07-13；

2016-05-31

国家自然科学基金(61402350, 61472297, 61572391)；中央高校基本科研业务费专项资金(JB150307)

王晓丽(1987-)，女，博士，主要从事并行与分布式系统下的任务调度方面的研究.