基于多阶段多向核熵成分分析的间歇过程故障检测方法

邓晓刚，张琛琛，王磊



基于多阶段多向核熵成分分析的间歇过程故障检测方法

邓晓刚，张琛琛，王磊

（中国石油大学（华东）信息与控制工程学院，山东青岛266580）

针对间歇过程的非线性、多阶段特性，提出一种基于多阶段多向核熵成分分析(multistage-MKECA, MsMKECA)的故障检测方法。针对间歇过程的多阶段特性，建立一种时序核熵主元关联度的矩阵相似性阶段划分方法，实现对间歇生产过程的多阶段划分；针对传统批次展开方式在线监控需要预估批次未来值的缺陷，进一步引入一种批次-变量三维数据展开方式建立每个阶段的MKECA非线性统计模型，实现对间歇过程的分阶段监控。最后对盘尼西林发酵过程开展仿真研究，结果表明所提方法能够比传统MKECA方法更为快速地进行故障检测。

故障检测；MKECA；间歇过程；多阶段

引 言

现代工业生产中，间歇过程在精细化工、生物制药及金属加工等高附加值产品领域的应用正愈加广泛，已成为现代制造业的一种重要生产方式[1]。因此，对间歇生产过程进行实时监控，及时发现过程故障促使生产人员做出调整，最大限度地降低经济损失及避免人员伤亡，具有重要的经济意义和社会价值[2]。

在目前的间歇过程安全监控技术研究中，基于数据的多元统计方法是一类重要的故障检测方法。典型的间歇过程故障检测方法有多向主元分析(MPCA)方法[3]和多向独立元分析(MICA)方法[4]，但是该方法只是一种线性化的方法，并没有考虑到过程变量间的非线性。为了更好地挖掘过程数据间的非线性关系，文献[5-6]运用核方法将数据映射到高维空间中，分别提出了多向核主元分析(MKPCA)方法和多向核独立元分析(MKICA)方法。文献[7]结合MPCA方法，将间歇过程进行多阶段划分，并在划分的各个阶段分别进行过程监控。文献[8]提出一种多动态核聚类的核主元分析(DKCPCA)方法，提高了对多阶段间歇过程弱故障的检测能力。文献[9]针对间歇过程存在的非线性高斯和非高斯特性，进一步提出了一种KICA-PCA两步过程监控方法。

核熵成分分析[10](kernel entropy component analysis, KECA)方法作为近年来提出的一种新的非线性特征提取方法，从Renyi熵变化的角度提取代表过程特征的数据信息，已被初步引入化工过程故障监控领域[11-14]。文献[15]将KECA方法引入间歇过程故障监控领域，提出了多向核熵成分分析(MKECA)方法，并分析了MKECA方法相比于传统MKPCA方法的优势。该方法虽然能很好地挖掘过程的非线性特性，但是忽略了对间歇过程的多阶段特性分析[16-17]。

针对MKECA方法未考虑间歇过程的多阶段特性问题，本文提出一种基于多阶段多向核熵成分分析（MsMKECA）的间歇过程故障检测方法。该方法首先构建一种新的核熵主元关联度的矩阵相似性衡量指标，并考虑过程运行的时序性实现对过程的阶段划分，进一步在划分的各个阶段引入一种批次-变量三维数据展开方式建立多阶段MKECA故障检测模型。最后本文对盘尼西林发酵过程开展仿真实验研究，验证所提方法的有效性。

1 核熵成分分析（KECA）方法

核熵成分分析(KECA)[10,18]方法由Jenssen从Renyi熵的角度提出的，Renyi熵是一种对数据信息定量描述的信息熵，其定义为

其中，()代表Renyi熵，()为样本的概率密度，()可通过Parzen密度估计获得，估计形式如

(2)

其中，代表样本数据={1,…,}中的第个样本，为样本数，ker(,)代表Mercer核函数。

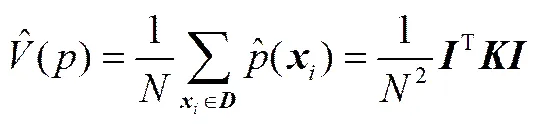
其中，为×维核矩阵，其第(，)个元素为ker(,)，为元素均为1的×1维向量。由于核函数ker(,)代表了非线性函数()和()的内积运算，故可将式(3)表示为

(4)

根据式(1)和式(3)，()可通过核矩阵求取，进而对核矩阵进行特征值分解，如

=ET(5)

其中，={1,…,}为特征向量矩阵，=diag(1,…, l)为特征值对角阵。根据式(3)和式(5)进一步可得

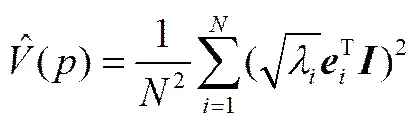
可以看出，式(6)中每一特征值及对应特征向量对Renyi熵产生不同程度的贡献，贡献度的不同可以作为排列特征值和特征向量的一个标志。KECA可通过熵值贡献率选择对Renyi熵值贡献最大的前个特征值及对应特征向量。

对每一非线性映射样本()可计算其在特征向量的核熵投影t

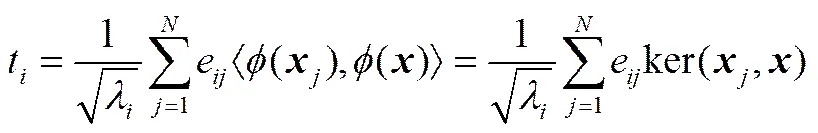
通常认为前个投影向量涵盖了样本数据的主要信息，其投影后的主元空间可表示为KEC=[12…t]。

KECA方法监控统计量的计算通常针对主元空间和残差空间分别建立2统计量与SPE统计量[11,15]，分别如式（8）和式（9）所示。

2=[1,2,…,t]-1[1,2,…,t]T(8)

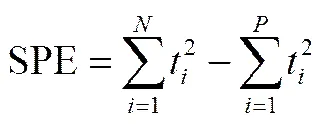
其中，t代表非线性样本在特征向量的核熵投影，-1为保留的个特征值的逆矩阵。

KECA方法监控控制限的获得可选用一种不需要统计量分布的非参数估计方法，即核密度估计[19]来求得，如

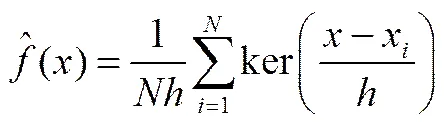
其中，为输入样本，为样本总数，为窗宽，ker(•)为核密度估计函数。本文进一步选取Gaussian核函数作为核密度估计函数，如

(11)

窗宽参数的计算参照Sliverman[20]提出的拇指法则，如

其中，为所选输入样本的标准差。

2 基于时序核熵主元关联度的多阶段建模

本节提出一种基于MsMKECA的间歇过程故障检测方法。该方法从两方面对MKECA方法进行改进，一方面建立一种时序核熵主元关联度的阶段划分方法，对过程进行多阶段划分；另一方面在划分的各个阶段引入一种批次-变量三维数据展开方式建立MKECA故障检测模型，更为快速地对过程故障进行检测。

2.1 核熵主元关联度的矩阵相似性指标

对于具有相同行列大小的两矩阵和，以数据集为例，对其进行非线性变换(·)，变换后的核矩阵是=()T()，通过对核矩阵进行特征值分解，确定特征值矩阵a及特征向量矩阵，由Renyi熵值大小排列特征值和特征向量，并确定其前个投影向量，求得核熵主元空间。同理，对另一相同行列大小的矩阵，获取核熵主元空间，定义两矩阵的核熵主元关联度[21]为

其中，CE代表核熵主元关联度，和分别代表按照Renyi熵值大小排列确定的和特征值平方根的对角阵。

结合核函数定义，考虑所选矩阵核熵主元对应的Renyi熵值权重对阶段划分的影响，提出一种新的核熵主元关联度ICE为

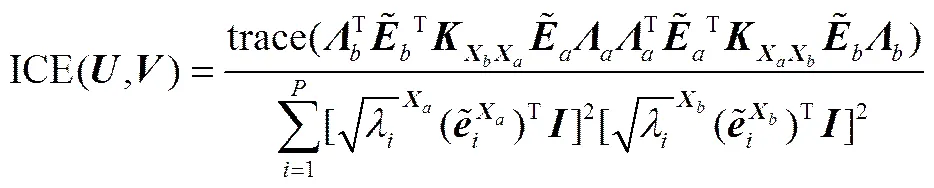
其中，K=()T()，K=()T()，为元素均为1的向量，和分别为数据集非线性变换后按照Renyi熵值大小排列选取的特征值平方根和特征向量，同理和分别为数据集非线性变换后按照Renyi熵值大小排列选取的特征值平方根和特征向量。

根据ICE可以有效衡量两矩阵间的相对变化。

2.2 核熵主元关联度的时序阶段划分

引入ICE矩阵相似性指标后，进一步考虑间歇过程运行的时序性，将滑动窗技术[22-23]引入相似性指标计算之中，实现对过程的多阶段划分。

首先对采集到的三维间歇过程批次数据(××)，其中为批次数，为变量个数，为采样点个数，按批次方向展开成二维数据矩阵(×)，对各过程变量进行标准化处理后，沿时间轴方向将其切割成个时间片矩阵(×)，=1,2,…,。由于每个时间片矩阵具有相同的维数，从而确定窗口为两时间片矩阵大小的滑动窗，并将其沿时间方向序列依次移动，依次计算该滑动窗口内相邻两时间片矩阵的核熵主元关联度ICE，得到时序核熵主元关联度TICE()

TICE() =ICE(,+1) (15)

其中，=1,2,3,…,-1。TICE的大小衡量了时间方向上滑动窗口内相邻两矩阵的核熵主元的相对变化，处在同一稳定阶段的时序滑动窗口内相邻时间片矩阵有相近大小的核熵主元关联度，当连续几个滑动窗口内矩阵核熵主元关联度发生较大变化时，表明生产过程正发生相应改变。

由于稳定阶段和变化过程其时间方向上连续样本点的TICE值会有不同变化，结合一种离群因子检测方法——局部离群因子(LOF)[24-25]，实现对过程的时序阶段划分。当连续几个样本点处于同一平稳过程时，样本点的局部可达密度与其邻居的局部可达密度相近，即属于同一状态的样本点的LOF值接近于1。本文进一步将沿时间方向上连续3个TICE样本点的局部离群因子均大于1.5的连续离群变化过程看作过渡过程，最终实现对间歇过程的时序阶段划分。

2.3 批次-变量展开方式

采用时序核熵主元关联度方法对间歇过程进行多阶段划分后，需要对各阶段数据矩阵展开为二维数据矩阵，才能建立过程故障检测模型。

传统的三维数据矩阵展开是基于批次的展开方式，它将三维批次数据(××)展开为二维矩阵(×)，如

其中，,k代表第个批次在第个时刻的变量x。对式(16)按列进行标准化处理，使得该矩阵每列均值为0，方差为1，然而该展开方式具有在线监控需要预估批次未来值的缺陷。

针对以上问题，本文引入一种批次-变量三维数据展开方式[26]构建MsMKECA模型，无须预估批次未来数据，能够更为有效地监控过程变化。

首先将采集到的三维批次数据(××)按批次方向展开为如式(16)所示的二维矩阵(×)，对其按列进行标准化处理后，进一步按变量方向展开，构成二维矩阵(×)，如

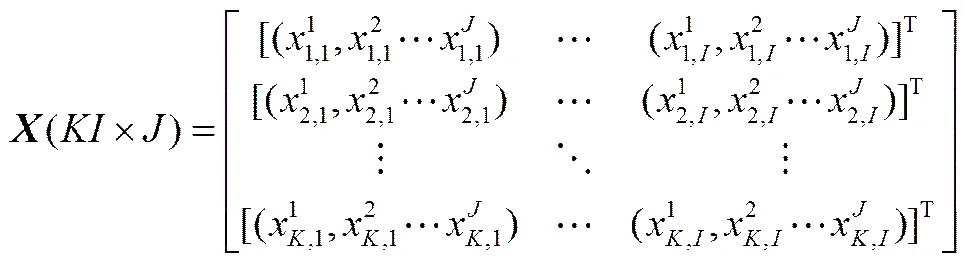
其中，,i代表第个批次在第个时刻的变量x。结合式(16)和式(17)，应用KECA分析即可建立MsMKECA模型。

2.4 MsMKECA故障检测方法

MsMKECA方法分为离线建模与在线监控两个阶段，分别如下。

2.4.1 离线建模阶段

（1）将正常间歇过程三维数据(××)按批次方向展开成二维数据(×)，并对每一过程变量在每个采样时刻下的不同操作批次做均值和方差标准化处理。

（2）获得标准化后的各时间片矩阵(×)分别将其映射到核特征空间，并按照本文所提时序核熵主元关联度阶段划分方法，实现过程的多阶段划分。

（3）在划分的每一阶段内引入批次-变量展开方式建立多阶段MKECA故障检测模型，求取各阶段样本的2和SPE监控统计量，由核密度估计各阶段统计量样本95%分布值获得控制限。

2.4.2 在线监控阶段

（1）获取新的采样过程数据按批次方向展开并用离线建模时的均值与方差进行标准化处理，进一步按变量方向进行展开。

（2）根据采样点时刻判断其属于哪个阶段，计算该时刻的核特征矩阵。

（3）计算该采样点时刻的2和SPE统计量，判断统计量是否超限确定是否发生故障。

3 仿真实验研究

盘尼西林发酵过程是一个典型的非线性、多阶段的间歇生产过程。本文采用了Cinar课题组提出的盘尼西林仿真平台Pensim2.0，该平台基于Birol等提出的盘尼西林生产过程的Benchmark模型，已是研究间歇过程故障检测的一个标准平台[27-28]。盘尼西林发酵过程如图1所示。

本仿真实验监控变量包括底物流加速率、底物流加温度、发酵产生热量、二氧化碳浓度、溶解氧浓度、冷却水流量、搅拌功率、发酵温度、空气流量、pH[22,29]共10个变量，共仿真产生30个正常批次，进行离线建模。本文产生每一正常批次的初始条件均在一定范围稍加改变，且过程变量均加入了一定大小高斯测量噪声，以更好地模拟实际工业生产状况。设置仿真实验中每一批次反应时间为400 h，采样时间为2 h，共产生200个采样点。

常用核函数有高斯核函数(x,y)= exp(-||x-y||/2)，多项式核函数(x,y)= (1+<x,y>)等，但如何选取最佳核函数并没有一个较为明确的准则，结合文献[21，30]，本文在求取时序核熵主元关联度和建立MsMKECA故障检测模型时均选用二项式核函数(x,y)=(1+<x,y>)2。

图2显示了时序核熵主元关联度的阶段划分结果。

采用所提方法对过程数据可以分为3个明显的阶段，分别为1～50 h，51～82 h，83～400 h。该阶段划分结果并不一定与盘尼西林发酵过程真正的物理阶段相吻合，更侧重于局部模型对过程数据的解释能力。

本仿真实验通过Renyi熵值贡献度选取大于95%的核特征值和特征向量构建核熵投影主元空间，并且监控控制限通过正常建模样本2和SPE统计量的95%样本分布值来求取。

为验证所提MsMKECA方法的有效性，图3显示了该方法对正常建模批次样本的监控效果，其2统计量与SPE统计量几乎均在控制限之内，可知该样本批次是正常的。

为检验所提方法对故障批次样本的检测能力，本文通过盘尼西林仿真平台产生了两个故障批次样本，表1列出了仿真实验用到的故障类型。

表1 故障类型

本文定义故障检出采样点与故障报警率两个指标[31]，以衡量所提方法对过程故障的检测效果。将故障检出采样点定义为连续5个采样点超出控制限的采样点，并将故障发生到结束的该段时间内，统计量超出控制限的采样点个数与故障采样点总个数的比值定义为故障报警率。

图4列出了MKECA方法对故障批次F1的2和SPE统计量的监控图，图5为阶段划分后传统批次展开方式的MKECA(improved MKECA，IMKECA)方法的2和SPE统计量监控图，图6列出了所提MsMKECA方法的2和SPE统计量监控图。

对于故障批次F1，MKECA方法的2和SPE统计量分别在第87和82个采样点检测到故障的发生，IMKECA方法的2和SPE统计量分别在第85和74个采样点检出故障，说明IMKECA方法相比于MKECA方法，能够更为快速地对过程故障进行检测。MsMKECA方法与IMKECA方法相比，其2和SPE统计量分别在第78和70个采样点检测到故障发生，故障检出采样点进一步提前。

图7～图9分别显示了3种方法对故障批次F2的检测效果，IMKECA方法相比于MKECA方法，其2和SPE统计量的故障检出采样点分别提前了1个和13个采样点，可以看出多阶段模型使得监控过程更加精确，故障检出采样点进一步提前。MsMKECA方法的2和SPE统计量分别在第110和80个采样点检出故障，比IMKECA方法分别提前了24个和9个采样点，进一步提高了故障报警率。

表2和表3分别列出了3种方法对所列故障批次仿真检测的故障检出采样点与故障报警率。

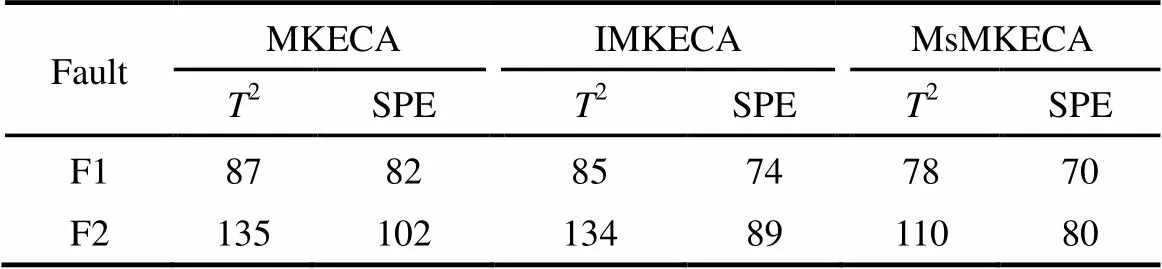
表2 3种方法的故障检出采样点对比

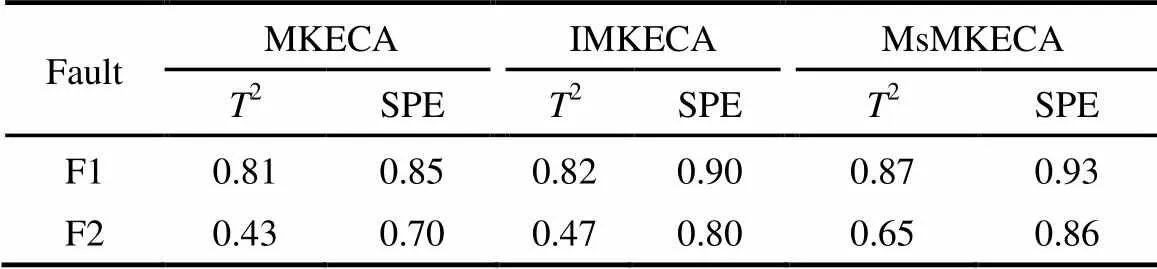
表3 3种方法的故障报警率对比

从故障批次的故障检出采样点和报警率的对比可知，所列方法对过程故障的检测都是有效的。IMKECA方法相比于MKECA方法，故障检出采样点更为提前，显示了多阶段建模监控的优势。本文提出的MsMKECA方法，在考虑多阶段建模的同时，引入批次-变量三维数据展开方式，克服了传统批次展开方式在线监控需要预估批次未来值的缺陷，与IMKECA方法相比，能够更为快速地对过程故障进行检测。

4 结 论

针对非线性与多阶段等特点的间歇过程，提出了一种基于MsMKECA的故障检测方法。该方法通过构建时序核熵主元关联度矩阵相似性指标，实现对间歇过程的阶段划分；并进一步引入批次-变量三维数据展开方式，在划分的各个阶段进行过程监控。最后通过对盘尼西林发酵平台的仿真实验研究表明，所提方法能够更为及时地检测过程故障，具有更高的故障报警率。

References

[1] 陆宁云, 王福利, 高福荣,等. 间歇过程的统计建模与在线监测[J]. 自动化学报, 2006, 32(3): 400-410. LU N Y, WANG F L, GAO F R,. Statistical modeling and online monitoring for batch processes[J]. Acta Automatica Sinica, 2006, 32(3): 400-410.

[2] 赵春晖, 陆宁云. 间歇过程统计监测与质量分析[M]. 北京: 科学出版社, 2014. ZHAO C H, LU N Y. Batch Process Statistical Monitoring and Quality Analysis[M]. Beijing: Science Press, 2014.

[3] NOMIKOS P, MACGREGOR J F. Monitoring batch processes using multiway principal component analysis[J]. AIChE Journal, 1994, 40(8): 1361-1375.

[4] CHANG K Y, LEE D S, VANROLLEGHEM P A. Application of multiway ICA for on-line process monitoring of a sequencing batch reactor[J]. Water Research, 2004, 38(7): 1715-1732.

[5] LEE J M, YOO C K, LEE I B. Fault detection of batch processes using multiway kernel principal component analysis[J]. Computers & Chemical Engineering, 2004, 28(9): 1837-1847.

[6] LEE J M, QIN S J, LEE I B. Fault detection of nonlinear processes using kernel independent component analysis[J]. Canadian Journal of Chemical Engineering, 2007, 5(4): 526-536.

[7] LU N Y, GAO F R, WANG F L. Sub-PCA modeling and on-line monitoring strategy for batch process[J]. AIChE Journal, 2004, 50(1): 255-259.

[8] 王亚君, 孙福明. 基于多动态核聚类的间歇过程在线监控[J]. 化工学报, 2014, 65(12): 4905-4913. WANG Y J, SUN F M. Multiple dynamic kernel clustering based online monitoring for batch process[J]. CIESC Journal, 2014, 65(12): 4905-4913.

[9] ZHAO C, GAO F, WANG F L. Nonlinear batch process monitoring using phase-based kernel independent component analysis-principal component analysis[J]. Industrial & Engineering Chemistry Research, 2009, 48(20): 9163-9174.

[10] JENSSEN R. Kernel entropy component analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(5): 847-860.

[11] YANG Y, LI X, LIU X,. Wavelet kernel entropy component analysis with application to industrial process monitoring[J]. Neurocomputing, 2015, 147(1): 395-402.

[12] JIANG Q C, YAN X F, LV Z M,. Fault detection in nonlinear chemical processes based on kernel entropy component analysis and angular structure[J]. Korean J. Chem. Eng., 2013, 30(6): 1181-1186.

[13] 齐咏生, 张海利, 高学金, 等. 基于KECA的化工过程故障监测新方法[J]. 化工学报, 2016, 67(3): 1063-1069. QI Y S, ZHANG H L, GAO X J,. Novel fault monitoring strategy for chemical process based on KECA[J]. CIESC Journal, 2016, 67(3): 1063-1069.

[14] ZHANG H L, QI Y S, WANG L,Fault detection and diagnosis of chemical process using enhanced KECA[J]. Chemometrics and Intelligent Laboratory Systems, 2017, 161: 61-69.

[15] 常鹏, 王普, 高学金. 基于核熵投影技术的微生物制药生产过程监测[J]. 信息与控制, 2014, 43(4):490-494. CHANG P, WANG P, GAO X J. Microbial pharmaceutical process monitoring based on projection kernel entropy component[J]. Information and Control, 2014, 43(4): 490-494.

[16] YAO Y, GAO F. A survey on multistage/multiphase statistical modeling methods for batch processes[J]. Annual Reviews in Control, 2009, 33(2): 172-183.

[17] 赵春晖, 王福利, 姚远,等. 基于时段的间歇过程统计建模、在线监测及质量预报[J]. 自动化学报, 2010, 36(3): 366-374. ZHAO C H, WANG F L, YAO Y,. Phase-based statistical modeling, online monitoring and quality prediction for batch processes[J]. Acta Automatica Sinica, 2010, 36(3): 366-374.

[18] RENYI A. Selected Papers of Alfred Renyi: vol. 2[M]. Budapest:AkademiaiKiado, 1976: 565-580.

[19] CHEN Q, WYNNE R J, GOULDING P,. The application of principal compontent analysis and kernel density estimation to enhance process monitoring[J]. Control Engineering Practice, 2000, 8(5): 531-543.

[20] SILVERMAN B W. Density Estimation for Statistics and Data Analysis[M]. London: Chapman&Hall, 1986.

[21] 邓晓刚, 田学民. 基于非线性主元子空间的故障模式识别方法[J]. 系统仿真学报, 2009, 21(2): 478-481. DENG X G, TIAN X M. Fault pattern recognition based on nonlinear principal component subspace[J]. Journal of System Simulation, 2009, 21(2): 478-481.

[22] 齐咏生, 王普, 高学金, 等. 改进MKPCA方法及其在发酵过程监控中的应用[J]. 仪器仪表学报, 2009, 30(12): 2530-2538.QI Y S, WANG P, GAO X J,. Application of an improved multiway kernel principal component analysis method in fermentation process monitoring[J]. Chinese Journal of Scientific Instrument, 2009, 30(12): 2530-2538.

[23] 钟娜, 邓晓刚, 徐莹. 基于LECA的多工况过程故障检测方法[J]. 化工学报, 2015, 66(12): 4929-4940. ZHONG N, DENG X G, XU Y. Fault detection method on LECA for multimode process[J]. CIESC Journal, 2015, 66(12): 4929-4940.

[24] 马贺贺, 胡益, 侍洪波. 基于马氏距离局部离群因子方法的复杂过程故障诊断[J]. 化工学报, 2013, 64 (5): 1674-1682. MA H H, HU Y, SHI H B. Fault detection of complex chemical processes using mahalanobis distance-based local outlier factor[J]. CIESC Journal, 2013, 64(5): 1674-1682.

[25] BREUING M M, KRIEGEL H, NG R T,LOF: identifying density-based local outliers[J]. Acm Sigmod Record, 2000, 29(2): 93-104.

[26] AGUDO D, FERREY A, FERRER J,. Multivariate SPC of a sequencing batch reactor for wastewater treatment[J]. Chemometrics and Intelligent Laboratory Systems, 2007, 85(1): 82-93.

[27] 刘毅, 王海清. Pensim仿真平台在青霉素发酵过程的应用研究[J]. 系统仿真学报, 2006, 18(12): 3524-3528. LIU Y, WANG H Q. Pensim simulator and its application in penicillin fermentation process[J]. Journal of System Simulation, 2006, 18(12): 3524-3528.

[28] BIROL G, UNDEY C, CINAR A. A modular simulation package for fed-batch fermentation: penicillin production[J]. Computers and Chemical Engineering, 2002, 26(11): 1553-1565.

[29] 张子羿, 胡羿, 侍洪波. 一种基于聚类方法的多阶段间歇过程监控方法[J]. 化工学报, 2013, 64(12): 4522-4528. ZHANG Z Y, HU Y, SHI H B. Multistage batch process monitoring based on a clustering method[J]. CIESC Journal, 2013, 64(12): 4522-4528.

[30] YOO C K, KRIS V. Multivariate nonlinear stastical process control of a sequencing batch reactor[J]. Journal of Chemical Engineering of Japan, 2006, 39(1): 43-51.

[31] SHEN Y, DING S X, HAGHANI A,. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process[J]. Journal of Process Control, 2012, 22(9): 1567-1581.

Fault detection in batch process by multistage multiway kernel entropy component analysis

DENG Xiaogang, ZHANG Chenchen, WANG Lei

(College of Information and Control Engineering, China University of Petroleum, Qingdao 266580, Shandong, China)

A fault detection method,.., multistage multiway kernel entropy component analysis (MsMKECA) was proposed on the basis of nonlinearity and multistage characteristics of batch process.First, in order to divide a batch process into multiple stages, a matrix similarity stage division method was constructed from correlation matrixes of the time-series kernel entropy components. Then, a batch-variable 3-D unfolding technique was introduced to build MKECA model in each stage and to monitor operations in each stage of the batch process, which overcame on-line monitoring impediments of requiring estimation on future values by conventional batch-wise unfolding technique. Simulation study on penicillin fermentation process showed that the proposed method can offer much faster fault detection than traditional MKECA.

fault detection; MKECA; batch process; multistage

10.11949/j.issn.0438-1157.20161501

TP 277

A

0438—1157（2017）05—1961—08

邓晓刚（1981—），男，副教授。

国家自然科学基金项目（61403418, 61273160）；山东省自然科学基金项目（ZR2014FL016）；中央高校基本科研业务费专项资金（17CX02054）。

2016-10-26收到初稿，2017-01-17收到修改稿。

2016-10-26.

DENG Xiaogang, dengxiaogang@upc.edu.cn

supported by the National Natural Science Foundation of China (61403418, 61273160), the Natural Science Foundation of Shandong Province (ZR2014FL016) and the Fundamental Research Funds for the Central Universities(17CX02054).