西江大桥桥位处实测良态风非平稳特性

史康，何旭辉，邹云峰，李欢



西江大桥桥位处实测良态风非平稳特性

史康1, 2，何旭辉1, 2，邹云峰1, 2，李欢1, 2

(1. 中南大学土木工程学院，湖南长沙，410075；2. 中南大学高速铁路建造技术国家工程实验室，湖南长沙，410075)

以南广(南宁—广州)铁路西江大桥风环境监测子系统实测风场数据为研究对象，选择2次强良态风样本，运用经验模态分解法(EMD)和小波分析对强风样本进行非平稳分析，建立基于EMD分解和小波分析的非平稳风速模型，并将其与传统平稳风速模型计算结果对比分析。研究研究表明：西江大桥桥位处良态风非平稳特征明显；采用平稳风模型计算的紊流强度、阵风因子、积分尺度均比相应非平稳风模型计算的大；对于脉动风概率密度分布，非平稳风速模型比平稳模型更符合正态分布假定；2种风速模型计算的顺风向功率谱密度在低频段吻合较好，而在高频段非平稳风模型功率谱密度计算结果小于平稳风模型计算结果；Karman谱在高频段与2种计算模型功率谱密度结果较吻合，但在低频段存在较大差异。

高速铁路；钢箱提篮拱桥；非平稳风速模型；经验模态分解法；小波分析；风特性

风特性的现场实测已成为桥梁风工程的主要研究方法之一，目前国内外进行了较多研究，如：MIYATA等[1]通过日本明石海峡大桥的风速仪记录了 9807号及9918号台风参数；HUI等[2−3]利用桥位侧 50 m高气象站记录了中国香港昂船洲大桥桥位处台风及季风风场特性；谢以顺等[4]通过桥梁风环境监测子系统记录了台风“麦莎”和“卡努”经过润扬悬索桥的全过程；胡俊等[5]结合风场监测环境系统对东海某大跨度悬索桥进行了长期监测。现有研究大多是针对公路桥梁桥址区展开现场实测，对高速铁路桥梁桥位处风场现场实测很少，且在分析过程中将桥位处风速视为平稳随机过程。然而，随着国家高速铁路网的进一步扩展，越来越多的高速铁路桥梁将跨越西部山区峡谷和丘陵地带。相对平坦地区，山区和丘陵地带受复杂地形地貌影响，气流存在切变明显、高紊流度等特点[6−9]，致使该类地形风场呈现更强烈的非平稳特征。若在高速列车行车安全性分析过程中还将风速视为各态历经的平稳随机过程，必将给分析结果带来较大误差，因此，开展高速铁路桥梁桥位处的非平稳风场特性研究具有一定的工程意义。南广(南宁—广州)铁路肇庆西江大桥地处位于广东省肇庆市，是拱脚中心距为 450 m的钢箱提篮拱桥，孔跨布置为(25+50+386+50+49) m，矢跨比为 1/4，桥面距拱顶 73.5 m。拱肋为钢结构，桥面系采用结合梁体系。本文以此为工程背景，依托大桥风环境监测系统，选取拱顶2次/h、平均风速超过 10.8 m/s(强风)且持续时间在 4 h以上的强良风样本，分别运用经验模态分解法(empirical mode decomposition, EMD)和DB10小波建立基于EMD分解和小波分析的非平稳风速模型，并将其与传统平稳风速模型进行对比分析，以便为后续基于非平稳风的风车桥耦合研究提供参考。

1 非平稳风特性分析方法

1.1 平稳风速模型

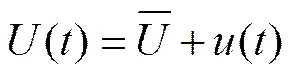
(2)

1.2 非平稳风速模型

非平稳风速模型是依据Gramer分解理论[10−13]，将风速时间序列分解为时变确定性趋势成分和平稳零均值随机成分。因此，可以将顺风向风速分解为时变平均风和零均值的平稳脉动风，而对横风向和竖向风速也可进行类似分解[11]。

顺风向：

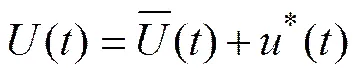
横风向：

(4)

竖向：

1.3 时变平均风提取方法

由以上非平稳风速模型可以看出，如何获得非平稳风速模型中时变趋势项是进行非平稳风特性分析的关键，现有计算方法主要有斜率法、差分法、低通滤波法以及最小二乘拟合法等[12−14]，然而，这些方法均需先假定趋势项的类型。但实际风速时程曲线中趋势一般较难确定，导致用以上方法提取趋势项受到一定限制。目前，对于非平稳风速模型中趋势项的提取多采用经验模态分解法(EMD)[15]与多尺度小波分析[16−17]。EMD常因边端效应问题而影响计算精度，必须采取一定的措施抑制其影响；而小波分析也因种类的选取不同而影响最后计算结果。据文献[18−19]，DB10小波提取的时变平均风计算精度最高，平行延拓不仅算法简单，而且能够有效抑制边端效应。为此，本文 EMD分解运用平行延拓抑制边端效应，小波分析选取 DB10小波提取非平稳时变趋势项，建立基于 EMD分解的非平稳风速模型(简称EMD模型)和基于小波分析的非平稳风速模型(简称小波模型)。

2 风环境监测子系统

西江大桥风环境监测子系统采用4台英国Gill公司的Windsonic型二维超声风速仪，分别布置于桥面上游边跨两侧、跨中及拱顶，南宁(1号)和广州侧(3号)风速仪分别距跨中 270 m和 291 m，拱顶风速仪(4号)距桥面 73.53 m，风速仪编号及具体布置见图 1。Windsonic风速测试范围为 0~60 m/s，量程精度为±2%；风向测试范围为0°~359°，精度为±3°。风速仪采用全天候工作模式，采集频率为 1 Hz。

表1 2种风速模型下相关参数的计算公式

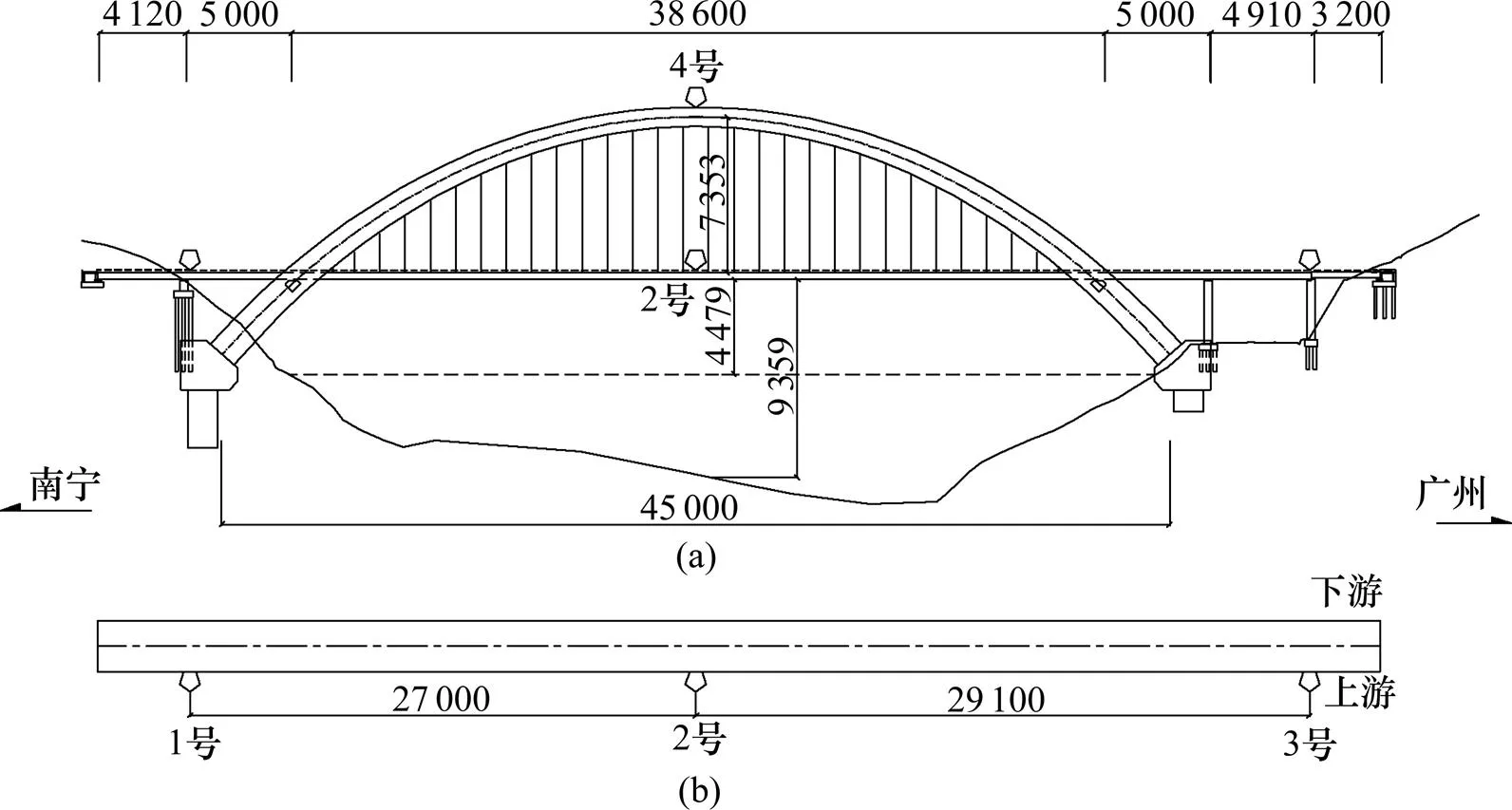
数据单位：cm

3 非平稳风特性分析

3.1 强风样本

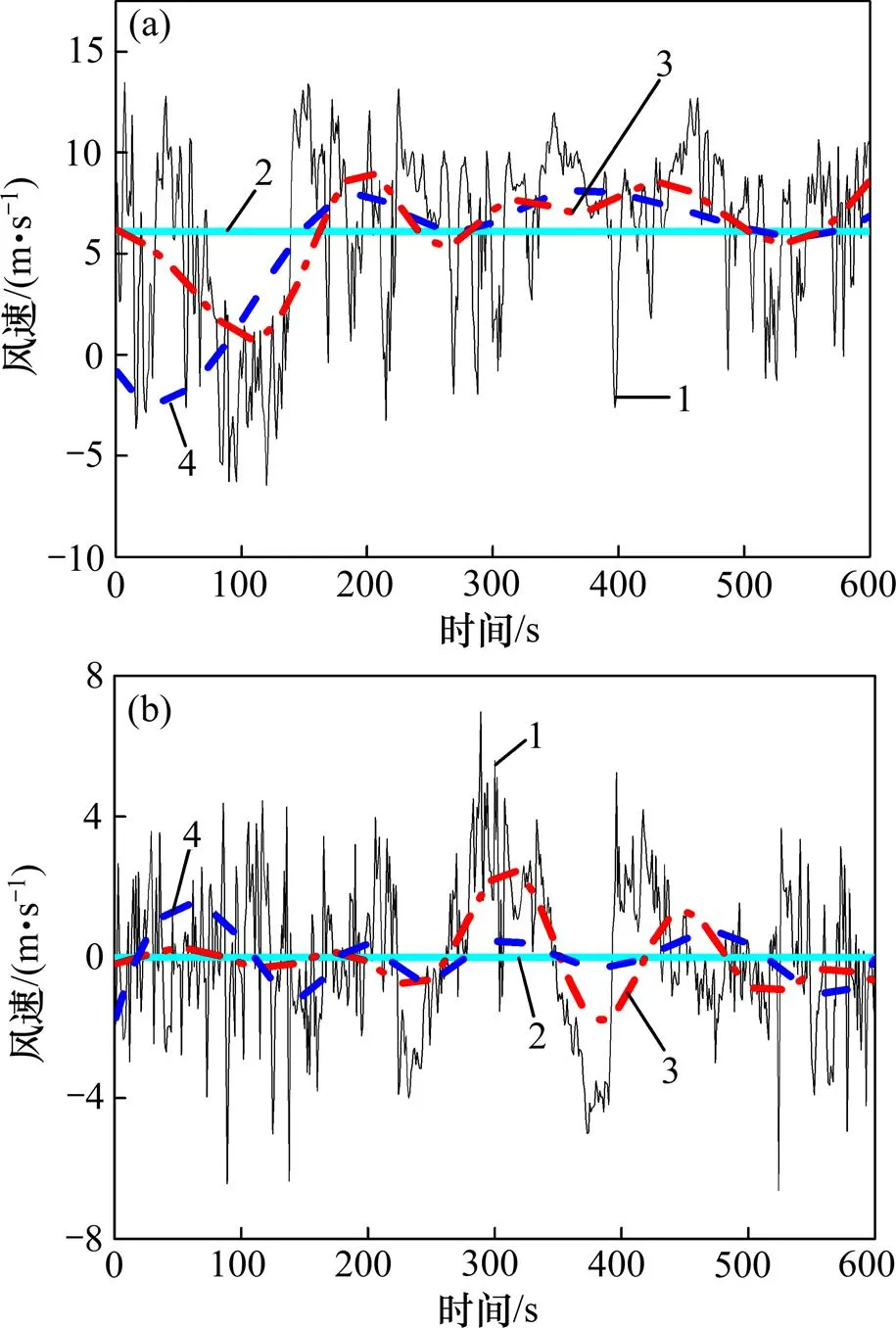
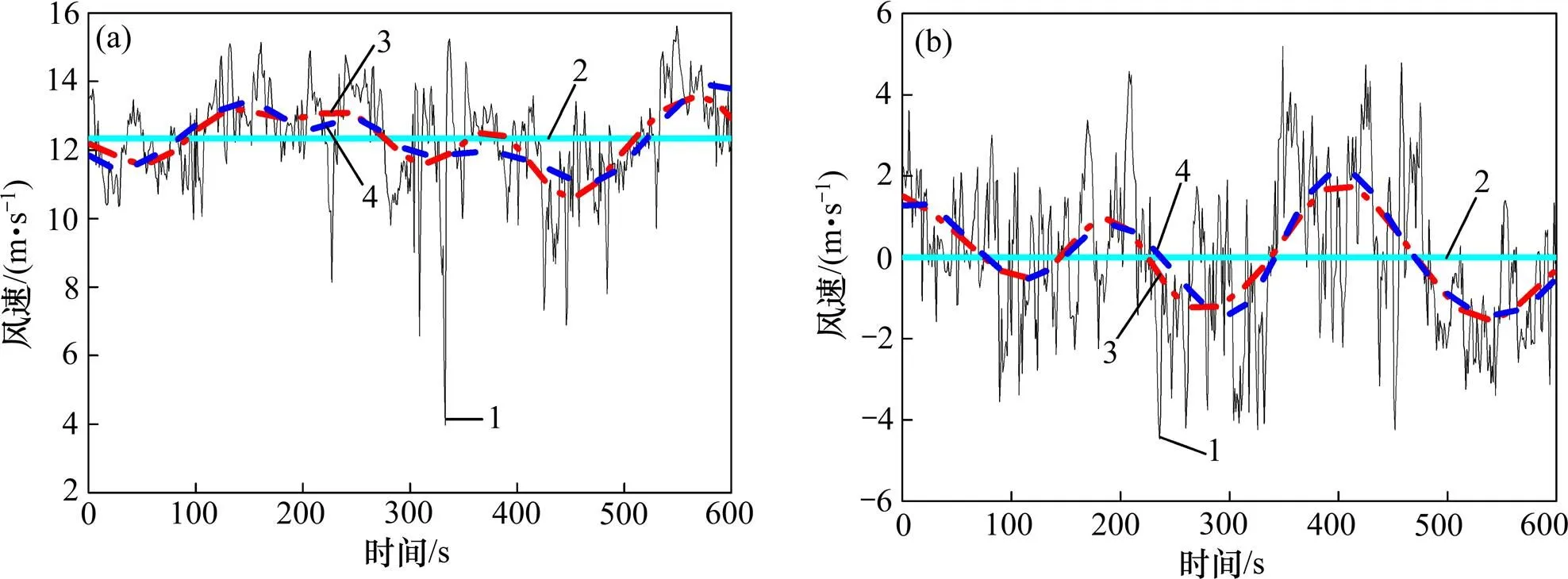
为较真实地获得桥位处良态风非平稳风特性，选择拱顶1 h平均风速大于 10.8 m/s且持续4 h以上的强风样本。根据以上原则，选择了2个强风样本，时段分别为 2014−12−16T2:00—5:00(样本一)和2015−03−17T12:00—15:00(样本二)，每次强风持续时间均为4 h。图2所示为自系统自安装日到2015−03期间1 h内平均风速变化曲线。从图2可知：，样本一 1 h内最大平均风速为 12.06 m/s，样本二1 h内最大平均风速为 13.13 m/s。

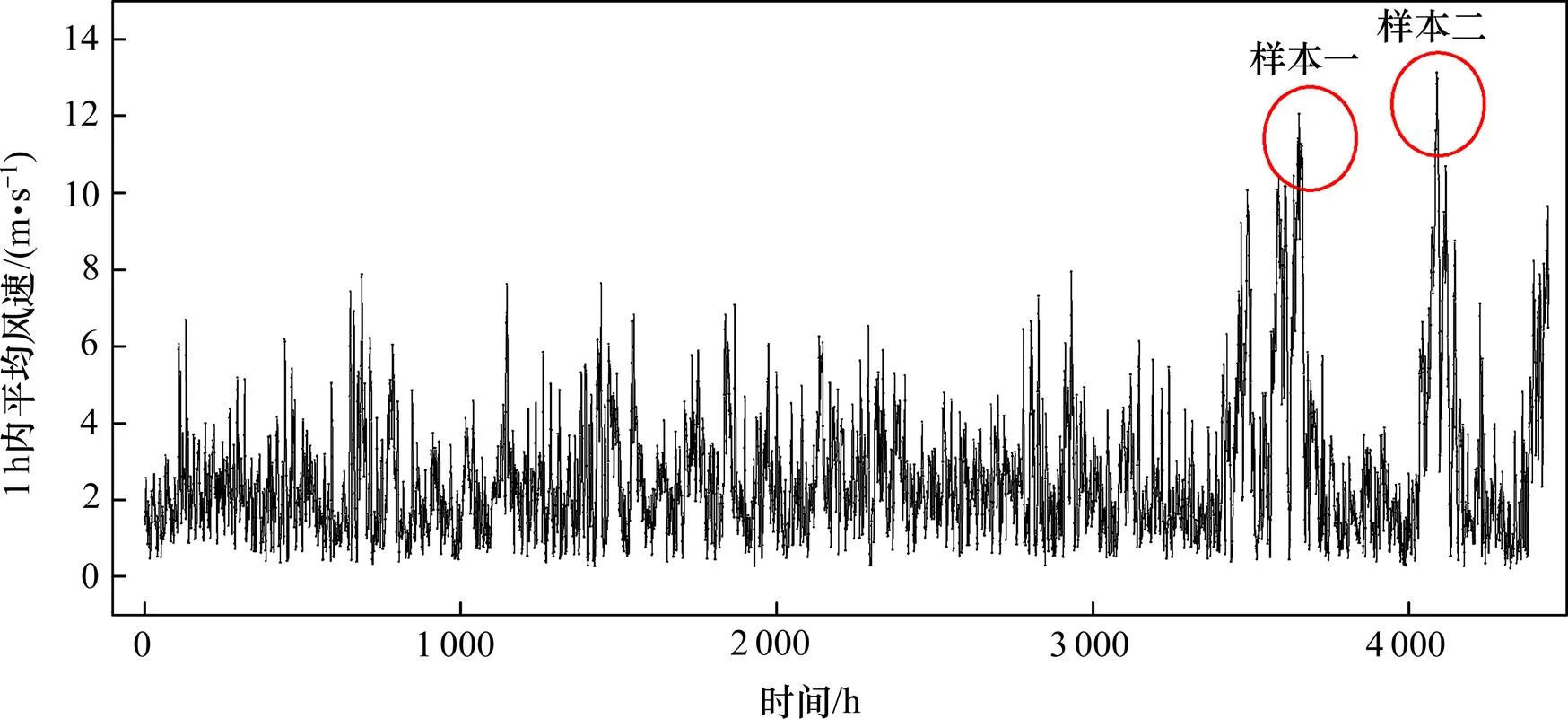
图2 1 h内平均风速变化曲线

3.2 时变平均风

基于以上强风样本，首先对原始数据进行预处理，剔除数据样本中由于各种原因引起的野点干扰，然后以10 min为时距对所有数据进行样本分割(以下数据分析中若没有特别说明，则均以10 min为时距)。随机选择某一段10 min数据样本，运用EMD和小波分析提取趋势项，并将其与传统平稳风模型计算的平均风速进行对比分析，结果如图3~4所示。由图3~4可知：实测样本一和样本二在顺风向和横风向均表现出较明显的非平稳特性，且EMD和小波分析提取时变趋势项基本一致，但与样本一相比，样本二的2种方法提取时变趋势项更吻合，其主要原因是样本二的平均风速更大，EMD抑制端点效应更明显。

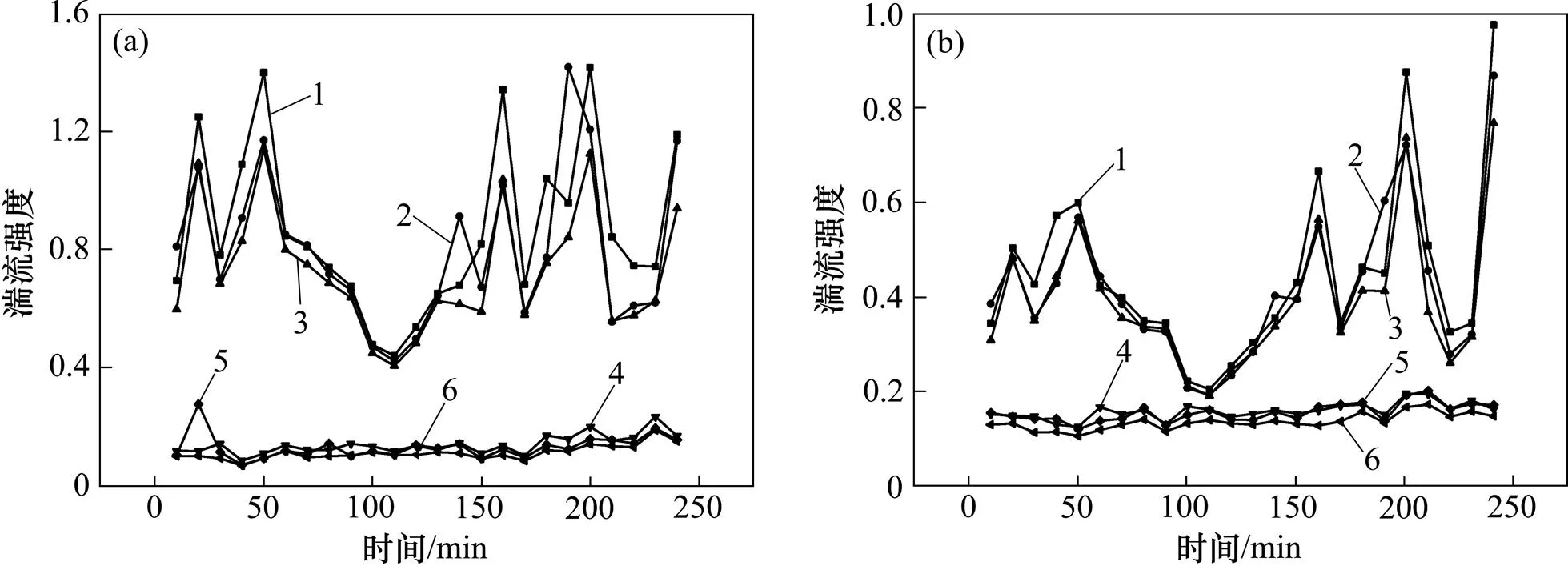
3.3 湍流强度和阵风因子

湍流强度和阵风因子均用于表征风的脉动强度。图5所示为不同计算模型在顺风向和横风向的湍流强度计算值。由图5可知：样本一和样本二的传统平稳风速模型计算的湍流强度均比EMD模型和小波模型的大。对于样本一，基于传统平稳风速模型在顺风向、横风向计算的湍流强度平均值分别为0.868和0.446，而EMD模型的湍流强度计算值分别为0.803和0.417，小波模型计算值分别为0.725和0.393，且不同计算模型顺风向湍流强度分量u均大于横风向湍流强度分量v。虽然样本二的湍流强度计算结果在数值上与样本一有一定差异，但变化趋势与样本一的一致。图6所示为不同计算模型在顺风向和横风向的阵风因子计算值。从图6可见：对于样本一和样本二，传统平稳风速模型计算的阵风因子均比EMD模型和小波模型的大。通过比较以上平稳和非平稳风速模型计算值可知：平稳风速模型高估了现场实测风的脉动特性。

3.4 积分尺度

积分尺度是脉动风中湍流涡旋平均尺度的量度，是反映脉动风特性的又一重要参数。不同风速模型在顺风向和横风向的积分尺度计算值如图7所示。从图7可知：顺风向样本一的平稳风速模型、EMD模型和小波模型的积分尺度计算平均值分别为46.70 m，30.39 m和20.14 m，横风向的积分尺度计算平均值分别为30.46 m，15.88 m和13.32 m；相对于样本一的积分尺度计算值，样本二的积分尺度计算值更大，顺风向平稳风速模型、EMD模型和小波模型的积分尺度计算平均值分别为 161.22 m，102.33 m和59.20 m，而横风向的积分尺度计算值分别为119.33 m，101.36 m和55.33 m。从样本一和样本二的积分尺度计算值均可以看出：小波模型积分尺度计算值最小，传统平稳风速模型的积分尺度计算值最大，其变化趋势与湍流强度和阵风因子的变化趋势一致；平稳风速模型计算值最大约为小波模型的 2.72倍，这说明用平稳风速模型分析非平稳风过程会高估其脉动特性。

(a) 顺风向；(b) 横风向

(a) 顺风向；(b) 横风向

(a) 顺风向；(b) 横风向

(a) 顺风向；(b) 横风向

3.5 概率密度分析

图8所示为样本一和样本二在顺风向和横风向分别采用平稳、非平稳风速模型计算的脉动风概率密度曲线与正态分布拟合曲线。由图8可见：各种风速模型在顺风向和横风向基本上均符合正态分布假设，而相对平稳风速模型，非平稳风速模型更符合正态分布假定，研究结果与文献[20]中结果基本一致。

(a) 顺风向；(b) 横风向

(a) 样本一顺风向；(b) 样本一横风向；(c) 样本二顺风向；(d) 样本二横风向

3.6 功率谱密度函数

功率谱表征湍流能量在频域中的分布，用来描述湍流中不同尺度漩涡的动能对湍流脉动动能的贡献。本文运用Welch法[21]分别计算 EMD模型和小波模型的顺风向功率谱密度函数，并将其与平稳风模型和规范推荐[22]Karman谱对比分析，结果如图9所示。

(a) 样本一；(b) 样本二

由图9可看出样本一和样本二的顺风向功率谱密度函数均表现出以下特征：1) 在低频部分(低于0.001 Hz)，非平稳风速模型的计算结果小于平稳风速模型的计算结果；而在高频部分，2种模型的功率谱密度计算结果基本吻合，其主要原因是在进行EMD和小波分析过程中提取了脉动风的时变趋势项，而时变趋势项一般为长周期部分；2) Karman谱在高频段的计算结果与2种计算模型结果较吻合，但在低频段吻合较差。

4 结论

1) 在统计时段内，实测两强风样本顺风向与横风向风速均表现出较强的非平稳特性。与传统平稳风速模型相比，非平稳风速模型计算的湍流强度强度、阵风因子和积分尺度计算值均偏大，其中平稳风速模型计算积分尺度最大约为非平稳风速模型计算值的2.72倍，表明传统平稳风速模型高估了现场实测风的脉动特性。

2) 采用平稳和非平稳风速计算的脉动风速基本上均符合正态分布假定，而相对于平稳风速模型，非平稳风速模型更符合正态分布假定。

3) 对于实测强风样本顺风向功率谱密度函数，在低频部分(低于0.001 Hz)，非平稳风速模型的功率谱密度计算结果总体小于平稳风速模型的计算结果；而在高频部分，2种模型模型计算结果基本吻合。Karman谱在高频段与2种计算模型结果较吻合，但在低频段吻合较差。

[1] MIYATA T, YAMADA H, KATSUCHI H, et al. Full-scale measurement of Akashi-Kaiyo Bridge during typhoon[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12/13/14/15): 1517−1527.

[2] HUI M C H, LARSEN A, XIANG H F. Wind turbulence characteristics study at the Stonecutters Bridge site: Part Ⅰ: Mean wind and turbulence intensities[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(1): 22−36.

[3] HUI M C H, LARSEN A, XIANG H F. Wind turbulence characteristics study at the Stonecutters Bridge site: Part Ⅱ: Wind power spectra, integral length scales and coherences[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(1): 48−59.

[4] 谢以顺, 李爱群, 王浩. 润扬悬索桥桥址区实测强风特性的对比研究[J]. 空气动力学学报, 2009, 27(1): 47−51. XIE Yishu, LI Aiqun, WANG Hao. Comparison study on experimental strong wind characteristics of Runyang Suspension Bridge[J]. Acta Aerodynamica Sinica, 2009, 27(1): 47−51.

[5] 胡俊, 欧进萍. 基于长期监测数据的某悬索桥桥位近处风场特性分析[J]. 中南大学学报(自然科学报), 2013, 44(7): 2989−2996. HU Jun, OU Jinping. Wind field characteristics analysis at a long-span suspension bridge based on long-term monitoring data[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2989−2996.

[6] CAO Shuyang, TAMURA T. Experimental study on roughness effects on turbulent boundary layer flow over a two-dimensional steep hill[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94(1): 1−19.

[7] CAO Shuyang, TAMURA T. Effects of roughness blocks on atmospheric boundary layer flow over a two-dimensional low hill with/without sudden roughness change[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(8): 679−695.

[8] 何旭辉, 秦红禧, 邹云峰, 等. 台风外围影响下的大跨度拱桥桥址区近地风特性实测研究[J]. 湖南大学学报(自然科学版), 2017(1): 23−31. HE Xuhui, QIN Xihong, ZOU Yunfeng, et al. Field measurement and investigation of wind characteristics at the site of a long-span arch bridge in the periphery of typhoon Kujira[J]. Journal of Hunan University (Natural Sciences), 2017(1): 23−31.

[9] WANG Xu, HUANG Peng, YU Xianfeng, et al. Wind characteristics near the ground during typhoon Meari[J]. Journal of Zhejiang University: Science A (Applied Physics & Engineering), 2017(1): 33−48.

[10] CHEN Jun, HUI M C H, XU Youlin. A comparative study of stationary and non-stationary wind models using field measurements[J]. Boundary-layer Meteorology, 2007, 122(1): 105−121.

[11] CHEN Jun, XU Youlin. On modelling of typhoon-induced non-stationary wind speed for tall buildings[J]. The Structural Design of Tall and Special Buildings, 2004, 13(2): 145−163.

[12] XU Youlin, CHEN Jun. Characterizing nonstationary wind speed using empirical mode decomposition[J]. Journal of Structural Engineering, 2004, 130(6): 912−920.

[13] 孙海, 陈伟, 陈隽. 强风环境非平稳风速模型及应用[J]. 防灾减灾工程学报, 2006, 26(1): 52−57. SUN Hai, CHEN Wei, CHEN Juan. Nonstationary wind speed model and its application in strong winds[J]. Journal of Disaster Prevention and Mitigation Engineering, 2006, 26(1): 52−57.

[14] BENDAT J S, PIERSOL A G. Random data: Analysis and measurement procedures[M]. 2nd ed. Wiley, 1986: 1−30.

[15] 陈隽, 徐幼麟. 经验模分解在信号趋势项提取中的应用[J]. 振动,测试与诊断, 2005, 25(2): 101−104. CHEN Juan, XU Youlin. Application of EMD to signal trend extraction[J]. Journal of Vibration, Measurement & Diagnosis, 2005, 25(2): 101−104.

[16] 朱学锋, 韩宁. 基于小波变换的非平稳信号趋势项剔除方法[J]. 飞行器测控学报, 2006, 25(5): 81−85. ZHU Xuefeng, HAN Ning. Removal of trend from non-stationary signal based on wavelet transformation[J]. Journal of Spacecraft TT & C Technology, 2006, 25(5): 81−85.

[17] 申建红, 李春祥, 李锦华. 基于小波变换和EMD提取非平稳风速中的时变均值[J]. 振动与冲击, 2008, 27(12): 126−130. SHEN Jianhong, LI Chunxiang, LI Jinhua. Extracting time-varying mean of the non-stationary wind speeds based on wavelet transform (WT) and EMD[J]. Journal of Vibration and Shock, 2008, 27(12): 126−130.

[18] 方俊. 基于小波分析的斜拉桥拉索风雨振非平稳性研究[D]. 长沙: 中南大学土木工程学院, 2010: 35−39. FANG Jun. Study on nonstationary characteristics of wind-rain-induced vibration of stay cables based on wavelet analysis[D]. Changsha: Central South University. School of Civil Engineering, 2010: 35−39.

[19] 徐斌, 徐德城, 朱卫平, 等. 希尔伯特−黄变换方法的改进[J]. 西北工业大学学报, 2011, 29(2): 268−272. XU Bin, XU Decheng, ZHU Weiping, et al. Improving Hibert-Huang transform method[J]. Journal of Northwestern Polytechnical University, 2011, 29(2): 268−272.

[20] 申建红, 李春祥, 李锦华. 基于小波变换和EMD提取非平稳风速中的时变均值[J]. 振动与冲击, 2008, 27(12): 126−130. SHEN Jianhong, LI Chunxiang, LI Jinhua. Extracting time-varying mean of the non-stationary wind speeds based on wavelet transform(WT) and EMD[J]. Journal of Vibration and Shock, 2008, 27(12): 126−130.

[21] 赵静, 刘琦. Welch法谱估计和参数模型谱估计的MATLAB分析[J]. 水利电力机械, 2006, 28(4): 48−50. ZHAO Jing, LIU Qi. Analysis of Welch method and parameter model spectrum estimation by MATLAB software[J]. Water Conservancy & Electric Power Machinery, 2006, 28(4): 48−50.

[22] JTG/TD 60-01—2004, 公路桥梁抗风设计规范[S]. JTG/TD 60-01—2004, Wind-resistent design specification for highway bridges[S].

(编辑 陈灿华)

Nonstationary wind characteristics of wind speed of normal climate at Xijiang bridge site

SHI Kang1, 2, HE Xuhui1, 2, ZOU Yunfeng1, 2, LI Huan1, 2

(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China)

Based on wind environment monitoring system of Nanning—Guangzhou railway of Xijiang bridge and taking its measured wind field data as the research object, two strong wind samples were chosen. The empirical mode decomposition (EMD) and wavelet analysis methods were applied to analyze nonstationary wind characteristics for these two samples. The nonstationary wind speed models were established by EMD and wavelet analysis methods. Moreover, comparisons were made between traditional wind speed model and nonstationary models. The results show that nonstationary characteristics at Xijiang bridge site are significant and the calculated values of turbulence intensify, gust factor, integral scales by using traditional wind speed model are larger than those by nonstationary models. With respect to probability density distribution of pulsating wind speed, nonstationary models fit well with the assumption of normal distribution in comparison to stationary model. The longitudinal power spectral density is in good agreement at low frequencies by using these two kinds of models, while the calculation values of nonstationary model is less than those of stationary model at high frequencies. Karman spectrum is in good agreement with the results of nonstationary and stationary models, but there exists bigger difference at low frequency.

high-speed railway; steel box X-style arch bridge; non-stationary wind speed model; empirical mode decomposition(EMD); wavelet analysis; wind characteristic

10.11817/j.issn.1672-7207.2017.05.030

U238

A

1672−7207(2017)05−1352−08

2016−05−19；

2016−07−01

国家自然科学基金资助项目(51178471，51322808)；教育部新世纪优秀人才支持计划项目(NCET-12-0550)；长江学者和创新团队发展计划项目(IRT1296)；中国博士后科学基金资助项目(2014M562133) (Projects(51178471, 51322808) supported by the National Natural Science Foundation of China; Project(NCET-12-0550) supported by the New Century Excellent Talents Program in University; Project(IRT1296) supported by the Program for Changjiang Scholars and Innovation Research Team in University; Project(2014M562133) supported by China Postdoctoral Science Foundation)

史康，博士研究生，从事桥梁风环境监测与抗风研究；E-mail: 478491139@qq.com