指数型寿命分布产品无故障试验数据分析评估方法

付朝晖



指数型寿命分布产品无故障试验数据分析评估方法

付朝晖

(昆明船舶设备研究试验中心, 云南昆明, 650051)

武器装载可靠度试验经常产生无故障试验数据, 利用指数分布的无记忆性, 通常认为同类型的个产品的无故障试验时间等同于同一产品无故障工作了个产品试验时间的总和。在工程应用中, 这种方法存在局限性。文中利用浴盆曲线解释了不能完全采用这种方法进行计算的原因, 即在装载总时间达到进入损耗失效条件的时候, 该方法存在错误。针对这一关键问题, 提出了装载可靠度计算的修正方法, 给出了置信下限分析, 结合算例验证了该方法的可行性。

武器; 装载可靠度试验; 指数分布; 寿命; 无故障; 置信下限; 评估

0 引言

在可靠性试验中, 经常会采用截尾试验方式, 获得各种截尾数据。随着科学技术的发展, 鱼雷等产品的可靠性越来越高, 在试验中会获得“无失效数据(zero-failure data)”。对于无失效数据可靠性研究, 已经有了无失效可靠性抽样检验方法、最优置信限发、配分布曲线法、极小法、修正似然函数法、等效失效数法、参数的综合估计法等[1]。Sun W[2]等人提出的无失效数据情形下可靠性参数最优置信下限的方法为鱼雷装载可靠度试验应用提供了基础。特别针对指数分布情况下的无失效数据分析, 许多人都开展了相关方面的研究[3-9], 给出了平均寿命、可靠度和可靠寿命的估计。但是, 对于在计算过程中其失效规律会发生变化情况的研究还较少, 使得在鱼雷装载可靠度试验中的工程计算方法还存在一些值得商榷之处。

在应用这些方法的过程中, 几乎都忽略了这些方法的前提, 即产品必须服从某种分布。例如, 目前在工程应用领域, 许多装备的寿命都被认为是服从指数分布[10-12]。做出这种假设的一个很重要的原因是: 指数分布的特性可以使可靠性研究和分析工作极大的简化, 从而避免了其他分布会遇到的很多难以解决的概率与统计问题。而指数分布的无记忆性则是其特性的一个重要方面, 所谓的无记忆性在装备可靠性计算中即无故障的产品可以合并为一个产品。由此就出现了个独立同指数分布的产品, 若在试验中都未发生故障, 则可以等同于一个产品工作了个产品工作时间的总和而无故障。根据这个特性进行推理, 就可以得到这样一个结论, 即在鱼雷装载可靠性试验时, 如果有8条产品直接进行装载, 每1条产品在鱼雷发射管内装载3个月后无故障, 则可以认为鱼雷产品装载24个月(即2年, 8×3个月)无故障。再进一步, 如果是80条产品, 则会得出鱼雷发射管内装载240个月, 即20年无故障的这样一个难以置信的结论, 这个指标是国内目前任何一个工业部门没有达到的。其实, 上述推理假设产品服从指数分布和利用该分布的无记忆性都没有问题, 问题在于鱼雷产品的无故障时间能不能直接简单合并。实际上, 这种直接合并的做法是有前提条件的, 并不是针对任意的产品都可以。以下将针对这一问题进行分析。

1 指数分布的无记忆性

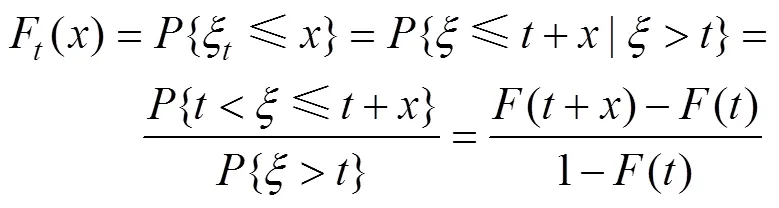
综合式(1)和式(2), 可以得到指数分布产品的剩余寿命

(3)

由此可见, 指数分布产品从某一个时刻开始, 仍旧符合指数分布。通过这一个性质, 可以将任意一个无故障的产品当作是另外一个产品的前面部分。依次类推, 就可以将无故障的个产品合并为一个产品, 这个结论可以从概率上得到证明。

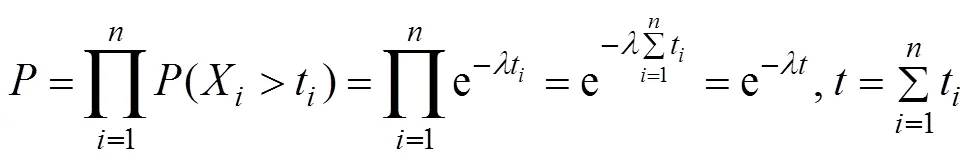
上述推断就是装备评估计算时的试验时间“合并”的依据, 但这种推理在实际上忽略了电子产品失效率的一般规律, 即通常所说的“浴盆曲线”。在不同的时间段, 其失效率是在不断变化的, 而不是认为在所有的时间内都是常数。

2 产品的失效率规律

产品的失效率一般是随着时间的变化而变化的。根据长期实践的经验, 一般在工程上认为大多数失效率函数的曲线都是呈现浴盆截面形状, 如图2所示, 称之为“浴盆曲线”。此曲线左边部分称之为早期失效期。在此期间指出, 产品的失效率高, 随着时间的推移, 表现出急速下降的形态。曲线当中平坦的部分称为偶发失效期, 进入这个期间内, 产品的失效率已经趋于稳定。产品最右边的部分是损耗失效期, 这个期间内, 产品由于使用日久而逐渐磨损, 失效率逐渐增加。一般在进入定型阶段的装备, 都认为是处于中间的偶发失效的阶段, 其特点是失效率为常数, 失效分布为指数分布, 其可靠度与失效率有如下的关系

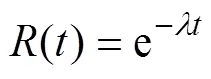
若产品分布适合指数分布, 根据无记忆性, 使得累计时间通常使用数量和每一个时间的乘积, 这种方法存在不足。浴盆曲线有一个时间处于早期/耗损失效, 如果无限使用数量与单个数量乘积的做法则忽略了浴盆曲线的早期/耗损失效。例如每一个产品搁置1个月, 合格, 如果有10 000个产品同时试验, 显然其时间不能是10 000个月, 即800多年。

2.1 原因分析

通过上面简单的推论, 可以知道指数型寿命分布产品的无故障使用时间是不能够简单叠加的, 至少是不能够无限叠加, 它有一个上限。其实, 仅仅在图2中的区间之内, 产品的规律才是符合失效率为一个常数的, 此时式(4)才成立。超过了这个区间, 产品的失效率会在短时间内剧增, 并已处于早期失效和损耗失效阶段。在这个阶段, 如果再次加入新的产品, 其无故障使用时间不但不会增加, 反而会不断地减少, 这也可以从概率上得到证明。

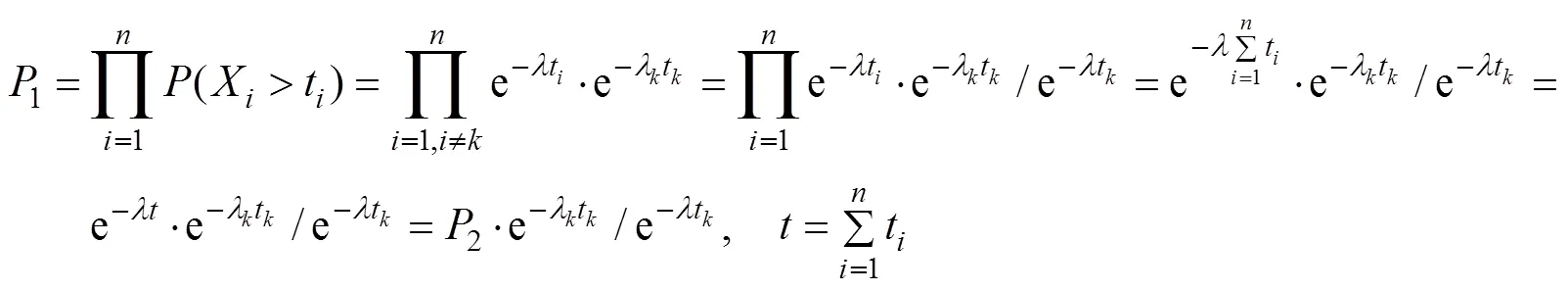
2.2 无故障产品寿命置信下限计算

通过分析与计算可知, 对于无故障产品的寿命而言, 即使是服从指数分布, 直接合并还是需要慎重。目前, 对于无故障数据分析研究受到了工程界和统计学者的广泛重视, 取得了不少进展, 陈家鼎[9]等关于无失效数据情形下置信限的讨论是其中的代表性成果。针对具体的指数分布, 其计算如下。

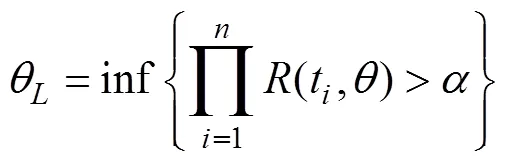
即

(8)

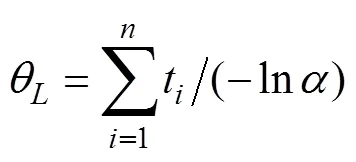
(10)

上述计算是在工程上的应用, 实际上就是基于总工作时间不大于耗损失效时间的, 即

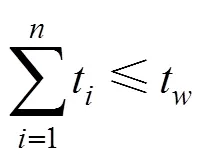
一旦不满足式(11), 对于平均寿命和可靠度的计算方式有待商榷。若不满足式(11), 不妨假设, 由此可以等效的认为, 在时间内的产品符合失效率相同的分布, 而超出部分时间产品的失效率记作, 通过浴盆曲线可知, 随着增加,也显著增加, 即。由此式(7)转化为

(12)

即

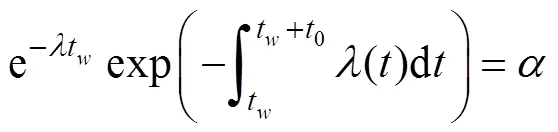
解上述方程, 可得

(14)

2.3 无故障产品寿命置信下限分析

因此, 当累计试验时间超过了浴盆曲线偶发试验时间界限(即时刻)时, 增加样品数量虽然不能简单的进行“试验时间合并”, 但是累计试验时间长的试验所证明的产品平均寿命相对长一些。对于超过了偶发试验时间界限之后的时间, 可研究其等效于偶发失效的时间, 从而继续利用式(10)进行计算。

2.4 计算实例

在《鱼雷通用规范》(GJB531B-2012)中, 对于鱼雷装载可靠度试验样品数目规定不少于6条, 具体数目可由承制方与定购方根据考核要求确定。因此可假设6条鱼雷产品同时进行装载可靠度试验, 试验采取定时截尾方式, 时间为6个月, 均未出现故障。并且为了计算方便, 假设鱼雷产品装载18月后, 其失效率将明显变化, 变化规律为在基准失效率的基础上呈指数增加, 底数为2。

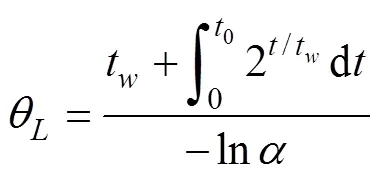
由此, 可以得到在实际试验过程中, 实际的试验时间存在一个等效因子, 折算之后, 可以继续进行时间的简单合并, 其具体的等效性因子

(16)

由图3可知, 当试验总时间超过了偶发失效的时间界限之后, 相应的试验时间需要经过折算, 方可继续进行计算。例如, 累计超过时间界限约236个月, 折算后的时间仅为60个月。为了更加直观的理解试验时间的等效关系, 在无故障和每一个样本试验时间为6个月的前提条件下, 试验样本量的等效关系计算如图4所示。

由图4可知, 在不同的阶段, 等效试验样本量增多, 需要的实际样本量急剧增加。为了得到最佳的等效性效果, 其实际的样本量大约在5~10 之间, 这也与《鱼雷通用规范》(GJB531B-2012)规定的样本量不小于6条是符合的。

3 结束语

通过对产品失效率浴盆曲线的分析, 解释了目前装载可靠度验证试验数据计算中存在一个误区, 并且证明了随着产品数量的增加, 其计算结果就越失真。该方法虽然给出了平均寿命计算的修正公式, 但是在总试验时间大于(偶发失效和损耗失效的间隔时间)条件下, 所得到的置信最优置信下限存在依赖于产品的耗损失效率曲线, 在工程上计算不方便。不同产品的损耗失效曲线并不相同, 究竟样本量为多少才是最优, 样本量与可靠度的关系等问题还有待于后续进一步研究。

[1] 韩明. 无失效数据可靠性进展[J]. 数学进展, 2002, 31(1): 7-19.Han Ming. The Advances of Reliability for Zero-Failure Data[J]. Advances Mathematics, 2002, 31(1): 7-19.

[2] Sun W, Chen J. Some New Results on the Confidence Limits for Reliability Parameters in the Case of No Failures[J]. Systems Science and Mathmatical Sciences, 1999, 12(1): 70-81.

[3] 赵海兵, 程依明. 指数分布场合下无失效数据的统计分析[J]. 应用统计概率, 2004, 20(1): 59-65.Zhao Hai-bing, Cheng Yi-ming. Staistical Analysis about Zero-failure Data Using Memoryless Property of Exponential Distribution[J]. Journal of Applied Probalibility and Statistics, 2004, 20(1): 59-65.

[4] 郭念国, 徐昕, 焦万堂. 指数分布场合下无失效数据分析[J]. 郑州轻工业学院学报(自然科学版), 2008, 23(5): 117-120.Guo Nian-guo, Xu Xin, Jiao Wan-tang. Staistical Analysis about Zero-failure Data with Exponential Distribution[J]. Journal of Zhengzhou University of Light Industry (Natural Science), 2008, 23(5): 117-120.

[5] 郇正良. 指数分布下无失效数据的统计分析[J]. 山东农业大学学报(自然科学版), 2001, 23(1): 363-367.Xun Zheng-liang. The Staistical Analysis of Zero-failure Data of Exponential Distribution[J]. Journal of Shandong Agricultural University(Natural Science), 2001, 23(1): 363-367.

[6] 任海平, 李中恢. 指数分布的无失效数据的Bayes统计分析[J]. 井冈山学院学报, 2007, 28(12): 60-70.Ren Hai-ping, Li Zhong-hui. Bayes Staistical Analysis for Zero-Failure Data of Exponential Distribution[J]. Journal of Jinggangshan University(Natural Science), 2007, 28(12): 60-70.

[7] 刘永峰, 郑海鹰. 无失效数据的统计分析[J]. 浙江大学学报(理学版), 2012, 39(3): 273-277.Liu Yong-feng, Zheng Hai-ying. Statistical Analysis about Zero-failure Data[J]. Journal of Zhejiang University (Science Edition), 2012, 39(3): 273-277.

[8] Chen Jia-ding, Sun Wan-long, Li Bu-xi. The Confidence Limits for Reliability Parameters in the Case of No Failure Data[J]. Proceoaing of the Asian Conference on Sta. Com, 1993, 17-20.

[9] 陈家鼎, 孙万龙, 李补喜. 关于无失效数据情形下的置信限[J]. 应用数学学报, 1995, 18(1): 90-100.Chen Jia-ding, Sun Wan-long, Li Bu-xi. On the Confidence Limits in the Case of No Failure Data[J]. Acta Ma- thematicae Applicatae Sinica, 1995, 18(1): 90-100.

[10] 焦志刚, 岳明凯. 弹药可靠性工程[M]. 北京: 国防工业出版社, 2013.

[11] 刘春和, 陆组建, 刘雷锋. 装备可靠性评定方法[M]. 北京: 宇航出版社, 2009.

[12] 赵宇. 可靠性数据分析[M]. 北京: 国防工业出版社, 2014.

(责任编辑: 许 妍)

Evaluation Method of Failure Free Test Data for Exponential Life Distribution Products

FU Zhao-hui

(Kunming Shipborne Equipment Research and Test Center,Kunming 650051, China)

The reliability test of weapon loading often produces failure free test data. By making use of the memoryless of exponential distribution, it is generally considered that the failure free test time ofsame-type products is equal to the total test time ofproducts for one product to work without failure. In engineering applications, however, this method has limitation. This paper explains the reason why this method cannot be fully used for calculation by making use of the bathtub curve, that is, there is a mistake when the total load time is up to the failure condition. To solve this problem, a modified method for calculating the reliability of loading is proposed, and the lower confidence bound is given. The feasibility of the proposed method is verified by an example.

weapon; loadingreliability test; exponential distribution; life; failure free; lower confidence bound; evaluation

10.11993/j.issn.1673-1948.2017.01.011

TJ630.1; TB114.37

A

1673-1948(2017)01-0054-05

2016-10-20;

2016-12-22.

付朝晖(1983-), 男, 硕士, 工程师, 主要研究方向为试验数据分析处理技术.