基于无迹卡尔曼滤波器的改进SLAM问题求解方法①

吴 勇, 关胜晓



基于无迹卡尔曼滤波器的改进SLAM问题求解方法①

吴 勇, 关胜晓

(中国科学技术大学信息科学技术学院, 合肥 230027)

目前在即时定位与地图构建(Simultaneous Localization And Mapping, SLAM)的研究中已经使用局部取样策略来降低无迹卡尔曼滤波(Unscented Kalman Filter, UKF)的计算复杂度至状态向量维数的平方等级. 但是在大规模的SLAM中平方复杂度仍然难以满足实时性需求. 为了解决这个问题, 提出了一种收缩无迹卡尔曼滤波器(Shrink Unscented Kalman Filter, S-UKF), 并应用于SLAM问题中. 首先证明了解耦非线性系统中的部分取样策略和全取样策略的等价性. 然后提出了一个通过重构公式中相关项的收缩方式来降低计算复杂度. 最后, 仿真实验的结果和基于真实环境数据集的实验结果证明了该方法的有效性.

SLAM; 无迹卡尔曼滤波(UKF); 局部取样; 计算复杂度

1　引言

同步定位与地图构建(SLAM)是指自主车辆或移动机器人在未知的环境中构建地图并使用构建的地图同步定位自己的位置[1]. 相比于常规的自主导航系统(例如GPS和地图匹配), SLAM不需要任何外部设备或者关于环境的任何先验信息, 这使得SLAM尤其适用于无GPS环境的机器人导航中. 正是由于SLAM的这些特点, 使得它在过去的20年间受到极大的关注[2-5].

基于前人的理论工作[6,7], 已经发展出种类繁多的基于滤波的方法来解决SLAM问题, 例如扩展卡尔曼滤波器(Extended Kalman Filter, EKF)[8]、无迹卡尔曼滤波器(UKF)[9]、以FastSLAM而闻名的粒子滤波器(Particle Filter, PF)[10]以及稀疏扩展信息滤波器(Sparse Extended Information Filter, SEIF)[11]. 其中EKF有着相对较低的计算成本, 这使得它在实际中已经被广泛应用[3,7]. 但是, 在基于EKF的SLAM中需要将系统线性化以及计算雅可比矩阵, 这会导致性能的降低甚至使滤波发散. 同样的问题也会出现在SEIF中. 与此相反, 在基于取样的滤波算法中使用一组样本和权重来估计状态向量, 不需要线性化和计算雅可比矩阵. 其缺点则是增加了一个附加的计算复杂度. 与FastSLAM相比, 基于UKF的SLAM使用确定性取样和权重, 不会有退化问题. 因而, 如果UKF的计算成本可以显著降低那么它就是一个切实可行的选择.

前人在基于UKF的SLAM中研究了很多方法. Holmes等人[12]提出了一种基于UKF平方根(Square-Root Unscented Kalman Filter, SRUKF)的方法用来解决monoSLAM(Monocular SLAM)问题, 其中使用协方差矩阵的平方根参与递推运算, 避免了在每次迭代步骤中O(N3)复杂度的分解. 尤其是通过重排序状态向量的方法这种计算代价可以降低到O(N2), 其中N是状态向量的维度. 在静态环境下的SLAM过程中, Andrade-Cetto等人[13]提出局部无迹变换(Unscented Transformation, UT)的策略, 其中使用UKF来估计运动过程中车辆的位姿, 使用常规EKF来更新全局的状态向量. 但是, 在迭代步骤中仍然需要线性化来预测相关性. 为了避免线性化, Huang等人[14]提出了基于线性回归模型的局部取样的策略. 这项研究表明, 雅可比矩阵可以从σ点推断出来. 然后, UKF就可以被表示为一个基于线性回归模型, 复杂度为O(N2)的滤波形式. 然而这项工作却没有明确分析局部取样策略相对于全取样策略的效果.

受到文献[8]中研究的启发, 我们指出了基于UKF的SLAM可以被收缩从而显著降低其计算成本. 本文的主要贡献如下:

① 证明了局部取样策略提供了完全相同的车辆姿态估计, 和路标的数目无关;

② 提出了一个基于UKF的SLAM的收缩实现(S-UKF), 复杂度为O(NL2), 其中NL是局部地图中的路标数;

③ 通过仿真和真实环境的数据集来展示基于S-UKF的SLAM的效率.

2 基于UKF的SLAM

在本节中, 我们通过公式给出了基于滤波方式解决SLAM问题的简要概述, 然后是一个基于UKF解决方案的介绍.

2.1 SLAM简述

由于车辆的位置和方向之间的耦合, 所以SLAM是一个非线性估计问题. 在基于滤波的SLAM中, 问题通常表示为状态空间模型, 其中状态向量由机器人当前位姿和环境中所有观察到的路标位置组成. 对于二维的平面SLAM, 令表示时刻机器人的水平位置和方位角, 令表示所有被观测到的路标, 其中表示路标的数量. 离散非线性运动方程一般可表示为:

在SLAM系统中并没有绝对的观测结果, 所以通过使用外感受性的传感器例如激光雷达或者摄像头来获得机器人和环境之间的相对测量值, 并以此值来校正状态的估计. 观测模型如下:

2.2 基于UKF的解决方案

在SLAM中, 为了进行有效的近似非线性变换, UKF首先计算点以及归一化权重以得到状态向量的分布. 然后变换这些点来估计非线性变换. 在预测阶段, 一组点及权重能由如下式(5)计算:

在观测值更新阶段, 观测值的预测分布也可以类似的如下计算:

3 局部取样的一致性

在SLAM问题中, 每个阶段的非线性变换中只会出现部分状态, 因此局部取样策略是用来降低复杂度的一个很有吸引力的选择. 在文献[13]中, 基于标准的UKF的SLAM中, 仅仅基于车辆位姿的UT变换的实验结果表明其低估了协方差矩阵随着路标数的增长而增长的速度. 那么, 局部取样策略的效果如何呢?

3.1 一致性

引理1. 考虑一个非线性变换可分成两个完全分离的非线性部分和线性部分, 如下所示:

那么不论是对全取样策略还是对局部取样策略UKF和常数缩放因子就能提供一个完全相同的关于的估计值. 即该估计值独立于的大小.

图1 使用基于完全取样和局部取样策略的UKF针对不同的路标进行坐标转换的估计实验. 虚线圆和实线圆分别表示蒙特卡罗和UKF在3σ范围内的椭圆.

为了验证非线性估计算法的性能, 一个典型的方法就是极坐标系到笛卡尔坐标系的转换[13,15]. 设定观测量的均值和协方差矩阵分别为, 图1展示了基于不同取样策略的UKF算法的结果, 其中不同的路标分别被增广到状态向量. 尽管在1000个样本下, UKF和蒙特卡罗方法的结果存在不同之处, 但是无论取样策略是什么, 路标的数目是多少, UKF的结果全部相同.

3.2 重构UKF公式

基于引理1, 我们就能够重写点集和权重如下:

将式(22)和式(27)代入式(26), 得到

在更新阶段, 我们也能类似地重写式(12)如下:

我们注意到如果在预测阶段将控制输入向量也考虑进来的话, 那么可以将该向量添加到非线性部分从而得到同样的结果.

4 基于S-UKF的SLAM

正如文献[17]中描述的那样, UKF是一个线性回归卡尔曼滤波器. 而且该线性回归模型已经成功的被应用到UKF中, 并且在文献[14]中用来做可观测性分析. 因此根据上一节的结果我们就能将UKF表达为一个近似线性形式, 然后S-UKF就像压缩扩展卡尔曼滤波器(Compressed Extended Kalman Filter, CEKF)[8]一样被应用.

根据SLAM中传感器的测量范围, 全局地图能够被分为两个单独的部分如图2所示. 相应地, 状态向量和协方差矩阵能被表示如下:

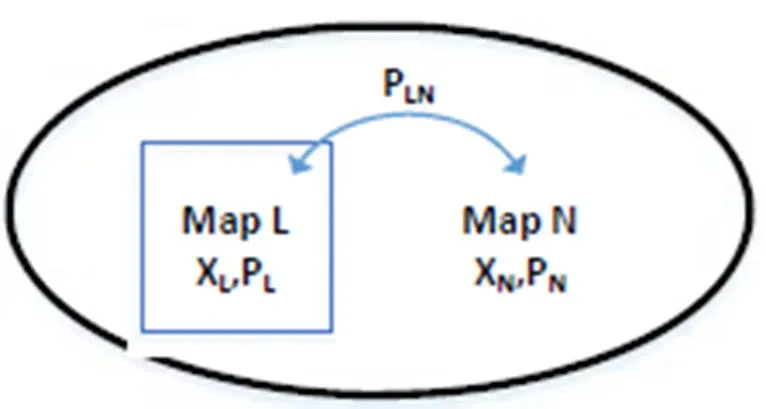
图2 局部和邻居地图

类似地, 在路标初始化阶段, 我们能够通过式(30)得到局部线性因子, 则全局线性因子为:

① 预测阶段

② 局部更行阶段

③ 路标初始化阶段

④ 全局更新阶段

5 实验结果与分析

在本节中, 我们进行了仿真和真实环境数据集实验, 以评估该算法的性能. 所有的实验都是在一台主频2.20GHz的AMD处理器, 2GB内存, 装有Matlab2012a的计算机上实现的. 在这些实验中, 范围测量传感器用来提供测量数据. 为了更加全面的比较, 我们也分别实现了基于EKF和CEKF的SLAM.

5.1 仿真

在仿真中, 我们采用一种流行的创建方案[18]用来随机生成仿真环境, 如图3所示. 有35个路标放置在规划好的路径周围, 使用一个最大测量距离为30m, 频率为10Hz的180°范围测量传感器来测量这些路标. 测量噪声被设为均值为0, 标准差分别为0.1m和1°. 车辆以v=3m/s的恒定速度运行, 且最大转向角速度为w=30°/s,取样频率为40Hz. 测量的标准差分别为0.3m/s和3°. 运动和观测模型可以在文献[18]中找到详细描述.

车辆从位置[0,0]出发, 并沿着这条路径循环5次. 使用均方根误差(Root Mean Square Error, RMSE)和平均归一化估计的误差(Normalized Estimation Squared, NEES)来验证全取样和局部取样策略的等价性. 因此, 对每个算法进行50次蒙特卡罗测试. 公平起见, 对每个不同的算法使用相同的随机数种子.

因为标准滤波器和收缩滤波器具有相同的准确度和一致性, 因此基于CEKF和S-UKF的估计在图3中并未给出. 图3显示了关于EKF、UKF和局部取样UKF(Partial Unscented Kalman Filter, PUKF)的实验结果. 图4呈现了从50次蒙特卡罗测试中得到的车辆位姿误差的平均NEES. 从以上两幅图中我们可以发现UKF和PUKF具有完全相同的准确性和一致性, 这可以通过分析表1种的RMES来进一步验证. 根据表中的结果, 与EKF相比UKF和PUKF更具优势. 从不同算法的运行时间来看, 我们能够发现相对于标准的UKF, 局部取样策略能够降低38.98%的复杂度. 此外, S-UKF的复杂度降低了64.33%, 这已经接近CKF的复杂度, 完全能满足SLAM的实时性要求.

图3 对EKF、UKF和PUKF测试的结果. 值得注意的是, UKF和PUKF的结果重合在一起. 星号和点线分别表示真实的路标和路径. 圆和实线分别表示基于UKF和PUKF的对路标和路径的估计. 方形和虚线则表示EKF的结果.

图4 50次蒙特卡罗测试中得到的车辆位姿误差的平均NEES. 实线(顶部)表示EKF. 虚线和点实线分别表示UKF和PUKF, 可以看出他们是完全相同且重叠在一起的.

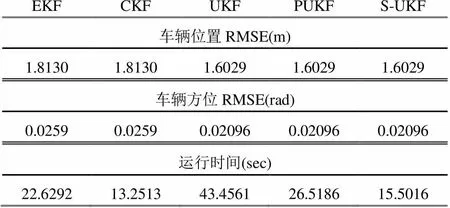
表1 仿真结果

5.2 真实环境数据集实验

为了进一步验证该方法的性能, 我们使用标准数据集-维多利亚公园数据集来进行实验. 该数据集是由一辆带有范围测量传感器和动态GPS天线的移动车辆收集的. 因为树木的遮挡使得GPS测量的数据不连续, 所以该实验并未使用GPS数据. 车辆的运动是由速度和角度编码器来进行测量的. 因为全取样和局部取样策略的等价性已经在上一节验证过, 所以这里只讨论不同方法的效率差异.

图5给出了CEKF和S-UKF在维多利亚公园数据集上的实验结果. 图6显示了EKF、CEKF、UKF、PUKF和S-UKF的累计运行时间. 由图6可以看出, UKF因为复杂度为故其运行时间快速增长至1910.23s. 通过局部取样策略, PUKF的复杂度降低到, 这已经接近EKF的复杂度了. 最后, S-UKF和CEKF在每个阶段的计算成本是大致恒定的. S-UKF的总花费时间是176.32s, 略大于CEKF的157.27s. 此次试验中, 运行了44min, 有204个路标被检测到. 从该实际数据集的实验结果中我们可以知道, 基于S-UKF的SALM可以满足实时性的要求.

图5 使用CEKF和S-UKF的实验结果. 因为GPS信号经常被树木阻挡, 很难提供可靠的地面实况. GPS结果用点表示. 实线和加号分别表示CEKF估计的轨迹和路标. 相应地, 虚线和圆圈表示S-UKF的结果.

图6 不同方法的累计运行时间

6 结语

在本文中, 我们研究了两种降低UKF复杂度的方法, 分别是局部取样策略和收缩方法. 证明了局部取样策略和原有估计的一致性. 在高斯假设下, 相关性的传播被改写为一个类似线性的形式, 这使得收缩方法能适用于UKF中. 进一步的, 基于S-UKF的SLAM能够降低至关于局部路标数目平方的复杂度. 基于仿真和真实环境数据集的实验结果, 证明了该方法可以满足实际应用中的实时性要求.

1 Durrant-Whyte H, Bailey T. Simultaneous localization and mapping: Part i. IEEE Robotics and Automation Magazine, 2006, 13(2): 99–110.

2 Dissanayake MWMG, Newman P, Clark S, Durrant-Whyte HF, Csorba M. A solution to the simultaneous localization and map building (SLAM) problem. IEEE Trans. on Robotics and Automation, 2001, 17(3): 229–241.

3 Thrun S, et al. Simultaneous localization and mapping with sparse extended information filters. The International Journal of Robotics Research, 2004, 23(7-8): 693–716.

4 Davison AJ, Reid ID, Molton ND, Stasse O. MonoSLAM: Real-time single camera SLAM. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2007, 29(6): 1052–1067.

5 Ribas D, Ridao P, Tardos JD, Neira J. Underwater SLAM in manmade structured environments. Journal of Field Robotics, 2008, 25(1112): 898–921.

6 Thrun S, Burgard W, Fox D. A probabilistic approach to concurrent mapping and localization for mobile robots. Autonomous Robots, 1998, 5(3-4): 253–271.

7 Dissanayake MG, Newman P, Clark S, Durrant-Whyte HF, Csorba M. A solution to the simultaneous localization and map building (slam) problem. IEEE Trans. on Robotics and Automation, 2001,17(3): 229–241.

8 Guivant JE, Nebot EM. Optimization of the simultaneous localization and map-building algorithm for real-time implementation. IEEE Trans. on Robotics and Automation, 2001, 17(3): 242–257.

9 Julier SJ, Uhlmann JK, Durrant-Whyte HF. A new approach for filtering nonlinear systems. Proc. of the 1995 American Control Conference. Seattle, WA. 1995. 1628–1632.

10 Montemerlo M. Fastslam: A factored solution to the simultaneous localization and mapping problem. Proc. the AAAI Intrenational Conference on Artificial Intelligence. Edmonton, Canada. 2002. 593–598.

11 Eustice R, Walter M, Leonard J. Sparse extended information filters: Insights into sparsification. 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems. 2005. 3281–3288.

12 Holmes S, Klein G, Murray DW. A square root unscented Kalman filter for visual monoslam. IEEE International Conference on Robotics and Automation (ICRA). Pasadena, CA. 2008. 3710–3716.

13 Andrade-Cetto J, Vidal-Calleja T, Sanfeliu A. Unscented transformation of vehicle states in slam. IEEE International Conference on Robotics and Automation. Barcelona, Spain. 2005. 323–328.

14 Huang GP, Mourikis AI, Roumeliotis SI. A quadratic complexity observability-constrained unscented Kalman filter for slam. IEEE Trans. on Robotics, 2013, 29(5): 1226–1243.

15 Julier SJ, Uhlmann JK. Unscented filtering and nonlinear estimation. Proc. of the IEEE, 2004, 92(3): 401–422.

16 Carlevaris-Bianco N, Eustice RM. Generic factor-based node marginalization and edge sparsification for pose-graph slam. IEEE International Conference on Robotics and Automation (ICRA). Karlsruhe, Germany. 2013. 5748–5755.

17 Lefebvre T, Bruyninckx H, De Schuller J. Comment on “a new method for the nonlinear transformation of means and covariances in filters and estimators”. IEEE Trans. Automatic Control, 2002, 47(8): 1406–1409.

18 Bailey T, Nieto J, Guivant J St. Consistency of the ekf-slam algorithm. IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Beijing, China. 2006. 3562–3568.

Improved Solution Based on Unscented Kalman Filter in the SLAM

WU Yong, GUAN Sheng-Xiao

(School of Information Science and Technology, University of Science and Technology of China, Hefei 230027, China)

A partial sampling strategy was recently proposed to make the computational complexity of the unscented Kalman filter (UKF) quadratic with the state-vector dimension. However, the quadratic complexity remains a thorny issue in the large SLAM. To solve this problem, this paper presents a filtering solution for the SLAM problem called shrink unscented Kalman filter (S-UKF). It firstly proves that equivalence of the whole and partial sampling strategy for the decoupled nonlinear systems. Then a shrink form is presented by reconstruction the cross-correlation items to reduce the computational complexity. Finally, the simulation results and experimental results based on real environmental data sets validate the effectiveness of this method.

SLAM; unscented Kalman filter (UKF); partial sampling; computational complexity

2016-06-18;

2016-08-08

[10.15888/j.cnki.csa.005674]