基于奇异值分解的数字图像压缩技术研究
张晓锋,贾晓强
(1.渭南职业技术学院 机电工程学院,陕西 渭南714000;2.渭南师范学院 网络安全与信息化学院,陕西 渭南 714099)
基于奇异值分解的数字图像压缩技术研究
张晓锋1,贾晓强2
(1.渭南职业技术学院 机电工程学院,陕西 渭南714000;2.渭南师范学院 网络安全与信息化学院,陕西 渭南 714099)
为了实现图像压缩,在分析图像压缩原理的基础上,提出了一种矩阵奇异值分解(SVD)的图像压缩算法,该算法通过对数字图像矩阵进行奇异值分解,将一幅图像转换成包含几个非零值的奇异值矩阵,从而实现了图像压缩。通过Matlab仿真实验,在奇异值从0变化到240的过程中,当奇异值大于50时,随着奇异值的增大,压缩比越来越小,图像慢慢变清晰。和原始图像相比,采用矩阵的奇异值分解压缩方法可以将原始图像压缩20%左右,具有较好的压缩性能。
压缩率;图像压缩;奇异值分解
Abstract:In order to realize the image compression,on the basis of analyzing image compression principle,a matrix singular value decomposition(SVD) image compression algorithm has been proposed.Based ondigital image matrix singular value decomposition was made in the algorithm,an image was converted into singular value matrix containing several nonzero value,and the image compression can be realized.Bymatlab simulation experiment, the singular value varying from 0 to 240, When the singularvalues is greaterthan50,with the increase of singular value the compression ratio is smaller and smaller, and the image become more and more clear.Compared with the original image, using the singular value decomposition of matrix compression method,the original image can be compressed by about 20%,which has good compression performance.
Key words:compression ratio;image compression; singular value decomposition
在信息爆炸的时代,人类日常的工作、生活中多媒体信息越来越多。多媒体信息主要有3种形式:文本、声音和图像(静态和动态)。从信息传播的发展史(电报、电话、传真、广播、电视、网络等)可以看到,传播信息的焦点从声音传给图像。然而,图像是3种形式的信息中占用空间较大的数据,这给图象传输效率以及图象保存带来了很大的困难。对于比较大的图象数据,如果不经过压缩处理,很大程度超出了计算机的存储和处理能力。而且在现有的通信信道的传输速率下,是很难实现多媒体讯息传输的实时性,数字图象需要快速的传输效率和极大的空间储备已经成为推广数字图像的最大障碍。
1 图像压缩基本原理
图像数据之所以能被压缩,就是因为数据中存在着冗余。图像数据的冗余主要表现为:图像中相邻像素间的相关性引起的空间冗余;图像序列中不同帧之间存在相关性引起的时间冗余;不同彩色平面或频谱带的相关性引起的频谱冗余。数据压缩的目的就是通过去除这些数据冗余来减少表示数据所需的比特数。
图像压缩可以是有损数据压缩也可以是无损数据压缩。对于如绘制的技术图、图表或者漫画优先使用无损压缩,这是因为有损压缩方法,尤其是在低的位速条件下将会带来压缩失真。如医疗图像或者用于存档的扫描图像等这些有价值的内容的压缩也尽量选择无损压缩方法。有损方法非常适合于自然的图像,例如一些应用中图像的微小损失是可以接受的(有时是无法感知的),这样就可以大幅度地减小位速。
2 基于矩阵奇异值分解理论下的算法构造
2.1 奇异值分解的图像压缩原理
在图像处理中应用SVD(奇异值分解)的主要理论背景是:1)图像奇异值的稳定性非常好,即当图像被施加小的扰动时,图像的奇异值不会有大的变化;2)奇异值所表现的是图像内蕴特性而非视觉特性[4]。
奇异值分解: 对于矩阵,A∈Rm×nr,r>0 其中 m 和n是任意正整数(不约定大小),有下面的分解定理。
1)(奇异值分解)[5]给定 A∈Rm×nr,r>0,则存在正交矩阵 V∈o(m)和 V∈o(m),使得

其中D∈Rm×n是矩形对角矩阵

且 σ1≥σ2,…,≥σn>0.
假设用 n×n维矩阵 A表示要传送的原始图像。假定对矩阵A进行奇异值分解,便得到:

由于ATA∈Rm×n是半正定对称矩阵,且 rank(ATA)=rank(AAT)=rank(A),所以 ATA 的所有特征值是非负的,且有r个正的。因此可以将ATA的n个特征值按降序排列记对应的正交特征向量为 x1,x2,…,xn,且记:
D1=diag(σ1,σ2,…,σn),则有
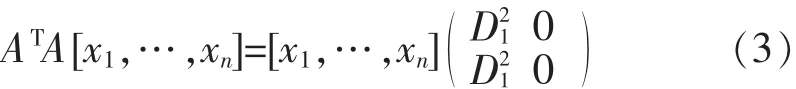
记,V1=[x1,…,xn],V2=[x1,…,xn]则,ATAV1=V1D1由此得到
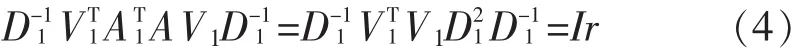
记 U1=AV1D-11∈Rm×n,则由式(4),有 UT1U1=Ir,即是U1的列式互相正交的,因为Rm中任意一组正交向量都可以扩展成为整个空间的一组正交基,所以存在 U2∈Rm×(n-r),使得 U=[U1,U2]∈o(m)。 另外由得 AV2=0, 因此,即AV2的列都是零向量。这些子矩阵满足
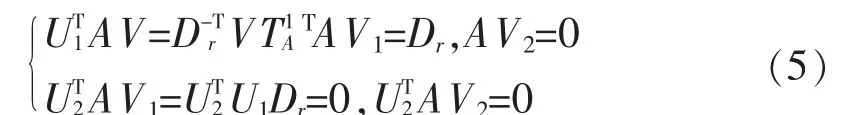
若A∈Rm×n,ATA 对于非零特征值的非负平方根称作A的奇异值,A的奇异值的全体集合记作σ(A)。分解公式(2)称作A的奇异值分解,简记为SVD分解;V的第i列vi=Vri称作A的属于σi的单位右奇异向量;U的第i列ui=Uei称作A的属于σi的单位左奇异向量。
2)(几何 SVD 分解)[6]若 A∈Rm×n,r≠0 则 Rm中存在标准正交基 v1,v2,…,vn,在 Rm中存在标准正交基 u1,…,um,和正实数,使得
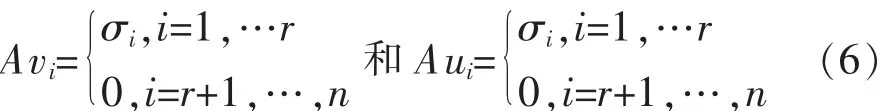
如果把A看成是从向量x∈Rm到Ax∈Rm的线性变换,则可以选择中的基向量,将任何映射表示成矩阵的形式。
在研究将一个空间变换到同一个空间时,矩阵的特征值起到重要的作用,而研究将一个空间映射到不同空间时,特别是不同维数的空间里时,比如超定或欠定方程组所表示的情况下,就需要用矩阵的奇异值来描述算子对空间的作用了。
2.2 奇异值分解进行图像压缩的算法构造
数字图象的定义:一幅图片可以被定义为一个二维函数f(m,n),在这里m和n表示空间坐标,而f对于任何(m,n)坐标的(灰度)的函数值被称为点的灰度值(缩放)。当m,n和f的值都是有限的和离散的,则称这是一个数字图象。由上定义可知,数字图象时可以用三维矩阵来表示的。假定设图像A,将其矩阵化后所得像素为m×n的A数字图像矩阵。对矩阵A进行奇异值分解,由公式(2)有A=UDVT且rank(A)=r,可知对数字图像矩阵A进行矩阵奇异值分解后产生了3个矩阵U、D和V,矩阵A的秩为R。U为m阶矩阵,V为n阶矩阵,D为对角矩阵。D中含有的非零元素组成矩阵[σ1,σ2,…,σN],且 σ1>σ2>…,σN,σ为A的矩阵奇异值。σ的大小反映出了它对应还原到数字图像A的有效作用信息的多少,即σn的值越大其所包含的数字图像A的有效作用信息越多,反之亦然。U和V中同样也包含着能恢复到图像A的所有信息的一部分,正是因为此,若能减少U、D和V 3个矩阵中的一些信息(既是删减矩阵的一些行和列,但这些行和列必须相对应),那么还原到图像时,该还原图像的信息将小于原来的图像信息,则势必能减少其所占的存储空间。即是恢复到图像A′也会比原图像A所占用的存储空间少,从而达到设想的压缩效果。
由于D中每一个奇异值所含有的原来的图像的信息是有限的,在实际操作中可以只取D的前k个奇异值(其后的奇异值假定为零,对恢复图像不起作用),对应着m×m左奇异向量矩阵U的和n×n右奇异向量V的对前K列被选取出来。也就是仅仅使用K个奇异值来近似的表示恢复的矩阵A,即有Ak=Ak所含的内容即为数字图像矩阵A中一部分信息。这种算法的压缩比为:

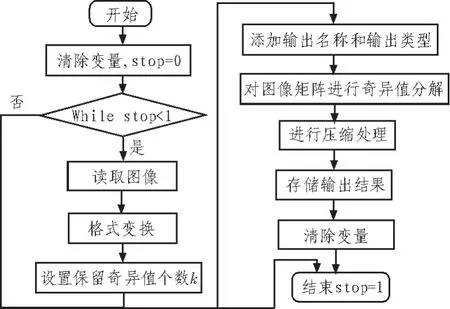
图1 设计流程图
3 仿真分析
3.1 在MATLAB上实现矩阵奇异值分解对预选图像进行压缩
前面的内容介绍到了一些图像压缩的知识和利用矩阵奇异值实现压缩的方法和流程图,下文将结合MATLAB编程语言对预选取的图像实现图像压缩。图2即预选的jpg格式图像。

图2 原图像储存大小=14.4K(b)k=5ρ=21.689储存大小=5.3 K
以下将根据流程图对整个图像进行不同k值(奇异值保留个数)和压缩率的压缩分析:
读入图像girl.jpg,所得的矩阵定为A。由公式(1)以及奇异值的定义可以得到girl.jpg矩阵化后再进行奇异值分解后的奇异值个数为240个。在MATLAB中可使用D=diag(D)函数可以轻易地测量出原图像的所有奇异值,此图的前50个奇异值数值如表1所示。
表1显示出在奇异值按大小排列后,位于前面的奇异值含有能还原图像的信息越多,压缩能力越强。图3将给出压缩能力与奇异值个数的数字关系。
从图3中,体现出了对girl.jpg图像的压缩效果与保留奇异值数目多少不同的关系。从中可以看出,当奇异值k在小于第50个奇异值 (从大到小排列)以后的奇异值对图像的贡献较小。同时也体现出,奇异值k的个数在向左方递减的同时,压缩比值越大,其图像的失真度越高
3.2 结果分析
从表2压缩前后属性对比中可以从视觉上感官出保留的奇异值k的个数多少对重建图像的影响,通过表2的各项参数分析表明,当k=5压缩为5.3 kB,k=15为 9.6 kB,k=20为 11.2 kB,k=30为 12.3 kB,k=40为12.8 kB。可以看出,k值越小,压缩后的图像越明显,但是图像不清晰,随着k值的变大,图像慢慢变清晰,但压缩率变小,满足奇异值的曲线分布。
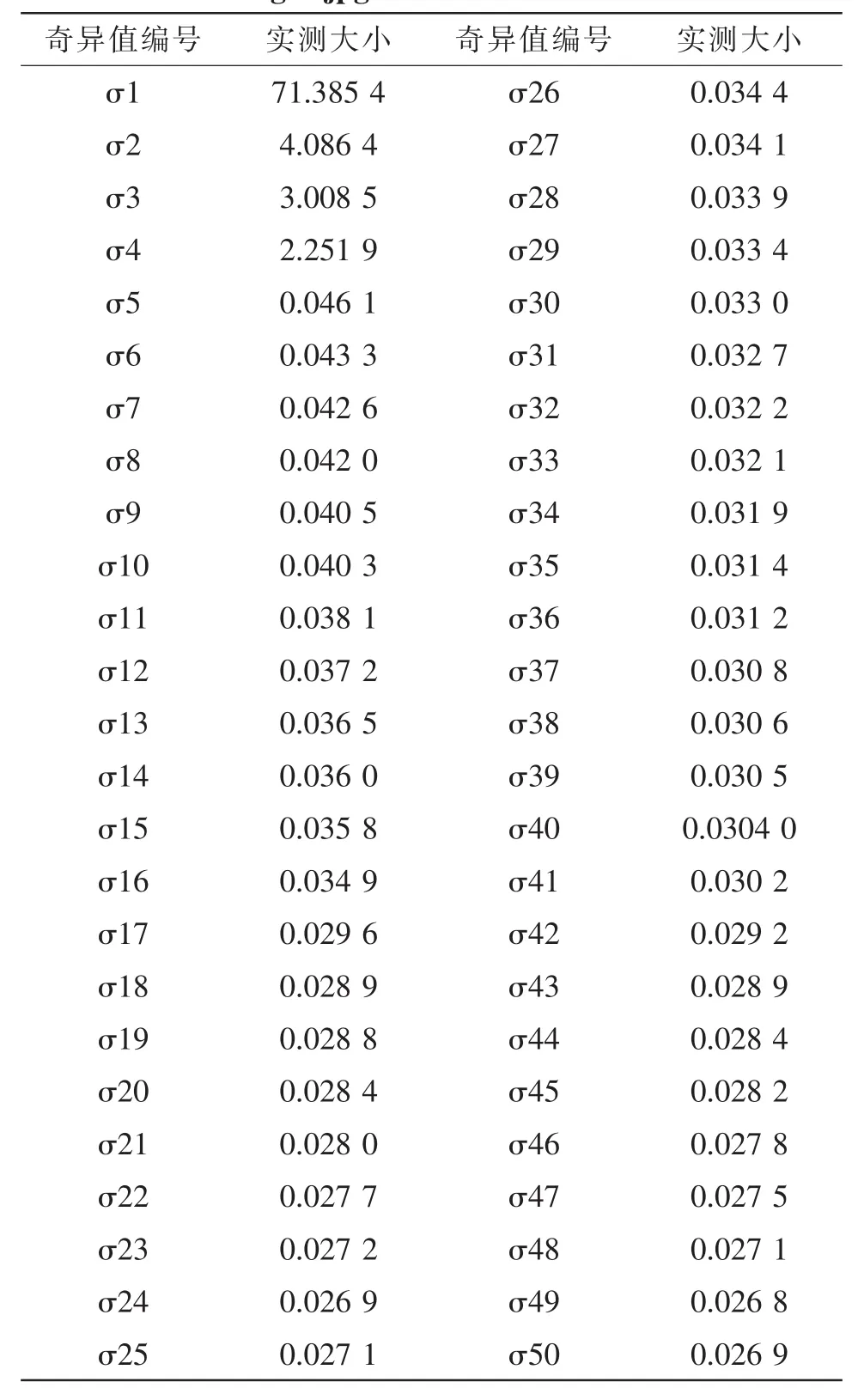
表1 girl.jpg前50个奇异值一览表

图3 压缩比与奇异值个数关系曲线图
4 结 论
用奇异值分解法来实现图像压缩,在不影响图像质量前提下,利用计算机模拟,分析实验数据结果表明,重构效果较好,运行时间较短,速度快,储存空间减少。使图象压缩具有更高的效率和精度。在选择矩阵的奇异值分解来实现图像的压缩与恢复时,可以达到很高的压缩比同时不产生图像失真。当然,利用奇异值进行压缩的时候,由于这些特征值都是由该矩阵自身和它的转置的乘积所求出的,计算量是比较大的。

图 4 (中)k=30 ρ=4.563储存大小=12.3 K

图 5 k=40(右)ρ=3.422储存大小=12.8 K
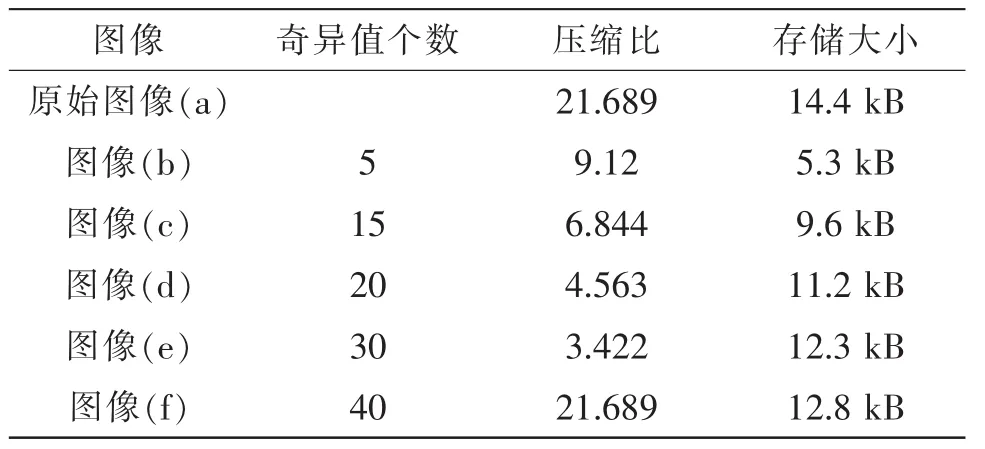
表2 压缩前后属性对比表
[1]刘直芳,王运辉.数字图像处理与分析[M].北京:清华大学出版社,2015.
[2]韦仙,康睿丹.基于降维压缩法的图像重构[J].武汉工程大学报,2015,37(12):69-74.
[3]张成楠.基于奇异值分解图像压缩算法的研究[J].山西电子技术,2010,4(2):79-80.
[4]陈一虎.基于SVD图像压缩技术研究[J].价值工程,2011,13(2):169-170.
[5]罗小桂.矩阵奇异值分解(SVD)的应用[J].井冈山医专学报,2013,12(4):133-135.
[6]王建辉.图像矩阵降维压缩的一种新方法[J].控制与决策,2007,22(12):1408-1416.
[7]吴俊政.一种基于奇异值分解的图像压缩方法[J].计算机与数字工程,2009,37(5):136-139.
[8](美)冈萨雷斯等.数字图像处理[M].北京:电子工业出版社,2009.
[9]陈波,王红霞,成礼智.图像压缩中的快速方向离散余弦变换[J].北京:软件学报,2011,22(4):826-832.
[10]张军,成礼智,杨海滨,等.基于纹理的自适应提升小波变换图像压缩 [J].计算机学报,2010,33(1):185-192.
[11]黄长春,徐抒岩,胡君.奇异值分解遥感图像压缩算法研究[J].计算机仿真,2011,28(8):226-353.
[12]张飞艳,谢伟,陈荣元,等.基于视觉加权的奇异值分解压缩图像质量评价测度[J].电子与信息学报,2010,32(5):1062-1065.
[13]王怀光,张培林,张云强,等.基于奇异值分解和小波变换的图像压缩算法[J].火炮发射与控制学报,2012,12(15):38-42.
[14]王郗雨,杨晓梅,胡学姝.基于奇异值分解的压缩感知核磁共振图像重构算法 [J].计算机应用研究,2013,30(4):1248-1252.
[15]赵峰,黄庆明,高文.一种基于奇异值分解的图像匹配算法[J].计算机研究与发展,2010,47(1):23-32.
Research on digital image compression technology based on singular value decomposition
ZHANG Xiao-feng1,JIA Xiao-qiang2
(1.Department of Computing Science, Weinan Vocational and Technical College,Weinan714000,China;2.School of Network Security and Information,Weinan Normal University,Weinan714099,China)
TN911
A
1674-6236(2017)19-0179-04
2016-09-04稿件编号201609028
陕西省重点扶持学科基金资助项目(14XZD010);渭南师范学院科研基金资助项目(16YKS004)
张晓峰(1981—),男,陕西渭南人,硕士,讲师。研究方向:WEB工程,数字图像处理。

