基于等距线阵的四种DOA估计算法性能分析
马怡
(河海大学 计算机与信息学院,江苏 南京 211100)
基于等距线阵的四种DOA估计算法性能分析
马怡
(河海大学 计算机与信息学院,江苏 南京 211100)
阵列信号处理技术在远场信号DOA的估计方面的研究成为热点。本文就四种经典的DOA估计算法:MUSIC算法、ESPRIT算法、TLS-ESPRIT算法和Toeplitz矩阵重构算法进行对比研究,目的是为工程实现算法的选择提供了一个参考的理论依据。就笔者所知,对这4种算法性能比较分析的公开报道较少。通过MATLAB软件仿真的方法,分析了各算法的优缺点,并总结出各算法适用范围和其理论依据。
DOA估计;MUSIC算法;ESPRIT算法;Toeplitz算法
Abstract:The research of array signal processing technology in the estimation of the far field signal DOA has become a hot spot.To provide a reference to the theoretical basis for the engineering implementation algorithm selection,we compare the four classical DOA algorithms in this paper:MUSIC algorithm,ESPRIT algorithm ,TLS-ESPRIT algorithm and Toeplitz matrix reconstruction algorithm.Just as I know,the comparison and analysis of the performance of the four algorithms are rarely publicly reported.Through the MATLAB software methods,we analyzed the advantages and disadvantages of each algorithm,and then summarized the applicable range of each algorithm and its theoretical basis.
Key words:DOA estimation;MUSIC algorithm;ESPRIT algorithm;Toeplitz algorithm
阵列信号处理是信号处理技术领域内的一个重要分支。运用阵列信号处理技术来实现波达方向(DOA)估计的研究在近年取得了丰硕的成果。DOA估计的基本问题是确定多个信号到达阵列参考阵元的方向角。
常规波束形成算法(CBF法)[1]是公认的较早的DOA估计方法。20世纪70年代之后,多种DOA估计算法兴起,如最大似然(ML)算法[2]、子空间拟合(SF)算法[3]等。同属特征结构的子空间方法[4]的算法也有很多,其中最著名的是MUSIC方法和ESPRIT方法。 MUSIC(multiple signal classification)算法是Schmidt在1979年提出的,于1986年重新发表[5]。ESPRIT (estimating signal parameters via rotationalinvariance techniques)算法是由Roy等人于1986年提出的[6-7]。
ESPRIT算法和MUSIC算法对相干信源DOA估计的思想方法各不相同。MUSIC算法的基本思想是利用信号子空间和噪声子空间这两个互补空间之间的正交特性估计空间信号的方位。而ESPRIT算法的基本思想是通过空间旋转将向量x(n)经过旋转后变成向量y(n),保持两个向量对应的信号子空间的不变性,后求解旋转不变矩阵,最后得出DOA估计。其中TLS-ESPRIT算法是在ESPRIT算法的基础上改进而来,其算法思想与ESPRIT算法基本一致。
利用ESPRIT算法对相干信源波达方向进行估计的时候会产生阵列孔径损失的问题,因此之后有学者提出可用Toeplitz矩阵重构算法完成相干信源DOA估计[8-9],这是一种非降维类处理算法,类似的方法还有很多[10]。Toeplitz矩阵重构算法的基本思想是首先分别对阵元和参考阵元的接收数据的相关函数进行排列得到Hermitian Toeplitz矩阵,之后再进行奇异值分解,进而得到相干信源的DOA估计。
文中以等距线阵为研究背景,对MUSIC算法、ESPRIT算法、TLS-ESPRIT算法以及Toeplitz矩阵重构算法的性能进行综合对比研究,为工程实现算法的选择提供理论依据。
1 4种算法DOA估计理论实现
1.1 经典MUSIC算法DOA求解
MUSIC算法是一种基于矩阵特征空间分解的方法[11]。从几何角度讲,信号处理的观测空间可以分解为相互正交的信号子空间和噪声子空间。协方差矩阵中与信号对应的特征向量组成信号子空间,所有最小特征值对应的特征向量组成噪声子空间。
具体的MUSIC算法估计步骤如下:
1)根据N个接收信号矢量得到协方差矩阵RXX,并对其进行特征值分解。
2)将得到的特征值按照大小排序,然后分解出信号子空间和噪声子空间,得到噪声矩阵E。
3)根据公式
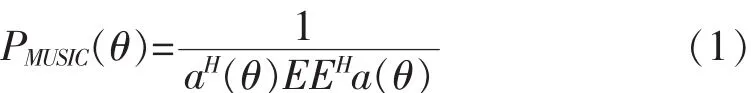
计算谱函数,其中θ是自变量。MUSIC算法是通过寻找峰值来得到相干信源波达方向的估计值。
1.2 ESPRIT算法DOA求解
ESPRIT算法,又可称为LS-ESPRIT算法。这个算法的优点是可以直接通过特征值得到信号参数,而不需要进行繁琐的谱峰搜索过程,思想核心是求旋转矩阵y(n)[12]。在实际应用中,把同一阵列分解成2个子阵列,这两个子阵列的阵元数目完全相同,两个子阵列仅相差一个旋转矩阵。
ESPRIT算法有两种估计方法,本次实验设计采用后向平移的ESPRIT算法。
具体的ESPRIT算法实现步骤如下:
1)由两个子阵的接收数据分别得到两个子阵的数据协方差矩阵xx。将矩阵进行特征值分解

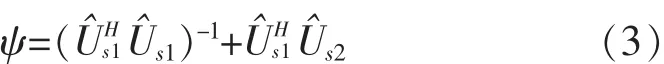
并将ψ进行特征值分解得到N个特征值,就可得到对应的N个信号的波达方向。
1.3 TLS-ESPRIT算法DOA求解
基本ESPRIT算法可以看成是一种最小二乘算子。现已广泛认识到,奇异值分解(SVD)[13]和总体最小二乘(TLS)的应用可以解决在求解广义特征值问题的时候,最小二乘算子导致的一些问题。
TLS-ESPRIT算法求解步骤如下:
2)由分解得到的Us构造矩Us12阵,并按照式

进行特征值分解得到矩阵E。

然后按照公式(5)将矩阵分为4个小矩阵。
3)按照式:

得到ψTLS并对其特征值分解,得到N个特征值,就可以得到对于N个信号的波达方向。
不吃就别给孩子吃,吃是人的本能,饿了自然会吃。小宝宝不爱吃米饭也没关系,面条、馒头、面包都可以,只要吃就行。不吃主食光吃菜问题也不大,吃完再来点小饼干即可。
1.4 Toeplitz矩阵重构算法DOA估计
通过构建Toeplitz矩阵,其基本思想是将接收相干信源的协方差矩阵恢复为满秩矩阵,然后去相干。该算法较之于TLS-ESPRIT等算法的优势在于不需要损失阵列孔径,但是仍然需要进行特征值的分解。
由式
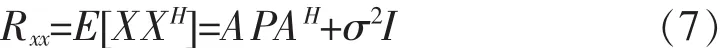
可知协方差矩阵Rxx具有Toeplitz性质,它的秩不受信号相干性的干扰[14]。该算法首先对各个阵元的接收数据和第一个阵元的接收数据的相干函数进行排列,得到Hermitian Toeplitz矩阵,通过奇异值分解可以得到信号子空间和噪声子空间,从而实现DOA估计。
具体步骤如下:
1)由协方差矩阵RXX得信号子空间和特征值。
2)按式:

构造矩阵B,抽取矩阵B的前m-1行构造矩阵B1,抽取后m-1行构造矩阵B2。
3)按式

4)得到矩阵D后进行特征值分解,由特征值就可以得到对应的N个信号的到达角。
2 仿真实现及结果分析
2.1 4种算法运行所需时间
当输入2个信号,阵元数分别为10时,snr=0,d=λ/2,入射角度为 30°和 60°,快拍数设置为 512,将4种算法计算相干信源波达方向所需的时间进行比较,如表1所示。

表1 不同算法的运行时间
可见虽然MUSIC算法比较精确,但是因为需要进行谱峰搜索的繁杂过程,所以运算所需时间是4种算法中最长的。TLS-ESPRIT算法所需时间最少。
2.2 阵元数对4种算法估计精度的影响
输入单信号源,入射角度为分别为50°时,快拍数同样设置为 512,阵元间距 d=λ/2,信噪比snr=0。对在不同阵元数情况下,4种算法的估计均方根误差进行比较,进行100次试验后结果如图1所示。
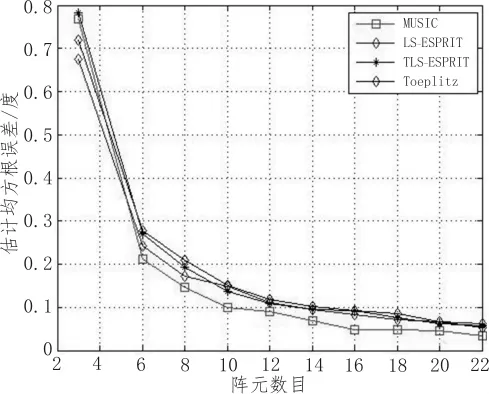
图1 不同阵元数情况下均方根误差
因为阵元数必须大于2,才能正确的描述波达方向。同时将阵元间距设置为2,因为阵元等间距,DOA估计越精确[15]。从图中可以看出,阵元数越多,四种算法估计结果越精确,且误差大小皆趋于稳定。从图中同样可以看出,在阵元间距小于4的时候,计算结果偏差较为严重,不能作为参考数值。很明显,MUSIC算法的计算结果最为精确,误差一直是最小的。
2.3 信噪比对4种算法估计精度的影响
输入单信号源,d=λ/2,入射角度为 50°,阵元数设为10,快拍数为512,实验100次时,不同信噪比情况下,4种算法的估计均方根误差进行比较,结果如图2所示。
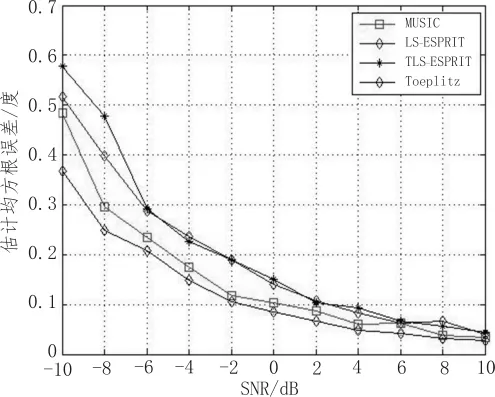
图2 不同信噪比情况下均方根误差
此次仿真考虑信噪比SNR分别为-10 dB至10 dB,将各个算法算出的DOA估计均方根误差进行比较分析,可知总体上随着信噪比的增大,估计误差越来越小,即估计精度越来越高。对-10 dB和10 dB之间离散化取值,可见在-10 dB的时候,4种算法的估计误差差距较大。在-10 dB和10 dB之间,虽然4种算法的误差都是越来越小,但是仍然可以清晰的看出4种算法估计误差的精确程度。在10 dB的时候,4种算法的估计误差很小。Toeplitz矩阵重构算法的估计误差相较于其他两种算法的误差更小,估计结果更精确。MUSIC算法次之,而ESPRIT算法和TLS-ESPRIT算法的估计误差一直不相上下。
2.4 快拍数对算法估计精度的影响
当输入 2信号源,阵元数为 10,snr=0,d=λ/2时,入射角度为30°和60°时,进行100次实验,快拍数对Toeplitz矩阵重构算法对DOA的估计误差的影响如图3所示。
设置快拍数等间距为20,是为了估计结果更精确。图中表明,快拍数对算法估计结果的影响也很明显。当快拍数较少时,估计误差明显较大,估计结果越不精确,已经失去了数值的参考价值。快拍数越大,估计误差越小,精度越高。快拍数增大到一定程度之后,估计误差趋于稳定。可见快拍数亦是算法对相干信源DOA估计精确程度的一个不可忽略的重要因素。
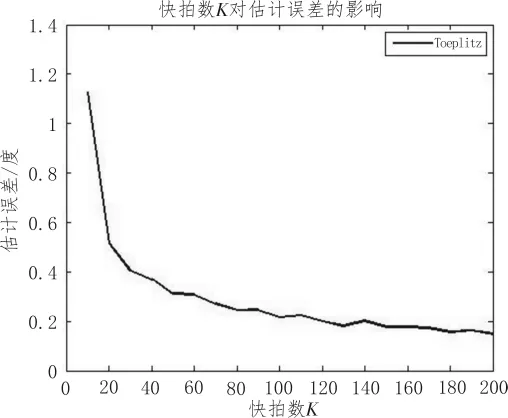
图3 不同快拍数情况下估计误差
3 结 论
本文分别从阵元数、信噪比和快拍数等方面比较分析了MUSIC算法,ESPRIT算法,TLS-ESPRIT算法以及Toeplitz矩阵重构算法各自的优缺点。理论分析和仿真研究表明,MUSIC算法适用于高分辨谱估计,缺点是需要特征值分解以及繁杂的谱搜索过程,所以计算时间最长速度最慢,由此如果芯片的处理速度较快,精度要求较高的时候可以考虑MUSIC算法。ESPRIT算法适用于较高分辨率的谱估计,较之于MUSIC算法而言不需要谱搜索的过程,计算速度得到提高,但是仍需要进行特征值分解步骤,所以适用于芯片处理速度较慢,精度要求高的情况。TLSESPRIT算法是在ESPRIT算法的基础上改进得到的算法,解决了最小二乘法在求解广义特征值问题上潜在的数值困难,且计算时间比ESPRIT算法快,所以适用于芯片处理速度慢,精度要求高的情况。而Toeplitz矩阵重构算法有很好的研究前景,其优势在于不需要损失阵列孔径,并且算法的分辨性能更优越,有更好的实用性,所以应用的范围也就更广泛。
[1]Krim H,Viberg M.Two decades of array signal processing research[J].IEEE Signal Processing Magazine,1996,13(4):67-94.
[2]Stoica P, Nehorai A.MUSIC, maximum likelihood,and cramerrao bound[J].IEEE Transcations on Acoustics Speech and SignalProcessing,1989,37(5):720-741.
[3]Viberg M,Ottersten B,Kailath T.Detection and estimation in sensor arrays using weighted subspace fitting[J].IEEE Transactions on Acoustics Speech and Signal Processing,1991,39(11):2436-2449.
[4]Uttam Shikhar,Goodman N A.Superresolution of coherent sources in real-beam data[J].IEEE Transcations on Aerospace and Electronic Systems,2010,46(3):1557-1566.
[5]Serpedin E,Giannakis G B.Blind channel identification and equalizations with modulation-induced cycl-ostationarity.IEEE Trans.Signal Processing,1998,46:1930-1944.
[6]Roy R,Paulraj A,Kailath T.ESPRIT-a subspace rotation approach to estimation of parameters of cissoids in noise[J].IEEE Transactions on Acoustics Speech and Signal Processing, 1986,34(10):1340-1342.
[7]Roy R,Kailath T.ESPRIT-estimation of signal parameters via rotational invariance techniques[J].IEEE Transactions on Acoustics Speech and Signal Processing, 1989,37(7):984-995.
[8]唐玲,宋弘,陈明举,等.一种基于Toeplitz矩阵重构的相干信源DOA估计算法[J].电子信息对抗技术,2010,25(3):9-11,30.
[9]Li D,Dong C,Huang J.A study on the application of Toeplitz approximation method on DOA estimation [C].Proceedingsofthe2010 2nd InternationalConference on SignalProcessing Systems(ICSPS),2010,3:215-218.
[10]梁浩,李晓波,王磊.采用单次快拍数实现信源DOA估计[J].数据采集与处理,2013,28(1):58-63.
[11]王永良,陈辉,彭应宁,等.空间谱估计与算法[M].北京:清华大学出版社,2004.
[12]刘艳,杨力生,黄卫华.ESPRIT算法估计性能分析[J].信息技术,2011(3):100-102.
[13]云彩霞,李珊,白彦霞.基于改进ESPRIT算法的波达方向估计[J].现代电子技术,2010,33(1):61-63.
[14]张小飞,汪飞,徐大专.阵列信号处理的理论和应用[M].北京:国防工业出版社,2010.
[15]司元雷.均匀阵列下TLS-ESPRIT改进算法研究[J].无线通信技术,2015,24(3):30-33.
Performance analysis of four kinds of DOA estimation algorithms based on uniform linear array
MA Yi
(College of Computer and Information,Hohai University, Nanjing211100,China)
TN911.7
A
1674-6236(2017)19-0127-04
2016-08-15稿件编号201608105
马 怡(1993—),女,江苏常州人,硕士研究生。研究方向:阵列信号处理。
——以鲁甸地震相关新浪微博为例

