基于对数障碍法的网络流量管理算法
张 洪, 王俊杰, 李牧泽, 胡 英, 刘 山, 冯大峰, 何 珠
(1.成都大学 信息科学与工程学院, 四川 成都 610106;
2.成都大学 模式识别与智能信息处理四川省高校重点实验室, 四川 成都 610106;3.四川大学 出国留学预备学院, 四川 成都 610065;4.成都大学 旅游与经济管理学院, 四川 成都 610106)
基于对数障碍法的网络流量管理算法
张 洪1,2, 王俊杰1, 李牧泽3, 胡 英4, 刘 山1, 冯大峰1, 何 珠1
(1.成都大学 信息科学与工程学院, 四川 成都 610106;
2.成都大学 模式识别与智能信息处理四川省高校重点实验室, 四川 成都 610106;3.四川大学 出国留学预备学院, 四川 成都 610065;4.成都大学 旅游与经济管理学院, 四川 成都 610106)
为了有效描述和管理计算机网络流量问题,提出一种基于对数障碍法和节点队列的新算法.首先利用对数障碍函数分析影响网络流量的关键因素,然后利用对数障碍法和节点队列拥塞情况动态调节网络分布式发包速率,从而使网络获得最大的聚合效用.仿真实验结果显示,算法具有较好的适应性.
网络流量;对数障碍法;拥塞
0 引 言
随着现代网络技术的快速发展,网络拥塞已是一个不可避免的问题,网络拥塞会导致信息传输时间的显著增加和网络整体性能的下降.相关研究发现,网络节点产生大量数据流,而并发数据流是导致网络产生拥塞的主要原因.此外,网络本身的一些属性甚至会对网络拥塞的产生与传播起到助长的作用,例如节点的容量、节点处理数据包的速度、通信链路的带宽以及网络的拓扑结构等等.对此,如何进行准确的流量预测与合理的流量管理已成为现实网络中一个亟待解决的问题.
目前,在流量预测与管理上,研究者们普遍专注于对网络最大流的研究,并取得了系列成果[1-7].其中,魏娟等[6]基于离散消失排队和三维元胞自动机提出了一种新的计算方法QCA,该算法具有较好的适应性,但网络稳定性还有待提升;赵姝等[7]通过构造原有网络的层次,计算各相邻节点之间的最大流,然后获得整个网络最大流估算,为大规模网络中快速计算最大流的求解提出解决方法,实验也表明该算法能够把近似误差控制在1%左右,但由于该算法实现较为复杂,运行时间会稍有增加.在此基础上,本研究利用对数障碍函数法和基于节点队列长度提出一种新的网络流量管理算法(logarithmic barrier and queuing method,LBQM),并通过仿真实验对比研究该算法和其他算法的性能差异,以期获得网络效用最大化.
1 基于对数障碍函数的网络效用最大化
单径路由在当今的互联网被广泛应用,然而单径路由将会限制系统的吞吐量.如果将数据流进行灵活的分割,然后通过多条路径发送,预期可以获得更高的有效性和稳健性.对于多径路由,可用矩阵H的列来表示所有可用的路径,这样,多径网络效用最大化问题可以表示为,
subjecttoHx≤c
(1)
这是一个带线性约束的凸优化.对于式(1),因为源在包损失后只能减小其速率,从而对贪心流的收敛性很差.此外,因为效用仅是基于吞吐量的,一些链路几乎是满容量运行,从而导致大的延迟,对于突发流量问题尤其突出,通过对偶分解可以得出其分布式解决方案,即考虑凸优化问题,
subjecttoHx+r=c
(2)
其中,f是凸的、非减的二次可微函数,ω是效用和成本之间的权衡参数.当链路负载增加时,f给出更严重的约束,比如ey1/c1.通过对数障碍函数可以对式(2)进一步优化,以提高其最优性和改善收敛性.
subjecttoHx+r=c
(3)
其中,ωl是与约束rl≥0,即yl≤cl,相联系的障碍参数.然而,如果直接求解式(3),则因为目标函数不是严格凹函数,从而对偶函数是不可微的,这种情况很难得到稳定的速率控制算法.对此,本研究在目标函数中引入与速率非负约束xr≥0相联系的对数惩罚项,从而考虑,
subjecttoHx+r≤c
(4)

(5)
其中,

(6)
(7)
从而得到式(4)的对偶问题为,
(8)



subjecttoHx≤c
(9)
的解,且λ*是与之对应的Lagrange乘子.
基于式(8),本研究利用对偶分解得到稳定的分布式速率控制算法——投影梯度法,即,令β>0是常数步长,则对所有l∈L,有,

(10)
其中,对所有l,有,
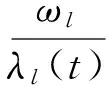
对所有S有,
中西方因历史和社会因素不同,英国偏向直线思维方式,我国则偏向曲线思维,因此中西方人认识事物的出发点不同,语言表达习惯也有所不同,这也是商务英语翻译中易出问题的关键。
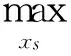
(11)

式(11)表示源S在时刻t根据路径拥塞水平极大化的净效用.
2 基于对数障碍法的流量管理算法
本研究基于对数障碍法的流量管理算法步骤如下:
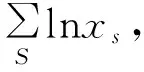
Step2.在式(10)和式(11)中忽略反馈延迟,对r∈s,源S需要对基于Tr更新发送速率,这里Tr是源S收到沿路径r的所有链路的反馈需要时间.
Step3.更新源S的路径r的流速率,对于给定的价格向量λ(t),由式(11)知,xs(t)是每个子问题的解当且仅当,

(12)


Step5.引入加权因子γ来避免在每次迭代中产生巨大的变化.实验中,取γ=0.1.基于以上分析可得出源速率更新为,

(13)

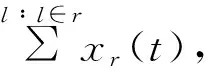

(14)

Step8.重复Step3~Step7,直到网络稳定在最大流量运行.
Step9.算法结束.
3 数学仿真
本研究通过实际仿真环境中本算法与其他经典算法的最大流数据与性能对比来验证算法的有效性.
首先,在NS2中建立网络拓扑结构,并且设置每个数据包大小为256 Byte,到达速率为2 000 Kibit/s,时延20 ms,各条链路容量为20 Mibit/s,各节点缓存容量为2 000 Kibit[6].同时将本研究所提方法与网络单纯形法(Simplex)及最短增载轨算法(distance-directed augmenting path,DDAP)应用到仿真环境中进行对比.在上述参数的设定下网络稳定运行100 s,然后截取后50 s 3种算法获得的网络最大流数据,结果如图1所示.

图1 3种算法仿真实验对比
从图1中可以看出,本研究提出的LBQM算法与实际统计的最大流最为接近,而Simplex算法预测结果误差最大.经过残差分析,LBQM、DDAP和Simplex算法的误差分别为10.32%、15.34%和20.16%.
其次,本研究对3种算法的丢包情况进行了测试,图2给出了90 s仿真时间内3种算法的丢包统计结果.
从图2可以看出,DDAP和Simplex算法的丢包波动较为频繁,而LBQM算法因采用了线性分形稳定运动来降低数据包的突发性,使丢包性能得到了优化.
从图1和图2的结果能够看出,本研究提出的LBQM算法较DDAP和Simplex算法性能有较大提高,具有较好的适应性.

图2 3种算法丢包比较
4 结 论
本研究首先通过对数障碍函数对计算机网络中流量管理问题进行描述,采用适当的流量管理策略可以显著提升网络性能.基于对数障碍法的流量管理算法使用动态调整源发包速率,充分考虑节点底层排队队列情况以及节点拥塞度,使得网络发包总速率可以维持在一个比较稳定的最大流状态.实验表明,本研究提出的算法对改善网络最大流性能有一定的提升,对维护网络的稳定性有较大的帮助.
[1]Goldberg A V,Rao S.Beyondtheflowdecompositionbarrier[J].J ACM,1998,45(5):783-797.
[2]Ford L R,Fulkerson D R.Marimumflowthroughanetwork[J].Can J Math,1956,8(5):359-373.
[3]Dantzig G B.Applicationofthesimplexmethodtoatransportationproblem[C]//ActivityAnalysisandProductionandAllocation.New York,USA:Wiley,1951:359-373.
[4]Dinic E A.Algorithmforsolutionofaproblemofmaximumflowinnetworkswithpowerestimaton[J].Sov Math Dokl,1970,11(8):1277-1280.
[5]Edomonds J,Karp R M.Theoreticalimprovenmentsinalgorithmicefficiencyfornetworksflowproblems[J].J ACM,1972,19(2):248-264.
[6]魏娟,张丽,张洪,等.基于离散消失排队的网络最大流计算方法[J].计算机工程与设计,2016,37(10):2608-2612.
[7]赵姝,苏建忠,刘倩倩,等.分层法求解网络最大流的研究[J].计算机研究与发展,2014,51(8):1845-1853.
Abstract:In order to describe and manage computer network flow effectively,this paper proposes a new method based on the logarithmic barrier and queuing method(logarithmic barrier and queuing method,LBQM).At first,this algorithm uses the logarithmic barrier function to analyze the key factors which influence the network flow,and then utilizes the logarithmic barrier method and the congestion condition of queuing to adjust the packet rate of distributed network dynamically,so that the network obtains the largest aggregation utility.The simulation experimental results show that LBQM has better adaptability.
Keywords:network flow;logarithmic barrier method;congestion
NetworkFlowManagementAlgorithmBasedonLogarithmicBarrierMethod
ZHANGHong1,2,WANGJunjie1,LIMuze3,HUYing4,LIUShan1,FENGDafeng1,HEZhu1
(1.School of Information Science and Engineering, Chengdu University, Chengdu 610106, China;2.Key Laboratory of Pattern Recognition and Intelligent Information Processing, Chengdu University, Chengdu 610106, China;3.College of International Studies Education Ministry, Sichuan University, Chengdu 610065, China;4.School of Tourism, Economics and Management, Chengdu University, Chengdu 610106, China)
TP393.06
A
1004-5422(2017)03-0265-04
2017-06-20.
成都大学校基金(2016XJZ14)、 模式识别与智能信息处理四川省高校重点实验室2017开放课题(2017KFKT12)、 成都大学2016年国家级大学生创新训练计划(CDU-CX-2016013)、 四川省网络智能信息处理实验室开放课题(szjj2017-008)资助项目.
张 洪(1980 — ), 男, 博士, 副教授, 从事计算机网络技术研究.

