Numerical Simulations for the Load Characteristics of Internal Solitary Waves on a Vertical Cylinder

WANG Xu,LIN Zhong-yi,YOU Yun-xiang,YU Rui

(1.State Key Laboratory of Ocean Engineering,Shanghai Jiaotong University,Shanghai 200240,China;2.CAS Key Laboratory for Mechanics in Fluid Solid Coupling Systems,Institute of Mechanics,Beijing 100190,China;3.School of Jiaxing Nanyang Profession and Technology,Jiaxing 314003,China;4.Jiangsu Local Maritime Safety Administration,Nanjing 210004,China)

Numerical Simulations for the Load Characteristics of Internal Solitary Waves on a Vertical Cylinder

WANG Xu1,2,LIN Zhong-yi3,YOU Yun-xiang1,YU Rui4

(1.State Key Laboratory of Ocean Engineering,Shanghai Jiaotong University,Shanghai 200240,China;2.CAS Key Laboratory for Mechanics in Fluid Solid Coupling Systems,Institute of Mechanics,Beijing 100190,China;3.School of Jiaxing Nanyang Profession and Technology,Jiaxing 314003,China;4.Jiangsu Local Maritime Safety Administration,Nanjing 210004,China)

Abstract:According to the applicability conditions for three types of internal solitary wave theories including KdV,eKdV and MCC,a numerical method based on the Navier-Stokes equations in a twolayer fluid was presented to simulate the strongly nonlinear interaction between internal solitary waves and the vertical cylinder,where the velocity-inlet boundary is applied by using of the depth-averaged velocities in the upper-and lower-layer fluids induced by the internal solitary wave.Numerical results show that the waveform and amplitude of the internal solitary waves are in good agreement with the experimental and theoretical results.The horizontal and vertical forces,as well as torques on the vertical cylinder obtained from the numerical method also agree well with experimental results.Besides,the numerical results indicate that the horizontal and vertical forces on the vertical cylinder due to internal solitary waves can be divided into three components,including the wave and viscous pressure-difference forces,as well as the frictional force,where the fractional force is not significant and can be neglected;for the horizontal force,the orders of the magnitudes between the wave and viscous pressure-difference forces are the same,which shows that the effect of the fluid viscosity is significant;for the vertical force,the component of the viscous pressure-difference force is not significant so that the effect of the fluid viscosity can also be neglected.Moreover,the effects of the vertical cylinder on the waveform and flow field induced by the internal solitary wave are small.Therefore,it is feasible to calculate the horizontal and vertical forces on the vertical cylinder due to internal solitary waves by the Morison and Froude-Krylov formulas respectively.

Key words:two-layer fluid;internal solitary waves;numerical simulation;load characteristics

0 Introduction

As a compliant floating structure,Spar platform is well suited for deep water applicationslike drilling,production,processing,storage and off-loading of ocean deposits[1].In practical applications,ocean conditions have great impacts on the safety of Spar,therefore it is necessary to consider hydrodynamic characteristics of the Spar platform under various ocean conditions.

A large number of observations showed that internal solitary waves occur frequently and exist widely in the South China Sea[2],which has resulted in severe impact on the operation of ocean engineering structures[3].With the further exploitation of the oil and gas in South China Sea,internal solitary waves have become one fundamental environmental factor which must be considered.

Nonlinearity and dispersion are two fundamental mechanisms of gravity wave propagation in fluids.As a general rule,it is well known that nonlinearity tends to steepen a given waveform during the course of its evolution,while dispersion has the opposite effect and tends to flatten steep free-surface gradients[4].According to the relative importance of nonlinear and dispersion,internal solitary waves can be generally described as KdV(Korteweg-de Vries)theory,eKdV(extended KdV)theory,MCC(Miyata-Choi-Camassa)theory and others[5-6].In order to quantitatively distinguish the above three theories,Huang[7]summarized the applicability conditions for former three different internal solitary wave models based on a large number of experiments.

Since the vertical cylinder is the main structure form of the spar platform,it has great importance for both theoretical research and engineering application to study the load characteristics of internal solitary waves on it.Although the load and motion response characteristics of deepwater floating structures due to internal solitary waves have been studied preliminarily by far[8-9],most of hydrodynamic mechanism are not yet clear,including the formation mechanism of various load components,the influence mechanism of viscosity factor on internal solitary wave loads,and the applicability of calculating loads of the floating structure by Morison formulas.The CFD(Computational Fluid Dynamics)simulation provides an effective way to deeply analyze the questions mentioned above.However,the previous simulated waveform and amplitude are often unable to be controlled in varying degrees due to the lack of considering the applicability conditions for solitary wave theories[10-11].Thus one of the key problems is how to select an appropriate internal solitary wave theory as the basis for numerical wave-making in the process of studying the strong nonlinear interaction characteristics between floating structures and internal solitary waves by using the CFD method.

At the present study we aim to determine the formation mechanism of various load components on the vertical cylinder due to internal solitary waves,as well as the influence mechanism of the vertical cylinder on the waveform and flow field characteristics.The paper is organized as follows:Chap.1 describes the numerical models to be used in this study on the base of considering the applicability conditions for internal solitary wave theories.Chap.2 contains the numerical results,including wave properties such as shape and amplitude,and internal solitary wave loads on the vertical cylinder,in addition,the comparisons between numerical results and experimental results are presented.Finally,some conclusions are given in Chap.3.

1 Numerical methods

The present numerical method adopts Navier-Stokes equations to simulate the strongly nonlinear interaction of internal solitary waves with the vertical cylinder,where the velocityinlet boundary uses the depth-averaged velocities of the upper-and lower-layer fluids induced by internal solitary waves.

1.1 Governing equations

For an incompressible fluid of density ρi,the velocity componentsu,v,（）w in Cartesian coordinates Oxyz and the pressure Pisatisfy the continuity equation and Navier-Stokes equations:

where g is gravitational acceleration and subscripts with respect to space and time represent partial differentiation.In the equations,stands for the upper(lower)layer fluid.

The boundary conditions at the interfaceare the continuity of normal velocity and pressure:

where ζ is the displacement of the interface.The top and bottom of calculation domain are required to satisfy the following boundary conditions:

The calculation domain is shown in Fig.1,which consists of two parts:the wave propagation and absorption zones.Internal solitary waves are aroused by using velocity-inlet method,the depth-averaged velocities induced by internal solitary waves on the inlet boundary is defined as

where c denotes wave phase velocity,is inlet velocity for the upper(lower)fluid at the inlet boundary.

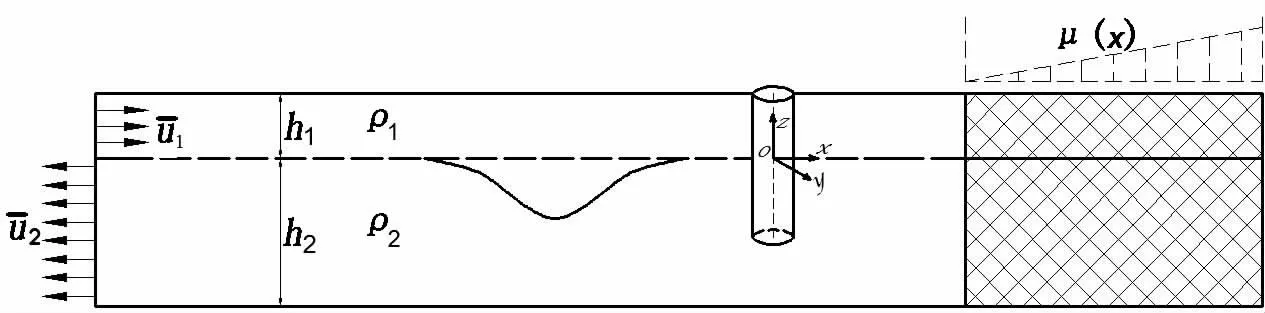
Fig.1 Sketch of numerical flume for the internal solitary waves

The VOF(volume of fluid)method is employed for tracking the two-layer fluid interface during the generating and propagating of internal solitary waves.Meanwhile,sponge layer technique is applied to dissipate internal solitary waves at the tail of numerical flume,which is realized by adding a source termto the momentum equation(2).The attenuation coefficient）is determined according to Ref.[12].

The horizontal forces Fxand vertical forceson the vertical cylinder consist of two parts,the pressure-difference force and the frictional force.

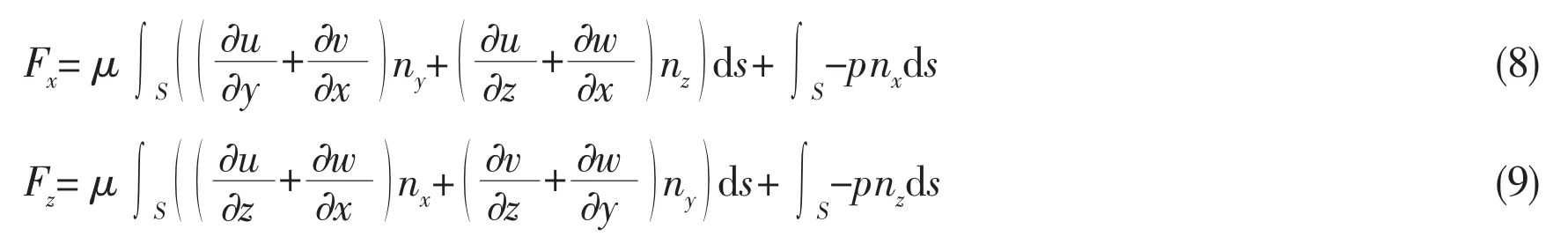
where S is the wetted surface area of the vertical cylinder,nx,ny,nzare the unit external normal vector of surface.In the formulas,the first term represents the frictional force and the second one represents the pressure-difference force.

The torque Myon the vertical cylinder is defined as follows:

According to the applicability conditions for three types of internal solitary wave theories including KdV,eKdV and MCC[7],the inlet velocity is determined as follows:

For a given internal solitary wave,the nonlinear parameter ε and dispersion parameter μ for the three types of internal solitary wave theories are calculated respectively.The KdV model is selected to calculated the velocity of inlet boundary for ε≤μ and μ＜ μ0,the eKdV model is selected foras well as the MCC model is selected forμ0(where μ0denotes the critical dispersion parameter summarized by laboratory experiments).

2 Numerical results and discussions

The paper carried out a series of experiments for the load characteristics of the vertical cylinder due to internal solitary waves in the large-scale density stratified tank.In order to compare with experimental results,the principal dimension of the numerical flume,upper(lower)layer fluid density,and the depth ratio are consistent with experimental conditions,namely,the length of the numerical flume is 30 m,the depth is 1 m,the diameter of the vertical cylinder D is 0.15 m,the draft of the vertical cylinder d is 0.535 m,the upper layer fluid density ρ1is 998 kg/m3,the lower layer fluid density ρ2is 1 025 kg/m3,and three kinds of depth ratio including h1:h2=1:9,2:8,3:7 are considered.

2.1 Numerical simulations for internal solitary waves

In order to analyze the influence of the viscosity on the generation and propagation for internal solitary waves,two different types of numerical models are simulated,including the N-S and Euler simulations.The waveform results for two different methods are shown in Fig.2 when h1:h2=3:7 and ad/h=0.101(Where addenotes the designed amplitude for internal solitary waves,and h=h1+h2).Results indicate that the waveforms generated by the two numerical methods remain stable and the decay of the amplitudes is weak during the propagation of the internal solitary wave,the relative error between the simulated and designed amplitudes is within 5%.Therefore,the two methods to numerically generate internal solitary waves are feasible.Hereinafter,all cases are simulated by N-S model unless special declare.

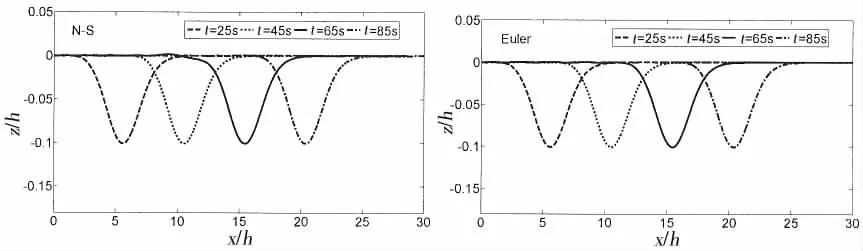
Fig.2 The numerical results for the internal solitary wave waveforms when h1:h2=3:7 and ad/h=0.101

Fig.3 shows the comparisons for internal solitary wave waveforms with theoretical and experimental results under three different cases.According to the applicability conditions for three types of internal solitary wave theories[7],Case A(h1:h2=3:7 and ad/h=0.101)appears weak nonlinear and weak dispersion,the eKdV theory is selected to calculate the velocity of inlet boundary,Case B(h1:h2=2:8 and ad/h=0.052)appears moderate nonlinear and weak dispersion,the KdV theory is selected to calculate the velocity of inlet boundary,Case C(h1:h2=1:9 and ad/h=0.086)appears strong nonlinear and weak dispersion,the MCC theory is selected to calculate the velocity of inlet boundary.Results show that the waveforms are in good agreement with the experimental and theoretical results,which means that the waveform is accurate and controllable for the present numerical method.

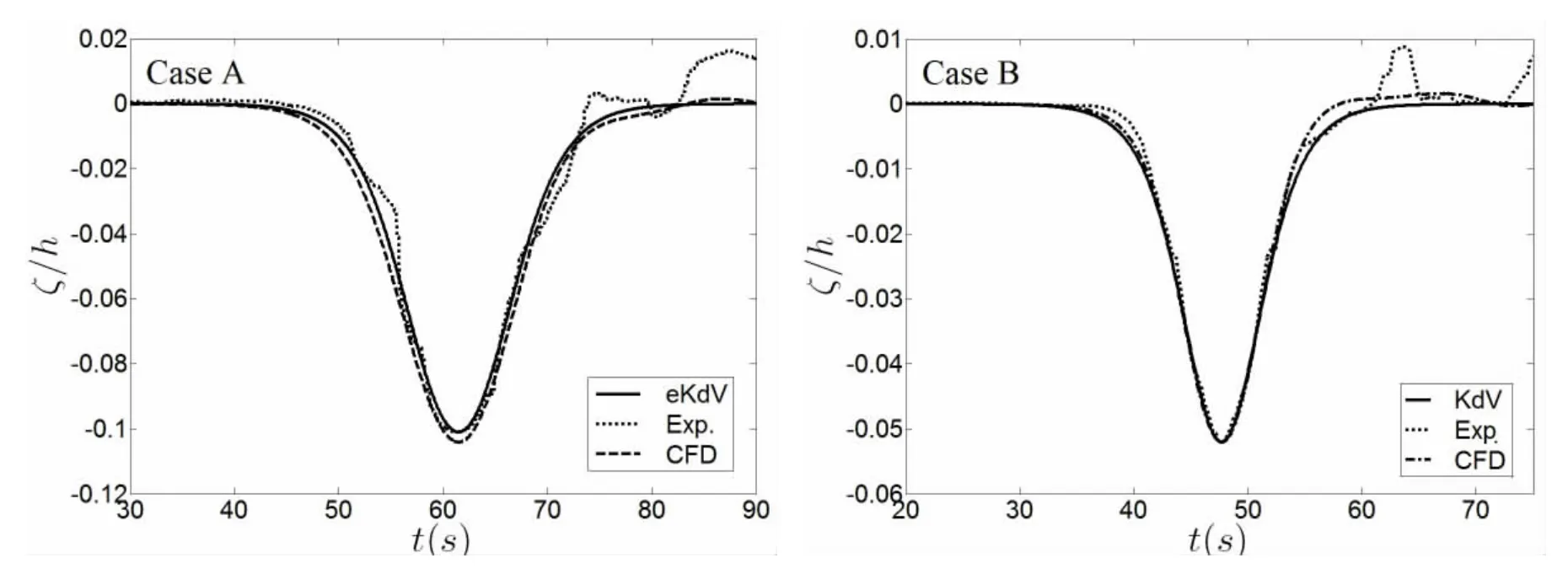
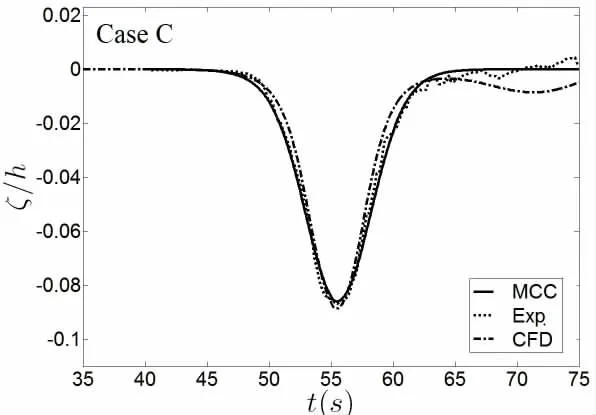
Fig.3 Comparisons for internal solitary wave waveforms with theoretical and experimental ones

The numerical results of wave amplitudes for the internal solitary waves are shown in Fig.4,where Symbol‘О’ represents the simulated amplitude,and the dotted line represents the designed amplitude.Results show the simulated amplitudes have good agreement with the designed amplitude,and the maximum error is within 5%.

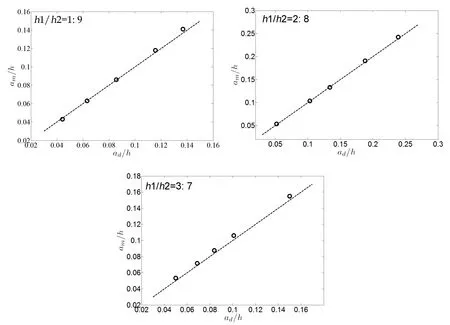
Fig.4 The numerical results of wave amplitudes for the internal solitary waves

2.2 Load characteristics on the vertical cylinder

In order to conveniently explain,the expressionare defined as the dimensionless horizontal and vertical forces,as well as torquesrespectively on the vertical cylinder due to internal solitary waves.Results of numerical and experimental amplitudes for dimensionless loads are shown in Fig.5.Results show that the numerical simulated amplitudes for the horizontal and vertical forces,as well as torques are in good agreement with experimental ones,and the maximum error is within 10%.

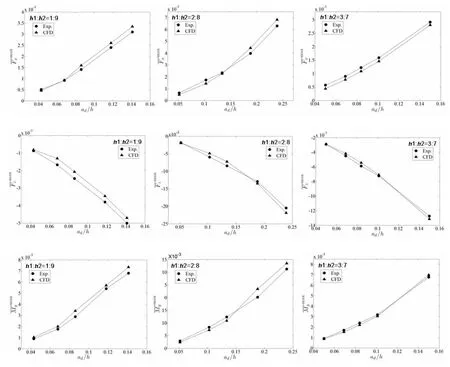
Fig.5 Results of numerical and experimental amplitudes for dimensionless loads

Fig.6 shows that the time variation characteristics for dimensionless loads for Case A.Results show that the simulated time-variation loads are in good agreement with experimentalresults,which means that it is reasonable and feasible to calculate the loads on the vertical cylinder based on the present numerical method.

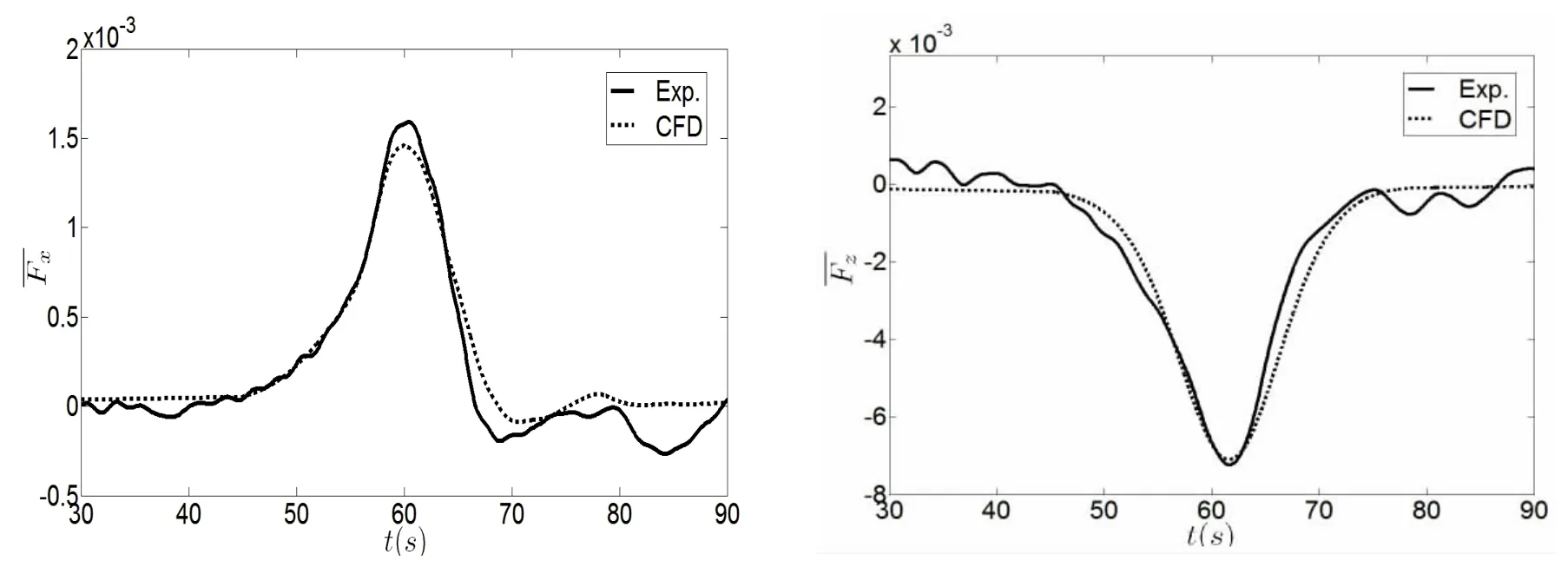
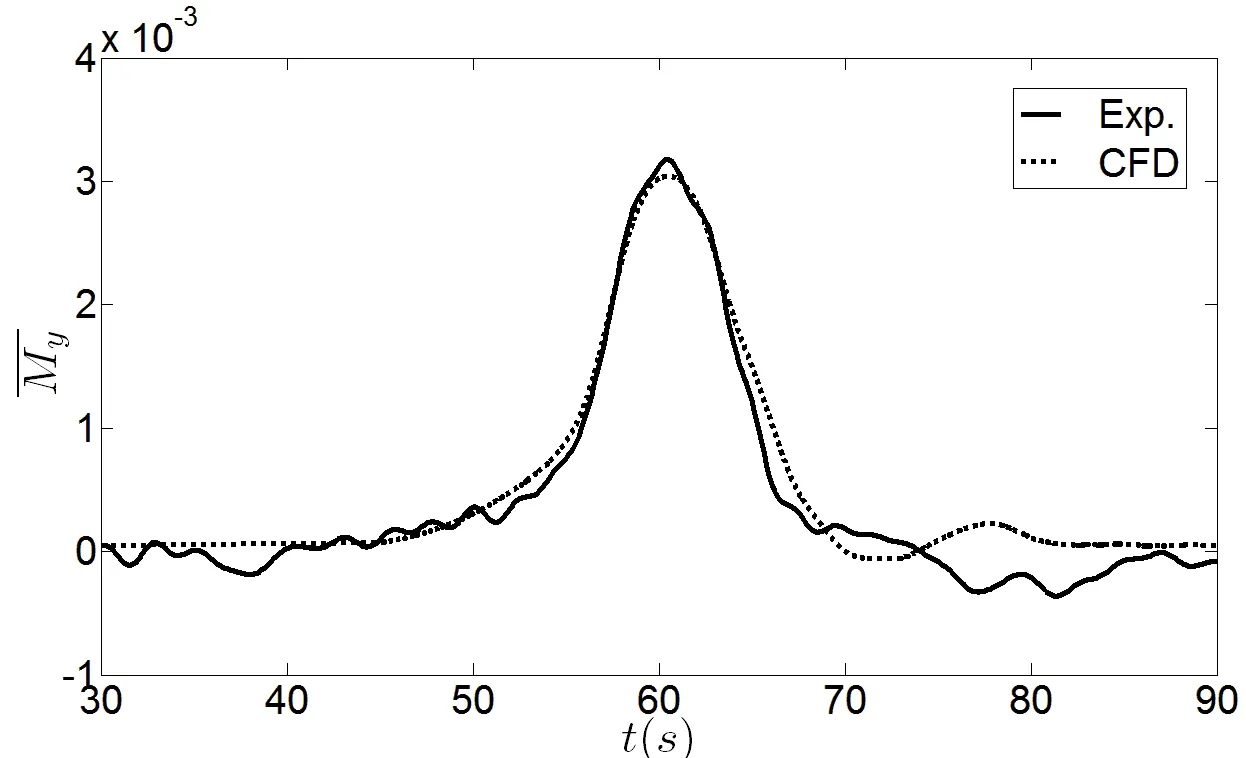
Fig.6 The time-variation characteristics for dimensionless loads for Case A

From the formulas(8)and(9),it can be seen that the pressure-difference and frictional forces are two components for horizontal and vertical forces due to internal solitary waves.The time-variation characteristics for wave pressure-difference and viscous pressure-difference forces for Case A are shown in Fig.7.The results indicate that frictional forceis not significant comparing with the pressure-difference forceand hence can be neglected,the main component of horizontal and vertical forces is pressure-difference force.

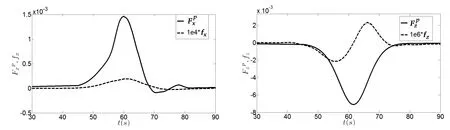
Fig.7 The time-variation characteristics for pressure-difference and frictional forces for Case A

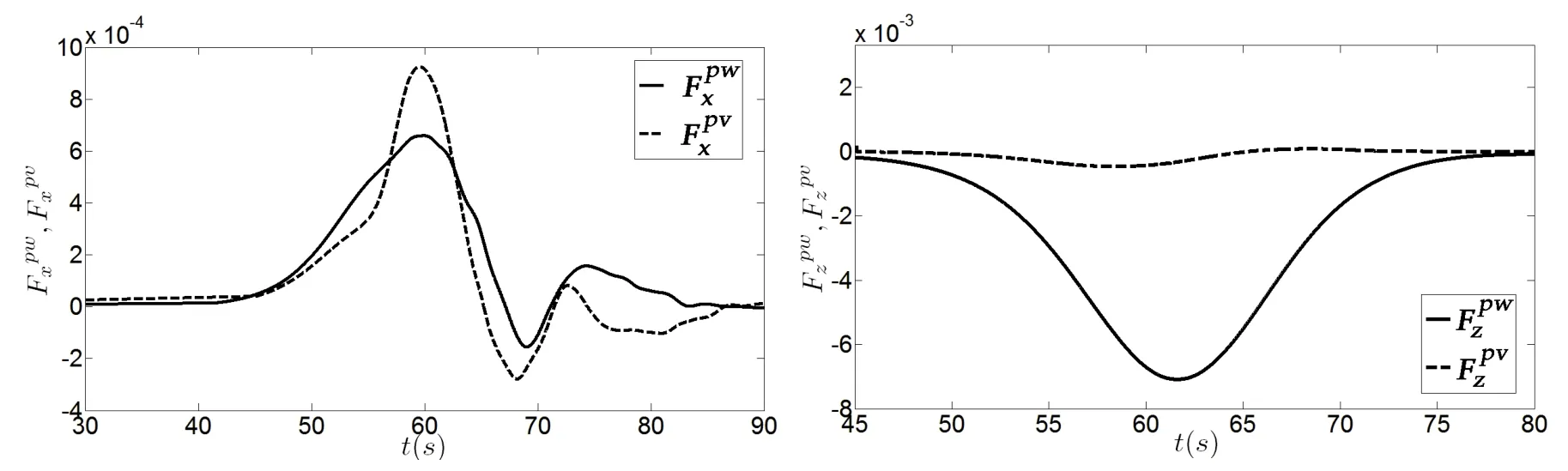
Fig.8 The time-variation characteristics for wave and viscous pressure-difference forces for Case A

Furthermore,the pressure-difference force can be divided into two components,including the wave pressure-difference forceand the viscous pressure-difference forceThe wave pressure-difference force is associated with the fluctuation of water parcel,which can be calculated by the Euler simulation,while the viscous pressure-difference force is associated with the viscosity effect of fluid,which can be calculated by the N-S simulation.The time-variation characteristics for wave and viscous pressure-difference forces due to internal solitary waves for Case A are shown in Fig.8.For the horizontal force,the orders of the magnitudes between the wave and viscous pressure-difference forces are the same,which means that the effect of the fluid viscosity is significant.For the vertical force,the component of the viscous pressure-difference force is not significant,which indicates that the effect of the fluid viscosity can be neglected.

2.3 Influence of the cylinder on internal solitary waves

The influence of the vertical cylinder on the internal solitary wave waveform for Case A is shown in Fig.9,where the axis of the vertical cylinder is in front of the wave trough when t=46 s and t=58 s,the axis is located near the wave trough when t=60 s,and the axis is behind the wave trough when t=62 s and t=74 s.Results show that some disturbances of the wave surface happen near the cylinder during the propagation of internal solitary waves,especially,the disturbances of the wave surface are most evident when the internal solitary wave passes right through the axis of the cylinder.Nevertheless,the disturbances are not significant comparing to the amplitude of the internal solitary wave,and hence can be neglected.

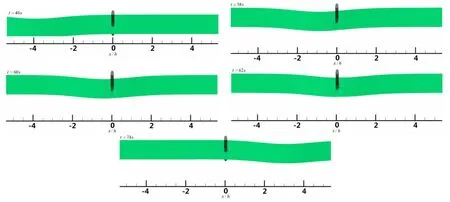
Fig.9 The effect of the cylinder on the internal solitary wave waveform for Case A

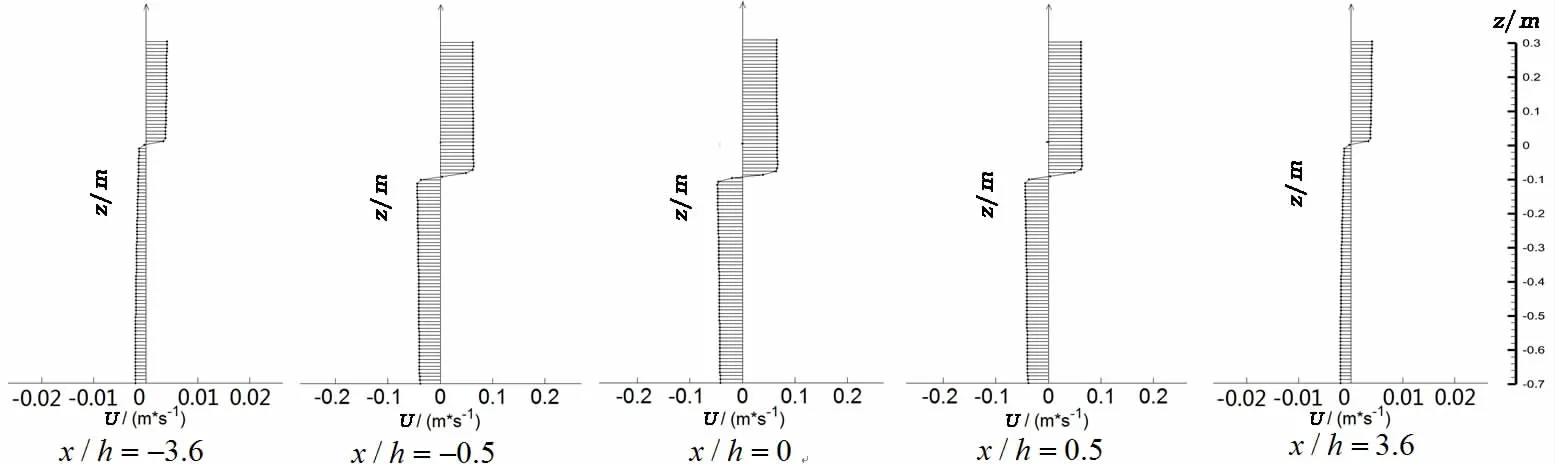
Fig.10 The flow field characteristics induced by the internal solitary wave when t=60 s for Case A

The flow field characteristics due to the internal solitary waves when t=60 s for Case A are shown in Fig.10.In the propagation process,the internal solitary wave is going in the same direction as the upper fluid,but contrary to the lower fluid.Hence,the shear flow is formed near the interface of the upper and lower fluid.The vertical flow induced by the internal solitary wave also exists,which descends and climbs at the front and rear of the wave trough respectively.In addition,it can be seen from the Fig.10 that the decay rate of the vertical distribution of the horizontal velocity induced by the internal solitary wave is small in different positions.

Fig.11 The effects of the vertical cylinder on flow field due to the internal solitary waves for Case A

The effect of the cylinder on the flow field due to the internal solitary wave for Case A is shown in Fig.11.During wave propagation,a pair of opposite trailing vortex forms at the tail of the cylinder due to the detour flow of the vertical cylinder on the induced flow field.The induced horizontal velocity move from left to right when z/h=0.1 and z/h=-0.05,so the trailing vortex is on the right side of the vertical cylinder.Instead,the induced horizontal velocity move from right to left when z/h=-0.12,thus the trailing vortex is on the left side of the vertical cylinder.

The vortex-induced vibration is a common physical phenomenon in ocean engineering,which is caused by periodic trailing vortex behind the vertical cylinder.Due to the existence of the trailing vortex at the rear of the vertical cylinder,it is necessary to study the effect of trailing vortex on the vertical cylinder.The Fig.12 shows that the dimensionless lifton the vertical cylinder due to the trailing vortex is not significant and can be neglected.

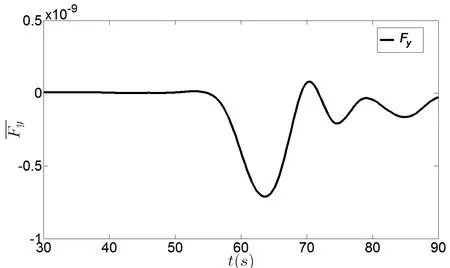
Fig.12 The time-variation characteristics of the dimensionless lift force for Case A

For the interaction between the vertical cylinder and surface gravity waves,the character number β=D/λ is usually defined to describe the relative size of the wavelength and the vertical cylinder’s diameter.The diffraction effect of the surface wave can be neglected when β＜0.15,therefore,it is feasible that the horizontal and vertical forces on the vertical cylinder due to surface gravity waves can be calculated by the Morison and Froude-Krylov formulas respectively.At the real ocean circumstance,the characteristic wavelength of internal solitary waves can reach several hundreds meters,even thousands of meters,while the diameter of the vertical cylinder is within 40 m in general,hence,the characteristic number β is far lower than 0.15.According to the pervious discussion,the influence of the vertical cylinder on the waveform and the flow field induce by the internal solitary wave can be neglected.Hence,a simplified method for calculating the loads on the vertical cylinder due to internal solitary waves can be presented as follows:the horizontal force is calculated by the Morison formulas and the vertical force is calculated by the Froude-Krylov formulas respectively.Then we will verify the rationality of this simplified method using the numerical method combined with experimental results.

We denote U1and W1as horizontal and vertical instantaneous velocities of water particles induced by internal solitary waves when ζ＜ z＜h1,U2and W2as horizontal and vertical instantaneous velocities of water particles induced by internal solitary waves when-h2＜ z＜ ζ,where Uiand Wiare defined as follows[13]:

Combined with the formulas(11)and(12),the Morison formulas for calculating the horizontal force on vertical cylinder due to internal solitary waves can be written as follows:

where Cmis the coefficient of the inertia force,Cdis the coefficient of the drag force,Vnis the normal velocity vector of water parcels,andis the normal acceleration vector of water parcels.

Based on a series of experiments,Huang[7]summarized a solution for two coefficients in the Morison formula:

where Re=UmaxD/ν is the Reynolds number,Umaxis maximum velocity of water parcel due to internal solitary waves,ν is the coefficient of the kinematical viscosity.

The Froude-Krylov formulas for calculating the vertical forces on vertical cylinder due to internal solitary waves can be described as follows:

According the Bernoulli equation,the dynamic pressure P induced by internal solitary waves can be calculated as

Results based on the simplified method for amplitudes for dimensionless loads are shown in Fig.13.It can be seen that the load amplitudes based on the simplified method are in good agreement with the numerical results,and the maximum error is within 8%.Hence,it is feasible to calculate the loads on vertical cylinder due to internal solitary waves by using the simplified method.

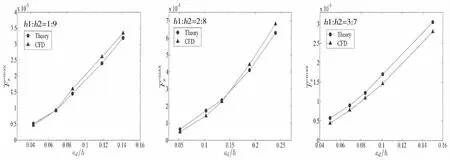
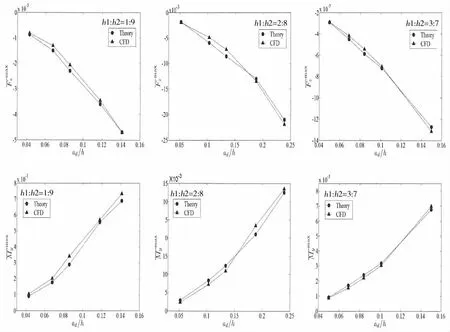
Fig.13 Results based on the simplified method for amplitudes for dimensionless loads due to internal solitary waves

3 Conclusions

According to the applicability conditions for three types of internal solitary wave theories,including KdV,eKdV and MCC,a numerical method based on the Navier-Stokes equation in a two-layer fluid is presented to simulate the strongly nonlinear interaction of internal solitary waves with a vertical cylinder,where the velocity-inlet boundary is applied by using of the depth-averaged velocities in the upper-and lower-layer fluids induced by the internal solitary wave.The conclusions can be summarized as follows:

(1)The waveform and amplitude of the internal solitary wave based on the present numerical method are in good agreement with the experimental and theoretical results.Also,numerical results for the horizontal and vertical forces,as well as torques on the vertical cylinder due to the internal solitary wave have a good agreement with experimental results.Hence,it is feasible to simulate the strongly nonlinear interaction of internal solitary waves with a vertical cylinder by using the present numerical method.

(2)The horizontal and vertical forces on the vertical cylinder due to internal solitary wavescan be divided into three components,including the wave and viscous pressure-difference forces,as well as the frictional force,where the frictional force is not significant and can be negligible;for the horizontal force,the orders of the magnitudes between the wave and viscous pressure-difference forces are the same,which means that the effect of the fluid viscosity is significant;for the vertical force,the component of the viscous pressure-difference force is not significant,which means that the effect of the fluid viscosity can be neglected.

(3)The effects of the vertical cylinder on the waveform and flow field induced by the internal solitary wave are small.Therefore,it is feasible to calculate the horizontal and vertical forces on the vertical cylinder due to internal solitary waves by the Morison and Froude-Krylov formulas respectively.

[1]Jameel M,Ahmad S,Islam M K A B M S.Fully coupled nonlinear dynamic response of spar platform under random loads[C]//The Twenty-second International Offshore and Polar Engineering Conference.International Society of Offshore and Polar Engineers,2012:1004-1011.

[2]Cai S,Xie J,He J.An overview of internal solitary waves in the South China Sea[J].Surveys in Geophysics,2012,33(5):927-943.

[3]Bole J B,Ebbesmeyer C C,Romea R D.Soliton currents in the South China Sea:Measurements and theoretical modeling[C]//The 16th Offshore Technology Conference.Houston,1994:367-376.

[4]Choi W,Camassa R.Fully nonlinear internal waves in a two-fluid system[J].J Fluid Mech.,1999,396:1-36.

[5]Helfrich K R,Melville W K.Long nonlinear internal waves[J].Ann.Rev.Fluid Mech.,2006,38:395-425.

[6]Choi W,Camassa R.Weakly nonlinear internal waves in a two-fluid system[J].J Fluid Mech.,1996,313:83-103.

[7]Huang Wenhao,You Yunxiang,Wang Xu,et al.Wave-making experiments and theoretical models for internal solitary waves in a two-layer fluid of finite depth[J].Acta Phys.Sin.,2013,62(8),084705:1-14.(in Chinese)

[8]Cai Shuqun,Xu Jiexin,Chen Zhiwu,et al.The effect of a seasonal stratification variation on the load exerted by internal solitary waves on a cylindrical pile[J].Acta Oceanologica Sinica,2014,33(7):21-26.

[9]Xie J S,Jiang Y J,et al.Strongly nonlinear internal solution load on a small vertical cylinder in two-layer fluids[J].Applied Mathematical Modelling,2010,34(8):2089-2101.

[10]Li Xiaomin,Zhang Lin,Guo Haiyan,et al.Comparison of numerical wave-generating methods for internal solitary waves with theoretical and experimental results[J].Oceanologia Et Limnologia Sinica,2016,47(5):898-905.(in Chinese)

[11]Miao Desheng,Guo Haiyan,Zhao Jing,et al.Study of numerical simulation method of internal solitary waves[J].Journal of Ocean University of China,2016,46(10):123-128.(in Chinese)

[12]Han Peng.The study of damping absorber for irregular waves based on VOF method[D].Dalian:Dalian University of Technology,2008:38-47.(in Chinese)

[13]Camassa R,Choi W,Michallet H,et al.On the realm of validity of strongly nonlinear asymptotic approximations for internal waves[J].J Fluid Mech.,2006,549:1-23.

直立圆柱体内孤立波载荷特性数值模拟

王 旭1，2， 林忠义3， 尤云祥1， 於 锐4
（1.上海交通大学 海洋工程国家重点实验室，上海200240；2.中国科学院 力学研究所 流固耦合系统力学重点实验室，北京100190；3.嘉兴南洋职业技术学院，浙江 嘉兴314003；4.江苏省地方海事局，南京 210004）

以三类内孤立波理论（KdV、eKdV和MCC）的适用性条件为依据，将内孤立波诱导上下层深度平均水平速度作为入口条件，采用Navier-Stokes方程为流场控制方程，建立了两层流体中内孤立波对直立圆柱体强非线性作用的数值模拟方法。结果表明，数值模拟所得内孤立波波形及其振幅与相应理论和实验结果一致，并且直立圆柱体内孤立波水平力、垂向力及其力矩数值模拟结果与实验结果吻合。直立圆柱体内孤立波载荷由波浪压差力、粘性压差力和摩擦力构成，其中摩擦力很小，可以忽略；对于水平力，其波浪压差力与粘性压差力量级相当，流体粘性的影响显著；对于垂向力，粘性压差力很小，流体粘性影响可以忽略。此外，直立圆柱体对内孤立波的波形及其诱导流场的影响很小，因此采用Morison公式和傅汝德—克雷洛夫力分别计算其内孤立波水平力和垂向力是可行的。

两层流体；内孤立波；数值模拟；载荷特性

P751

A

国家自然科学基金资助项目（11372184，11602274，11232012，11572332）；高等学校博士点基金资助项目（20110073130003）

王 旭（1985-），男，上海交通大学博士研究生；林忠义（1959-），男，嘉兴南洋职业技术学院副教授；尤云祥（1963-），男，上海交通大学教授，博士生导师；於 锐（1984-），男，江苏省地方海事局工程师。

10.3969/j.issn.1007-7294.2017.09.003

Article ID： 1007-7294（2017）09-1071-15

Received date：2017-06-10

Foundation item:Supported by the National Natural Science Foundation of China(11372184,11602274,11232012,11572332);The Specialized Research Foundation for the Doctoral Program of Higher Education of China(20110073130003)

Biography：WANG Xu(1985-),male,Ph.D.student of Shanghai Jiao Tong University;LIN Zhong-yi(1959-),male,professor,School of Jiaxing Nanyang Profession and Technology;YOU Yun-xiang(1963-),male,professor/tutor,corresponding author,E-mail:youyx@sjtu.edu.cn.