Numerical Simulation of Fully Nonlinear NWT by DBIEM Method with MTF for the Downstream Boundary

XU Gang,BAI Xu,MA Xiao-jian,ZHU Ren-qing

(School of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China)

Numerical Simulation of Fully Nonlinear NWT by DBIEM Method with MTF for the Downstream Boundary

XU Gang,BAI Xu,MA Xiao-jian,ZHU Ren-qing

(School of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China)

Abstract:Wave propagation in a three-dimensional nonlinear numerical wave tank(NWT)is studied based on the fully nonlinear velocity potential theory.The governing Laplace equation with fully nonlinear boundary conditions on the moving free surface is solved by using the indirect desingularized boundary integral equation method(DBIEM).The fourth-order predictor-corrector Adams-Bashforth-Moulton scheme(ABM4)and mixed Eulerian-Lagrangian(MEL)method are used for the timestepping integration of the free surface boundary conditions.A smoothing algorithm,B-spline,is applied to eliminate the possible saw-tooth instabilities.An effective Multi-transmitting Formula method for radiation condition is employed to transmit wave out of computational region.The numerical results are compared with analytical solutions.The results show that MTF method can be used for simulating fully nonlinear wave propagation.

Key words:NWT;DBIEM;Multi-transmitting formula

0 Introduction

When simulating the nonlinear wave propagation through an unbounded domain in the time domain,it is necessary to truncate the computational domain into a finite domain in order to reduce computational costs.Thus,non-reflecting radiation condition is required for the truncated surface,however,there is no exact non-reflecting condition in existence.The Sommerfeld-Orlanski’s condition has been widely used for linear simulation,this condition is local in both time and space and dependent on the phase velocity of out-going wave but cannot ensure good results for irregular wave problem.The global matching or shell function method is very accurate for linear irregular wave radiation but with relatively large computational effort on comparing with the local method and can not satisfy the nonlinear condition.Another common used method is Damping Zone(DZ),which can absorb high frequency waves efficiently.It is limited by the length of DZ and therefore not very efficient for low frequency waves.Clément[1]proposed a coupled method(piston-beach hybrid absorber)to absorb outgoing wave.Boo[2]proposed a numerical scheme,which combines an absorbing beach and the stretching technique,to simulate the open boundary.Wang and Wu[3]imposed a radiation condition via a combination of Damping Zone(DZ)and Sommerfeld-Orlanski equation.However,the efficiency of DZ method strongly depends on the ratio of the length of damping zone and wave length.The longer wave length requires a wider beach.It will result in much more meshes on the free surface,especially when dealing with irregular wave problem.

In this work,the indirect desingularized boundary integral equation method(DBIEM),which has been successfully used previously in solving nonlinear water wave problems such as in the work by Zhang et al[4-5],is employed to solve the boundary value problem at each time step.Compared with the conventional BEM,the integral kernels of the DBIEM are no longer singular as the singularities are placed slightly outside the fluid domain.This is particularly advantageous when the direct differentiation is applied to the integral equation to obtain the velocity.The fourth-order predictor-corrector Adams-Bashforth-Moulton(ABM4)scheme and mixed Eulerian-Lagrangian(MEL)method are used for the time-stepping integration of the free surface boundary conditions.Since wave breaking is not considered in this work,the position of the nodes on free surface is tracked by applying semi-Lagrangian approach[6],in which the nodes on free surface are allowed to move only in vertical direction,with the horizontal motion of the nodes on the free surface held fixed.This approach has the advantage of avoiding the task of re-gridding the free surface at each time step.For stable time-step simulation,a B-spline smoothing scheme is applied in both longitudinal and transverse directions of the tank to prevent saw-tooth instability.During the simulation,Multi-transmitting Formula method[7-10]is employed as radiation condition to minimize wave reflection on the truncated surface.Numerical results obtained by the present method agree fairly with analytical solution and show that the present model is effective in the simulation for 3D fully nonlinear wave propagation.

1 Mathematical model

Fig.1 Sketch of a 3D numerical wave tank(left)and radiation condition(right)

A Cartesian coordinate system oxyz is defined for 3D wave propagation problem,as shown in Fig.1.The origin of oxyz is placed on the plane of the undisturbed free surface with the x-axis positive in the propagation direction of incident waves prescribed at the vertical upstream boundary,and the z-axis positive in the opposite direction of gravity.In Fig.1,D denotes the fluid domain whiledenote the boundaries of instantaneous free surface,side wall,bottom,upstream and downstream,respectively.

We assume the fluid is incompressible and inviscid,and the flow irrotational,the fluid motion can be described by a velocity potential φ,which satisfies the Laplace equation within the fluid domain D,

All the boundary conditions can be desribed as follows:

(1)On the instantaneous free surface ΓF,the dynamic and kinematic conditions can be written as:

where g is the gravitational acceleration and η is the wave elevation.

(2)On side wall ΓWand bottom ΓB,the zero-normal flux condition can be expressed as:

(3)On upstream boundary ΓU,the fluid motion is prescribed by giving the properties(surface elevation and normal velocity)of known incident wave forms.

(4)For downstream boundary condition,the fluid domain has to be truncated at a finite downstream boundary of ΓDin the NWT.An appropriate radiation condition should be imposed on the ΓDto minimize the wave reflection during the simulation in time domain.In this work,an effective Multi-transmitting formular method(MTF)is employed to simulate downstream boundary condition.

The above boundary value problem will be solved by the indirect desingularized boundary integral equation method(DBIEM),the details of this method can be found in Ref.[4].In order to obtain the velocity potential and free surface elevation at each time step,the fourthorder predictor-corrector Adams-Bashforth-Moulton scheme(ABM4)and mixed Eulerian-Lagrangian(MEL)method are used.Using the total derivativethe fully nonlinear free surface conditions can be modified as follows in Lagrangian frame,

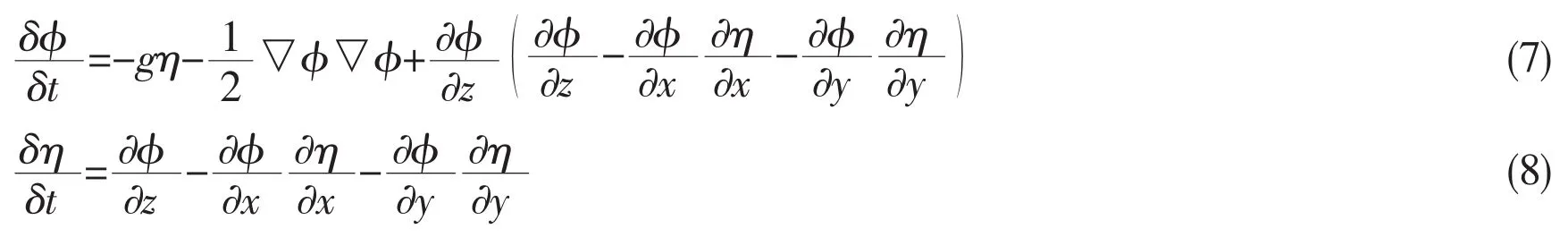
ABM4 scheme[4]is selected for integrating Eq.(7)and Eq.(8)over time.

2 Desingularized boundary integral equation method

In this study,the indirect DBIEM is employed to solve the boundary value problem for the unknown velocity potentialat each time step.This method obtains the solution by distributing Rankine sources over a surface S outside the fluid domain D.This surface is at a small distance away from the corresponding real boundary of the fluid.The velocity potential in the fluid domain D can be written as follows:

For the problem considered in this work,we construct the solution using a constantstrength source point within each element over the integration boundary SFand a constantstrength source point over the integration surface SW,where SFis the integration surface above the free surface ΓF,and SWis the integration surface outside the real boundary of the tank.That is

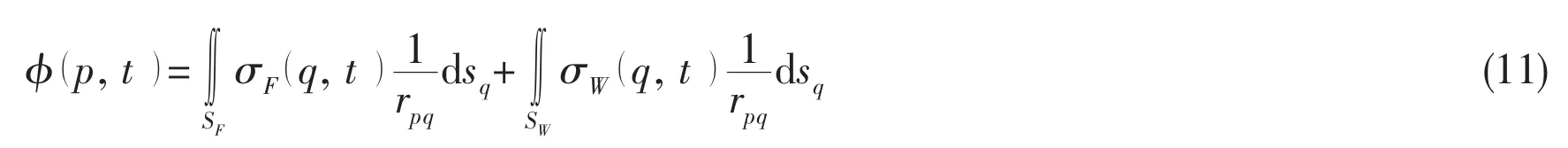
By applying the boundary conditions,we obtain boundary integral equations for the unknown strength of the singularities,respectively:

In the desingularized method,the source distribution is outside the fluid domain so that the source points never coincide with the field points and therefore the integrals are non-singular.In addition,because of the desingularization,we can use simple isolated Rankine sources andobtain the equivalent accuracy.This greatly reduces the complexity of the form of the influence coefficients that make up the elements of the kernel matrix[4].Then the integral equations in Eq.(12)and Eq.(13)can be replaced by a discrete summation of N-isolated singularities located at a small distance away from the corresponding control point on the boundaries,

The desingularized distance between isolated source point and corresponding control point is given by

where ldand β are constants and Dmis a measure of the local mesh size(typically the square root of the local mesh area).The accuracy and convergence of the solutions are sensitive to the choices of ldand β.Therefore,appropriate ldand β values need to be determined after numerical test.The recommended values are ld=0.5-1.0 and β=0.5.A detailed study with regard to the performance of DBIEM with the desingularization parameters was reported in Ref.[11].ldis fixed at 0.85 in our work.

Once the above integral equations using isolated Rankine source are solved at each time step,the fluid velocity in Eq.(2)and Eq.(3)can be calculated from direct derivatives,

3 Multi-transmitting Formula for radiation condition

Liao[7]described a general expression of one-way wave propagation and developed a system of local non-reflecting boundary conditions using space-time extrapolation.Its initial aim is to deal with the propagation of earthquake wave out of truncated boundary.

In this section,the MTF method for treating the velocity potential φ in water wave field will be introduced,as shown in Fig.1.Suppose that point O0is on the truncated surface ΓDand j is the point which is away from point O0along its normal vector to the fluid domain.The distance between point j and point O0is jCaΔt along the normal vector of point O0,where Ca,related to physical wave speed Cx,is the artificial wave speed and Δt is the time interval.Usually,we do not need set Caequal to Cx.

According to the theory of MTF,the velocity potential on ΓDmay be written as

where integer p represents the time level,N is the order of the MTF method and C is thebinomial coefficient.

In order to eliminate the effect of the frequencies,which are near to zero including zero,a constant value γ2is used.Thus,the second order MTF can be written as Eq.(18),where γ2is additional factor and set to 0.025;

4 Numerical results and discussions

The present model is applied to simulate the wave propagation for linear incident wave and second-order Stokes wave in a fully nonlinear NWT.In our simulation,the length of NWT(L)is 2 m,depth-length ratio h/L=0.5,and breadth-length ratio B/L=0.25.The NWT is divided in x-direction by Nx=40 intervals,in y-direction by Ny=11 intervals and in z-direction by Nz=10 intervals.

In the MTF method,we need to use an artificial wave speed Cato find the exact position of the inner points corresponding to the control point on the truncated surface,as shown in Fig.1.Normally,we do not need to set Caequal to the physical wave speed Cxand yet we can still get reasonable results when Cais in the certain range of Cx(Ca∈0.8 Cx～1.2Cx).The numerical results for different Caare presented in Fig.2 and Fig.3.We can find that the MTF method is effective to transmit waves out of truncated surface when Cais in the prescribed range.Thus,the MTF method is proposed as radiation condition to also accord greater flexibility for the simulation of fully nonlinear NWT.

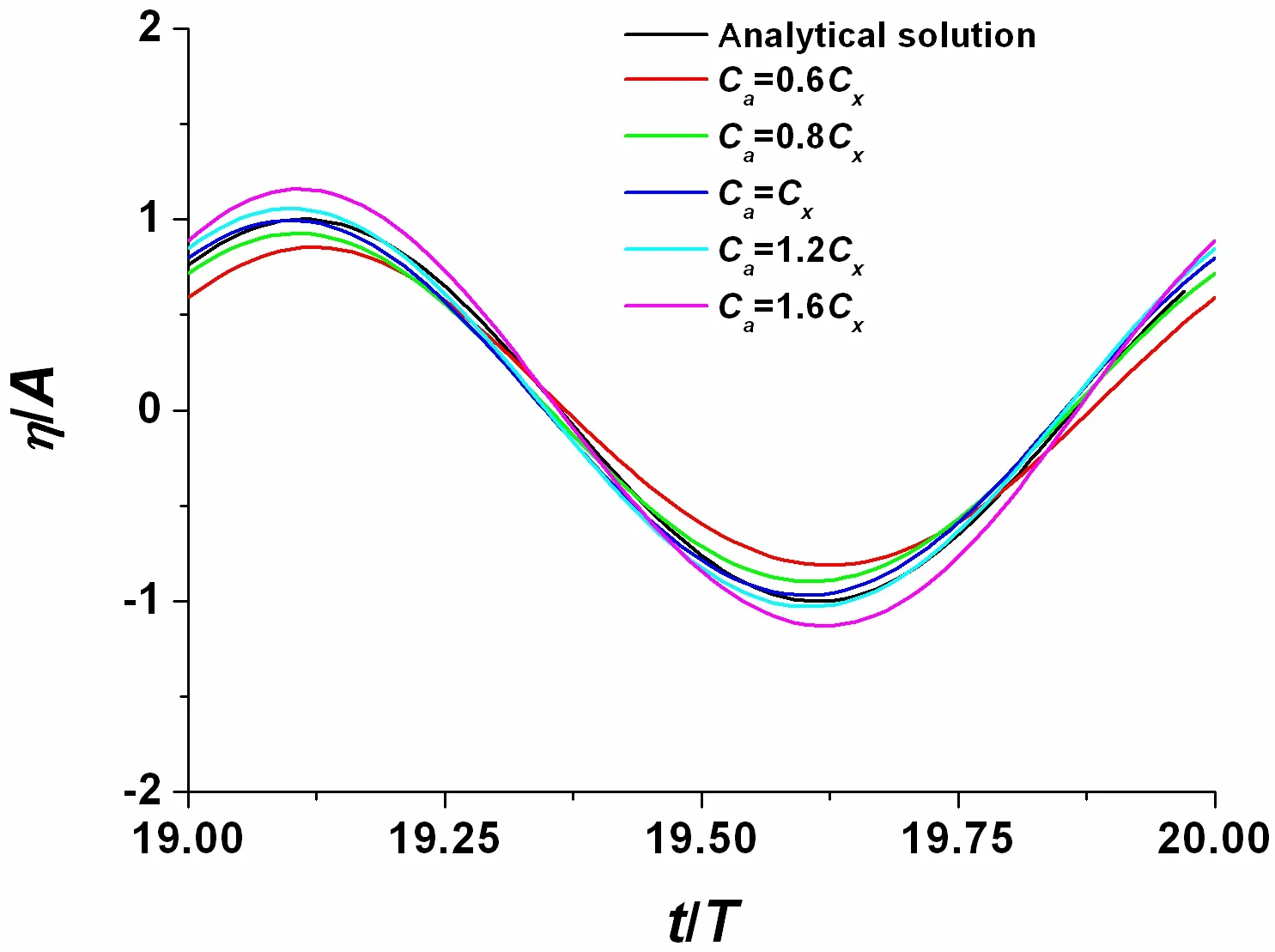
Fig.2 Comparison of wave elevation between linear analytical solution and numerical results with different artificial wave speed(λ=4.0 m)

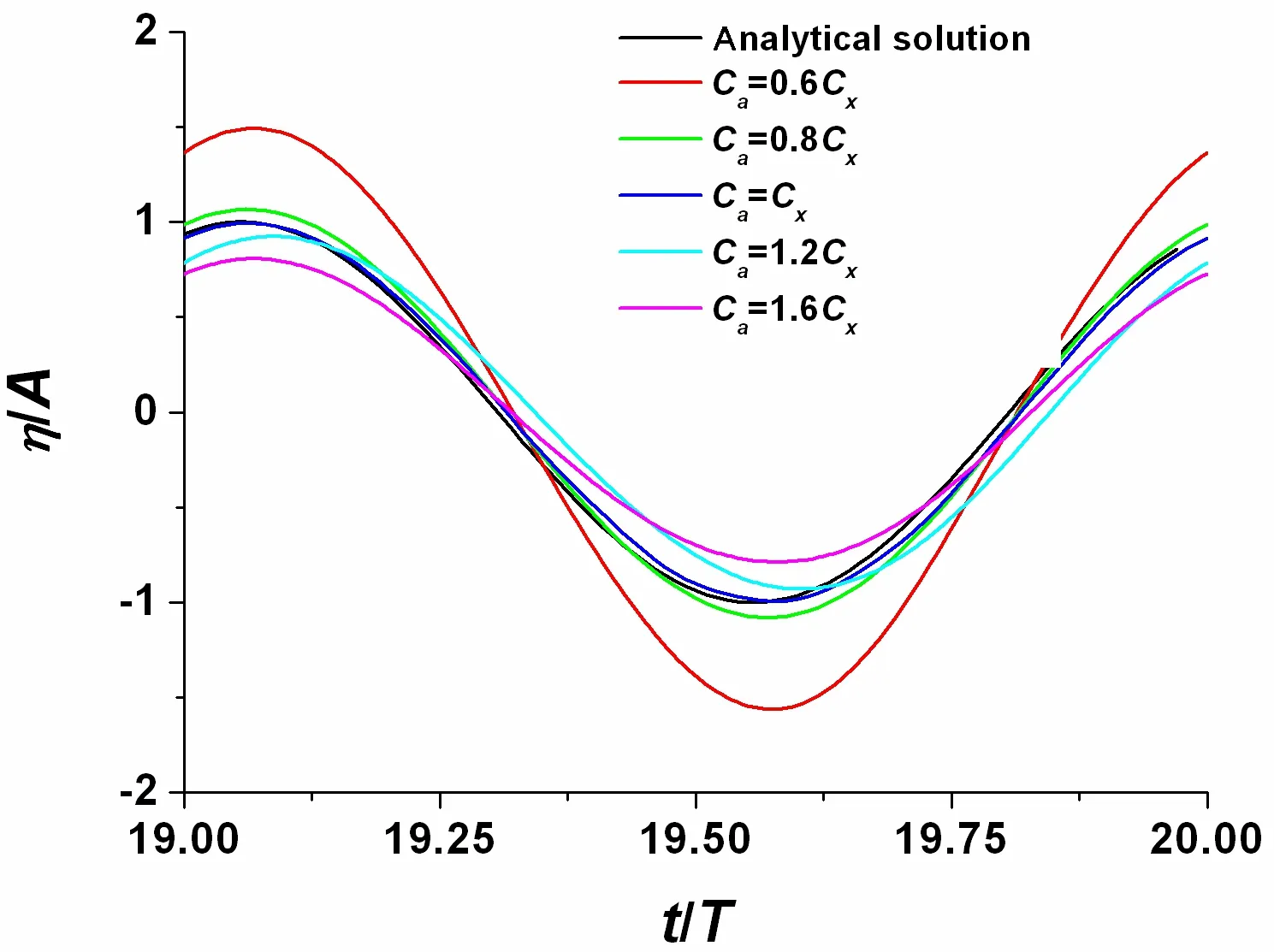
Fig.3 Comparison of wave elevation between linear analytical solution and numerical results with different artificial wave speed(λ=8.0 m)

4.1 Simulation of linear regular incident wave

The model is next applied to simulate the linear regular incident wave.We consider three cases:wave length λ=1 m,4 m and 8 m.For these simulations,the wave amplitude A is set to 0.02 m,time step Δt is taken as T/100 and Cais equal to Cx[9],where T is wave period.The numerical results are compared with corresponding linearized analytical solution,as shown in Figs.4-6.We can see that the numerical result obtained by present method agrees fairly with the theory after the initial transient effect.This indicates that the method works well with the given problem.It needs to be mentioned that a modulation function is used in the numerical simulation[12].

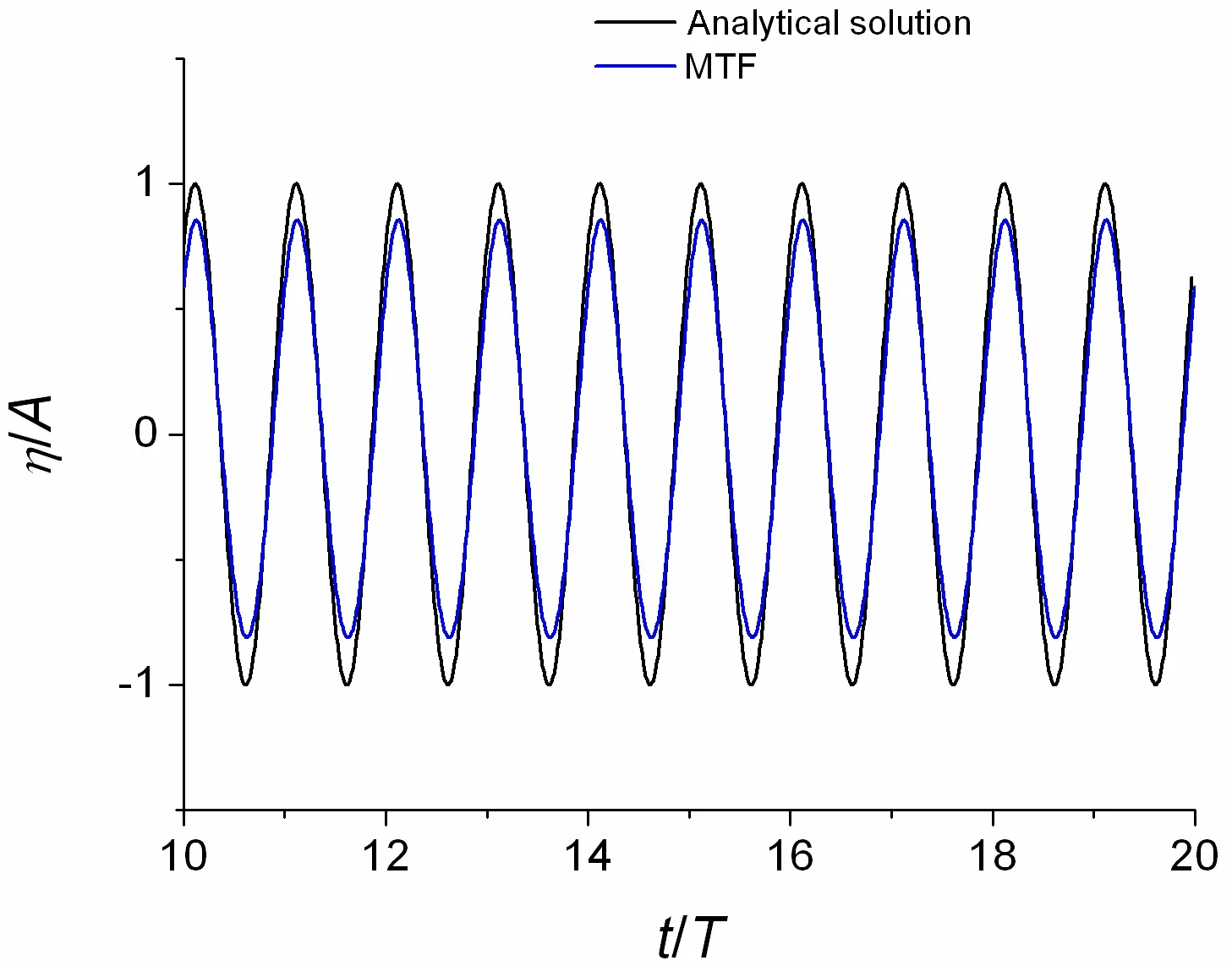
Fig.4 Wave elevation for the case of wave length λ=4 m(black solid line:analytical solution;blue solid line:MTF as radiation condition)

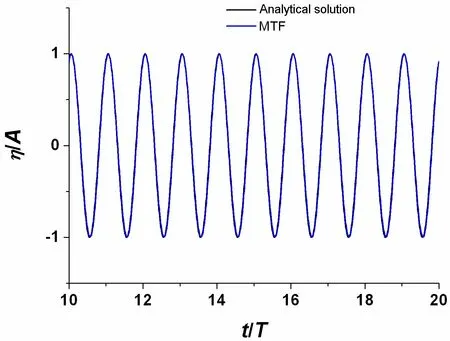
Fig.5 Wave elevation histories for the case of wave length λ=8 m(black solid line:analytical solution;blue solid line:MTF as radiation condition)

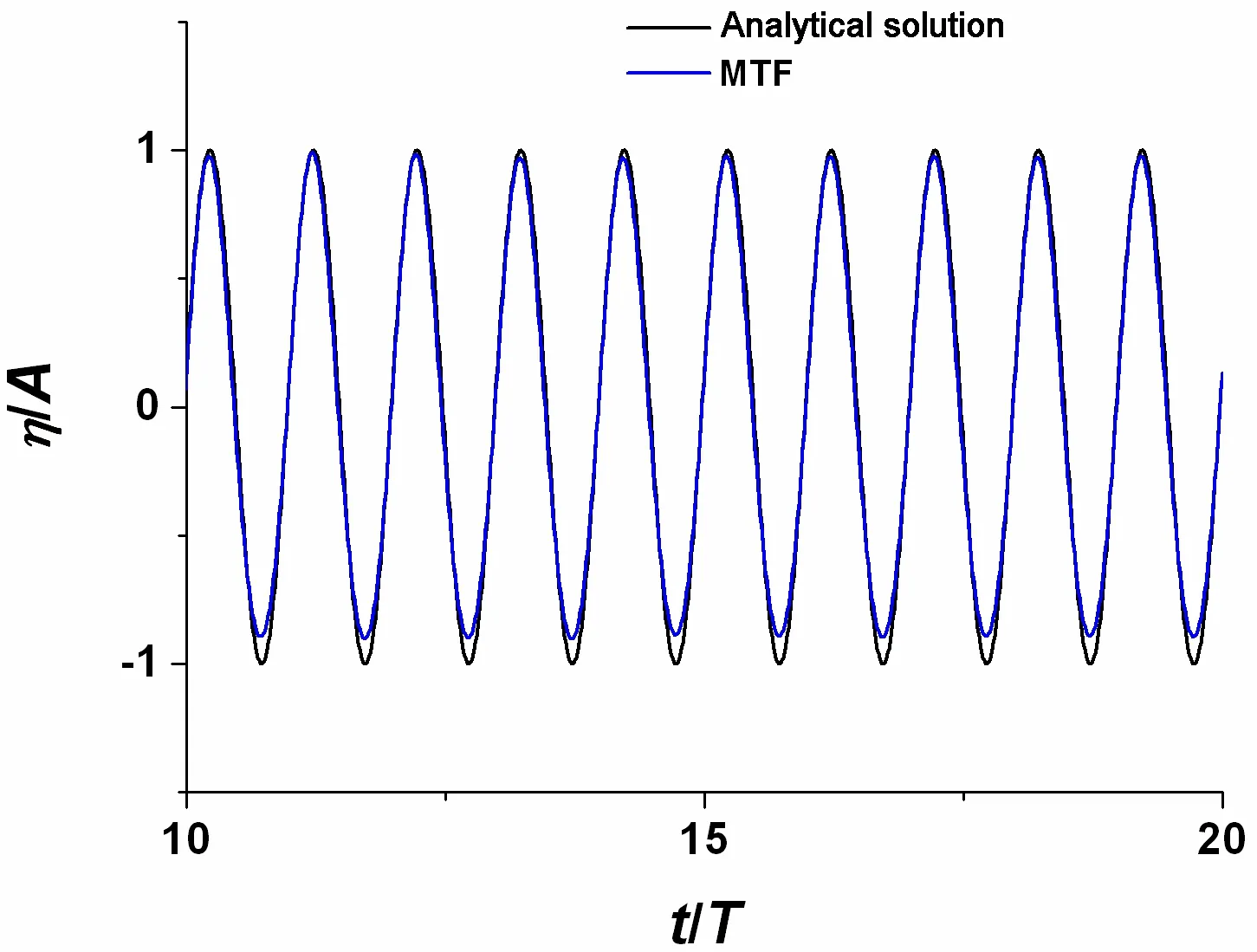
Fig.6 Wave elevation histories for the case of wave length λ=1 m(black solid line:analytical solution;blue solid line:MTF as radiation condition)

Fig.7 Wave elevation histories at(x=0.475 m,y=0)for λ=1 m and A=0.02 m(black solid line:analytical solution;blue solid line:MTF as radiation condition)

4.2 Simulation of second-order stokes incident wave

The model is finally applied to simulate the wave propogation ofsecond-order Stokes waves,which have the basic characteristic of nonlinear waves of higher and sharper crest,lower and flatter trough.The parameters for simulating second-order Stokes waves propagation are taken as λ=1 m,A=0.02 m and Δt=T/100.Fig.7 shows the wave elevation histories at(x=0.475 m,y=0)and the numerical results are compared with second-order analytical solution.We can find that the results agree with the analytical solution and have strong stability.In order to illustrate the wave propagation,snapshots of free surface are shown in Fig.8 at four different times(t=4T,6T,8T and 10T).

Fig.8 Free surface profiles(a)t=4T;(b)t=6T;(c)t=8T;(d)t=10T

5 Conclusions

In this paper,3D fully nonlinear NWT are solved by using a DBIEM coupled with MEL time marching scheme.The position of instantaneous free surface is tracked by applying semi-Lagrangian approach.An effective MTF method is employed as radiation condition to transmit wave out of truncated surface.It is found that the present model is accurate,numerically stable and can be used for the simulation of 3D fully nonlinear wave propagation due to linear incident wave and second-order incident wave.

[1]Clément A.Coupling of two absorbing boundary conditions for 2D time-domain simulations of free surface gravity waves[J].Journal of Computational Physics,1996,126:139-151.

[2]Boo S Y.Linear and nonlinear irregular waves and forces in a numerical wave tank[J].Ocean Engineering,2002,29:475-493.

[3]Wang C Z,Wu G X.Time domain analysis of second-order wave diffraction by an array of vertical cylinders[J].Journal of Fluids and Structures,2007,23(4):605-631.

[4]Zhang X T,Khoo B C,Lou J.Wave propagation in a fully nonlinear numerical wave tank:a desingularized method[J].O-cean Engineering,2006,33:2310-2331.

[5]Zhang X T,Khoo B C,Lou J.Application of desingularized approach to water wave propagation over three-dimensional topography[J].Ocean Engineering,2007,34:1449-1458.

[6]Koo W C,Kim M H.Fully nonlinear wave-body interactions with surface-piercing bodies[J].Ocean Engineering,2007,34:1000-1012.

[7]Liao Z P.Extrapolation non reflecting boundary conditions[J].Wave Motion,1996,24:117-138.

[8]Xu G,Duan W Y.Time domain simulation for water wave radiation by floating structures(Part A)[J].Journal of Marine Science and Application,2008;7:226-235.

[9]Xu G,Duan W Y.Time-domain simulation of wave-structure interaction based on multi-transmitting formula coupled with damping zone method for radiation boundary condition[J].Applied Ocean Research,2013;42:136-143.

[10]Duan W Y,Zhang T Y.Non-reflecting simulation for fully-nonlinear irregular wave radiation[C]//Proceedings of the 24th International Workshop on Water Wave and Floating Bodies.Bodies,Russia,2009.

[11]Cao Y,Schultz W W,Beck R F.Three dimensional desingularized boundary integral methods for potential problems[J].International Journal for Numerical Methods in Fluids,1991,12:785-803.

[12]Xu G.Time-domain simulation of second-order hydrodynamic force on floating bodies in irregular waves[D].Harbin:College of Shipbuilding Engineering,Harbin Engineering University,2010.(in Chinese)

基于多次透射公式和无奇异边界元法模拟全非线性数值波浪水池

徐 刚，白 旭，马小剑，朱仁庆
（江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003）

文章基于势流理论对全非线性的三维数值水池进行了模拟，其控制方程由无奇异边界积分方程法（Desingularized Boundary Integral Equation Method,DBIEM）进行离散求解，在求解全非线性的自由面微分方程时，文中采用混合欧拉—拉格朗日法（Mixed Eulerian-Lagrangian,MEL）和四阶Adams-Bashforth-Moulton（ABM4）预报—修正方法，为了避免结果发散即增强数值稳定性，文中采用B样条法来光顺波面。同时，在远方辐射控制面上采用多次透射公式方法（Multitransmitting Formula,MTF）来进行消波，文中得到的结果与理论解进行了比较，结果表明该方法可用来有效模拟全非线性的数值波浪水池。

数值波浪水池；无奇异边界积分法；多次透射公式

O35 U661.71

A

国家自然科学基金资助项目（51309125,51409128,51379094,51179077）；江苏高校优势学科建设工程资助项目资助

徐 刚（1981-），男，博士，江苏科技大学船舶与海洋工程学院副教授；白 旭（1984-），男，博士，江苏科技大学船舶与海洋工程学院讲师；马小剑（1982-），男，博士，江苏科技大学船舶与海洋工程学院讲师；朱仁庆（1965-），男，博士，江苏科技大学船舶与海洋工程学院教授。

10.3969/j.issn.1007-7294.2017.09.002

Article ID： 1007-7294（2017）09-1062-09

Received date：2017-03-28

Foundation item:Supported by the National Natural Science Foundation of China(Grant No.51309125,51409128,51379094,51179077)and the Project Founded by Priority Academic Program Development of Jiangsu Higher Education Institutions

Biography：XU Gang(1981-),male,Ph.D.,associate prof.of Jiangsu University of Science and Technology,E-mail:me_xug@qq.com;BAI Xu(1984-),male,Ph.D.,lecturer.