主动悬架的滑模控制指数趋近率参数优化

王 健，蔡宇萌

(江苏大学 汽车与交通工程学院， 江苏 镇江 212013)

主动悬架的滑模控制指数趋近率参数优化

王 健，蔡宇萌

(江苏大学 汽车与交通工程学院， 江苏 镇江 212013)

针对车辆主动悬架滑模控制方法中按经验选取指数趋近率参数造成悬架控制效果未能达到预期的问题，提出一种滑模控制参数优化方法，消除了指数趋近率参数选取的随意性，提高了主动悬架的控制效果和控制精度。首先建立1/4车辆主动悬架系统模型，并根据滑模运动方程稳定的Hurwitz判据选择滑模面系数,使用指数趋近率改善滑模运动段的动态特性；其次分析滑模控制方法中按经验选取指数趋近率参数的缺点，并采用遗传算法对其进行优化。仿真结果显示：与被动悬架和滑模控制悬架相比，优化后的滑模控制悬架二次型性能指标分别减小了7.6%和35.6%，簧载质量加速度均方根值减小了13.3%和45.6%，表明运用遗传算法对滑模控制参数优化后的控制效果优于优化之前，证明了这种优化滑模控制方法的先进性。

主动悬架；遗传算法；滑模控制

Abstract: An improved sliding mode control method is proposed to remedy the poor control effect raised from exponent approaching sliding mode parameter randomly chosen used in vehicle active suspension. The control effect and accuracy is consequently increased. Firstly, 1/4 vehicle active suspension system model is built. Coefficient of sliding mode surface was selected in accordance with Hurwitz stable judgement of sliding mode motion equation. Exponent tendency rate was used to improve dynamic quality of sliding mode motion. Secondly, the weakness exponent approaching sliding mode parameter chosen randomly is pointed out and optimized by genetic algorithm. Finally, Results show that the suspension quadratic performance indexes of the improved sliding mode control suspension reduce by 7.6% and 35.6% compared with passive suspension and sliding mode control suspension, respectively, and the root mean square value of the sprung mass acceleration decrease 13.3% and 45.6%, respectively. The optimized control effect by genetic algorithm is much better than before and advancement of the control method is proved.

Keywords: active suspension; genetic algorithm; sliding mode control

悬架作为汽车的重要总成之一，对汽车的乘坐舒适性和行驶安全性有着重要影响。随着汽车技术和控制理论的发展，出现了性能较好的半主动和主动悬架[1-3]。汽车的主动悬架系统是在普通悬架系统中附加一个可以控制阻尼作用力的装置，由执行机构、测量系统、反馈控制系统和能源系统4部分组成。主动悬架能根据汽车的运动状态和路面状况适时地调节悬架的刚度和阻尼，让悬架系统处于最佳减振状态，使车辆在各种路面状况下都有良好的舒适性。主动悬架的关键部位是其执行机构，也就是可以调节的悬架阻尼系统，因此主动悬架具有不可比拟的优越性，受到了国内外学者的广泛关注。

最近，滑模控制方法[4-5]被用在主动悬架的控制中，实现对路面激励下隔振质量的响应及主动悬架系统在系统参数摄动下的鲁棒特性进行仿真分析。结果表明：滑模控制下主动悬架系统的隔振效果远好于被动系统,而且对外界扰动有一定的适应性,对系统参数摄动也有一定的鲁棒性[6-7]。但是这种滑模控制方法仍存在一定不足：滑模控制中切换函数系数的任意选取会造成控制效果不尽如人意，因此切换函数系数的确定就显得尤为重要。本文拟采用遗传算法[8-9]对切换函数系数进行优化，研究对比优化前后路面激励响应下主动悬架系统的鲁棒特性。

1 主动悬架系统建模

1/4车辆模型相对不太复杂，且能基本表征汽车悬架的主要运动特性。本研究采用1/4车辆模型，如图1所示。

图1 1/4车辆模型

根据牛顿第二定律可得悬架系统的运动方程：

(1)

(2)

式中：f0为下限截止频率(Hz)；G0(n0)为路面不平度系数(m3)；u为汽车行驶速度(m/s)；ω(t)为路面白噪声信号。

选取状态变量为

X=[x1,x2,x3,x4]T

系统的状态方程为

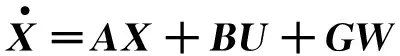
(3)

式中：

为了平衡簧载质量加速度、悬架动挠度、车轮动变形(动载荷)等悬架性能评价指标，通常采用悬架二次型性能指标J值来评价悬架系统的综合性能[10-12]。这里根据文献[13]，通过综合考虑各评价指标的主观加权比例系数与同尺度量化比例系数确定与悬架性能相关的各评价指标的加权系数。

(4)

2 滑模控制方法设计

滑模控制的切换函数表示如下：

Ss(X)=CsX=c1x1+c2x2+c3x3+x4

(5)

其中c1,c2,c3为常数。为了改善滑模运动段的动态品质,可按需规定一些趋近率。本文采用指数趋近率，表示如下：

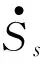
εs>0 andks>0

(6)

式中εs、ks分别为指数趋近率中sgnSs(X)和Ss(X)的系数，其中：ks决定趋近过程中到达切换面之前的速度；εs决定到达切换面时的速度。

开关函数Us表示如下：

Us=-(CB)-1[CAX+CGW+

εssgnSs(X)+ksSs(X))]

(7)

在设计滑模面时忽略式(3)中的外部扰动w,在控制律的设计中对其加以考虑。由于A、B可控,则可进行非奇异变换。

(8)

(9)

其中：

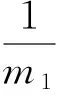
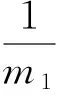
把式(8)代入式(5)中可得：

(10)

(11)

由式(11)要求：

m1-m2c3≠0

在滑模面上有：

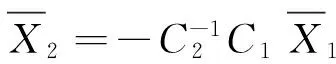
(12)

将式(12)代入式(9)得：

(13)

式(13)的特征多项式如下：

(14)

由Hurwitz稳定性判据可知：当满足

(15)

时,滑动模态稳定。

在进行控制率设计时，考虑外界扰动w，由式(3)和式(5)可得：

(16)

把式(16)代入式(6)得到滑模控制器的控制阻尼力：

Us=-(CB)-1[CAX+CGw+

εssgnSs(X)+ksSs(X)]

(17)

对于实际的减振系统,由于外界扰动w很难在线检测和估计,所以要求控制与外界扰动解耦，令扰动w的系数为0,即：

c3=0

根据式(15)得：

c1<0，c2>0,c3=0

(18)

把式(18)代入式(17)得：

Us=-(CB)-1[CAX+εssgnSs(X)+ksSs(X)]

(19)

仿真试验参数见表1。

表1 仿真试验参数

3 改进滑模控制

上述滑模控制虽然能提高车辆行驶平顺性，但仍存在一定缺陷，滑模控制中指数趋近率参数εs、ks是根据经验任意选取的，因此不能最大限度地发挥滑模控制对车辆平顺性的改进。本文拟采用遗传算法对指数趋近率参数进行优化，以提高控制效果。

遗传算法是建立在生物界遗传学的基础上、借鉴自然界生物进化机制发展起来的一种高效的全局搜索和优化方法。在搜索过程中，它模拟生物界中“物尽天择，适者生存”的规则，在全局范围内通过群体内染色体信息交换的机制，不断寻找相近的、更能适应环境的个体，即最优解。

与其他优化算法相比，遗传算法有以下特点：算法的应用领域更广泛；有更好的全局并行性；更高效。遗传算法在优化过程中，将目标函数值转化为适应度函数而直接加以利用，可以提高搜索效率。遗传算法具有内在引导性和灵活性，但作为一种优化方法，也存在一些局限性：算法编码规则不规范；算法编码对优化问题的表示不够准确；算法容易过早或局部收敛。

遗传算法在优化过程中，并不对求解变量本身的实际值进行操作，而是先对优化变量进行编码，再模拟生物进化和自然选择过程中发生的复制、交叉和变异等现象进行遗传操作，通过适应度来评价每个个体的优劣，最后在算法收敛时找到最优个体。图2为遗传算法的运算流程。

图2 遗传算法的运算流程

选取滑模控制中的指数趋近率参数εs、ks进行优化，通过初步取样计算，设定合理取值范围为：εs=[0，0.1]，ks=[0，50]。初始种群数量为100，最大遗传代数为30。交叉概率和变异概率分别取0.9和0.08，代沟取0.6。

目标函数为二次型性能指标，表示如下：

在Matlab/Simulink下搭建仿真模型，仿真时间为10 s。经优化计算得到：εs=0.023,ks=25.62。仿真结果见图3。

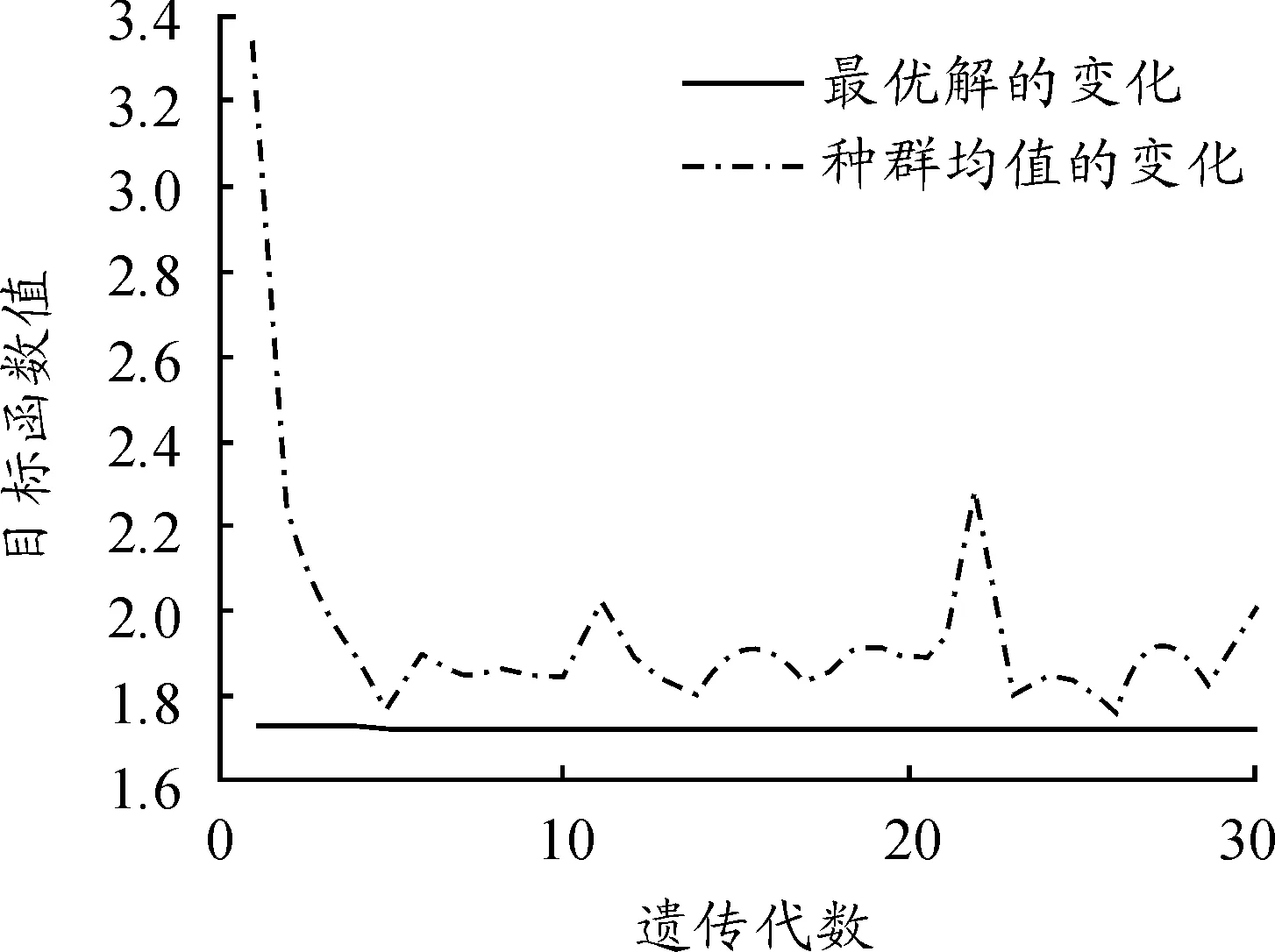
图3 种群均值和最优解的变化

由图3可知：在优化求解过程中，最优解收敛于17.204 5，种群均值有大的波动。这是由于产生了新的种群，种群的差异性产生了较大的波动，但不影响最优解的获得。

4 仿真分析

把优化得到的结果代入1/4车辆主动悬架系统模型中进行仿真。

1) 时域分析

在平顺性性能对比过程中，为了使优化滑模控制悬架与被动悬架以及滑模控制悬架能清楚地比较，通常选用垂向加速度作为悬架系统主要的性能评价指标，选取轮胎动载荷以及悬架动挠度作为辅助的性能评价指标，最后选取车辆悬架二次型性能指标J值作为评定悬架综合性能的指标[14-15]。

图4～7为优化滑模控制悬架与被动悬架以及滑模控制悬架的车辆各性能指标时域曲线比较。由图4、5及表2的仿真结果可知：优化滑模控制悬架的轮胎动载荷幅值以及悬架动挠度幅值相对被动悬架都略微增大。 由图6及表2可知：优化滑模控制悬架的垂向加速度均方根值与被动悬架相比减少45.6%,与滑模控制悬架相比减少13.3%。且由图7及表2可知：优化滑模控制悬架的悬架二次型性能指标J值与被动悬架相比减小35.6%，与滑模控制悬架相比减小了7.6%。

图4 动载荷曲线

图5 动挠度曲线

图6 垂向加速度曲线

图7 二次型性能指标J

性能指标被动悬架滑模控制优化滑模控制动载荷均方根值0.00400.00380.0048动挠度均方根值0.01450.01490.0177车身质量加速度均方根值1.90571.19471.0356悬架二次型性能指标J1.57561.09651.0135

以上仿真结果说明：采用滑模控制悬架或优化滑模控制悬架都无法保证悬架的各性能评价指标均优于被动悬架。为了获得尽可能好的悬架综合性能和减小车身质心垂向加速度幅值，需要权衡悬架各方面性能参数。本文所设计的悬架系统使车轮动载荷和悬架动扰度相对于被动悬架变差，但车身质心加速度明显减小，且具有较好的悬架综合性能，使得车辆行驶的平顺性得到了改善，提高了乘坐舒适性。

2) 频域分析

本文在时域分析中选取垂向加速度作为悬架系统性能的主要评价指标，选取轮胎动载荷以及悬架动挠度作为辅助的性能评价指标，所以需要从频域角度[16]出发对车身垂向加速度的时域信号进行功率谱密度(PSD)分析。从图8中可以看出：装载被动悬架车辆的车身质心加速度功率谱密度在低频(0～3 Hz)出现一个明显的峰值，说明在该频率下车身的振动能量分布较大，低频振动会影响乘坐舒适性。滑模控制悬架以及优化滑模控制悬架的车辆车身质心加速度功率谱密度相比于装载被动悬架的车身质心加速度功率谱密度峰值明显降低，并且装载优化滑模控制悬架的低频峰值略低于滑模控制悬架。

图8 加速度功率谱密度

5 结束语

针对在1/4车辆主动悬架滑模控制方法中指数趋近率参数的任意选取造成控制效果未能达到最优的问题，提出一种优化滑模控制方法。建立1/4车辆主动悬架系统模型，根据滑模运动方程稳定的Hurwitz判据选择滑模面系数，用指数趋近率改善滑模运动段的动态特性，并运用遗传算法对指数趋近率参数进行优化。结果表明：优化滑模控制主动悬架性能远好于被动悬架，略优于滑模控制主动悬架，提高了主动悬架的控制效果和控制精度。

[1] THOMPSON A G.An active suspension with optimal linear state feedback[J].VSD,1976(5):187-203.

[2] 喻凡，张勇超.馈能型车辆主动悬架技术[J].农业机械学报，2010，41(1)：1-6.

[3] 姚嘉伶，蔡伟义，陈宁.汽车半主动悬架系统发展状况[J].汽车工程，2006，28(3)：276-280.

[4] ANDRZEJ B,PIOTR L.Reaching law approach to the sliding mode control of periodic review inventory systems[J].IEEE Transactions on Automation Science and Engineering,2014,11(3):810-817.

[5] 姚琼荟,黄继起,吴汉松.变结构控制系统[M].重庆：重庆大学出版社,1997.

[6] LEE J H,LEE H J,SUNWOO M.Nonlinear sliding mode observer for exhaust manifold pressure estimation in a light-duty diesel engine,International[J].Journal of Automotive Technology,2014,15(3):377-386.

[7] 黄昆，喻凡，张勇超.电磁式主动悬架模型预测控制器设计[J].上海交通大学学报,2010,44(11):1619-1624.

[8] BAGLEY J D.The behavior of adaptive system which employ genetic and correlation igorithm[D].MICHIGAN:University of MICHIGAN,1976.

[9] 贝绍轶,陈龙.基于遗传算法的汽车半主动悬架模糊控制器设计[J].农业机械学报,2006,37(9):9―12.

[10] KARIMI Hamid-reza.Robust delay-dependentH∞control of uncertain time-delay systems with mixed neutral,discrete,and distributed time-delays and Markovian switching parameters[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2011,58(8):1910-1923.

[11] YANG J N,WU J C,LI Z.Control of seismic-excited buildings using active variable stiffness systems[J].Engineering Structures,1996,18(8):589-596.

[12] 郑玲，邓兆祥，李以农.汽车半主动悬架的模型参考自适应控制[J].中国公路学报,2005,18(2):99-102.

[13] 陈士安，邱峰，何仁，等.一种确定车辆悬架LQG控制加权系数的方法[J].振动与冲击，2008，27(2)：65-68.

[14] 朱华.车辆半主动悬架联合仿真研究[J].机械设计与制造，2010，12：205-207.

[15] CHENG C,CEBON D.Improving roll stability of articulated heavy vehicles usingactive semi-trailer steering[J].Vehicle System Dynamics,2008,46(S1):373-388.

[16] SHIM T,TOOMEY D,GHIKE C,et al.Vehicle rollover recovery using activesteering/wheel torque control[J].International Journal of Vehicle Design,2008,46(1):51-71.

(责任编辑陈 艳)

ParameterOptimizationofExponentApproachingSlidingModeControlMethodforActiveSuspension

WANG Jian, CAI Yumeng

(School of Automotive and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)

2016-11-08

国家自然科学基金资助项目(1721122043)

王健(1992—)，男，江苏常州人，硕士研究生，主要从事主动/半主动悬架控制技术方面的研究，E-mail:912378048@qq.com。

王健，蔡宇萌.主动悬架的滑模控制指数趋近率参数优化[J].重庆理工大学学报(自然科学)，2017(9):15-21.

formatWANG Jian, CAI Yumeng.Parameter Optimization of Exponent Approaching Sliding Mode Control Method for Active Suspension[J].Journal of Chongqing University of Technology(Natural Science)，2017(9):15-21.

10.3969/j.issn.1674-8425(z).2017.09.003

TH16；U463.33

A

1674-8425(2017)09-0015-07