公司特质风险、估值水平与股票收益——基于分位数Fama-MacBeth回归模型的实证分析

赵胜民，刘笑天

（南开大学 金融学院，天津 300350）

●本期视点

公司特质风险、估值水平与股票收益
——基于分位数Fama-MacBeth回归模型的实证分析

赵胜民，刘笑天

（南开大学 金融学院，天津 300350）

文章建立理论模型探究公司特质风险、估值水平与股票收益之间的关系，理论模型结果表明：对于被低估的公司，特质风险的私有信息效应更加明显，股票预期收益率与特质风险之间呈正相关关系；对于被高估的公司，特质风险的噪声交易效应更加明显，股票预期收益率与特质风险之间呈负相关关系。在此基础上，从公司估值水平和卖空限制的角度对整体市场的特质波动率之谜进行了理论解释。文章使用Fama-French五因子模型计算特质风险和估值水平，运用分组检验和分位数Fama-MacBeth回归两种方法进行实证分析，基于我国上市公司数据的实证研究结果支持了理论模型的结论：中国股票市场存在明显的特质波动率之谜，公司估值水平会对特质风险与股票预期回报之间的关系产生影响。

特质风险；估值水平；私有信息；噪声交易

一、引 言

公司的特质风险是否会影响股票的预期收益率？这个问题一直是学术界的争论焦点。作为特质风险的度量，特质波动率其与预期收益率的关系一直饱受争议。经典金融理论认为特质风险可以通过分散化投资的手段进行规避，因此不会影响预期收益率。然而经典金融理论中关于理想市场的假设过于完美，现实中投资者会面临交易成本、卖空限制、信息不对称等交易壁垒，Merton（1987）［1］认为投资者会由于不能充分分散股票的特质风险而要求更高的风险补偿，并从理论层面证明了预期收益率与特质风险之间的正相关关系。然而Ang等（2006，2009）［2-3］在实证检验的基础上发现了股票预期收益率与特质波动率之间存在负相关的关系，这既不被经典金融理论所支持，又不能被Merton的模型所解释，因此学术界将预期收益率与特质波动率之间的负相关关系称为“特质波动率之谜”。

学术界对于公司特质风险的界定存在两种观点：一是信息论［4］，即特质风险代表着公司的私有信息，特质风险较高的公司有着更大的发展潜力与更广阔的发展前景，因此投资者承担额外的特质风险会要求更高的风险补偿；二是噪声论［5］，即特质风险代表着投资者的噪声交易行为，公司的特质波动并不能体现私有信息，特质风险越高的股票对应的错误定价风险也越高。本文认为公司的估值水平不同，特质风险的主要表征形式也不同，因此特质风险对股票预期收益率的影响也会发生变化，基于公司估值水平角度的分析有助于我们更好地理解资本市场中普遍存在的特质波动率之谜。

本文利用Fama-French五因子模型［6］提取特质波动率作为公司特质风险的度量，在横截面回归的基础上求解股票已实现的异常收益率作为公司估值水平的度量。这里我们认为股票收益率中能被Fa⁃ma-French五因子模型的风险定价因子解释的部分代表股票的期望收益率，因此多因子回归模型的常数项，即异常收益率能够在一定程度上刻画公司的估值水平。我们建立了理论模型探究公司特质风险、估值水平与股票收益之间的关系，理论模型的结果表明：对于被高估的公司，特质风险的噪声交易效应更加明显，因此特质风险与预期收益率呈负相关关系；而对于被低估的公司，特质风险的私有信息效应更加明显，因此特质风险与预期收益率呈正相关关系。在此基础上，我们从公司估值水平和卖空限制的角度对整体市场的特质波动率之谜进行了理论解释。基于分组检验和分位数Fama-MacBeth回归方法的实证研究结果支持了理论模型的结论：中国股票市场存在明显的特质波动率之谜，公司的估值水平不同，其预期收益率与特质波动率之间的关系也不同。

相比以往的研究，本文的创新点主要有三方面：一是使用最新的Fama-French五因子模型作为基准定价模型进行分析计算，以特质波动率度量特质风险、以异常收益率度量估值水平，并与三因子模型的结果进行对比，在对理论模型进行实证检验的同时，也探究了特质波动率提取方式对特质波动率之谜的影响。二是构建了公司特质风险、估值水平与股票预期回报率之间的理论模型，从估值水平的角度对私有信息效应和噪声交易效应进行区分，指出公司特质风险与股票预期回报之间的关系受到估值水平的影响。三是创造性地从估值水平与卖空限制的角度对特质波动率之谜进行理论解释，丰富了特质波动率之谜相关领域的研究体系，并为上市公司的风险管理和投资者的交易决策提供了有价值的参考。

二、文献综述

国外学者在特质波动率方向进行了丰富的研究，这里先从特质波动率的求解方式、特质波动率与预期收益率之间的关系和对特质波动率之谜的解释三个方面对国外文献进行梳理，最后对国内的相关研究进行总结。

（一）特质波动率的求解方式

准确地测度特质波动率是研究“特质波动率之谜”的首要前提，不同学者从不同角度给出了特质波动率的度量方法。Campbell等（2001）［7］在假设市场超额收益与个股超额收益不相关的前提下，直接从个股收益率中将市场收益率分离来计算特质波动率。这种方法虽然计算简便，但是市场收益并不能完全反映股票的系统性风险溢价，因此不能准确地刻画个股的特质波动率。此后的研究大多从市场定价模型的角度计算股票的特质波动率。

Tinic和West（1986）［8］采用CAPM模型对股票收益率进行回归，以残差序列的标准差来刻画特质波动率。Ang等（2006）将个股的特质波动率定义为最近一个月内日收益率偏离每日基准调整收益率的标准差，这里的基准调整收益率以Fama-French三因子来刻画：MKT，SMB和HML。即在每个月内对个每只股票进行Fama-French三因子回归，以残差项的标准差作为个股当月的特质波动率。

不同于以市场定价模型的残差标准差来定义特质波动率，一些学者从时间序列分析的角度来定义和估计预期的特质波动率。Fu（2009）［9］发现特质波动率具有时变性和非对称性，提出了以EGARCH模型来估计特质波动率；Huang等（2010）［10］以ARIMA模型来度量预期特质波动率。

Jin（2013）［11］对以上不同的特质波动率提取方法进行了对比分析，肯定了从市场定价模型角度定义的特质波动率的优势，指出基于市场定价模型计算特质波动率要优于GARCH和EGARCH模型估计的结果。由此可见，根据多因子定价模型计算特质波动率，是目前学术界公认的求解特质波动率较好的方式。

（二）特质波动率与预期收益率之间的关系

学术界对于特质波动率与预期收益率之间的关系一直存在很大争议。在Merton（1987）从理论上证明了预期收益率与特质波动率之间存在正相关关系之后，许多学者在实证检验中得到了正相关的结论。Ticnic和West（1986）在实证检验中发现了特质波动率与预期收益率的正相关关系。Xu和Malkiel（2003）［12］用Fama-French三因子模型提取特质波动率，在实证检验中也发现了显著的正相关关系。

而Ang等（2006）在实证检验中发现了负相关的关系，并指出之前关于正相关关系的实证存在一定的问题，它们有些没有在个股水平上检验特质波动率与预期收益率的关系，还有些在进行分组时没有直接以特质波动率为依据。此后，越来越多的学者在实证研究中得到负相关的结论。Jiang（2009）［13］、Guo和Savickas（2010）［14］分别以美国股票市场中不同时期的数据为样本检验了Ang（2006）的结论，发现了负相关关系的存在。Ang等（2009）对23个发达国家的资本市场数据进行实证检验，研究发现股票预期收益率与特质波动率之间的负相关关系是稳健的。

最近的一个得到正相关结论的研究来自Fu（2009）的文章，但是 Fink，Fink和 He（2012）［15］以及Guo，Kassa和Ferguson（2014）［16］指出Fu（2009）中正相关的结论是由于使用了条件方差模型中同时期的信息，如果对这部分信息加以控制，将不会出现正相关的结论。至此，越来越多的研究证实了特质波动率之谜的存在，整体市场中特质波动率与预期收益率之间存在负相关关系的观点逐渐占据主导地位。

同时，也有一些学者指出预期收益率与特质波动率之间的正负相关关系同时存在。Stambaugh，Yu和Yuan（2015）［17］综合运用了11种市场异象指标来判断股票价格所处的状态，并指出对于高估状态的股票，预期收益率与特质波动率负相关，而对于低估状态的股票，预期收益率与特质波动率正相关。Rach⁃walski和Wen（2016）［18］研究发现，短期内预期收益率与近期的特质波动率负相关，而在长期水平上预期收益率与特质波动率正相关。这一现象提示我们，虽然就整体市场而言特质波动率之谜存在，但是在整体的不同部分中特质波动率与预期收益率可能存在不同的关系。

（三）特质波动率之谜的解释

许多学者从投资者博彩偏好（Lottery Preference）的角度给出解释。Baberis和Huang（2008）［19］指出在累积前景理论的框架下，投资者会高估小概率事件发生的概率，偏好具有正偏度的股票，导致这部分股票的价格被高估，这将有助于解释特质波动率之谜。随后Boyer，Mitton 和 Vorkink（2010）［20］利用预期的特质偏度对特质波动率之谜作出了合理的解释。此外，Bali，Cakici和 Whitelaw（2011）［21］从历史最大日收益率的角度解释了特质波动率之谜，Han和Kumar（2013）［22］认为股票中的散户交易比例也能解释特质波动率之谜。

也有一些学者从市场限制的角度来解释特质波动率之谜。Huang等（2010）指出由于市场微观结构的偏差，股票在每个月内具有明显的价值反转效应，在对其进行控制后，特质波动率之谜变得不再显著。Han和Lesmond（2011）［23］以每个月内零收益率天数来测度非流动性，同时指出买卖价差也会影响特质波动率之谜。Boehme等（2009）［24］以及Duan，Hu和McLean（2010）［25］探讨了卖空限制对特质波动率之谜的影响，指出对于卖空限制很高的股票，负相关关系明显，而对于卖空限制很低的股票，负相关关系很弱甚至消失。

此外，还有一些学者从其他角度分析特质波动率之谜的成因。Johnson（2004）［26］运用分析师分歧程度来表征基本面信息的不确定性，Chen和Petkova（2012）［27］对市场方差进行分解，定义了平均方差贝塔的概念，都能在一定程度上解释特质波动率之谜。

（四）国内的相关研究

国内学者利用中国股票市场的数据，对特质波动率之谜进行了研究。由于样本选择、特质波动率求解方式等差异，研究结论不尽相同。一些学者支持正相关的结论，邓雪春和郑振龙（2011）［28］利用ARIMA模型提取预期特质波动率，发现了预期收益率与预期特质波动率之间存在着正向关系。罗登跃（2013）［29］在实证研究中发现，已实现特质波动率和非预期特质波动率均与收益显著正相关。熊伟和陈浪南（2015）［30］发现股票特质波动率与收益率正相关，且这种正相关关系会随着投资者情绪的增加而增加。

一些学者支持负相关的结论，徐小君（2010）［31］运用包含市场风险因子和偏度风险因子的两因子定价模型来度量特质波动率，发现了特质波动率与预期收益率呈显著的负相关关系。杨华蔚和韩立岩（2011）［32］建立了基于投资者异质信念的消费资本资产定价模型，并从异质信念和外部风险的角度对特质波动率之谜进行了理论解释。左浩苗等（2011）［33］发现股票特质波动率与横截面收益率存在显著的负相关关系，但在控制了表征异质信念的换手率后，这种负相关关系便消失了，因此作者认为是卖空限制和投资者的异质性造成了特质波动率之谜。黄卓等（2015）［34］在实证研究中也发现二者之间存在显著的负相关关系，并分析了股权分置改革对特质波动率之谜造成的影响。

还有一些学者给出了正负相关关系同时存在的证据。张宇飞和马明（2013）［35］发现了预期收益率与特质波动率之间的负相关关系，但在控制了一些表征投资者意见分歧的代理变量后，这种关系转变为正相关关系。李竹薇等（2014）［36］基于HP滤波法将特质波动率分解为长期特质波动率和短期特质波动率，进一步研究发现长期特质波动率与股票横截面收益成正向关系，短期特质波动率与股票横截面收益成反向关系。

此前的关于特质风险与预期收益率的研究，大多基于Fama-French三因子模型，而且国内学者对于预期收益率与特质波动率之间的关系存在很大争议。基于此，本文在Fama-French五因子模型的框架下，对我国股票市场中预期收益率与特质波动率之间的关系进行实证检验。

三、理论模型

在一个没有卖空限制和交易摩擦的完美市场中有N个风险资产，它们在整个市场中的分布向量用y表示。市场中存在两种类型的投资者，理性交易者和噪声交易者，假设噪声交易者对N个风险资产的需求外生给定，用N维列向量yn表示，理性交易者所拥有的全部资本为YR，他们通过最优化的目标函数来决定风险资产的权重配置，即

其中，R是N个风险资产的期望收益率向量；ω是在每种资产上的权重分配向量；V是N个风险资产收益率的方差协方差矩阵；A为风险厌恶系数，假设每种风险资产的期望收益率服从下面的多因子定价模型：

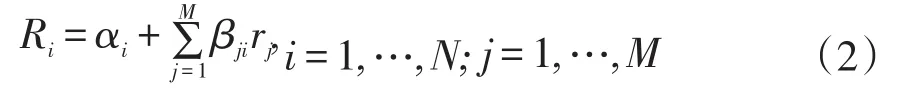
其中，rj为M个风险定价因子在当期的风险溢价，βji为第i个风险资产关于第j个风险定价因子的beta系数，αi为第i个风险资产的异常收益率，即其收益率中不能被其他风险定价因子所解释的部分。假设风险资产收益率的方差协方差矩阵V具有如下形式：其中，σj

2为第j个风险定价因子的收益率的方差；βj为全部风险资产关于第j个风险定价因子的beta系数构成的N维列向量；Σ是一个N阶对角矩阵，它的对角线上的元素依次为N个风险资产的异常收益率的方差，即特质波动率的平方。

理性投资者的最优权重分配向量记为ωR，因此市场均衡时满足：

定义噪声交易者对第i个风险资产的超额需求为yεi，满足：

定理1：市场均衡状态下，对于第i个风险资产，其异常收益率αi与特质波动率σεi2存在如下关系：

证明：在没有卖空限制和交易摩擦的完美市场中，理性投资者的最优投资权重满足下面的一阶条件：

这里的一阶条件不仅适用于每种风险资产，对每个风险定价因子同样成立，即

将（7）式的最优权重带入市场均衡条件（4），有

由于市场组合中每个风险定价因子的beta系数的市值加权平均值为1，即

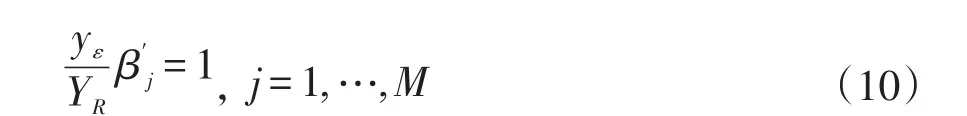
因此，对于每一个风险资产，其异常收益率可以表示成如下形式：

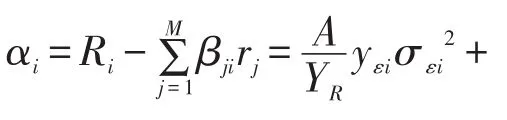
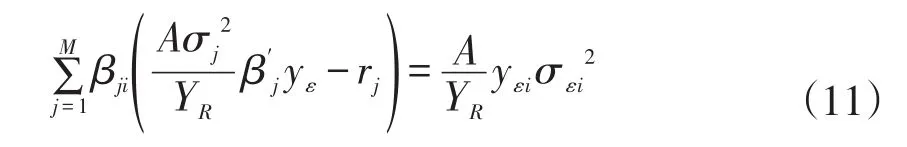
证毕。

定理1的结论表明，当公司处于被低估的状态时，其超额需求为正，yεi＞0，因此股票收益率与特质风险呈正相关关系；当公司处于被高估的状态时，其超额需求为负，yεi＜0，因此股票收益率与特质风险呈负相关关系。我们可以从特质风险的来源形式角度对这一结果进行说明：由于被低估股票的噪声交易者参与程度相对较低，公司特质风险主要来源于私有信息，特质风险的私有信息效应更加明显，此时特质风险代表了公司的未来发展潜力与投资前景，特质风险较高的公司其发展潜力也较高，因此，根据经典资产定价理论，风险与收益总是相匹配的，投资者在承担额外的风险时会要求更高的风险溢价作为补偿，对于被低估状态的公司而言，股票的预期回报与特质风险正相关；而当股票处于被高估的状态时，噪声交易者的盲目跟风等羊群行为会更加明显，市场参与度相对较高，公司的特质风险主要来源于噪声交易行为，其噪声交易效应更为明显，特质风险并不能体现公司的私有信息，承担这部分风险并不会获得额外的风险补偿，而噪声交易者的行为会使股票的当期价格进一步脱离其内在价值，因此股票的预期回报与特质风险将呈现负相关关系。

理论模型的结论表明，公司估值水平的高低对于特质波动率之谜具有重要影响。鉴于Ang等（2009）在全球多个资本的实证检验中发现了显著的特质波动率之谜，在理论模型的基础上，我们可以对整体市场的特质波动率之谜进行解释。高特质波动率代表着高套利风险，这部分股票的套利交易修正价格机制很难发挥作用，因此高特质波动率的股票更容易被错误定价。由于市场中存在着卖空限制等约束，会导致套利的非对称性（Stambaugh等，2015），做多比做空更加容易，因此被低估公司股票的错误定价相比被高估公司股票更容易被套利者消除。所以，从整体市场来看，处于被高估状态的股票的特质波动率与预期收益率之间的关系占据主导地位，即被高估股票的噪声交易效应所导致的负相关关系要强于被低估股票的私有信息效应所导致的正相关关系，因此股票市场就会出现特质波动率之谜，即预期收益率与特质波动率呈负相关关系。

四、实证分析

（一）数据来源与变量定义

本文以中国沪深两市全部A股（包括中小板和创业板）作为实证研究对象，样本期选择从2000年1月4日到2015年12月31日。股票的交易数据和财务数据来自Wind金融数据库，无风险收益率数据来自锐思金融研究数据库。

数据选取及处理如下：①选取每年交易数据和财务数据都完整的股票计算Fama-French五因子数据，财务数据的选取标准同赵胜民等（2016）［37］，分组方式采用2×3的模型；②为保证每个月内有足够的数据进行个股的Fama-French五因子回归，我们剔除了当月交易天数小于10天的数据；③在进行分组检验和Fama-MacBeth回归检验时，如果某一时间截面没有数据，在取平均时予以剔除。

本文的实证检验采用Fama-MacBeth回归的方法，在每个时间截面上，被解释变量为月度收益率（前复权），核心解释变量为特质波动率（IVOL）和异常收益率（Alpha），分别作为特质风险和估值水平的代理变量，具体计算方法如下：

（1）IVOL：以Fama-French五因子模型为市场定价模型，将个股每个月内日收益率数据与对应的五因子日数据进行回归，具体而言，在第t月内，将股票i的收益率日数据进行下面的回归。

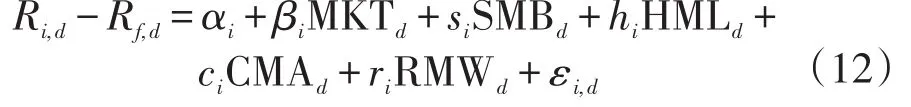
其中，Ri,d-Rf,d为股票i在第t月第d天的超额收益率，MKTd、SMBd、HMLd、CMAd、RMWd为对应的 Fama-French五因子的值，股票i在第t月的特质波动率值为当月内回归方程残差项的标准差。

特别地，我们也使用Fama-French三因子模型提取了股票的特质波动率，为了进行对比区分，将五因子模型计算得到的特质波动率记为IVOL_FF5，将三因子模型计算得到的特质波动率记为IVOL_FF3。

（2）Alpha：假定投资者将股票收益率中能够被五因子模型所解释的部分作为股票的内在价值，我们可以将回归式（12）中的常数项（五因子基准调整收益率）作为股票的异常收益率。

代表真实收益率与模型基准收益率的差值，刻画了股票的市场价格与其内在价值之间的偏离程度。具体而言，对于高异常收益率的股票，其价格往往处于被低估的状态；而对于低异常收益率的股票，其价格往往处于被高估的状态。

此外，许多学者在实证研究中也发现了影响股票横截面收益率的其他变量，本文选择对数流通市值（Size）、账面市值比（BM）、换手率（Turnover）、动量（MOM）、偏度（Skew）作为控制变量，特别地，对于某只股票，其第t月的动量定义为第t-2月到第t-12月的累计收益率，第t月的偏度定义为过去5年的月度收益率的偏度。全部变量的描述性统计结果见表1所列。

表1 变量的描述性统计

（二）分组样本特质波动率之谜的实证检验

我们利用分组检验和分位数Fama-MacBeth回归的方法对分组样本的特质波动率之谜进行实证检验，以探究股票估值水平的高低对特质波动率与预期收益率之间的关系的影响。首先采用分组检验的方法，在每个时间截面上按照异常收益率从小到大的顺序将股票分成5组，选择异常收益率最低（Low Alpha）和最高（High Alpha）的两个子样本进行研究。对于每个子样本，同样在每个时间截面上按照特质波动率从小到大的顺序将样本分成5组，统计每个组合的加权平均预期收益率以及最高特质波动率组与最低特质波动率组的预期收益率之差，然后对所有时间截面取平均，具体结果见表2所列。

表2 分组样本特质波动率之谜的分组检验

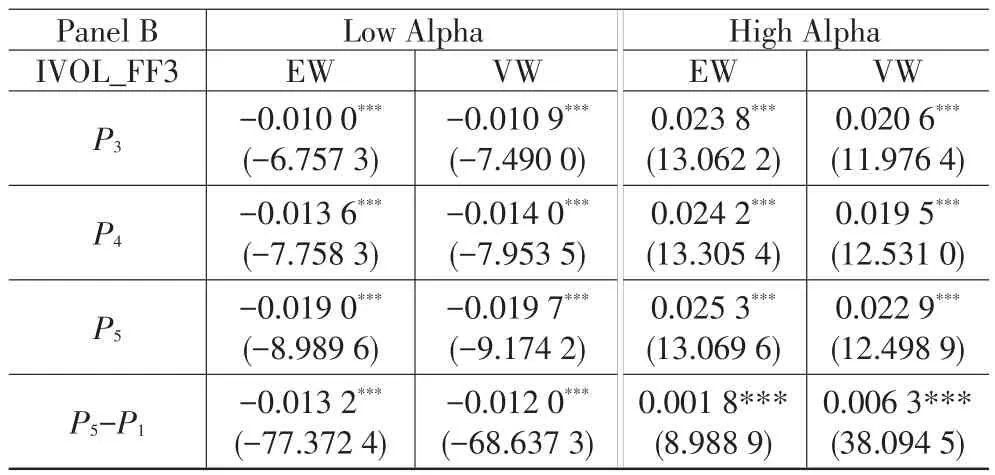
续表2

从表2的结果可见，无论使用三因子模型特质波动率还是五因子模型特质波动率、使用市值加权平均还是等权重平均，在低异常收益率（Low Alpha）样本中，最高特质波动率组合与最低特质波动率组合的预期收益率之差显著为负；而在高异常收益率（Low Alpha）样本中，最高特质波动率组合与最低特质波动率组合的预期收益率之差显著为正。这一结果较好地支持了理论模型的结论，即对于被高估公司的股票，特质风险更多体现噪声交易效应，预期收益率与特质波动率负相关，而对于被低估公司的股票，特质风险更多体现私有信息效应，预期收益率与特质波动率正相关。

进一步，本文使用分位数Fama-MacBeth回归的方法在个股水平上对异常收益率与特质波动之谜的关系进行检验。传统的Fama-MacBeth回归一共分为两步：第一步，以第t+1月的收益率为因变量，以第t月的特质波动率及其他控制变量为自变量，对所有股票在每个时期进行横截面回归；第二步，提取回归系数的时间序列，检验平均回归系数是否显著不等于0。在传统Fama-MacBeth回归的基础上，借鉴Mashruwala（2006）［38］的方法，我们将全部解释变量进行规模化处理，即对于每一个解释变量，根据它所在的分位数组将其映射到[ ]-0.5,0.5的区间上，使用分位数Fama-MacBeth回归模型进行实证分析。分位数回归模型中的变量进行映射处理有三个好处：一是可以避免异常值对回归结果的潜在影响；二是使得不同变量之间的回归系数具有可比性；三是处理后变量的回归系数有更丰富的经济意义，以特质波动率为例，其回归系数可以看作买入最高特质波动率组合、卖空最低特质波动率组合的自融资策略的预期收益率。同时，为了捕捉处于不同状态的股票（异常收益率的高低）的特质波动率与预期收益率的关系，并比较其关系的强弱，我们构造了两个虚拟变量加入Fama-MacBeth回归，在每个时间截面上，以第t+1月的收益率为因变量，以第t月的特质波动率与虚拟变量乘积项和其他控制变量（流通市值、账面市值比、换手率、动量效应、偏度效应）为自变量进行回归，其中两个虚拟变量的定义如下：如果股票i在第t+1月的异常收益率位于最低的20%，则LAi,t+1等于1，其他情况下为0；如果股票i在第t+1月的异常收益率位于最高的20%，则HAi,t+1等于1，其他情况下为0。我们用上标ran表示映射后的变量，具体的回归式见式（15）。

分位数Fama-MacBeth回归检验的具体结果见表3所列。

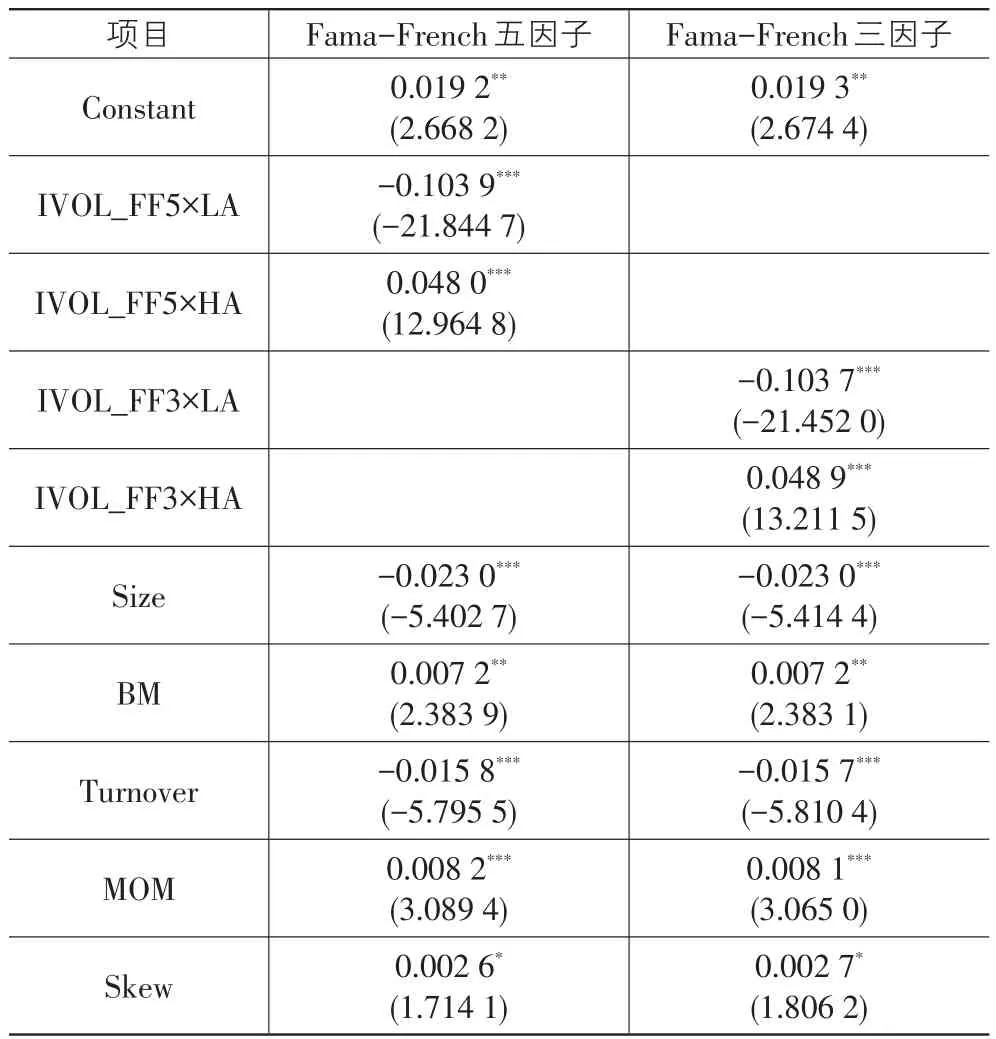
表3 分组样本特质波动率之谜的分位数Fama-MacBeth回归

表3的结果表明，使用五因子模型特质波动率时：IVOL_FF5×LA项的回归系数为-0.103 9，IVOL_FF5×HA项的回归系数为0.048；使用三因子模型特质波动率时：IVOL_FF3×LA项的回归系数为-0.103 7，IVOL_FF3×HA项的回归系数为0.048 9。个股水平实证检验的结果仍然支持理论模型的结论，即对于不同估值状态的股票，其预期收益率与特质波动率的关系不同：对于异常收益率低的股票，特质风险更多体现了噪声交易效应，预期收益率与特质波动率负相关；对于异常收益率高的股票，特质风险更多体现了私有信息效应，预期收益率与特质波动率正相关。此外，我们发现无论使用哪种模型计算特质波动率，IVOL×LA项的系数的绝对值都要大于IVOL×HA项，这在一定程度上说明了源于噪声交易效应的负相关关系的强度要高于源于私有信息效应的正相关关系，即整体市场上负相关的关系将会占主导地位。

（三）整体市场特质波动率之谜的实证检验

我们同样采用分组检验和分位数Fama-MacBeth回归的方法从两个角度对整体市场的特质波动率之谜进行检验。其中分组检验的方法如下：在第t-1月，按照股票的特质波动率由低到高的顺序将股票分成五组（P1-P5），计算每个组合在第t月的加权平均收益率，然后对所有月份的结果取算术平均，最后计算高特质波动率组合与低特质波动率组合的平均收益率之差。表4给出了不同的特质波动率计算方法（三因子与五因子）和不同的组内加权方式（市值权重与等权重）对应的计算结果。

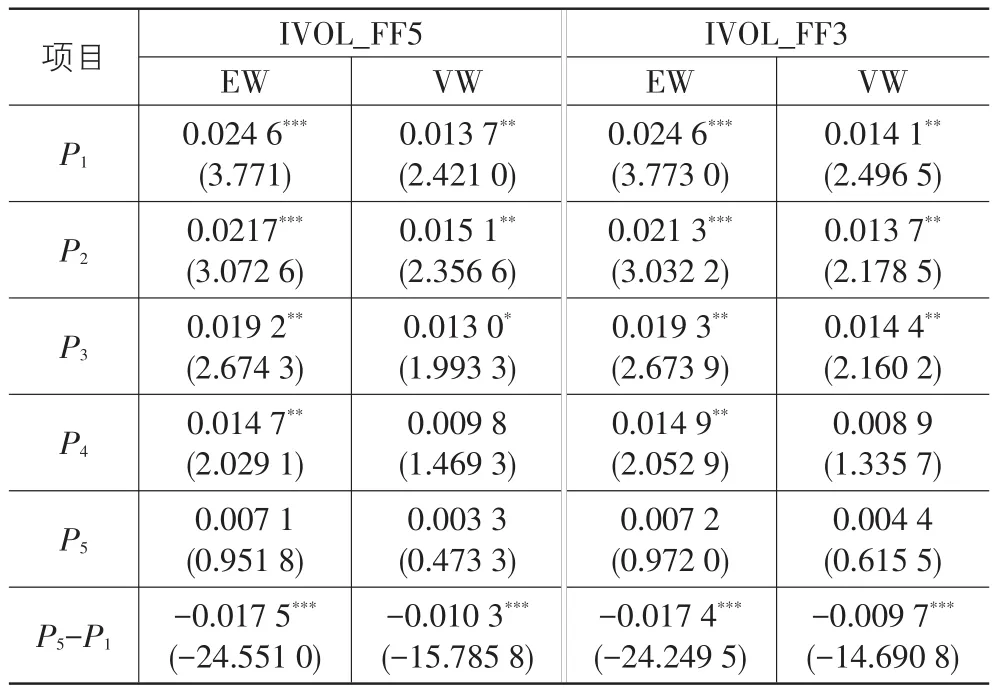
表4 整体市场特质波动率之谜的分组检验

我们发现，无论选择五因子模型计算特质波动率还是三因子模型计算特质波动率，在等权重的条件下组合的加权平均预期收益率会随着特质波动率的增加而不断减小，而在市值权重的条件下，除了五因子模型的P2组和三因子模型的P3组略有上升外，组合加权平均预期收益率也会随着特质波动率的增加而减小。整体来看，使用五因子模型计算特质波动率时，等权重条件下最高特质波动率组合与最低特质波动率组合的预期收益率差为-1.75%，在市值权重条件下二者的差为-1.03%；使用三因子模型计算特质波动率时，等权重条件下最高特质波动率组合与最低特质波动率组合的预期收益率差为-1.74%，在市值权重条件下二者的差为-0.97%。这说明使用不同的多因子定价模型计算特质波动率时，高低特质波动率组合的预期收益率之差基本不发生改变，即特质波动率之谜的存在对定价模型的选择并不敏感。同时，无论我们选择哪种模型，最高特质波动率组合与最低特质波动率组合的预期收益率之差显著为负，而且这种差异在等权重的情形下更加明显，分组检验的结果从整体市场角度说明了我国股票市场存在特质波动率之谜。

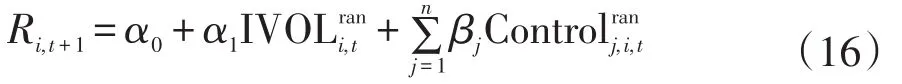
前面的研究通过分组检验的方式指出了特质波动率之谜的存在，即从整体市场水平来看，特质波动率越高，预期收益率越低。下面我们使用分位数Fama-Mac⁃Beth回归的方法从个股水平上对特质波动率与预期收益率之间关系进行检验，回归式的具体形式如式（16）。其中，Ri,t+1为股票i在第t+1月的收益率为对应的特质波动率规模化处理后的变量为对应的第j个控制变量规模化处理后的变量。同样，我们用三因子与五因子两种不同的模型计算得到的特质波动率作为解释变量，对特质波动率之谜进行Fama-MacBeth回归检验，结果见表5所列。

表5 整体市场特质波动率之谜的分位数Fama-MacBeth回归

表5结果表明，在加入了影响横截面收益率的其他控制变量后，个股水平上的检验依然支持负相关的结论：五因子模型中特质波动率的回归系数为-0.010 3，三因子模型中特质波动率的回归系数为-0.01，我国股票市场上存在着显著的特质波动率之谜。我们发现两种特质波动率的回归结果十分接近，这说明即使我们找到了更多的风险定价因子来捕捉系统性风险，特质波动率与预期收益率之间的负相关关系依然不发生改变。此外，控制变量的回归系数同样有着丰富的经济意义：对数流通市值的回归系数显著为负，说明我国股票市场的规模效应明显，小市值股票的预期回报率高于大市值股票的预期回报率；账面市值比的回归系数显著为正，表明我国股票市场的价值效应明显，价值股的预期收益率高于成长股的预期收益率；换手率的回归系数显著为负，说明换手率低的股票相比与换手率高的股票有更高的预期收益率；动量效应的系数显著为正，说明我国股票市场存在着动量效应，过去一段时间表现好的股票未来也会有更好的表现；偏度系数的回归系数并不显著，说明股票已实现的偏度对预期收益率的影响并不明显。

由于在实证检验中我们使用了规模化处理的变量，因此解释变量的回归系数之间具有可比性。以五因子模型为例，在每个月买入特质波动率最低的10%的股票、卖空特质波动率最高的10%的股票，可以获得1.03%的月平均收益率。而使用市值构建多空自融资策略可以获得2.42%的月平均收益率，使用BM构建多空自融资策略可以获得0.77%的月平均收益率，使用换手率构建多空自融资策略可以获得1.77%的月平均收益率，使用动量构建多空自融资策略可以获得0.80%的月平均收益率。我们发现，使用特质波动率构建多空自融资策略的收益率甚至超过了价值策略和惯性策略。

值得一提的是，左浩苗等（2011）在实证研究也发现了特质波动率与预期收益率的负相关关系，但在加入了换手率作为控制变量后，特质波动率之谜便消失了。由于样本选择、特质波动率计算方法存在差异，我们的实证检验结果并不支持这一结论，可以看出在加入包括换手率在内的众多控制变量的基础上，特质波动率与预期收益率的负相关关系依然显著。

五、稳健性检验

（一）变量替换

本文的实证分析分别采用了Fama-French三因子模型和五因子模型计算公司的特质风险，实证分析结果表明研究结论不发生改变，此外，我们也采用了CAPM模型和加入动量效应的四因子模型计算了特质风险，结论依然稳健，公司特质风险、估值水平与股票预期回报之间的关系并不受到特质风险计算方式的影响。

（二）样本划分

前文的实证研究对象是全部A股，国内关于股票市场横截面收益率差异的实证检验大多选择主板市场作为研究样本，这里我们以主板市场作为研究对象（剔除中小板和创业板），重复前面的实证检验过程，主要回归结果见表6所列。

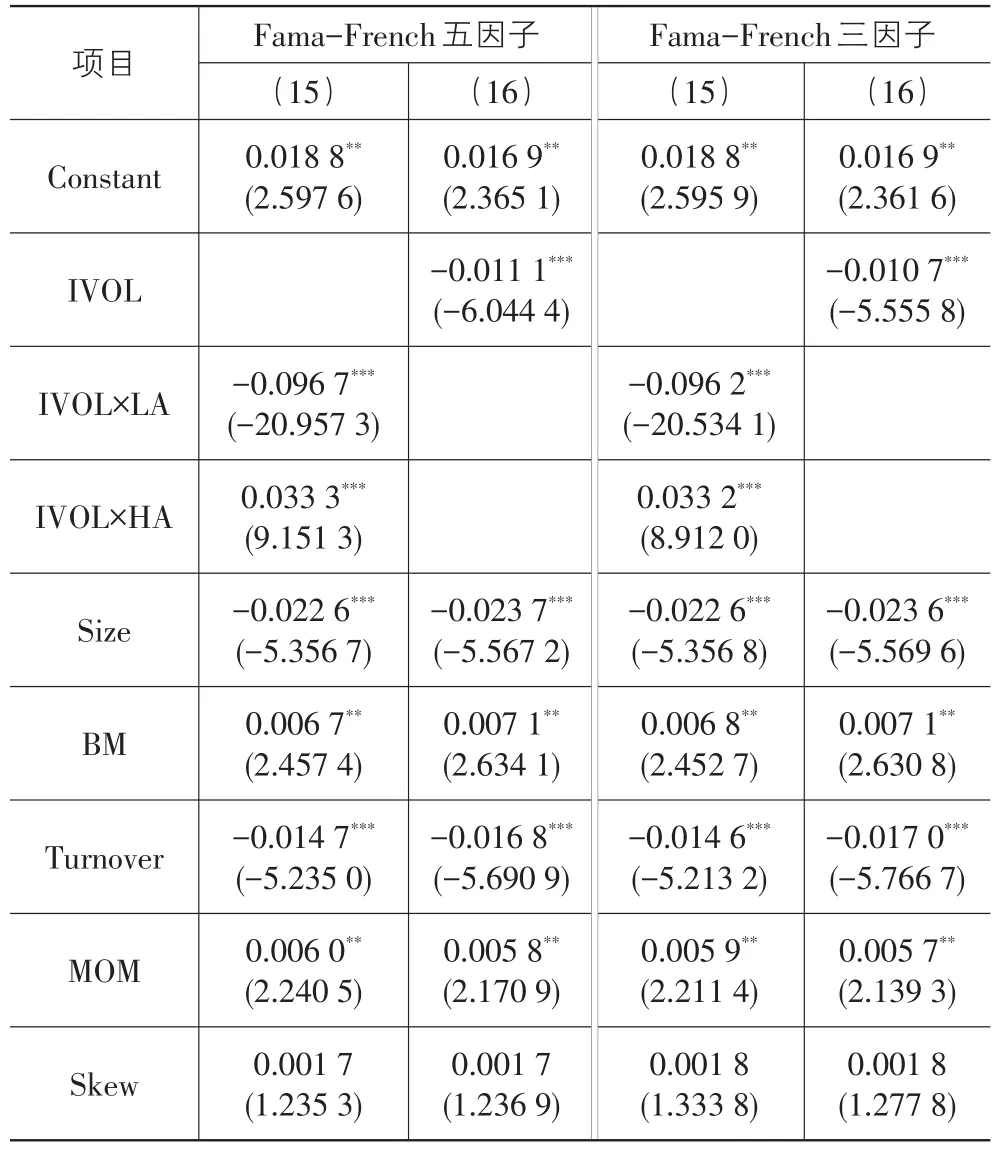
表6 主板市场的实证检验

表6结果表明，以主板市场为样本的研究并不会改变前文的结论：整体市场的特质波动率之谜依然显著，对于价值被相对高估的公司股票，其预期收益率与特质波动率负相关，而对于价值被相对低估的公司股票，其预期收益率与特质波动率正相关。

（三）计量方法

前文的实证分析主要采用分组检验和Fama-MacBeth回归检验两种方法，为证明结论的稳健性，下面使用个体时间双固定效应的面板模型对整体市场的特质波动率之谜进行检验，使用个体固定效应面板模型考察异常收益率对特质波动率之谜的影响（由于在每个时间截面都会基于异常收益率的大小关系构造虚拟变量，因此不再需要加入时间虚拟变量），具体结果如表7所列。

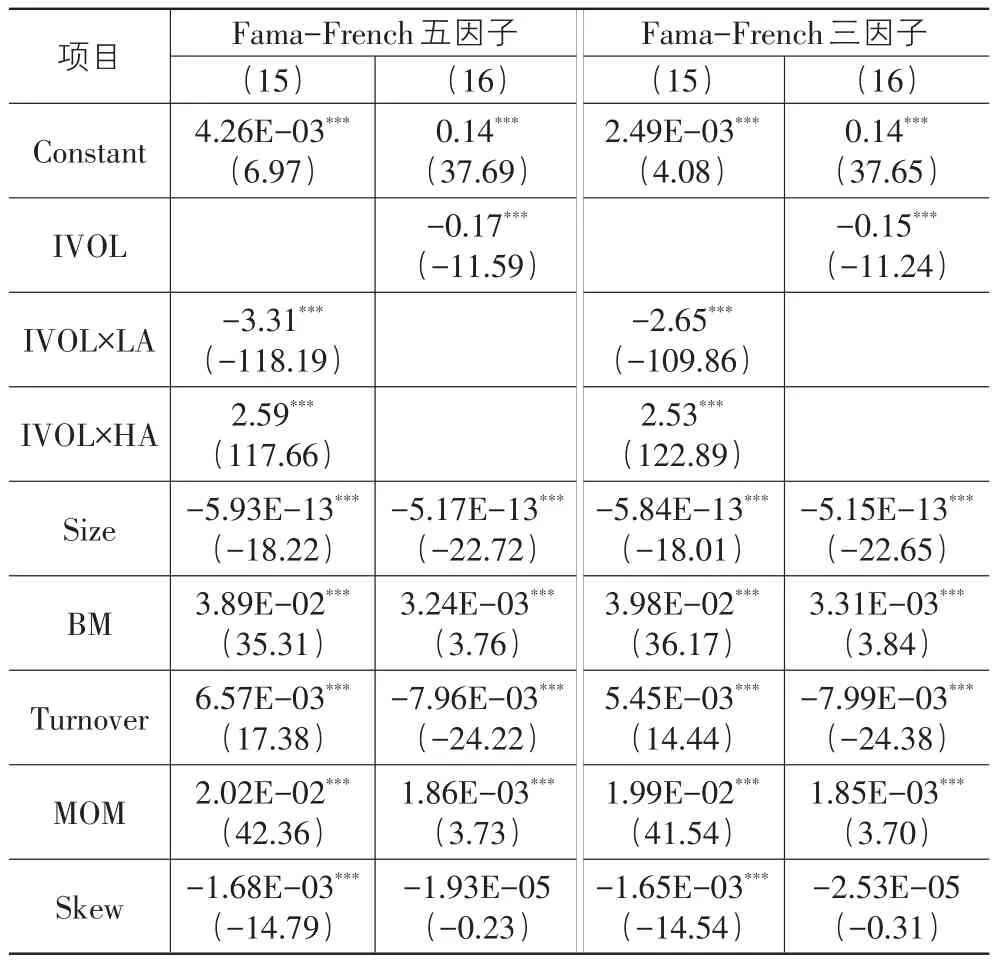
表7 面板模型的实证检验

表7的结果可以看出，无论使用原始数据进行面板回归，还是使用规模化处理数据进行分位数Fama-MacBeth回归，研究结论均未发生变化，我们的实证分析结论是稳健的。

六、结论与建议

（一）研究结论

本文建立了理论模型探究公司特质风险、估值水平与股票收益之间的关系，研究发现公司估值水平会对特质风险与股票收益率之间的关系产生影响：对于被高估的公司，特质风险主要来源于投资者的非理性交易行为，其噪声交易效应更为明显，因此特质风险与预期收益率呈负相关关系；对于被低估的公司，特质风险主要来源于公司的特质信息，其私有信息效应更为明显，因此特质风险与预期收益率呈正相关关系。在此基础上，我们从公司估值水平和卖空限制的角度对整体市场的特质波动率之谜进行了理论解释。我们使用2000年1月4日到2015年12月31日中国沪深两市的全部上市公司的数据进行了实证研究，基于分组检验和分位数Fama-MacBeth回归方法的实证分析结果支持了理论模型的结论：中国股票市场存在明显的特质波动率之谜，公司的估值水平不同，其预期收益率与特质波动率之间的关系也不同。最后，我们从变量替换、样本划分及计量方法三个层面验证了结论的稳健性。

（二）研究建议

文章提出的基于公司估值水平与卖空限制角度的理论解释，不仅丰富了特质波动率领域相关研究的理论体系，而且为上市公司的风险管理和投资者的交易决策提供了有价值的参考。根据本文的研究结论，提出以下政策建议：第一，虽然整体市场上特质波动率之谜显著存在，但公司的估值水平会影响特质风险与预期收益之间的关系，投资者在进行交易决策时应该关注公司的内在价值，不能盲目追逐低特质风险的股票。第二，公司特质风险体现私有信息的效率和卖空限制是造成特质波动率之谜的主要原因，为了维护资本市场的健康可持续发展，应该进一步加强监管力度，提高上市公司的信息透明度，同时不断完善我国股票市场的卖空机制，扩大融资融券标的，大力发展衍生品市场，通过套利交易的价格修正机制来增加股价的信息含量。

［1］Merton R C.A simple model of capital market equilibrium with incomplete information［J］.The Journal of Finance，1987，42（3）：483-510.

［2］Ang A，Hodrick R J，Xing Y，et al.The cross-section of vol⁃atility and expected returns［J］.The Journal of Finance，2006，61（1）：259-299.

［3］Ang A，Hodrick R J，Xing Y，et al.High idiosyncratic volatili⁃ty and low returns：International and further US evidence［J］.Journal of Financial Economics，2009，91（1）：1-23.

［4］Morck R，Yeung B，Yu W.The information content of stock markets：why do emerging markets have synchronous stock price movements？［J］.Journal of Financial Economics，2000，58（1）：215-260.

［5］Brandt M W，Brav A，Graham J R，et al.The idiosyncratic volatility puzzle：Time trend or speculative episodes？［J］.Review of Financial Studies，2010，23（2）：863-899.

［6］Fama E F，French K R.A five-factor asset pricing model［J］.Journal of Financial Economics，2015，116（1）：1-22.

［7］Campbell J Y，Lettau M，Malkiel B G，et al.Have individual stocks become more volatile？An empirical exploration of id⁃iosyncratic risk［J］.The Journal of Finance，2001，56（1）：1-43.

［8］Tinic S M，West R R.Risk，return，and equilibrium：A re⁃visit［J］.The Journal of Political Economy，1986，94（1）：126-147.

［9］Fu F.Idiosyncratic risk and the cross-section of expected stock returns［J］.Journal of Financial Economics，2009，91（1）：24-37.

［10］Huang W，Liu Q，Rhee S G，et al.Return Reversals，Idio⁃syncratic Risk，and Expected Returns.［J］.Review of Fi⁃nancial Studies，2010，23（1）：147-168.

［11］Jin L L.Idiosyncratic volatility，arbitrage risk，and anomaly returns［D］.Pennsylvania：University of Pennsylvania，2013.

［12］Xu Y，Malkiel B G.Investigating the behavior of idiosyn⁃cratic volatility［J］.The Journal of Business，2003，76（4）：613-645.

［13］Jiang G J，Xu D，Yao T.The information content of idio⁃syncratic volatility［J］.Journal of Financial and Quantita⁃tive Analysis，2009，44（1）：1-28.

［14］Guo H，Savickas R.Relation between time-series and cross-sectional effects of idiosyncratic variance on stock re⁃turns［J］.Journal of Banking&Finance，2010，34（7）：1637-1649.

［15］Fink J D，Fink K E，He H.Expected idiosyncratic volatili⁃ty measures and expected returns［J］.Financial Manage⁃ment，2012，41（3）：519-553.

［16］Guo H，Kassa H，Ferguson M F.On the relation between EGARCH idiosyncratic volatility and expected stock returns［J］.Journal of Financial and Quantitative Analysis，2014，49（1）：271-296.

［17］Stambaugh R F，Yu J，Yuan Y.Arbitrage asymmetry and the idiosyncratic volatility puzzle［J］.Journal of Finance，2015，70（5）：1903-1948.

［18］Rachwalski M，Wen Q.Idiosyncratic risk innovations and the idiosyncratic risk-return relation［J］.Review of Asset Pricing Studies，2016，6（2）：303-328.

［19］Barberis N，Huang M.Stocks as lotteries：The implications of probability weighting for security prices［J］.The Ameri⁃can Economic Review，2008，98（5）：2066-2100.

［20］Boyer B，Mitton T，Vorkink K.Expected idiosyncratic skew⁃ness［J］.Review of Financial Studies，2010，23（1）：169-202.

［21］Bali T G，Cakici N，Whitelaw R F.Maxing out：Stocks as lotteries and the cross-section of expected returns［J］.Journal of Financial Economics，2011，99（2）：427-446.

［22］Han B，Kumar A.Speculative retail trading and asset pric⁃es［J］.Journal of Financial and Quantitative Analysis，2013，48（2）：377-404.

［23］Han Y，Lesmond D.Liquidity biases and the pricing of cross-sectional idiosyncratic volatility［J］.Review of Finan⁃cial Studies，2011，24（5）：1590-1629.

［24］Boehme R D，Danielsen B R，Kumar P，et al.Idiosyncratic risk and the cross-section of stock returns：Merton（1987）meets Miller（1977）［J］.Journal of Financial Markets，2009，12（3）：438-468.

［25］Duan Y，Hu G，McLean R D.Costly arbitrage and idiosyn⁃cratic risk：evidence from short sellers［J］.Journal of Finan⁃cial Intermediation，2010，19（4）：564-579.

［26］Johnson T C.Forecast dispersion and the cross section of expected returns［J］.The Journal of Finance，2004，59（5）：1957-1978.

［27］Chen Z，Petkova R.Does idiosyncratic volatility proxy for risk exposure？［J］.Review of Financial Studies，2012，25（9）：2745-2787.

［28］邓雪春，郑振龙.中国股市存在“特质波动率之谜”吗？［J］.商业经济与管理，2011（1）：60-67.

［29］罗登跃.特质波动率与横截面收益：基于Fama—French股票组合的检验［J］.统计与决策，2013（4）：167-169.

［30］熊伟，陈浪南.股票特质波动率、股票收益与投资者情绪［J］.管理科学，2015（5）：106-115.

［31］徐小君.公司特质风险与股票收益——中国股市投机行为研究［J］.经济管理，2010（12）：127-136.

［32］杨华蔚，韩立岩.外部风险、异质信念与特质波动率风险溢价［J］.管理科学学报，2011（11）：71-80.

［33］左浩苗，郑鸣，张翼.股票特质波动率与横截面收益：对中国股市“特质波动率之谜”的解释［J］.世界经济，2011（5）：117-135.

［34］黄卓，康辰，王小华.中国股市“特质性波动率之谜”研究［J］.山东社会科学，2015（7）：161-166.

［35］张宇飞，马明.中国证券市场预期特质性波动率影响定价的实证研究［J］.当代财经，2013（4）：59-72.

［36］李竹薇，史永东，于淼，等.中国股票市场特质波动率异象及成因［J］.系统工程，2014（6）：1-7

［37］赵胜民，闫红蕾，张凯.Fama-French五因子模型比三因子模型更胜一筹吗——来自中国A股市场的经验证据［J］.南开经济研究，2016（2）：41-59.

［38］Mashruwala C，Rajgopal S，Shevlin T.Why is the accrual anomaly not arbitraged away？The role of idiosyncratic risk and transaction costs［J］.Journal of Accounting and Economics，2006，42（1）：3-33.

Abstract:This paper builds a theoretical model to explore the relationship among idiosyncratic volatility,valuation level and stock re⁃turns,the conclusions of the theoretical model indicate:The IVOL-return relation is positive among underpriced stocks because idiosyn⁃cratic volatility mainly represents firm’s idiosyncratic information;Whereas the IVOL-return relation is negative among overpriced stocks because idiosyncratic volatility mainly represents the behavior of noise traders.Then we present a theoretical interpretation of the whole market’s IVOL puzzle from the perspective of valuation level and short sale constraints.We use Fama-French five-factor model to esti⁃mate the idiosyncratic volatility and the valuation level,apply portfolio sorting method and quantile Fama-MacBeth regression model for the empirical test.The empirical analysis results based on China listed companies support the conclusions of the theoretical model:The IVOL puzzle of Chinese stock market is robust,and the valuation level of a company will influence the relationship between idiosyncratic volatility and stock returns.

Keywords:idiosyncratic volatility;valuation level;private information;noise trading

［责任编辑：张 青］

Idiosyncratic Volatility,Valuation Level and Stock Returns—An Empirical Analysis Based on Quantile Fama-MacBeth Regression Model

ZHAO Sheng-min,LIU Xiao-tian

(School of Finance,Nankai University,Tianjin 300350,China)

F276.6；F830.91

A

1007-5097（2017）09-0035-10

10.3969/j.issn.1007-5097.2017.09.005

2017-05-06

教育部社会科学基金项目（15YJA790090）

赵胜民（1967-），男，黑龙江齐齐哈尔人，教授，博士生导师，研究方向：衍生产品定价，资本市场稳定性；刘笑天（1991-），男，辽宁沈阳人，博士研究生，研究方向：资产定价，量化投资。