改进小波阈值法在木材图像缺陷处理中的应用

王 旭，李小舟，雷庆锋，李艳杰

（辽宁林业职业技术学院，辽宁沈阳 110101）

改进小波阈值法在木材图像缺陷处理中的应用

王 旭，李小舟，雷庆锋，李艳杰

（辽宁林业职业技术学院，辽宁沈阳 110101）

阈值的选取和小波函数的构造是小波阈值去噪的关键，但传统的阈值去噪方法并没有对此进行充分的研究。针对传统小波阈值去噪分析的不足，分别从2个方面进行改进。首先，根据小波系数在各尺度上的相关性，提出了基于Lip指数阈值寻优的新方法；其次，用构造出新的小波阈值函数处理小波系数，克服了软阈值的高阶不可导和硬阈值函数的不连续，且计算方便。最后，对带有节子裂缝的木材图像进行去噪处理。实例验证了改进小波阈值法的优越性和有效性。

木材缺陷；小波去噪；阈值函数；图像处理；均方误差

Abstract：Threshold selection and wavelet function construction were two key points of wavelet threshold denoising,which were not researched adequately in traditional threshold denoising methods.Deficiencies of traditional wavelet threshold methods in denoising were improved in two aspects.Firstly,according to the correlations of wavelet coefficients in different scales,new method for searching optimal threshold were proposed based on Lip exponent;secondly,new wavelet function was constructed to deal with wavelet coefficients,which not only convenient in calculating but also could overcome the non-differentiability in higher order of soft threshold and discontinuity of hard thresholding function;lastly,denoising treatment was done to the images of wood with knots and cracks.The superiority and effectiveness of improved wavelet thresholding method were tested.

KeyWords：wood defects;wavelet denoising;threshold function;picture processing;mean squared error

引言

节子是树木在生长过程中最普遍存在的一种现象。它不仅破坏木材纹理构造的完整性和均匀性[1-2]，使纹理质量下降，大大降低木材的档次，而且会给木材加工工艺带来一些困难，降低木材的利用效率。由于木材的裂缝节子的像素值和木材背景颜色相近，边缘也不清晰，会造成木材纹理混淆、分析困难等问题，因此必须要对带有节子裂缝的木材图像进行去噪处理，将节子裂缝部分最大平滑的同时保护纹理的细节部分[3]，改善木材强度性质，提高木材加工工艺的利用率。

小波阈值去噪法因其具有多分辨率分析的特点，已被广泛应用于木材图像去噪处理中[4-5]，但是传统的小波阈值去噪能力有限，所以很多学者提出了相应的改进方法。在阈值的选取上改进的方法有BayesShrink阈值、Mapshrink阈值等，对于阈值函数的改进方法有软硬阈值折中法、半软阈值法和模平方处理法[6]。这些方法虽然取得了一定的成果，但是去噪的效果还需要进一步改进。因此，在小波阈值去噪中应用了一些新的方法，如袁凯明等将模拟退火算法应用于最优阈值的求解[7]，臧玉萍等提出了一种分层阈值的小波阈值去噪处理方法[8]，焦明连等将灰色预测模型和小波分析结合起来[9]。这些新的方法都取得了不错的去噪效果。本文对阈值函数进行了改进，而对阈值选取，将小波系数与分解层数的相关Lip指数应用到最优阈值的求解中，提出新的阈值选取的方法，并通过实例证明该方法的优越性和有效性。

1 小波阈值法去噪

1.1 小波阈值去噪的基本思想

1995 年，D.L.Dohono在小波变换的基础上提出了阈值去噪的方法，其基本思想是[10-11]：带有噪声的信号在经小波分解后，得到代表噪声的高频系数以及代表有用信号的低频系数。于是可以找到一个合适的阈值，对小波分解后的系数进行阈值量化处理，即绝对值小于给定阈值的系数置为零，而让绝对值大于给定阈值的系数保留或者收缩，得到估计的小波系数，然后再用这些估计的小波系数重构信号，即达到去噪的目的。

1.2 小波阈值去噪算法的步骤

①小波变换：选定1种小波基函数，确定小波分解层数，对信号进行小波分析；

②阈值的确定：确定阈值选取的准则；

③阈值量化处理：选择合适的阈值函数对小波系数进行阈值量化处理；

④小波重构：将处理后的系数通过小波重建恢复原始信号。

2 改进小波阈值去噪方法

从上述小波阈值去噪算法的步骤来看，阈值的选取和阈值函数选择是小波阈值去噪的关键。传统的小波阈值去噪方法在这2个方面还存一些不足[12]：①小波进行变换时如果每层选择相同的阈值对小波系数阈值量化处理，这样可能会将一些有信号的高频系数剔除掉，同时还会保留一些含有噪声的低频信号，会造成重构后的信号失真；②在进行阈值处理时，所选用的软、硬阈值方法虽然已经在实际工程中得到广泛的应用，但其本身还有一些缺陷：如图1所示，在进行硬阈值函数处理过程中，由于估计的小波系数不是连续的，会造成重构后的信号就会产生一些震荡；而软阈值函数虽然解决了硬阈值函数不连续的问题，但由于对所有大于阈值的系数做了收缩，使处理后的小波系数与原小波系数之间存在恒定的偏差。本文针对这两方面的不足，采用的改进方法如下。

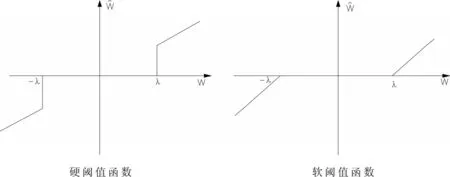
图1 软、硬阈值函数示意图

2.1 各层采用不同阈值[13]

其中：WT2jx(t)是第j层小波分解系数α为Lip指数；K为一个常数。Lip指数与信号的平滑度有关，α越大，信号越平滑。对于一般的信号，有用信号的Lip指数为正，即有用信号的小波系数随分解尺度j增大而变大。而带有白噪声的信号Lip指数为负，即白噪声信号的小波系数随分解尺度j增大而变小。

白噪声的Lip指数满足：

由式（1）和式（2）可知

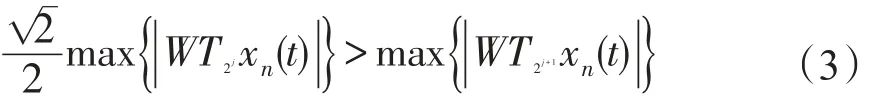
其中：WT2jxn(t)为白噪声对应的第j层小波系数。

由式（3）可以看出第j+1层对应的白噪声小波系数的最大值小于第j层对应的白噪声小波系数的最大值的倍，因此，本文先采用通用阈值λ1（sqtwolog规则）确定第一层阈值，以后各层阈值为前一层阈值的倍，即λj+1=

2.2 改进的阈值函数

针对软、硬阈值在去噪方面的不足，本文对阈值函数进行了改进，阈值函数如下：

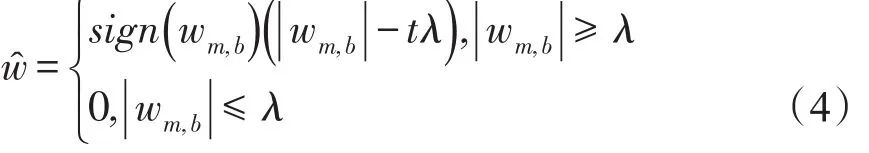
式中：参数α、β均为大于1的常数，并且根据实际情况可以调整。而

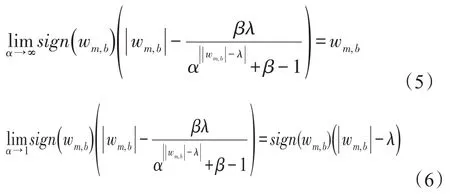
从式（5）和式（6）可以看出来，当α→∞时式（4）接近硬阈值函数；而当α→1时式（4）接近软阈值函数，并且新的阈值函数还可以通过调整α和β的值来得到不同的去噪效果。考虑函数

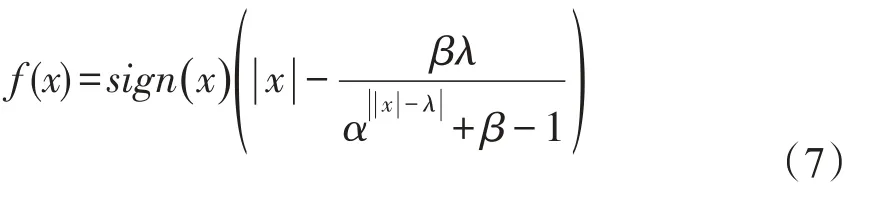
当x＜0时,

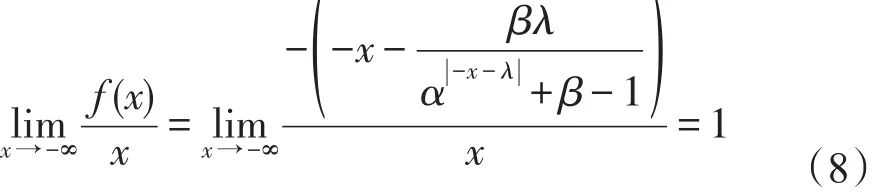
当x＞0时，

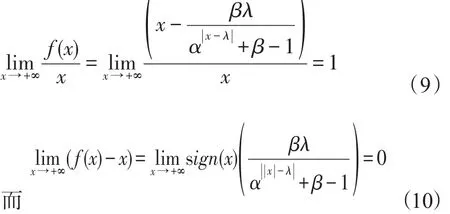
3 算例分析和比较

本文选用的研究对象为雪松图像，将雪松制成尺寸为100 mm×80 mm木材径向切面，图像采样精度选为1 024×1 024像素，保存为.JPG图像格式。采集到的木材灰度图像如图2所示，利用小波阈值去噪法对带有噪声的木材图像进行去噪处理。

3.1 小波阈值去噪性能的评价标准

本文以信噪比SNR和均方根误差RMSE为标准，评定本文改进的阈值函数的去噪效果。信号去噪后信噪比越大、均方误差越小，去噪的效果越好[14-15]。

3.2 各种阈值选取准则去噪效果分析

本文采用MATLAB软件，以含有噪声的木材图像作为原始，采用通用阈值准则及本文提出的分层阈值选取准则，小波函数为sym4，采用传统的硬阈值函数，分解层数取3，去噪效果如图2所示。

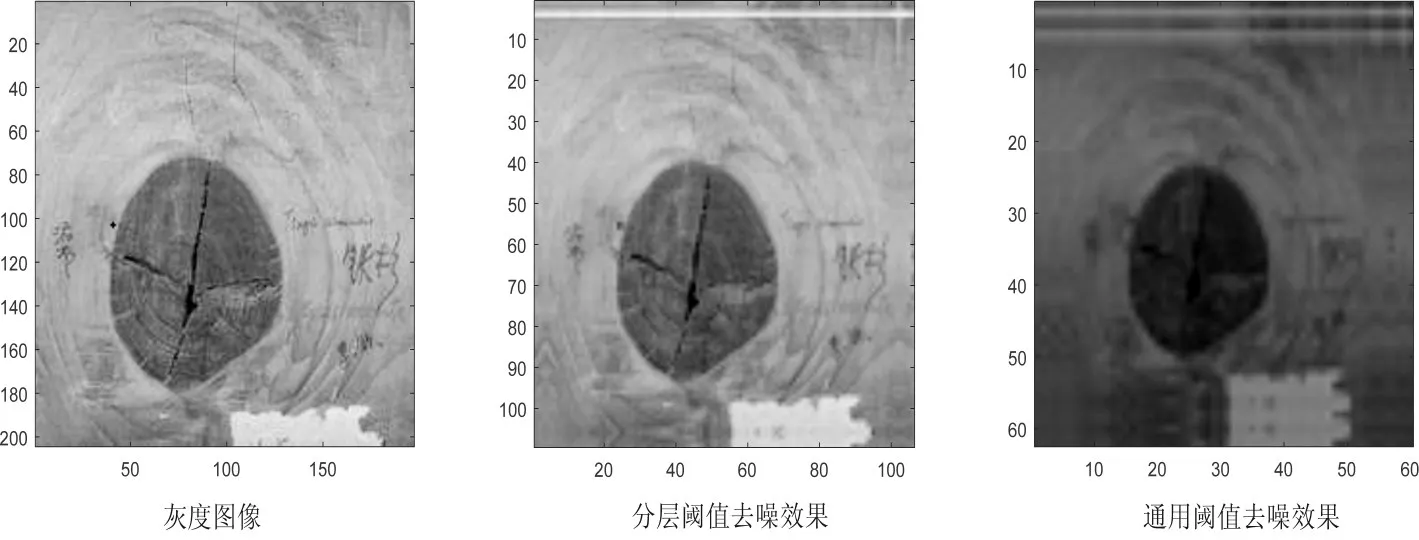
图2 两种阈值去噪比较

从图2可以看到，由于通用阈值对于小波系数有严重的“过扼杀”倾向，尤其是将较高频率的有信号当做噪声去除掉，导致去噪后的图像失去原有的纹理，图像失真。而分层阈值去噪的方法去噪后，节子周围的小裂痕消失，大裂痕变小，本文的方法很好地保留了图像纹理的同时消除了更多的噪声系数，使去噪后的图像更加接近真实值。通过表1也能看出分层阈值去噪方法在信噪比（SNR）和均方差（MSE）都优于通用阈值去噪法，充分说明了分层阈值法的实效性和优越性。

表1 两种方法降噪性能比较

3.3 各种阈值函数去噪效果分析

选取sym4小波函数，分解层数为3层，阈值选取准则为分层阈值准则，阈值函数采用传统的硬阈值函数、文献[6]和本文改进的阈值函数进行去噪处理，文献[6]中α取0.3，式（4）α和β分别取α=2 000、β=13，去噪效果如图3所示。

图3 4种阈值去噪比较

从图3明显看出，硬阈值函数在处理过程中节子周围没有变化，图像周围平滑了，同时有些模糊。文献[6]和本文改进方法去噪后，节子周围的小裂痕消失，大裂痕变小，去噪点也变少了，达到了比较好的去噪效果。从表2也可以看出，文献[6]改进的方法和本文改进方法去噪后的信噪比和均方差都优于传统的硬阈值函数，并且本文改进方法去噪后的信噪比最高，均方差最小，并且在一定范围内选取适当的α和β值，去噪效果会更明显。

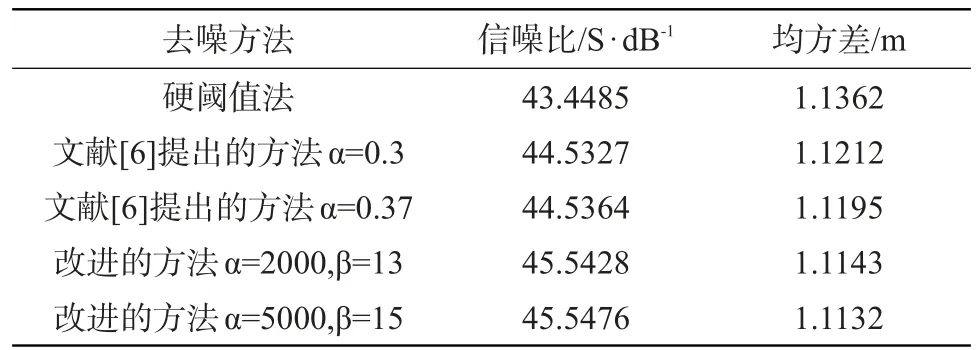
表2 3种阈值去噪方法比较

4 结 论

4.1 将改进小波阈值去噪方法应用到木材缺陷图像的边缘检测中，实现木材缺陷的有效识别与提取。

4.2 本文对小波阈值去噪法做了两方面的改进——Lip指数阈值寻优法和提出改进阈值函数，比传统的阈值选取规则去噪及软、硬阈值去噪方法在信噪比和均方差上都有所提高。本文改进的新阈值函数有两个待定系数α和β，它们会直接影响到去噪的效果，如果选择得当会更能体现出新方法的优越性。

4.3 小波函数、分解层数、阈值选择准则和阈值函数的选取都会直接影响到小波去噪的效果，如何选取最优小波函数及分解层数还要进一步的研究。

［1］于海鹏.基于数字图处理学的木材纹理定量化研究[D].哈尔滨：东北林业大学，2005：4.

［2］于海鹏，刘一星.基于小波的木材纹理分频信息提取与分析[J].林业科学，2005，3（41）：100-105.

［3］褚标.小波理论在图像去噪与纹理分析中的应用研究[D].合肥：合肥工业大学，2008：4.

［4］杨熙.小波分析在木材缺陷图像处理中的应用[D].哈尔滨：东北林业大学，2011：4.

［5］王亚超.基于小波变换的木材图像处理技术研究[D].呼和浩特：内蒙古农业大学，2013：6.

［6］朱建军，章浙涛，匡翠林，等.一种可靠的小波去噪质量评价指标[J].武汉大学学报：信息科学版，2015，40(9):688-693.

［7］袁开明，舒乃秋，孙云莲，等.基于阈值寻优法的小波阈值去噪分析[J].武汉大学学报：信息科学版，2015，48（1）:74-79.

［8］纪跃波.小波包的频率顺序[J].振动与冲击，2005，24（3）:96-98.

［9］焦明连，蒋廷臣.基于小波分析的灰色预测模型在大坝安全监测中的应用[J].大地测量与地球动力学，2009，29（2）:115-117.

［10］DONOHO D L，JOHNSTONE M.

Ideal Spatial adaptation by wavelet shrinkage[J].Biometrika，1994，81(3):425-455.

［11］ DONOHO D L，JOHNSTONE I M.Adapting to unknown smoothness via wavelet shrinkage[J].Journal of TheAmerican stat assoc，1995，12(90):1200-1224.

［12］张维强，宋国乡.基于一种新的阈值函数的小波域信号去噪[J].西安电子科技大学学报，2004，31（2）：296-303.

［13］Xu K,Wang X,Li Y，et al.Fundamental wave extraction and frequency measurement based on IIR wavelet filter banks[J].measurement,2007,40(6):665-671.

［14］邵鸿翔，高宏峰．改进小波阈值去噪方法处理FBG传感信号[J].激光与红外，2014，44(1):73-76．

［15］陶珂，建军.多指标融合的小波去噪最佳分解尺度选择方法[J].测绘学报，2012，41（5）:749-755.

(责任编辑：董莉莉)

Application of improved wavelet thresholding method in defect processing of timber image

WANG Xu,LI Xiaozhou,LEI Qingfeng,LI Yanjie
（LiaoningForestryVocationTechnicalCollege,Shenyang110101,China）

S781.5

A

1001-1714（2017）05-0018-05

2017-05-25

小波阈值去噪法在变形监测数据处理中的应用研究（KJ201505）。

王旭（1983-），男，讲师，主要从事变形监测数据处理。E-mail：wangxu19830411@126.com。