公路山岭隧道初期支护极限相对位移的确定

徐东强， 燕 鹏， 李彦奇， 王可意

(河北工业大学土木与交通学院， 天津 300401)

公路山岭隧道初期支护极限相对位移的确定

徐东强， 燕 鹏*， 李彦奇， 王可意

(河北工业大学土木与交通学院， 天津 300401)

为计算公路山岭隧道初期支护的极限相对位移值，采用霍克布朗屈服准则，依据公路隧道设计规范和实际工程经验选取断面形式、支护方式以及材料参数，采用短台阶的开挖方式，对各级围岩不同埋深下3车道公路山岭隧道拱顶、拱腰和拱脚的极限相对位移值采用FLAC3D进行三维数值模拟，并依据突变理论确定。根据对计算结果的统计分析，提出可将洞周变形控制点位明确，细化埋深范围，通过分析上下开台阶开挖对不同点位变形值的影响，且与实际施工相结合，确定出开挖步的变化对洞周位移的影响。

公路隧道； 突变理论； 围岩稳定； 极限相对位移； 初期支护； FLAC3D模拟分析

Abstract: In order to calculate the ultimate relative displacement of primary support of mountain-crossing highway tunnel, the Hoek-Brown criterion is adopted; the highway tunnel standards, cross-section pattern, supporting methods and material properties are taken as references; short bench excavation method is adopted; and the ultimate relative displacements of crown top, arch springer and arch feet of the three-lane highway tunnel under different grades of surrounding rocks and buried depths are simulated and calculated by software FLAC3Dand are further determined by catastrophe theory. According to the statistical analysis of calculation results, it is pointed out that the deformation control points of the tunnel surrounding can be defined clearly and the buried depth can be refined; by analyzing the influences of benches excavation on deformation of different points and comparing to field construction, the influence of the excavation step on the displacement of tunnel surrounding can be determined.

Keywords: highway tunnel; catastrophe theory; stability of surrounding rock; ultimate relative displacement; primary support; FLAC3Dsimulation analysis

0 引言

随着岩石力学理论的发展和完善，新奥法原理已经成为隧道及地下工程施工中普遍遵循的原理。新奥法与传统的隧道设计施工理念有着本质的区别，其核心是保护围岩，合理利用围岩的自身承载能力，使围岩从向隧道结构施加荷载的加载体变为隧道支护系统的主要承载单元。由于围岩的弹、塑性力学特征，允许围岩产生一定的变形，采用喷锚支护作为初期支护结构，使其与围岩紧密接触，共同作用以达到洞室围岩稳定的目的。基于围岩和人工支护系统之间的相互作用关系，开挖面附近支护位移值的大小可以作为直接判断隧道围岩稳定性的重要依据。众多学者对衬砌的位移开展了广泛的研究： 张长亮等[1]通过对小净距2车道公路隧道极限位移值的研究，建立了围岩变形预警管理系统，并对其他预测预报方法进行了分类总结；崔宏伟等[2]利用不同的围岩应变释放率，采用突变原理，通过二维平面应变模型，模拟隧道开挖过程，确定出滑坡地段浅埋隧道围岩变形的极限位移值；朱永全等[3-4]针对铁路隧道单、双线断面的特点，提出以隧道初期支护的极限位移来判别隧道的稳定性，采用二维数值模拟的方法确定了各种极限相对位移的范围值,同时利用计算模拟确定大变形隧道的极限相对位移，建立稳定性判别准则。但目前对极限相对位移的研究大多数是针对2车道隧道采用二维平面应变理论，且使用的屈服准则并没有对岩体节理裂隙、非线性破坏等特征进行考虑。《公路隧道设计规范》[5]中给出了隧道洞室初期支护允许洞周相对收敛值的范围，如表1所示。但是对不同围岩级别，没有明确指出洞周不同位置的极限范围，也没有对埋深区段进行细化。因此，鉴于规范中的条款以及已有的研究成果，本文对3车道公路山岭隧道的极限相对位移值进行三维模拟研究，利用突变理论，采用霍克布朗屈服准则，归纳总结出洞室不同位置在不同的埋深下相对位移值的范围，以期为隧道施工提供有益的参考。

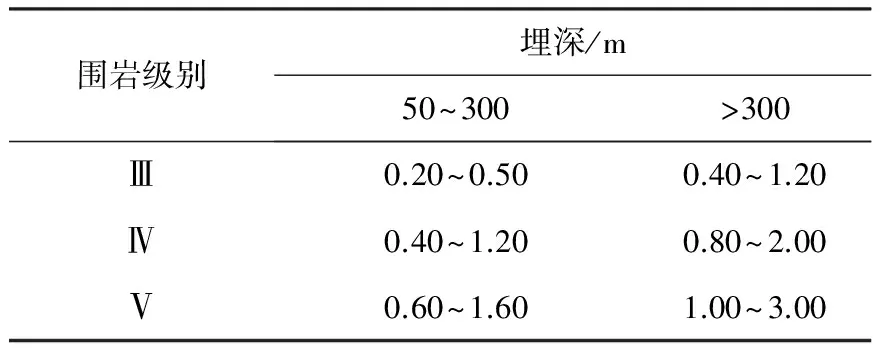
表1 隧道洞室允许洞周水平相对收敛值

1 极限位移的意义及确定方法

将位移作为隧道稳定性的判据，就是利用施工中监控量测的位移值与相应位置的极限位移值作对比。极限位移是指在施工各阶段，支护体系应发挥的某种功能的极限状态下各部位的位移[2]，隧道的位移值是隧洞开挖所引起的围岩变形最直观的表现。对于施工阶段而言，隧道洞室开挖至初期支护施作之前(即毛洞阶段)所处时间较短，给测量带来了很大不便；二次衬砌通常视为附加的安全储备，实测意义不大。因此用位移判别隧道稳定性，其核心就是初期支护阶段隧道极限位移值的确定。采用理论分析、现场监测统计、室内试验模拟并结合工程实际经验等手段来确定这一限值存在很多困难，室内试验模拟只能通过反复改变埋深、支护形式、围岩级别、隧道形状等条件，来获得不同状态下的极限位移，工作量大且经济性差；现场监测由于技术的限制，难以记录爆破瞬间洞室释放的弹性位移以及爆破后至施测前的位移丢失，同时很难统计极限破坏前极短时间下的位移值；而理论分析和工程经验又由于现有理论体系及人为因素的影响与实际条件有一定出入。鉴于此，综合各方面因素，利用数值模拟的方法可以更好地模拟符合围岩变形的实际情况，以支护结构与围岩相互作用的理论为依据来确定极限位移值，对于条件的改变和经济性都具有极大的优势。

2 初期支护极限位移的体现

隧道作为地下工程，属于高次超静定结构，围岩局部区域因受拉破坏而处于塑性状态，并不意味着将失去整体稳定性。只有当围岩极度松弛失稳，变形无法控制时，才会最终导致隧道发生坍塌。所以围岩的变形是造成围岩失稳破坏的充分条件[6]。

隧道洞室衬砌修筑后，会产生沿洞室周边的阻力pa，它通过阻止坑道围岩的变形，实现了对围岩二次应力状态的改变，支护阻力pa作为支护结构与隧道围岩相互作用的产物，其大小和方向对围岩应力状态有很大的影响。坑道应力的重分布，必然伴随着变形的发展，即坑道壁会产生向坑道内的径向位移u。但是考虑到客观实际，当围岩初始应力接近于支护阻力时，沿径向的洞壁位移将趋近于零，并且，不同围岩级别都有一个位移极限值，超过这个限值，围岩将会崩塌[7]。

支护体系开始出现塑性变形时的位移为ui，但塑性变形的出现并不意味着初期支护一定失稳破坏，随着变形的加剧，开裂与破坏的截面数量不断增加，当发展到一定程度时，因围岩失稳发生完全塑性破坏而导致支护体系失去其作用，表现为位移曲线的趋势发生突变，此时对应的位移为ui，max，所以最终的初期支护极限位移为ui～ui，max。

为了进一步理解围岩与支护的相互作用以及支护形式对围岩变形的影响，根据不同支护结构的特性可得支护特性曲线与围岩特性曲线的关系，如图1所示。从洞室开挖到支护起作用之前，隧道洞室会发生一定的弹性位移u0。图1中，特征曲线1表示初期支护只采用喷射混凝土，它与代表整体性较好的Ⅰ、Ⅱ级围岩的特征曲线A相交，只发生弹性位移或少量塑性位移，其极限位移为ua～ua，max;特征曲线2表示锚喷支护，其与代表塑性变形明显的围岩特性曲线B的交点为b，相应的极限值为ub～ub，max；特性曲线3表示锚杆、钢拱架、钢筋网和喷射混凝土共同作用，在合适的支护时间下设置，其与围岩特性曲线B的交点为c，而且由于这种支护形式具有较大的支护刚度，可以提供更大的支护阻力，因而可承受较大的变形，所以极限位移值为uc～uc，max。可见，初期支护极限位移值范围的确定就是围岩和支护之间相互关系的体现。

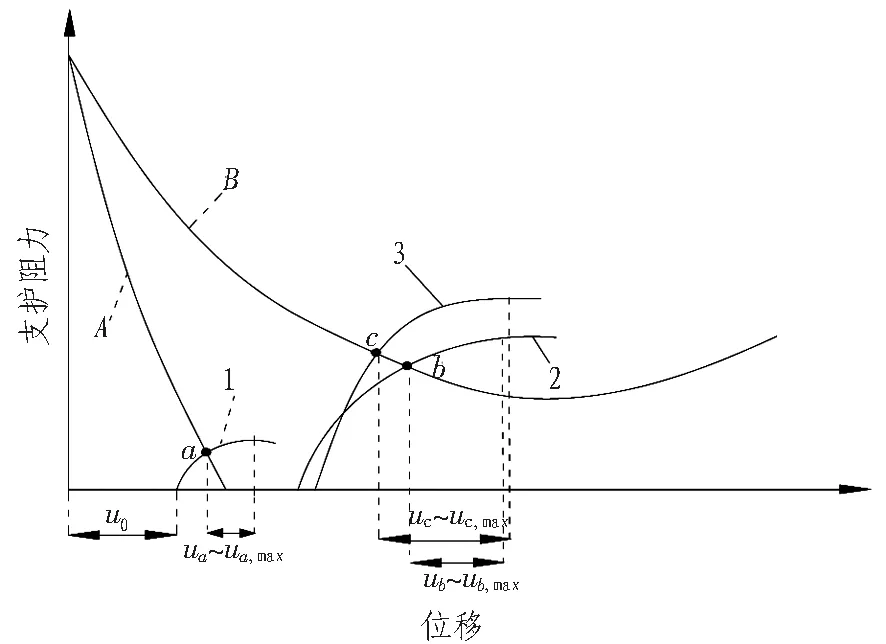
图1 支护特性曲线与围岩特性曲线关系图

Fig. 1 Relationship between support and surrounding rock reaction curves

3 极限相对位移的模拟分析

综合规范以及支护与围岩的特性关系，为了使数值模拟的结果更加符合工程实际，考虑多方面因素对极限相对位移值的影响，本文选取实际工程中常见的3车道公路山岭隧道，采用FLAC3D对初期支护过程中拱顶相对沉降值、拱腰和拱脚的水平相对收敛位移值进行模拟研究。

3.1计算模型及参数选取

模型的断面形式根据《公路隧道设计规范》和实际工程经验，Ⅲ级围岩为三心圆仰拱隧道，Ⅳ、Ⅴ级围岩采用五心圆仰拱隧道。开挖方法采用上下台阶法，建立长度为24 m的三维模型，左、右边界按开挖宽度5倍取值，距中心点左右各为78 m；下部边界按开挖高度4倍取值，距中心点以下40 m。开挖进尺为3 m，上台阶超前下台阶12 m,选取Y=12 m处作为监控断面，每一个开挖步完成后立刻施作锚杆，喷射混凝土等相应支护措施。第1—4步完成上台阶12 m长的开挖支护，并第1次提取测点的监控值；第5—12步交替完成上、下台阶的开挖支护，当下台阶开挖支护至Y=12 m时，做第2次数值监控；第13—16步完成全部隧道的开挖支护模拟，且当初衬位移达到极限条件时，得到第3次采样测点的位移值。具体开挖及测点布置如图2所示。

图2 开挖及测点布置示意图

Fig. 2 Layout of excavation steps and monitoring points

初期支护考虑锚杆、钢拱架、钢筋网和喷射混凝土的共同作用。依据相应规范和我国公路隧道的设计施工经验，具体参数如下：

1)锚杆采用中空注浆锚杆，直径为22 mm，Ⅲ级围岩时长度为3.5 m，纵向间距为1 m； Ⅳ—Ⅴ级围岩时长度为4 m，纵向间距为0.8 m。

2) Ⅳ—Ⅴ级围岩钢拱架采用工字钢，型号为Ⅰ18，沿隧道纵向间距为1 m，Ⅲ级围岩无钢拱架。

3)初期支护喷射混凝土为C25，Ⅲ级围岩时喷射厚度为15 cm，Ⅳ—Ⅴ级围岩时喷射厚度为20 cm。

锚杆采用Cable单元模拟，喷射混凝土采用Shell单元模拟，用Null模型来模拟隧道开挖部分。上下台阶施工法计算模型如图3所示，支护模型如图4所示。在FLAC3D数值模拟中，钢拱架一般不单独划分单元，其作用可通过提高结构强度指标近似模拟，或者采用等效的方法考虑钢拱架及钢筋网，即将钢拱架或钢筋网的弹性模量折算给喷射混凝土的弹性模量，其计算方法公式为：

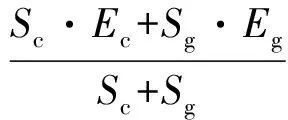
(1)

式中：Ec′为折算后的混凝土弹性模量；Ec为原混凝土的弹性模量；Sg为钢拱架或钢筋网截面面积；Sc为混凝土截面面积；Eg为钢材弹性模量。

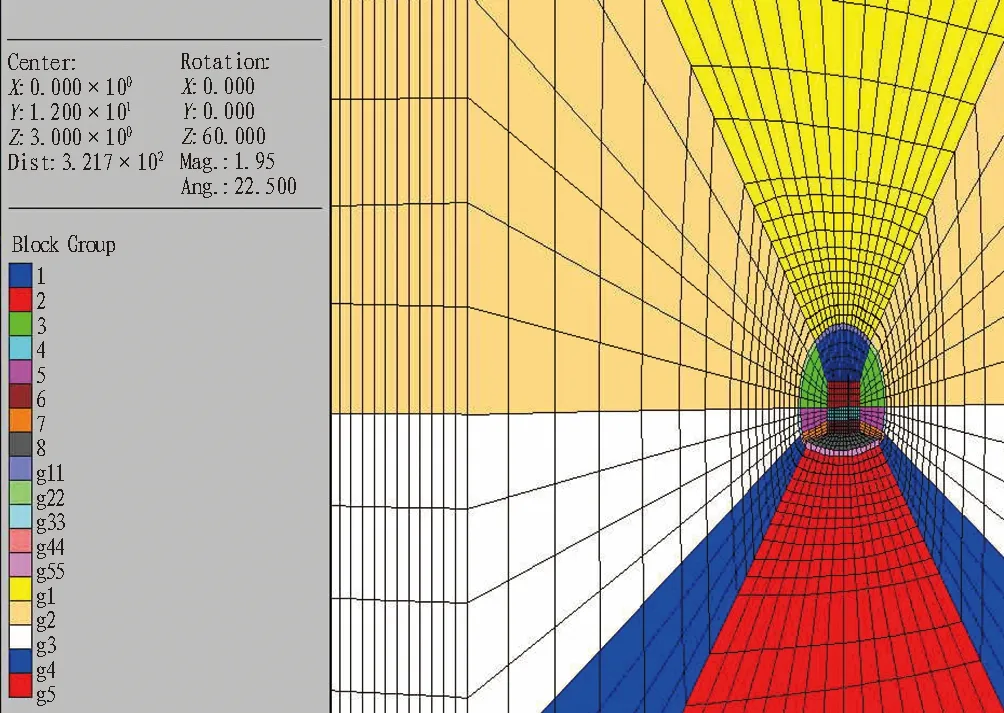
图3 计算模型Fig. 3 Calculation model

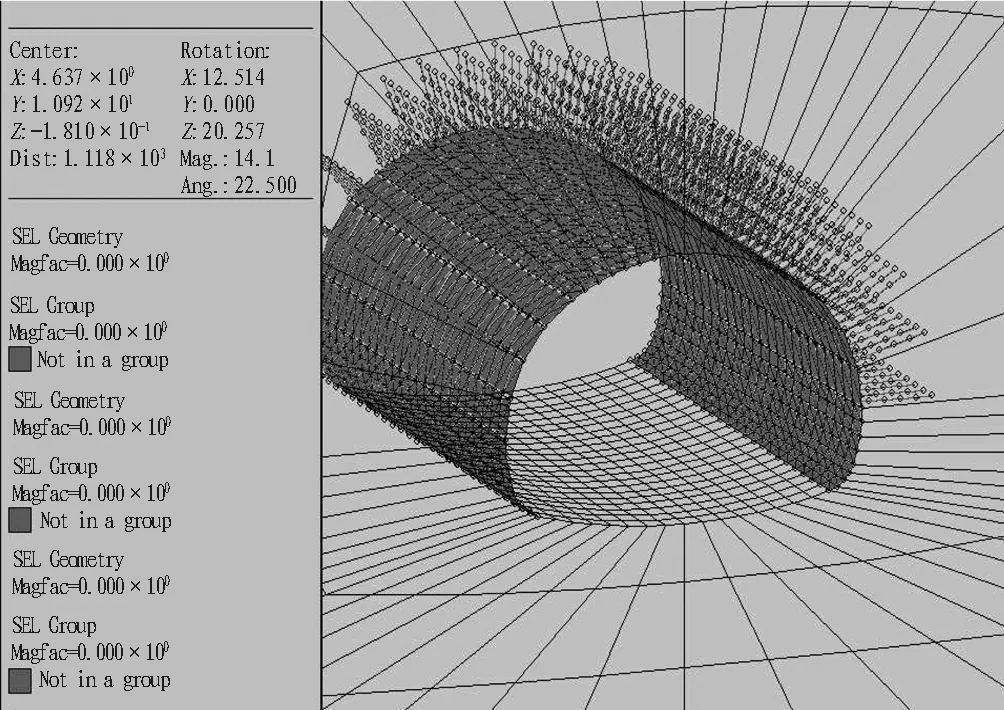
图4 支护模型Fig. 4 Support model

根据《公路隧道设计规范》以及《公路隧道设计细则》[8]，最终的初期支护力学参数如表2所示。

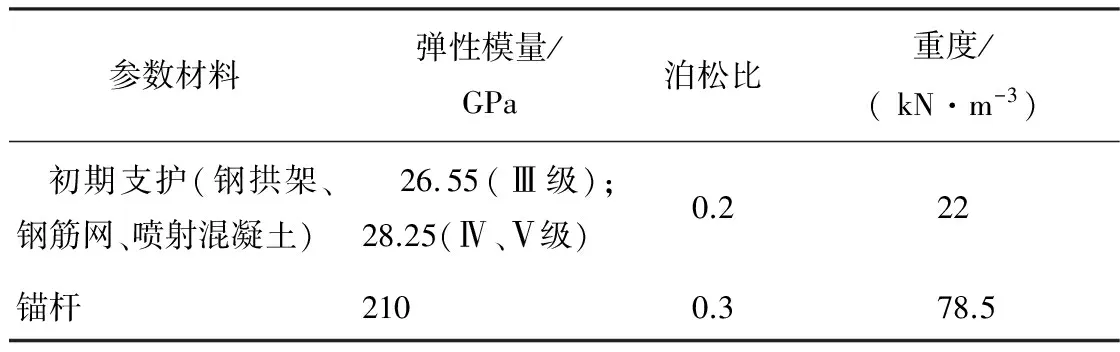
表2 初期支护力学参数表Table 2 Mechanical parameters of primary support

在极限相对位移值的计算模拟中，初始地应力仅考虑自重应力场。根据隧道开挖理论与实际经验，模型四周设为法向位移约束，底部边界为全部约束，上边界为自由边界。针对围岩节理裂隙以及非线性破坏等特征，采用霍克布朗屈服准则，综合考虑岩体结构、岩块强度、应力状态等因素，其参数mb、s基于地质强度指标GSI由式(2)和式(3)确定[9-12]，量化的GSI围岩分级系统和霍克布朗岩体破坏准则，综合各种地质信息，可实用、高效地估算岩体的力学参数。因此围岩各项物理力学指标及参数如表3和表4所示。

1)当GSI>25.0(Ⅲ级围岩)时，

(2)

2)当 GSI<25.0(Ⅳ—Ⅴ级围岩)时，

(3)

表3 Ⅲ—Ⅴ级围岩物理力学参数表

Table 3 Physico-mechanical parameters of Grade Ⅲ to Grade Ⅴsurrounding rocks

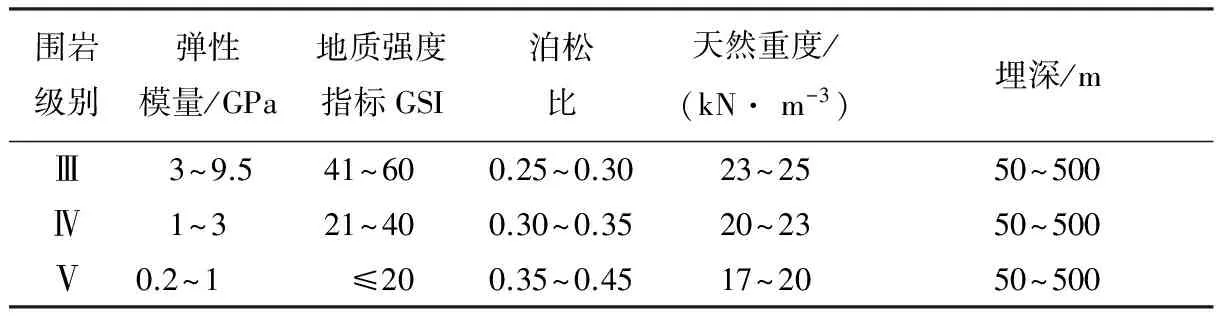
围岩级别弹性模量/GPa地质强度指标GSI泊松比天然重度/(kN·m-3)埋深/mⅢ 3～9．541～600．25～0．3023～2550～500Ⅳ 1～321～400．30～0．3520～2350～500Ⅴ0．2～1≤200．35～0．4517～2050～500

表4地质强度指标GSI与岩体参数mb、s对照表

Table 4 Geological strength index GSI and rock mass parametersmbands

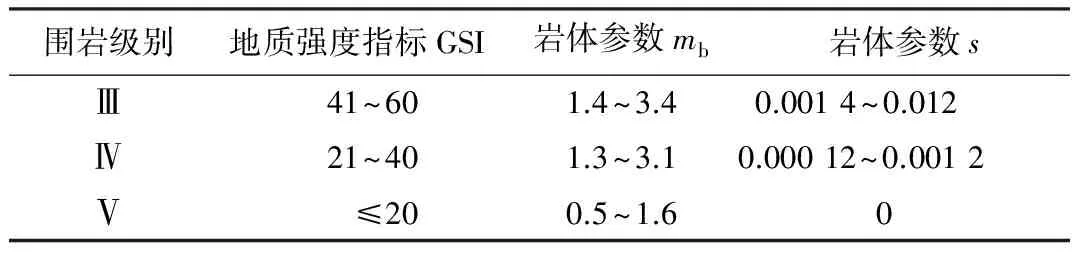
围岩级别地质强度指标GSI岩体参数mb岩体参数sⅢ41～601．4～3．40．0014～0．012Ⅳ21～401．3～3．10．00012～0．0012Ⅴ≤200．5～1．6 0

3.2数值模拟结果分析

在公路隧道极限位移的计算模拟中，采用参数分位值抽样的计算方法，即对弹性模量、地质强度指标、天然重度、泊松比分别选取最小值、最大值、1/4分位值、1/2分位值和3/4分位值5个不同分位值在埋深为50、100、150、200、300、400、500 m这7种情况下进行交叉取值计算。该方法考虑各范围值的全面综合影响，体现了参数随机变异性的特点。

隧道开挖引起的围岩失稳破坏可以看作是一个突变过程，因此可用突变理论判断围岩的稳定性，突变模型的标准形式如式(4)所示，根据突变理论得出的特征值如式(5)所示。

u=a4x4+a3x3+a2x2+a1x+C。

(4)

式中：u为测点的位移值；x为开挖计算步数；C为一个对突变无意义的常数项，可以省略；a1、a2、a3、a4为需要拟合解的数。

(5)

式中：Δ为突变特征值；w、v为控制变量。

突变特征值Δ的大小可以作为岩体演化状态与临界状态的判断依据。当根据内嵌的FISH函数计算测点位移的突变特征值[13-15]小于零时，认为围岩由稳定转为失稳达到塑性破坏状态，此时所得的位移值为该条件下的极限位移值；如果任意测点的特征值始终大于或等于零，则认为在此种岩土及支护参数条件下隧道开挖结束后，围岩始终处于稳定状态，选取最大不平衡率小于1×10-5时的位移值作为相应的极限位移值，因为此时围岩体系的外力与内力的比值已相当小，体系达到力的平衡，位移处于极限收敛状态，位移曲线趋于稳定。通过统计分析交叉计算的结果，得出监控断面在不同条件下，不同测点受上下台阶开挖影响的位移值，以及最终的极限位移值。

考虑到模拟结果数值的边沿性，即模拟计算得到最大、最小值可能会对相对位移值的范围统计产生影响。根据3σ法则，极限位移近似假设为正态分布，那么68%的数值分布在距离均值1个标准差的范围内，约95%的数值分布在距离均值2个标准差的范围内，约99.7%的数值分布在距离均值3个标准差的范围内。因此，按数理统计原理可选择E±2σ的值作为统计数列的最大、最小值，这样的取值相较于模拟计算出来的最大值、最小值更为合理。以Ⅲ级围岩为例，列出围岩初期支护极限相对位移统计表，如表5所示；以及各级围岩不同位置处相对位移平均值与埋深关系如图5所示。

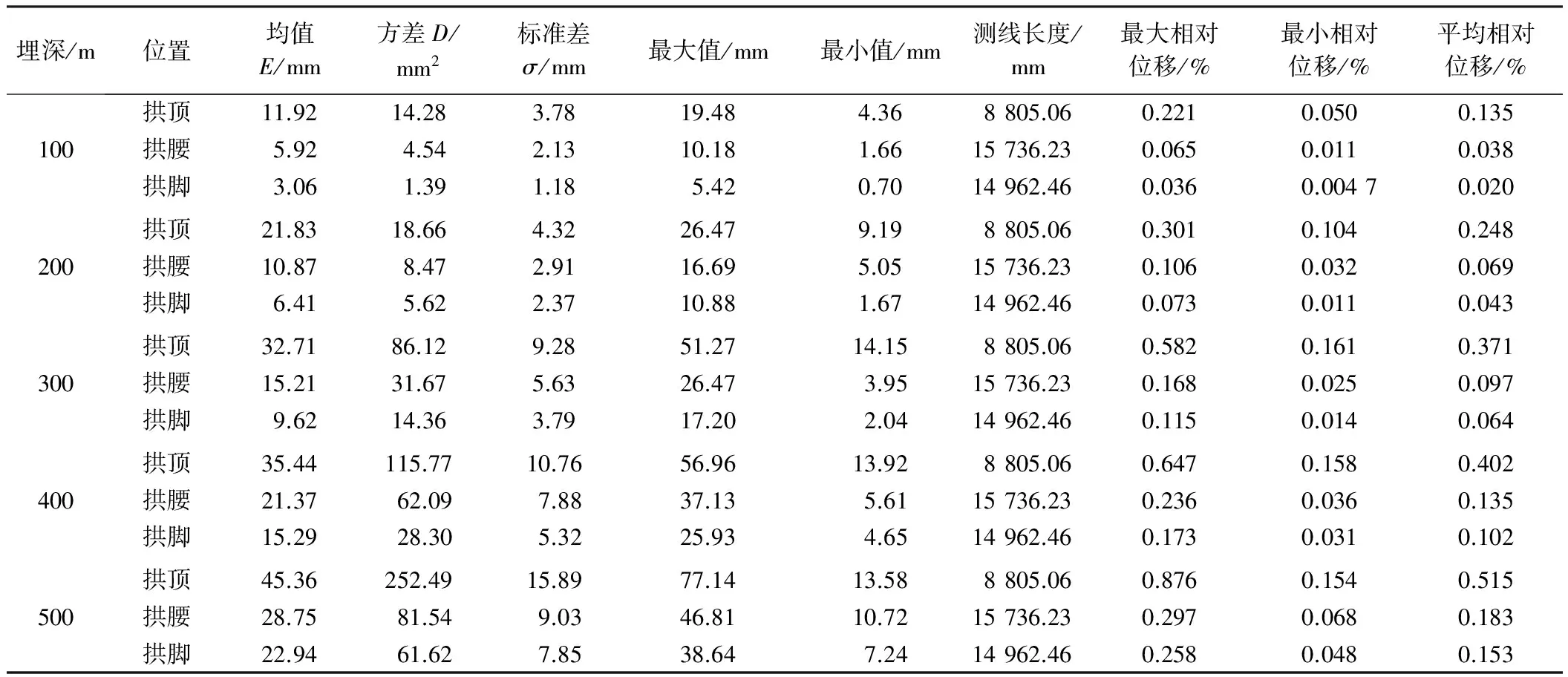
表5 Ⅲ级围岩3车道隧道初期支护极限相对位移统计表

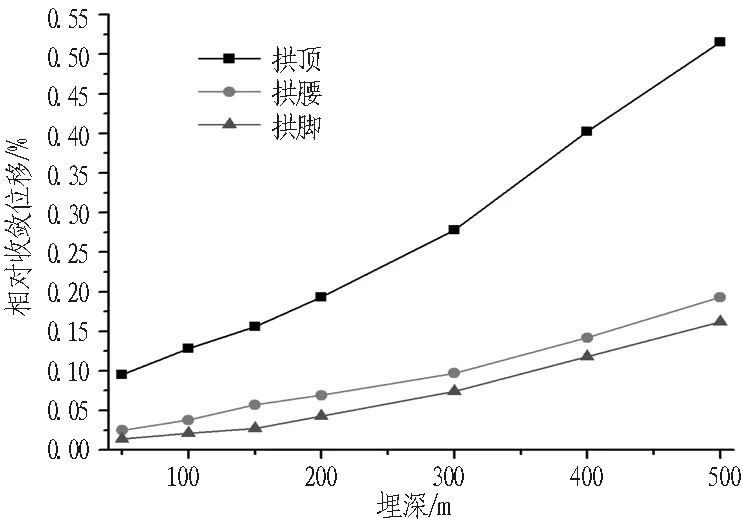
(a) Ⅲ级围岩

(b) Ⅳ级围岩

Fig. 5 Relationship between average relative displacement and buried depth of different positions in different grades of surrounding rocks

通过对图5进行分析，表明不同围岩级别下，初期支护各位置处的极限相对位移值的整体分布趋势基相同，各位置的相对位移值随围岩级别的增大(Ⅲ—Ⅴ)而升高，随隧道埋深的增加而增大。相对位移的变化速率基本上呈现由小到大非线性的变化趋势，并且当埋深超过200 m时，变形增加的幅度相对突出，以Ⅲ级围岩拱顶为例，每100 m相对位移随埋深增长的比率为0.065 (100～200 m)、0.084 (200～300 m)、 0.124 (300～400 m)、0.173 (400～500 m)，300 m以后增长速率明显增加。围岩条件越差，相同埋深区段，相同位置的变形增长越快。以拱顶为例，在埋深为500 m时，Ⅲ级围岩沉降值为45.36 mm，Ⅳ级围岩为63.52 mm，而Ⅴ级围岩的沉降值已增至104.3 mm,增幅变化明显。

根据对各级围岩初期支护极限相对位移的对比，发现隧道断面在相同埋深区段中不同位置的相对收敛位移值(变形值与变形后测线长度的比值)相差明显，基本上拱顶处的相对沉降值大于其他测点的相对收敛值。排除不同点位测线长度的差异(拱顶的测线长度远小于拱腰、拱脚)，拱顶、拱腰、拱脚的位移值随着埋深的变化，三者之间的数值差距也明显不同。Ⅲ级围岩时，拱顶的沉降值远大于拱腰和拱脚处的收敛值，埋深为500 m时，拱顶为45.36 mm,而最小的拱脚只有22.94 mm；Ⅳ级围岩条件下，拱脚处的变形较大，当埋深为300 m时，拱脚的变形值为58.16 mm，拱顶为37.45 mm，二者相差20.71 mm，而当埋深为500 m时，拱脚的变形值100.28 mm,拱顶只有63.52 mm，相差36.76 mm，二者的变形值相差明显；在Ⅴ级围岩中，拱腰的变形值又远大于其他位置，埋深为300 m时，拱腰的变形值是86.82 mm，拱顶为76.44 mm,差距只有10.38 mm,但当埋深取为500 m时，拱脚变形值增至134.46 mm,拱顶为104.3 mm，二者之间的差距陡增为30.16 mm。可见不同围岩级别，不同测点的变形表现各不相同，并且随着埋深的增加，相差的数值愈发显著。同时，隧道各测点的变形还要受到空间效应的影响，即不同的开挖区域对不同测点变形量的影响也不同。拱顶、拱腰和拱脚受上、下台阶开挖影响所占的变形比例如表6所示。

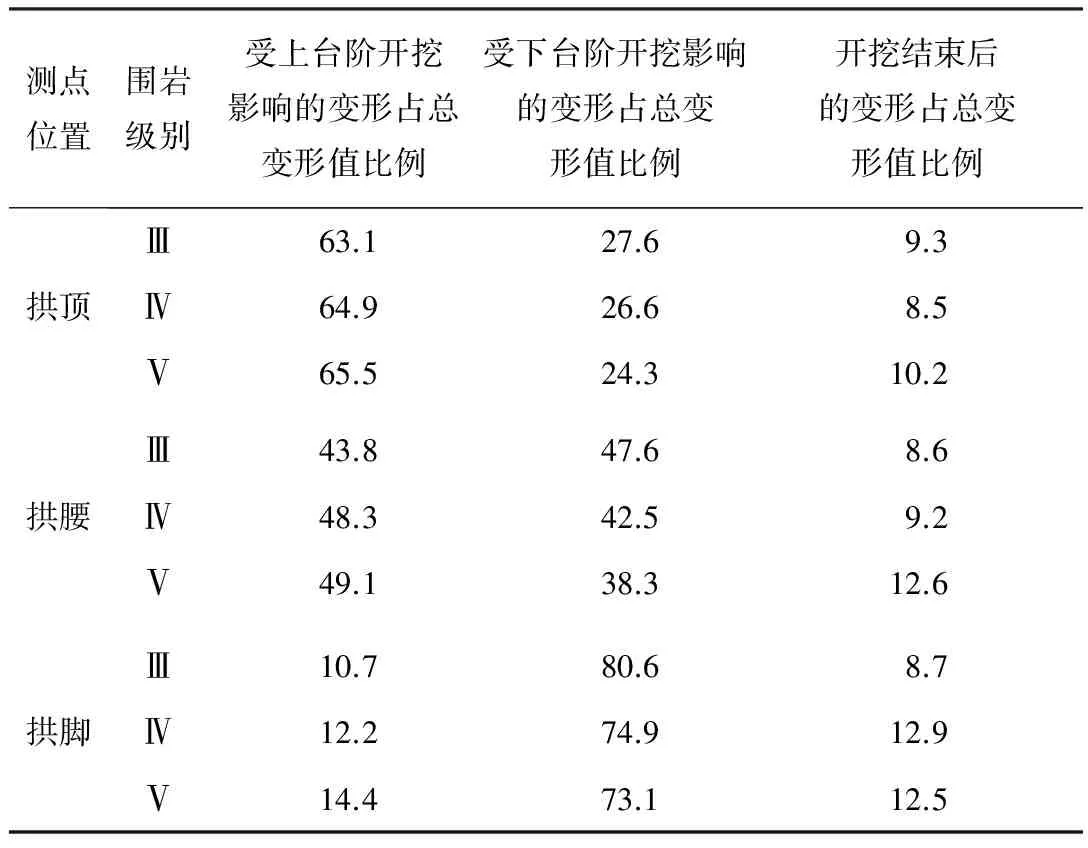
表6 各围岩级别下断面不同位置受上下台阶开挖影响的变形比例

注： 1)表中所给的不同位置处不同围岩级别，上、下台阶开挖的比例值为模拟得到的所有埋深条件下所对应的比例均值; 2)总变形值为监控断面不同位置处，在不同埋深和围岩级别下达到极限条件时的最终位移值。

依据对表6统计数字的分析和计算，可见上台阶开挖支护后，拱顶处的变形明显，随着围岩条件的恶化，上台阶所占比例略有增加，分别占最终变形值的63.1%、64.9%、65.5%，而且随着埋深的增加，上台阶所占比例也会相应增加；由于拱腰处于上、下台阶的交界处，因此上、下部的开挖对其的影响基本一致，分别约占47%和43%；拱脚距离上台阶开挖支护的临空面较远，因而受到的位移变化影响较小，约占最终变形值的12%。不同测点位置，随着围岩条件的恶化，上台阶开挖的变形值所占比例基本呈现略微增大的趋势。监控断面不同点位，在隧道全部开挖支护后的变形值只占最终极限值的10%左右，可见及时有效的支护手段可以减小支护体系的变形发展趋势。

4 结论与建议

根据对本文模拟结果与规范所给数据的对比分析，得出如下结论：

1)考虑到不同埋深下，不同测点极限相对位移值差异明显，因此可将规范中“洞周”细化为拱顶、拱腰、拱脚等具有代表性的位置，不同位置应有不同的允许极限范围值。

2) 规范中埋深只分了3个档次，而且由于后2档所包含的范围太过粗略，同一档内的差异不能充分体现出来。根据对模拟结果的分析，在每个埋深档次内埋深越大，极限相对位移值的非线性关系越明显，不能简单的通过线性内插计算。因此可将埋深范围细化，方便不同条件的隧道工程施工操作。

3) 针对3车道断面形状，根据不同的围岩级别，应侧重不同点位的量取，并依据监控量测的变形值及稳定程度，为修改初期支护方案，指导施工作业以保证隧道的稳定性提供依据。初期支护的极限位移，可以作为二次衬砌施作时机选取的标准。

交叉模拟各位置处的极限相对位移值虽然均在规范给定的范围值之内，但存在计算模型和计算参数的限制，与实际情况在一定程度上还是存在差异。采用极限位移判别隧道稳定性，应详细考虑各种因素对位移值的影响，目前对初期支护完全破坏的条件还较难界定，本文采用位移值的突变理论来判断极限状态，这一理论还有待进一步的深入研究，同时本文只研究了台阶开挖的影响。随着地下工程与岩体力学研究的不断发展，今后可在考虑各种地质条件下，对不同类型的隧道，在不同开挖方式下相应的允许相对位移值进行研究，并进一步完善极限状态的判别理论，从而为实际工程施工提供更加详细的规范参考。

[1] 张长亮, 王晓雯, 陈华. 隧道围岩变形预测预报方法研究 [J]. 公路交通科技, 2008(4): 88. ZHANG Changliang, WANG Xiaowen, CHEN Hua. Study of forecast and prediction methods for tunnel wall rock deformation[J]. Technology of Highway and Transport, 2008(4): 88.

[2] 崔宏伟, 李德武. 滑坡地段浅埋隧道极限位移研究及围岩稳定性评价[J]. 兰州交通大学学报, 2011, 30(3): 5. CUI Hongwei, LI Dewu. The limit displacement of shallow tunnel in landslide area and the stability evaluation of surrounding rock[J]. Journal of Lanzhou Jiaotong University, 2011, 30(3): 5.

[3] 朱永全, 张素敏, 景诗庭. 铁路隧道初期支护极限位移的确定及意义 [J]. 岩石力学与工程学报, 2005, 24(9): 1594. ZHU Yongquan, ZHANG Sumin, JING Shiting. Concept and determination of limit displacements of primary support system of railway tunnel[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(9): 1594.

[4] 朱永全, 景诗庭, 赵玉成. 大变形隧道极限位移的计算模拟 [J]. 石家庄铁道学院学报, 2000, 13(3): 75. ZHU Yongquan, JING Shiting, ZHAO Yucheng. The imitation calculation of limit displacements for large deformation tunnelling [J]. Journal of Shijiazhuang Railway Institute, 2000, 13(3): 75.

[5] 招商局重庆交通科研设计有限公司. 公路隧道设计规范： JTG D70—2014 [S]. 北京: 人民交通出版社, 2014. China Merchants Chongqing traffic research & Design Co., Ltd. Specification for Design of Highway Tunnels：JTG D70—2014 [S]. Beijing: China Communication Press, 2014.

[6] 鞠天祥. 新奥法施工技术在公路隧道工程中的应用 [J]. 桥梁与隧道工程， 2014(4): 60. JU Tianxiang. Application of NATM in highway tunnel engineering[J]. Bridge and Tunnel Engineering, 2014(4): 60.

[7] 陈秋南. 隧道工程 [M]. 北京: 机械工业出版社, 2007. CHEN Qiunan. Tunnel engineering[M]. Beijing: China Machine Press, 2007.

[8] 中交第二公路勘察设计研究院. 公路隧道设计细则： JTG/T D70—2010 [S].北京: 人民交通出版社, 2010. China Communication Second Highway Consultant Co.， Ltd. Guidelines for design of highway tunnel： JTG/T D70—2010[S].Beijing: China Communication Press, 2010.

[9] HOEK E, BROWN E T. Practical estimates of rock mass strength [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165.

[10] 王可意, 徐东强. 定量化GSI在估计岩体力学参数中的应用研究[J]. 铁道科学与工程学报， 2016, 13(11): 2168. WANG Keyi, XU Dongqiang. Application of quantitative GSI in the estimation of rock mechanics parameters[J]. Journal of Railway Science and Engineering, 2016, 13(11): 2168.

[11] 苏永华, 封立志, 李志勇, 等. Hoek-Brown准则中确定地质强度指标因素的量化 [J]. 岩石力学与工程学报, 2009, 28(4): 679. SU Yonghua, FENG Lizhi, LI Zhiyong， et al. Quantification of elements for geological strength index in Hoek-Brown criterion [J].Chinese Journal of Rock Mechanics and Engineering, 2009, 28(4): 679.

[12] 朱合华, 张琦, 章连洋. Hoek-Brown强度准则研究进展与应用综述[J].岩石力学与工程学报, 2013, 32(10): 1945. ZHU Hehua, ZHANG Qi, ZHANG Lianyang. Review of research progresses and applications of Hoek-Brown strength criterion [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(10): 1945.

[13] 赵延林, 吴启红, 王卫军, 等. 基于突变理论的采空区重叠顶板稳定性强度折算法及应用[J].岩石力学与工程学报, 2010, 29(7): 1424. ZHAO Yanlin, WU Qihong, WANG Wenjun， et al. Strength reduction method to study stability of goaf overlapping roof based on catastrophe theory [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(7): 1424.

[14] 赵志峰, 徐卫亚. 基于突变理论的边坡安全稳定性综合评价[J]. 岩石力学与工程学报, 2007, 26(增刊1): 2707. ZHAO Zhifeng, XU Weiya. Comprehensive assessment of slope safety and stability based on catastrophe theory[J].Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S1): 2707.

[15] 马莎, 肖明. 基于突变理论和监测位移的地下洞室稳定评价方法[J]. 岩石力学与工程学报， 2010, 29(增刊2): 3812. MA Sha, XIAO Ming. Judgment method for stability of underground cavern based on catastrophe theory and monitoring displacement [J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2): 3812.

DeterminationofUltimateRelativeDisplacementsofPrimarySupportofMountain-crossingHighwayTunnel

XU Dongqiang, YAN Peng*, LI Yanqi, WANG Keyi

(SchoolofCivilEngineeringandTransportation,HebeiUniversityofTechnology,Tianjin300401,China)

U 451

A

1672-741X(2017)09-1083-07

2017-01-09;

2017-03-28

河北省交通运输厅2013年度科研项目 (201302025)

徐东强(1958—)，男，河北藁城人，2002年毕业于中国矿业大学，土木工程专业，博士，教授，主要从事岩体工程、隧道与地下工程等方面的研究工作。E-mail: xudq58@163.com。 *通信作者： 燕鹏， E-mail: ypzb2008@163.com。

10.3973/j.issn.1672-741X.2017.09.004