稳定渗流条件下挡土结构水、土压力分布探讨

李晓玮，刘翠娜

（1. 北京市地质研究所，北京100120；2. 科学出版社，北京 100717）

稳定渗流条件下挡土结构水、土压力分布探讨

李晓玮1，刘翠娜2

（1. 北京市地质研究所，北京100120；2. 科学出版社，北京 100717）

在暴雨造成地下水位比较浅的情况下，由于墙前后水头差引起的渗流常常使挡土结构发生破坏。本文选取了稳定渗流条件下，分别采用土-水整体作为隔离体以及土骨架作为隔离体进行分析，归纳总结了不同水位以及不同类型的土体土、水压力计算，进而探讨挡土结构两侧土、水压力分布规律。当墙前后以及基底土为均质的粘性土时，对于板桩等悬臂式挡土结构，由于底部宽度远小于长度，故可将底部段造成的水头损失忽略。此时，当水头差足够大，渗流作用造成土体发生流土时，板桩一侧向上渗流范围内对挡土结构无被动土压力，另一侧向下渗流范围内对挡土结构的主动土压力增大为静水工况时主动土压力的2倍。当墙前地下水位平基底，基底为透水地基，墙后为均质粘性土时，挡土构件侧面、底部所受的水压力均为0。

稳定渗流；挡土结构；土压力；水压力

0 前言

在边坡和基坑工程中，各种挡土结构的稳定性是保证工程安全的前提，稳定性计算通常采用朗肯和库伦土压力理论，其中朗肯理论是由一点的极限平衡出发，求出应力及其分布，进而计算土压力合力。库伦理论是根据墙背与滑动面之间的土楔整体极限平衡状态，首先求出土压力合力，需要时再计算应力及分布（李广信等，2013）。对于墙背光滑垂直、填土水平的情况使用朗肯理论较为方便。本文即采用朗肯理论进行土压力计算。

在有静水位的情况，由于增加了静水压力使得挡土结构上的作用力发生了变化，并且静水压力常常不利于挡土结构的稳定。尤其在暴雨造成地下水位比较浅工况下，由于墙前后水头差引起的渗流使得挡土结构的水土压力计算更为复杂，更容易使挡土结构发生破坏。向下的渗透力增加了主动土压力，向上渗透力减少了被动土压力，所以实际失事的情况可能是：墙体由于被动侧抗力不够而倾覆（李广信，2010）。本文选取了稳定渗流条件下，分别采用土-水整体作为隔离体以及土骨架作为隔离体进行分析，运用水土分算方法，归纳总结了不同水位以及不同类型的土体土、水压力计算，进而探讨挡土结构两侧土水压力分布规律。

1 计算方法

在考虑渗流作用，分析土体受力平衡或者稳定性时，可以有两种取隔离体的方法：一是考虑土-水整体作为隔离体，此时应用土体饱和重度与作用于土体周边边界上的水压力相组合；二是把土骨架当做隔离体，用土体的浮重度γ′与渗透力j相组合（李广信等，2013）。

土-水整体作为隔离体是对土骨架和孔隙水整体进行受力分析，整体受到重力，以及向上的水压力。首先计算整体竖向总压力，在计算孔隙水压力，进而计算出土体竖向有效应力，再乘以水平土压力系数求出水平土压力。

土骨架作为隔离体是对土骨架进行受力分析，土骨架受到浮力γ′以及水通过土间隙形成的渗透力j。直接求出土体竖向有效应力，再乘以水平土压力系数求出水平土压力。需要时再根据水头高度求出孔隙水压力。

2 计算模型1

重力式挡土墙，墙前后以及基底土为均质粘性土。墙前（左侧）地下水位与d点同高，墙后（右侧）地下水位与墙顶a同高（图1）。ΔH为总水头损失，Δh1为cd段总水头损失，Δh2为ab段总水头损失，Δh3为bc段总水头损失。则

总水头损失：

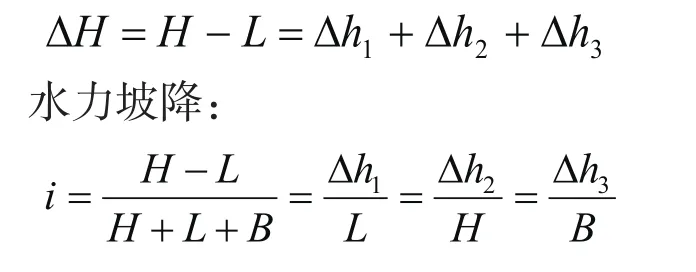
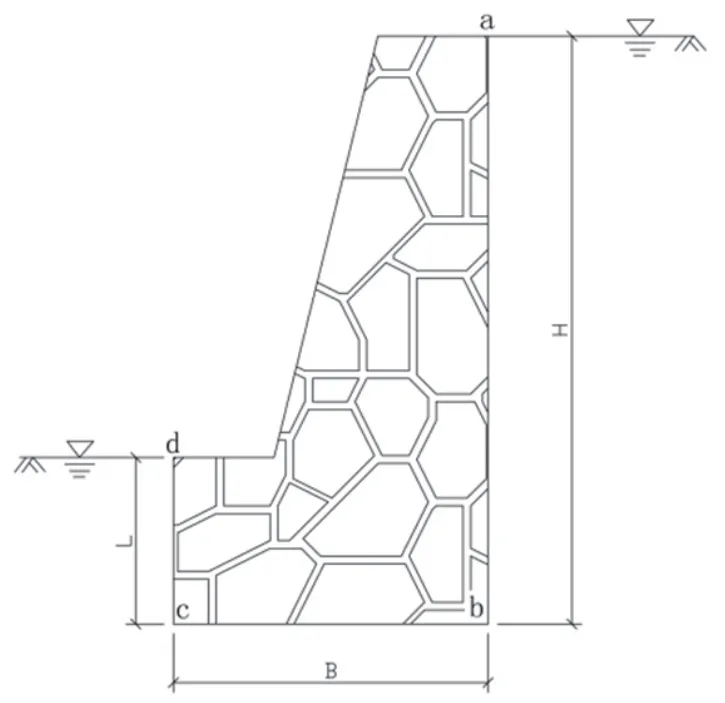
图1 计算模型1Fig.1 Computational model 1

2.1 土-水整体作为隔离体

对土骨架和孔隙水整体进行受力分析，整体受到重力，以及向上的水压力。

（1）左侧土体对挡墙作用力分析

挡墙左侧土体竖向总应力计算：

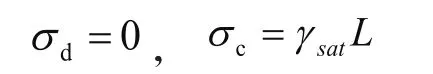
挡墙左侧孔隙水压力计算：

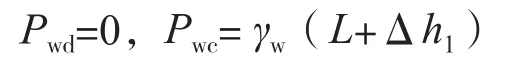
挡墙左侧土体竖向有效应力计算：

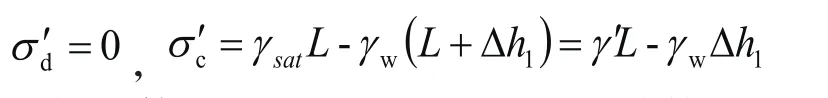
左侧土体对挡土结构被动土压力计算：

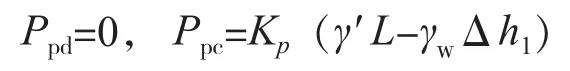
其中：Ka=tan2（45+φ/2）

（2）右侧土体对挡墙作用力分析

挡墙右侧土体竖向总应力计算：

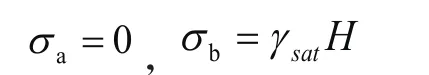
挡墙右侧孔隙水压力计算：

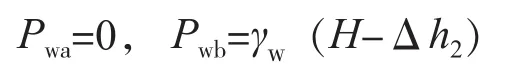
挡墙右侧土体竖向有效应力计算：

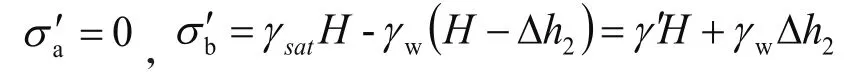
右侧土体对挡土结构主动土压力计算：

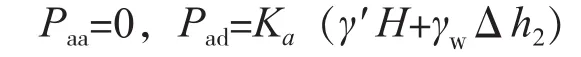
其中：Ka=tan2（45-φ/2）

2.2 土骨架作为隔离体

对土骨架进行受力分析，土骨架受到浮力γ′以及水通过土间隙形成的渗透力j。

（1）左侧土体受到向上的渗流作用

左侧土体竖向有效应力计算：

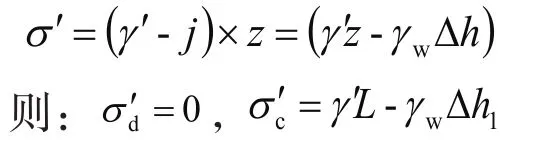
左侧土体对挡土结构被动土压力计算：

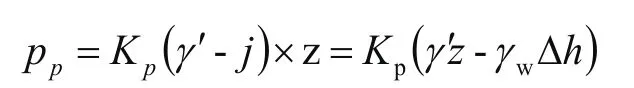
则：Ppd=0，Ppc=Kp（γ′L-γwΔh1）

左侧孔隙水压力计算：

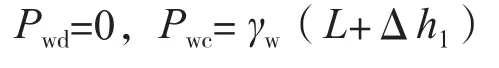
（2）右侧土体受到向下的渗流作用

右侧土体竖向有效应力计算：

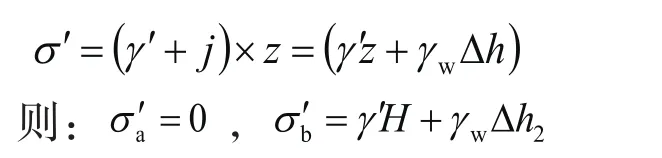
右侧土体对挡土结构主动土压力计算：

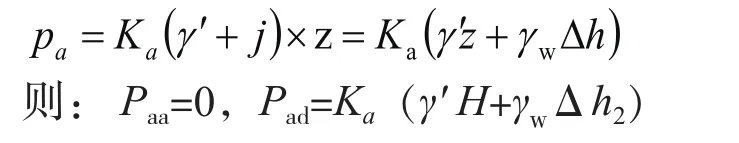
右侧孔隙水压力计算：

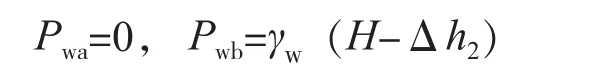
可知两种方法计算结果一致。挡墙两侧水压力、土压力分布见图2，基底水压力分布见图3。

3 计算模型2

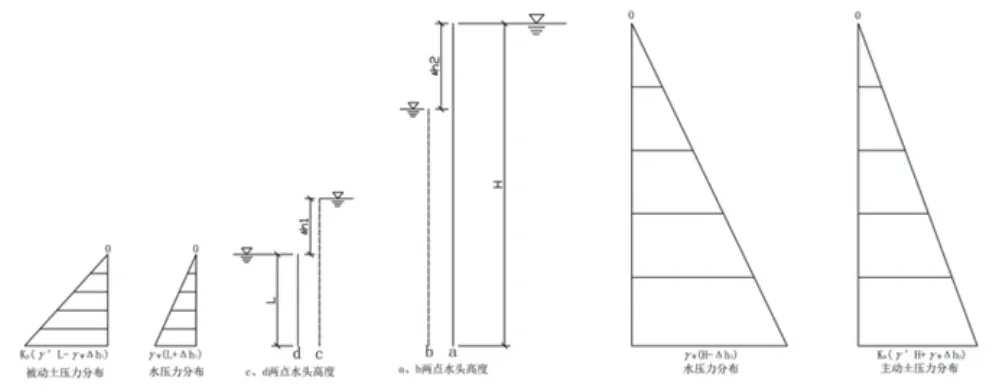
图2 挡墙两侧水、土压力分布Fig.2 Distribution of water and earth pressure on retaining wall

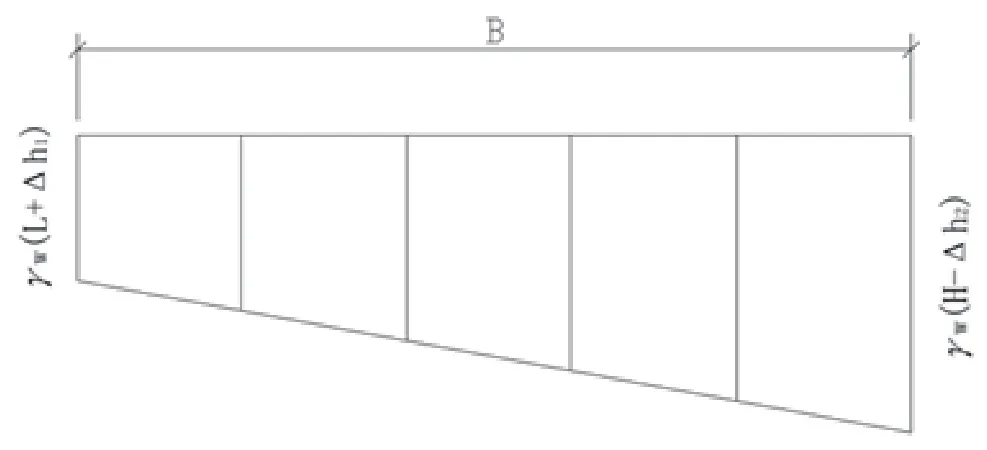
图3 基底水压力分布Fig.3 Base water pressure distribution

板桩挡土结构前后以及基底土为均质粘性土（松岗元，2001）。墙前（左侧）地下水位与d点同高，墙后（右侧）地下水位与桩顶a同高（图4）。ΔH为总水头损失，Δh1为cd段总水头损失，Δh2为ab段总水头损失。当采用板桩等悬臂式挡土结构时，由于底部bc段宽度远小于H，将底部bc段造成的水头损失Δh3忽略，即b、c两点水头高度相等

总水头损失：

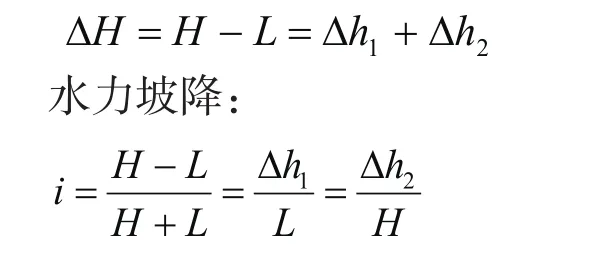
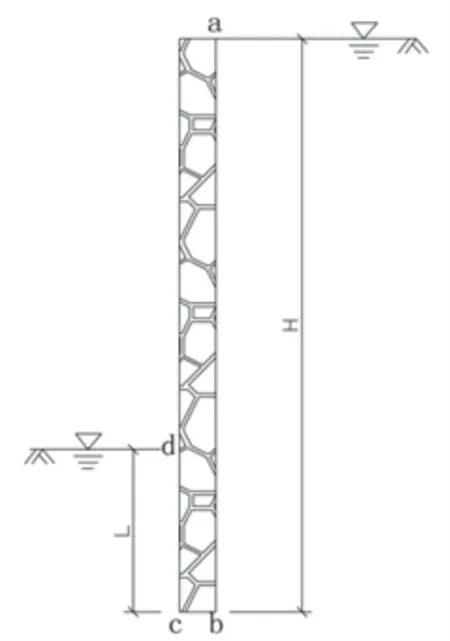
图4 计算模型2Fig.4 Computational model 2

用土骨架作为隔离体的方法计算墙前后水、土压力：

对土骨架进行受力分析，土骨架受到浮力γ′以及水流动对土的渗透力j。根据2. 2所得的结论：

左侧土体对挡土结构被动土压力计算：

Ppd=0，Ppc=Kp（γ′L-γwΔh1）

左侧孔隙水压力计算：

Pwd=0，Pwc=γw（L+Δh1），

右侧土体对挡土结构主动土压力计算：

Paa=0，Pad=Ka（γ′H+γwΔh2） ，

右侧孔隙水压力计算：

Pwa=0，Pwb=γw（H-Δh2），

板桩两侧水压力、土压力分布见图5。当渗流力足够大，渗流作用造成土体发生流土时，即：

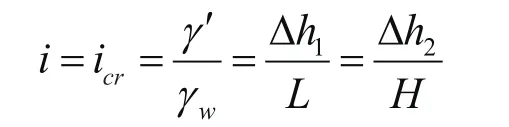
此时：

Ppc=Kp（γ′L-γwΔh1）=0，即渗流范围内左侧土体对挡土结构无被动土压力。

Pad=Ka（γ′H+γwΔh2）=2Kaγ′H，即渗流范围内右侧土体对挡土结构的主动土压力增大为静水工况时主动土压力的2倍。

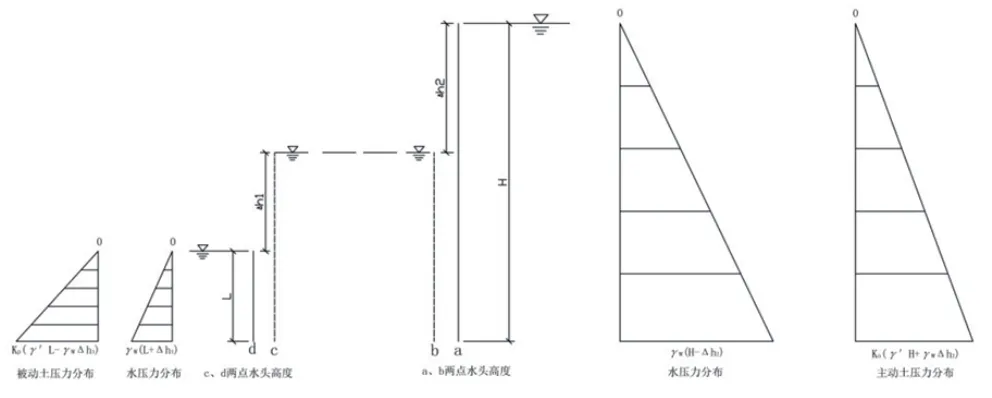
图5 板桩两侧水、土压力分布Fig.5 Distribution of water and soil pressure on both sides of piles

4 计算模型3

重力式挡土墙，基底为透水地基，墙后为均质粘性土（高大钊，2010）。墙前（左侧）地下水位与基底c同高，墙后（右侧）地下水位位于m点（图6）。ΔH为总水头损失，Δh2为md段水头损失。

总水头损失：

ΔH=Δh2=H2

mb段水力坡降：

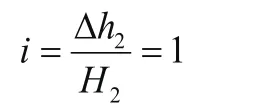
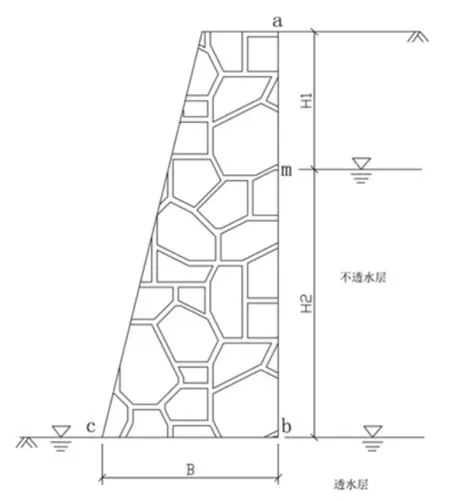
图6 计算模型3Fig.6 Computational model 3

4.1 土-水整体作为隔离体

竖向总应力计算：

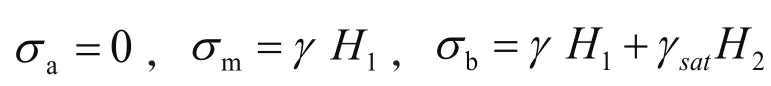
孔隙水压力计算：

Pwa=0，Pwd=0

竖向有效应力计算：

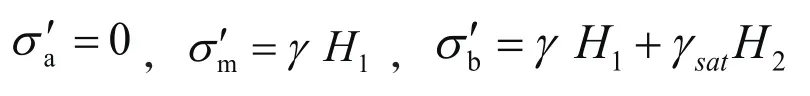
主动土压力计算：

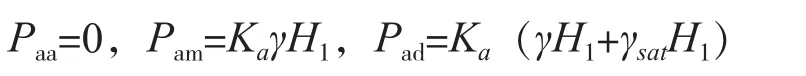
4.2 土骨架作为隔离体

ΔH2为总水头损失，水力坡降：土体竖向有效应力：

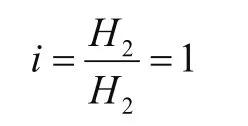
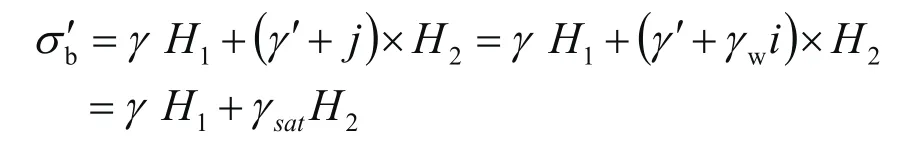
土体对支挡结构主动土压力：Paa=0，Pad=Ka（γH1+γsatH2）

孔隙水压力：

Pwa=0，Pwd=0

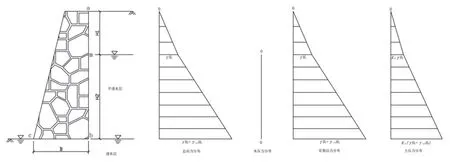
图7 挡墙右侧水、土压力分布Fig.7 Distribution of water and earth pressure on the right of retaining wall

5 结论

本文利用朗肯理论分别用土-水整体作为隔离体以及土骨架作为隔离体分析计算稳定渗流条件下挡土结构所受水、土压力。可知该条件下以土骨架作为隔离体计算方法较为方便。

当发生稳定渗流时，与静水位相比，挡土结构水头高的一侧发生向下渗流，增大了土压力，减小了水压力；水头低的一侧发生向上渗流，减小了土压力，增大了水压力。

当墙前后以及基底土为均质的粘性土时，对于板桩等悬臂式挡土结构，由于底部宽度远小于长度，故可将底部段造成的水头损失忽略。此时，当水头差足够大，渗流作用造成土体发生流土时，板桩一侧向上渗流范围内对挡土结构无被动土压力，另一侧向下渗流范围内对挡土结构的主动土压力增大为静水工况时主动土压力的两倍。

当墙前地下水位平基底，基底为透水地基，墙后为均质粘性土时，挡土构件侧面、底部所受的水压力均为零。

李广信，张丙印，于玉贞，2013. 土力学[M]. 北京：清华大学出版社，68-71，89-91.

李广信，2010. 岩土工程50讲—岩坛漫话（第二版）[M]. 北京：人民交通出版社.

松岗元，2001. 土力学[M]. 北京：中国水利水电出版社.

高大钊，2010. 岩土工程勘察与设计—岩土工程疑难问题答疑笔记整理之二[M]. 北京：人民交通出版社.

中华人民共和国住房和城乡建设部，2012. 建筑基坑支护技术规程（JGJ 120-2012）[S].

中华人民共和国住房和城乡建设部，2013. 建筑边坡工程技术规范（GB 50330-2013）[S].

The Study on the Distribution of Water and Soil Pressure on Retaining Structure under Steady Seepage Condition

LI Xiaowei1, LIU Cuina2

(1.Beijing Institute of Geology, Beijing 100120; 2. China Science Publishing & Media Lab, Beijing 100717)

The seepage of the retaining wall due to the difference between the front and the back of the wall often causes the failure of the retaining structure, especially in the case of shallow water caused by heavy rainfall.Under the steady fl ow condition, this paper takes the soil-water as a whole body and isolated soil skeleton as an isolator, and summarizes the calculation of different level and different soil and water pressure, and then discusses the retaining structure on both sides of the soil, water pressure distribution. When the soil around the wall and the foundation soil are homogeneous and cohesive soil, the soil loss due to the bottom of the cantilever retaining structure is much smaller than that of the length of the retaining wall. At this time, when the water head difference is large enough, the seepage caused by soil body fl ow will occur when the pile side upward seepage in the range of retaining structure of passive earth pressure, 2 times of active earth pressure on retaining structure for increasing hydrostatic condition of active earth pressure on the other side of the downward fl ow range. When the water level in front of the wall is fl at, the basement will be pervious to water, and the water pressure on the side and bottom of the retaining member is zero.

Steady seepage; Retaining structure; Earth pressure; Water pressure

A

1007-1903（2017）03-0036-05

10.3969/j.issn.1007-1903.2017.03.007

李晓玮（1985- ），男，硕士，工程师，主要从事地质灾害防治等方面研究。E-mail:51350737@qq.com